河南省漯河市舞阳县2021届九年级上学期期末考试数学试题 10页

2020—2021 学年上学期期末考试试卷 九年级数学 注意事项：本试卷共 8 页，三大题，满分 120 分，考试时间 100 分钟.闭卷考试，请将答案直接写在 试卷或答题卡上. 一、选择题（每小题 3 分，共 30 分）下列各小题均有四个答案，其中只有一个是正确的，将正确答 案的代号字母填入题后括号内. 1．下列说法中错误的是 （ ） A．不可能事件发生的概率为 0 B．概率很小的事不可能发生 C．必然事件发生的概率是 1 D．随机事件发生的概率大于 0、小于 1 2．已知⊙O 的直径为 12cm，如果圆心 O 到一条直线的距离为 7cm，那么这条直线与这个圆的位置关 系是 （ ） A． 相离 B． 相切 C． 相交 D． 相交或相切 3．下列四个圆形图案中，分别以它们所在圆的圆心为旋转中心，顺时针旋转 120°后，能与原图形 完全重合的是 （ ） A． B． C． D． 4．如图，在⊙O中，∠ABC＝50°，则∠AOC等于 （ ） A．50° B．80° C．90° D．100° 5.不透明袋子中装有红、绿小球各一个，除颜色外无其他差别，随机摸出一个小球后，放回并 摇匀，再随机摸出一个，两次都摸到红球的概率为 （ ） A. B. C. D. 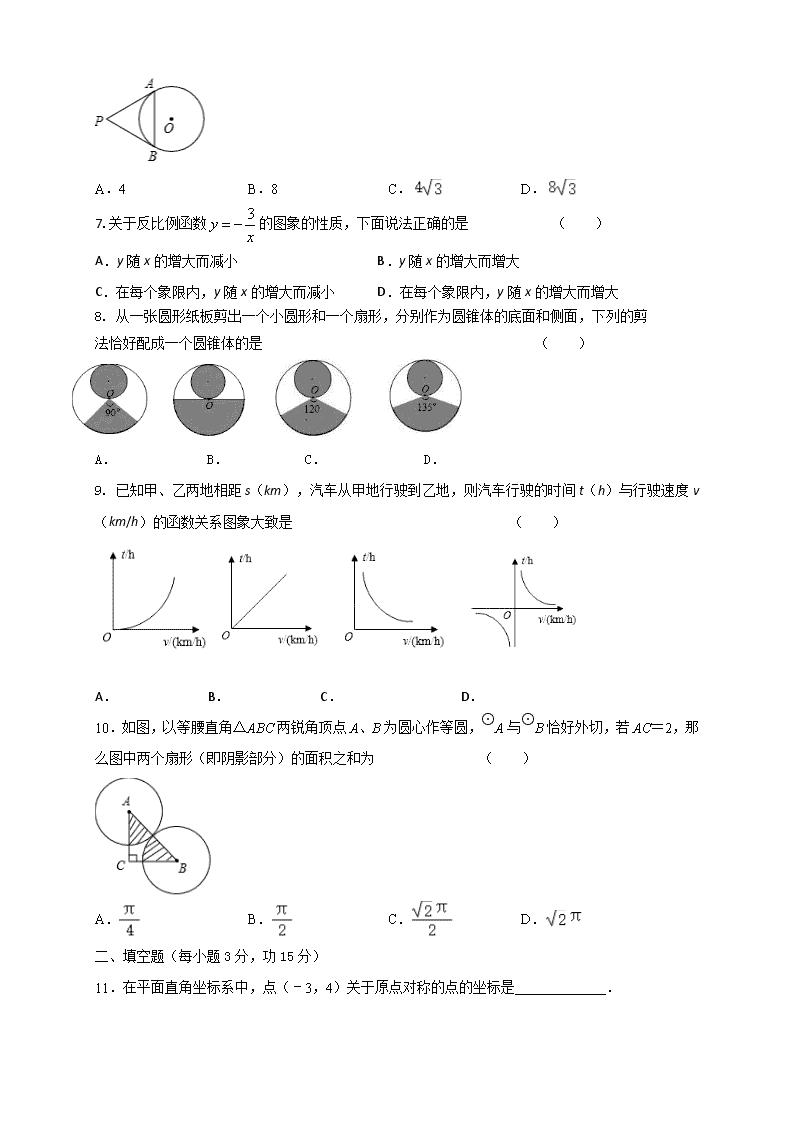6．如图，从圆 O外一点 P引圆 O的两条切线 PA，PB，切点分别为 A，B．如果∠APB＝60°，PA ＝8，那么弦 AB的长是 （ ） A．4 B．8 C． D． 7.关于反比例函数 x y 3  的图象的性质，下面说法正确的是 （ ） A．y 随 x 的增大而减小 B．y 随 x的增大而增大 C．在每个象限内，y 随 x 的增大而减小 D．在每个象限内，y 随 x 的增大而增大 8. 从一张圆形纸板剪出一个小圆形和一个扇形，分别作为圆锥体的底面和侧面，下列的剪 法恰好配成一个圆锥体的是 （ ） A． B． C． D． 9. 已知甲、乙两地相距 s（km），汽车从甲地行驶到乙地，则汽车行驶的时间 t（h）与行驶速度 v （km/h）的函数关系图象大致是 （ ） A． B． C． D． 10．如图，以等腰直角△ABC两锐角顶点 A、B为圆心作等圆，⊙A与⊙B恰好外切，若 AC＝2，那 么图中两个扇形（即阴影部分）的面积之和为 （ ） A． B． C． D． 二、填空题（每小题 3 分，功 15 分） 11．在平面直角坐标系中，点（﹣3，4）关于原点对称的点的坐标是 ． 12．在一个不透明的布袋中装有 2个白球和 n个黄球，它们除颜色不同外，其余均相同．若从中随 机摸出一个球，它是黄球的概率是 ，则 n＝ ． 13．已知圆锥的底面圆半径为 3cm、高为 4cm，则圆锥的侧面积是 cm2． 14．如图，PA、PB是⊙O的切线，A、B为切点，点 C、D在⊙O上．若∠P＝108°，则∠B+∠D ＝ ． 15．如图，∠ABC＝90°，O为射线 BC上一点，以点 O为圆心、 BO长为半径作⊙O，当射线 BA 绕点 B按顺时针方向旋转 度时与⊙O相切． 三、解答题（共 8 小题，满分 75 分） 16．（8分）解方程： （1）x2﹣4x﹣1＝0 （2）2（x﹣1）2﹣16＝0． 17．（7分）把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知 EF=CD=16cm， 请求出球的半径。 18．（9 分）从 1 名男生和 3 名女生中随机抽取参加“我爱祖国”演讲比赛的同学． （1）若抽取 1 名，恰好是男生的概率为 ； （2）若抽取 2 名，求恰好是 2 名女生的概率（用树状图或列表法求解）． 19. （10分）如图，在△ABC中，AB=BC，以 AB为直径的⊙O交 AC于点 D，DE⊥BC，垂足为 E． （1）求证：DE是⊙O的切线；（2）若 DG⊥AB，垂足为点 F，交⊙O于点 G，∠A=35°，⊙O半 径为 5，求劣弧 DG的长（结果保留π）． 20. （10分）如图，已知反比例函数 y= （m为常数）的图象经过□ABOD的顶点 D，点 A、B 的坐标分别为（0，3），（﹣2，0）（1）求出 m的值及函数解析式；（2）设点 P是该反比例函数 图象上的一点，若 OD=OP，求 P点的坐标． 21．（10 分）某学习小组在学习了函数及函数图象的知识后，想利用此知识来探究周长一定时，矩 形的面积与边长函数关系式的图象．请将他们的探究过程补充完整． （1）列函数表达式：若矩形的周长为 8，设矩形的一边长为 x，面积为 y，则有 y＝ ； （2）上述函数表达式中，自变量 x 的取值范围是 ； （3）列表： x … 0.5 1 1.5 2 2.5 3 3.5 … y … 1.75 3 3.75 4 3.75 3 m … 写出 m＝ ； （4）画图：在平面直角坐标系中已描出了上表中部分各对应值为坐标的点，请你画出该函数的图象． 22．（10分）某学生利用暑假 40 天进行社会实践，参与了一家网店的经营，了解到一种成本为 20 元/件的商品在 x 天销售的相关信息如表所示． 销售量 P（件） P=50-x 销售单价 m（元/件） 当 1≤x≤20 时， xm 2 130  当 21≤x≤40 时， x m 52520  （1） 请计算第几天该商品的销售单价为 35 元/件？ （2） 设该网店第 x 天获得的利润为 y，求出 y与 x的函数关系式。 （3）这 40 天中该网店第几天获得的利润最大？最大的利润是多少？ 23．（11 分）如图，二次函数 y＝ x2+bx+c 的图象交 x 轴于 A、D 两点，并经过 B 点，已知 A 点坐 标是（2，0），B 点坐标是（8，6）． （1）求二次函数的解析式； （2）求函数图象的顶点坐标及 D 点的坐标； （3）二次函数的对称轴上是否存在一点 C，使得△CBD 的周长最小？若 C 点存在，求出 C 点的坐标； 若 C 点不存在，请说明理由． 2020-2021 学年（上）学期期末考试 九年级数学参考答案及评分标准 说明： 1.如果考生的解答与本参考答案提供的解法不同，可根据提供的解法的评分标准精神进 行评分. 2.评分标准中，如无特殊说明，均为累计给分. 3.评分过程中，只给整数分数. 一、选择题（每小题 3分，共 30 分） 题号 1 2 3 4 5 6 7 8 9 10 答案 B A A D D B D B C B 二、填空题（每小题 3分，功 15 分） 题号 11 12 13 14 15 答案 （3，﹣4） 8 15π 216° 60或 120 三、解答题（本大题共 8 小题，满分 75 分） 16.（1）方程整理得：x2﹣4x＝1， 配方得：x2﹣4x+4＝5，即（x﹣2）2＝5， 开方得：x﹣2＝± ， 解得：x1＝2+ ，x2＝2﹣ ；………………………………………………4分 （2）方程整理得：（x﹣1）2＝8， 开方得：x﹣1＝±2 ， 解得：x1＝1+2 ，x2＝1﹣2 ．……………………………………………4分 17. 设圆心为 O，过圆心 O作 MN⊥AD 于点 M，则 MN 平分 EF，连接 OF，设 OF=x， 则 OM=16-x，MF=8 ---2 分，在 Rt△OMF 中（16-x） 2 +8 2 =x 2 …………5 分 解得：x=10 答：球的半径为 10cm． …………………………………7 分 18．（1） ； ………………………………………………………………4分 （2）画树状图得： ∵共有 12 种等可能的结果，恰好是 2 名女生的有 6 种情况， ∴恰好是 2 名女生的概率为： ＝ ． -………………………………9 分 19.（1）连接 OD，∵AB=BC，∴∠A=∠C，∵AO=OD，∴∠A=∠ODA, ∴∠ODA=∠C ∴DO∥BC， ∵DE⊥BC，∴∠ODE=∠DEC=90°即 DE⊥OD，∵OD 为半径，∴DE 是⊙O切线；……5 分 （2）连接 OG，∵∠A=35°∴∠BOD=2∠A=70°∵DG⊥AB，OB 过圆心 O，∴弧 BG=弧 BD， ∴∠BOG=∠BOD=70°∴∠GOD=140°∴劣弧 DG 的长= 180 5140  = 9 35 ………10 分 20.（1）∵四边形 ABOC 为平行四边形， ∴AD∥OB，AD=OB=2，而 A 点坐标为（0，3）， ∴D 点坐标为（2，3），∴1﹣2m=2×3=6，m=﹣ ， ∴反比例函数解析式为 y= ．……………………………………………………4 分 （2）∵反比例函数 y= 的图象关于原点中心对称， ∴当点 P 与点 D 关于原点对称，则 OD=OP，此时 P 点坐标为（﹣2，﹣3）， ∵反比例函数 y= 的图象关于直线 y=x 对称， ∴点 P 与点 D（2，3）关于直线 y=x 对称时满足 OP=OD，此时 P 点坐标为（3，2）， 点（3，2）关于原点的对称点也满足 OP=OD，此时 P点坐标为（﹣3，﹣2）， 综上所述，P 点的坐标为（﹣2，﹣3），（3，2），（﹣3，﹣2）．…………10 分 21.（1）由题意：y＝x（4﹣x）＝﹣x2+4x．（两个结果都可以）………………2 分 （2）0＜x＜4． ……………………………………………………………………4 分 （3）1.75 ……………………………………………………………………………6 分 （4）函数图象如图所示： （第 22题图） 22.（1）当 1≤x≤20 时，令 30+ 2 1 x=35,解得 x=10， 当 21≤x≤40 时，令 20+ x 525 =35 ,解得 x=35，经检验得 x=35 是原方程的解且符合题意 即第 10 天 或者第 35 天该商品的销售单价为 35 元/件． ……………………………3分 （2）当 1≤x≤20 时，y=（30+ 2 1 x－20）（50－x）=- 2 1 x2+15x+500 当 21≤x≤40 时，y=(20+ x 525 －20）（50－x）= x 26250 －525 综上可知 y= - 2 1 x2+15x+500 ( 1≤x≤20 ) ……………………6 分 x 26250 －525 ( 21≤x≤40 ) （3）当 1≤x≤20 时，y=- 2 1 x2+15x+500=- 2 1 (x－15)2+612.5 ∵- 2 1 ＜0 ∴当 x=15 时，y有最大值 y1，且 y1=612.5， 当 21≤x≤40 时，∵26250＞0， ∴ x 26250 随 x 的减小而增大， ∴ 当 x=21 时， y有最大值 y2，且 y2=725 ∵y1＜y2，∴这 40 天中第 21 天时该网站获得利润最大，最大利润为 725 元．…10 分 23. （1）将 A（2，0）、B（8，6）代入 y＝ x2+bx+c， 得 ，解得： ， ∴二次函数的解析式为 y＝ x2﹣4x+6；…………………………………3 分 （2）∵二次函数解析式为 y＝ x2﹣4x+6， ∴二次函数图象的顶点坐标为（4，﹣2）． 当 y＝0 时，有 x2﹣4x+6＝0， 解得：x1＝2，x2＝6， ∴D 点的坐标为（6，0）； ………………………………………………7 分 （3）存在． 连接 CA，如图所示． ∵点 C 在二次函数的对称轴 x＝4 上， ∴点 C 的横坐标是 4，且 CA＝CD， ∴△CBD 的周长＝CD+CB+BD＝CA+CB+BD， 当点 A、C、B 三点共线时，CA+CB 最小． ……………………9 分 ∵BD 是定值， ∴当点 A、C、B 三点共线时，△CBD 的周长最小． 设直线 AB 的解析式为 y＝mx+n， 把 A（2，0）、B（8，6）代入 y＝mx+n， 得 ，解得： ， ∴直线 AB 的解析式为 y＝x﹣2． 当 x＝4 时，y＝x﹣2＝4﹣2＝2， ∴当点 C 的坐标为（4，2）时，△CBD 的周长最小．………………………11 分