北师大版七年级上册-第01讲- 丰富的图形世界 （提高）-学案 9页

1 学科教师辅导讲义 学员编号： 年 级：七年级 课 时 数：3 学员姓名： 辅导科目：数学 学科教师： 授课主题 第 01 讲—丰富的图形世界 授课类型 T 同步课堂 P 实战演练 S 归纳总结 教学目标 1 熟悉常见的立体图形，掌握特征与分类，特别是棱柱、圆柱；掌握点线面的关系 2 熟悉了解立体图形的展开折叠，尤其是正方体； 3 了解常见几何体截面的形状； 4 能够判断几何体的三视图形状，根据三视图推算几何体的形状。 授课日期及时段 T（Textbook-Based）——同步课堂 体系搭建 一、知识框架 常见的立体图形 展开与折叠 1、三视图的定义、判断 三视图 2、由三视图推算几何体的形状 截几何体： 常见几何体的截面 二、知识概念 （1）基本图形 1、棱柱（棱柱的定义、特点、分类） 圆柱（与棱柱的异同点） 椎体、球体 2、点线面的关系 1、正方形展开与折叠 2、常见几何体的展开与折叠 叠 2 几何图形：从实物中抽象出的各种图形叫几何图形．几何图形分为立体图形和平面图形。 立体图形：有些几何图形（如长方体、正方体、圆柱、圆锥、球等）的各部分不都在同一个平面内，这就 是立体图形。 （2）棱柱及其有关概念、点线面的关系 棱：在棱柱中，任何相邻两个面的交线，都叫做棱。 侧棱：相邻两个侧面的交线叫做侧棱。 n 棱柱有两个底面，n 个侧面，共（n+2）个面；3n 条棱，n 条侧棱；2n 个顶点。 点是所有图形的基础；线是点的移动轨迹，有长短、粗细之分；面就是由无数条线组成的。 （3）三视图 主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形。 （4）图形的展开和折叠 图形的展开：沿图形的表面的棱将图形展开。图形的折叠：将展开的平面图形折叠 正方体的展开图可以归为四大类：二二二型；三三型；二三一型（或一三二型）；一四一型。正方体的表 面展开图不能出现“田”字形与“凹”字形。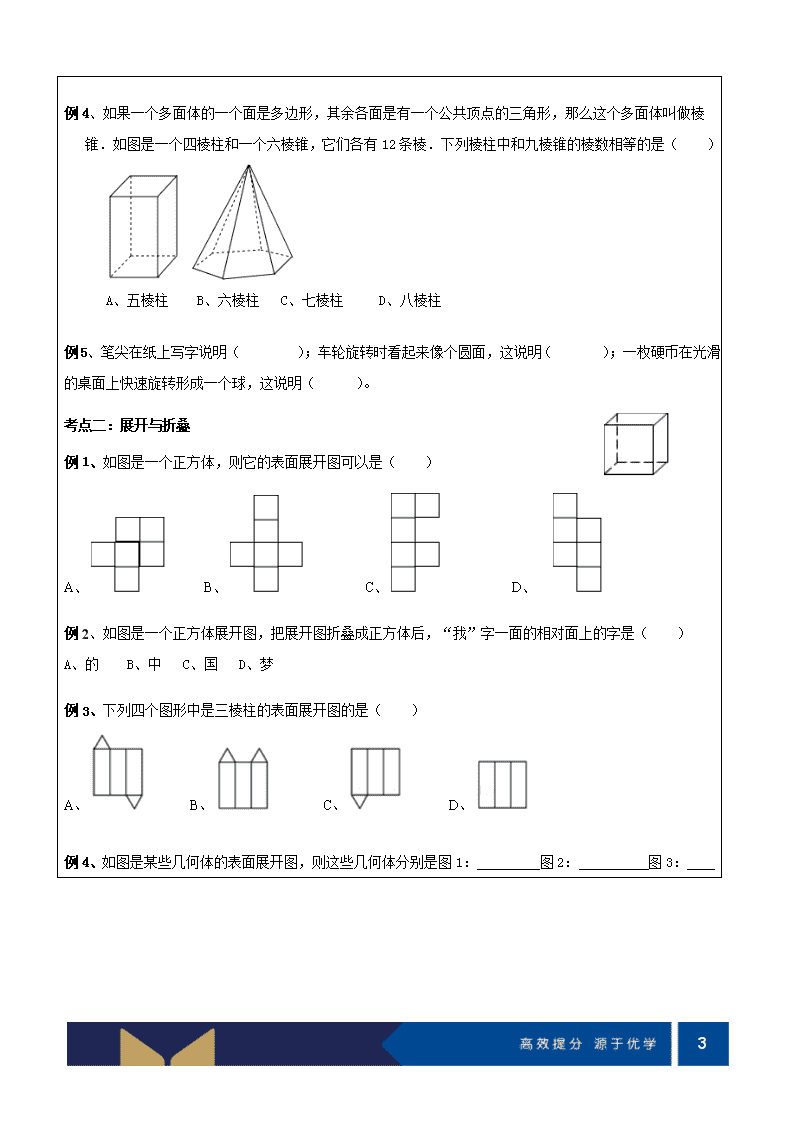 典例分析 考点一： 棱柱 例 1、下列图形属于棱柱的有（ ） A、2 个 B、3 个 C、4 个 D、5 个 例 2、对棱柱而言，下列说法错误的是（ ） A、所有侧面都是长方形 B、所有侧棱长都相等 C、上、下底面的形状相同 D、相邻两个侧面的交线叫做侧棱 例 3、下列说法中，正确的个数是（ ） ①柱体的两个底面一样大；②圆柱、圆锥的底面都是圆；③棱柱的底面是四边形；④长方体一定是柱体； ⑤棱柱的侧面一定是长方形 3 例 4、如果一个多面体的一个面是多边形，其余各面是有一个公共顶点的三角形，那么这个多面体叫做棱 锥．如图是一个四棱柱和一个六棱锥，它们各有 12 条棱．下列棱柱中和九棱锥的棱数相等的是（ ） A、五棱柱 B、六棱柱 C、七棱柱 D、八棱柱 例 5、笔尖在纸上写字说明（ ）；车轮旋转时看起来像个圆面，这说明（ ）；一枚硬币在光 滑的桌面上快速旋转形成一个球，这说明（ ）。 考点二：展开与折叠 例 1、如图是一个正方体，则它的表面展开图可以是（ ） A、 B、 C、 D、 例 2、如图是一个正方体展开图，把展开图折叠成正方体后，“我”字一面的 相对面上的字是（ ） A、的 B、中 C、国 D、梦 例 3、下列四个图形中是三棱柱的表面展开图的是（ ） A、 B、 C、 D、 例 4、如图是某些几何体的表面展开图，则这些几何体分别是 图 1： 图 2： 图 3： 4 例 5、如图的正方体盒子的外表面上画有 3 条粗黑线，将这个正方体盒子的表面展开（外 表面朝上），展开图可能是（ ） A、 B、 C、 D、 考点三： 三视图 例 1、下列四个立体图形中，主视图为圆的是（ ） A、 B、 C、 D、 菁优网 例 2、如图，在常见的几何体圆锥、圆柱、球、长方体中，主视图与它的左视图一 定完全相同的几何体有 （填编号） 权所 例 3、画出下图所示物体的三视图 例 4、一个物体由多个完全相同的小正方体组成，它的三视图如图所示，那么组 成这个物体的小正方体的个数为（ ） A、2 个 B、3 个 C、5 个 D、10 个 例 5、由一些大小相同的小正方体搭成的几何体的主视图和左视图如图，则搭成该几何体的小正方体的个数 5 最少是（ ） A、3 B、4 C、5 D、6 考点四：截几何体 例 1、一个几何体被一个平面所截后，得到一个圆形截面，则原几何体的形状是（ ） A、圆柱 B、圆锥 C、球 D、以上都可以 例 2、在下列几何体中，截面不是等腰梯形的是（ ） A、圆台 B、圆柱 C、正方体 D、三棱柱 例 3、用一平面去截如图 5 个几何体，能得到长方形截面的几何体的个数是（ ） A、4 B、3 C、2 D、1 P(Practice-Oriented)——实战演练 实战演练  课堂狙击 1、如下图，下列图形属于柱体的是（ ） A、 B、 C、 D、 2、请写出棱柱与圆柱的共同点_____、_____，以及不同点_____、_____（至 少二个） 6 3、如图绕虚线旋转得到的几何体是（ ） A、 B、 C、 D、 4、下面图形经过折叠不能围成棱柱的是（ ） A、 B、 C、 D、 5、下列图形中，不可以作为一个正方体的展开图的是（ ） A、 B、 C、 D、 6、如图是正方体的平面展开图，每个面上都标有一个汉字，与“自”字相对的面上的字是 7、将如图所示表面带有图案的正方体沿某些棱展开后，得到的图形是（ ） A、 B、 C、 D、 8、如图是由一些大小相同的小立方体组成的几何体的主视图和左视图，则组成这 个几何体的 小立方体的个数不可能是（ ） A、3 B、4 C、5 D、6 9、超市货架上摆放着某品牌方便面，如图是它们的三视图，则货架上的方便 面至少有（ ） 7 A、8 B、9 C、10 D、11 10、一个正方体物体，被切一刀后，它的切面不可能是 （写出所有的答案）  课后反击 1、下列说法中，正确的有（ ） ①圆锥和圆柱的底面都是圆 ②棱锥底面边数与侧棱数相等 ③棱柱的上下底面是形状、大小相同的多边形 ④正方体是四棱柱，四棱柱是正方体 A、1 个 B、2 个 C、3 个 D、4 个 2、下面的几何体中，属于棱柱的有（ ） A、1 个 B、2 个 C、3 个 D、4 个 3、下列第二行的哪种几何体 的表面能展开成第一行的平面图形？请对应连线 有 4、小军将 一个直角三角板（如下左图）绕它的 一条直角边所在的直线旋转一周形成一个几何，将这个几何 8 体的侧面展开得到的大致图形是（ ） A、 B、 C、 D、 5、下列各图不是正方体表面展开图的是（ ） A． B． C． D． 6、 如图，为一正方体的侧面展开图，那么“于”字所在的面与“ ”字所在的面是对面。 7、如图所示，这个几何体的展开图形是（ ） A、 B、 C、 D、 8、一个由小立方块搭成的几何体，从正面、左面、上面看到的形状图如图所示，这 个几何体 是由（ ）个小立方块搭成的。 A、4 B、5 C、6 D、7 9、用一个平面去截一个几何体，若截面是长方形， 则该几何体可能是_____、_____、 _____、（写三个） 直击中考 1、【2016 深圳】把下列图形折成一个正方体的盒子，折好后与“中”相对的字是（ ） A、祝 B、你 C、顺 D、利 2、【2015 深圳】下列主视图正确的是（ ） 9 3、由几个大小不同的正方形组成的几何 图形如图，则它的俯视图是（ ） A、 B、 C、 D、 S(Summary-Embedded)——归纳总结 重点回顾 1、棱柱（棱柱的定义、特点、分类） 2、正方形展开与折叠 3、三视图 名师点拨 1、正方体的展开图可以归为四大类：二二二型；三三型；二三一型（或一三二型）；一四一型。正方体的 表面展开图不能出现“田”字形与“凹”字形 2、通过三视图判断几何体形状：俯视图打地基，正视图疯狂盖，左视图拆违章 学霸经验  本节课我学到  我需要努力的地方