- 443.50 KB
- 2021-10-21 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2019-2020学年北京市101中学石油分校七年级(下)期末数学试卷
一.选择题(共10小题)
1.下列计算正确的是( )
A.=±5 B.=﹣3 C. D.
2.下列语句正确的是( )
A.平行于x轴的直线上所有点的横坐标都相同
B.(﹣3,5)与(5,﹣3)表示两个不同的点
C.若点P(a,b)在y轴上,则b=0
D.若点P(﹣3,4),则P到x轴的距离为3
3.如图所示的车标,可以看作由“基本图案”经过平移得到的是( )
A. B.
C. D.
4.如图,有以下四个条件:①∠B+∠BCD=180°,②∠1=∠2,③∠3=∠4,④∠B=∠5,其中能判定AB∥CD的条件的个数有( )
A.1 B.2 C.3 D.4
5.已知a<b,下列不等式中,正确的是( )
A.a+4>b+4 B.a﹣3>b﹣3 C.a<b D.﹣2a<﹣2 b
6.红领巾公园健走步道环湖而建,以红军长征路为主题,如图是利用平面直角坐标系画出的健走步道路线上主要地点的大致分布图,这个坐标系分别以正东、正北方向为x轴、y轴的正方向,如果表示遵义的点的坐标为(﹣5,7),表示腊子口的点的坐标为(4,﹣1),那么这个平面直角坐标系原点所在位置是( )
A.泸定桥 B.瑞金 C.包座 D.湘江
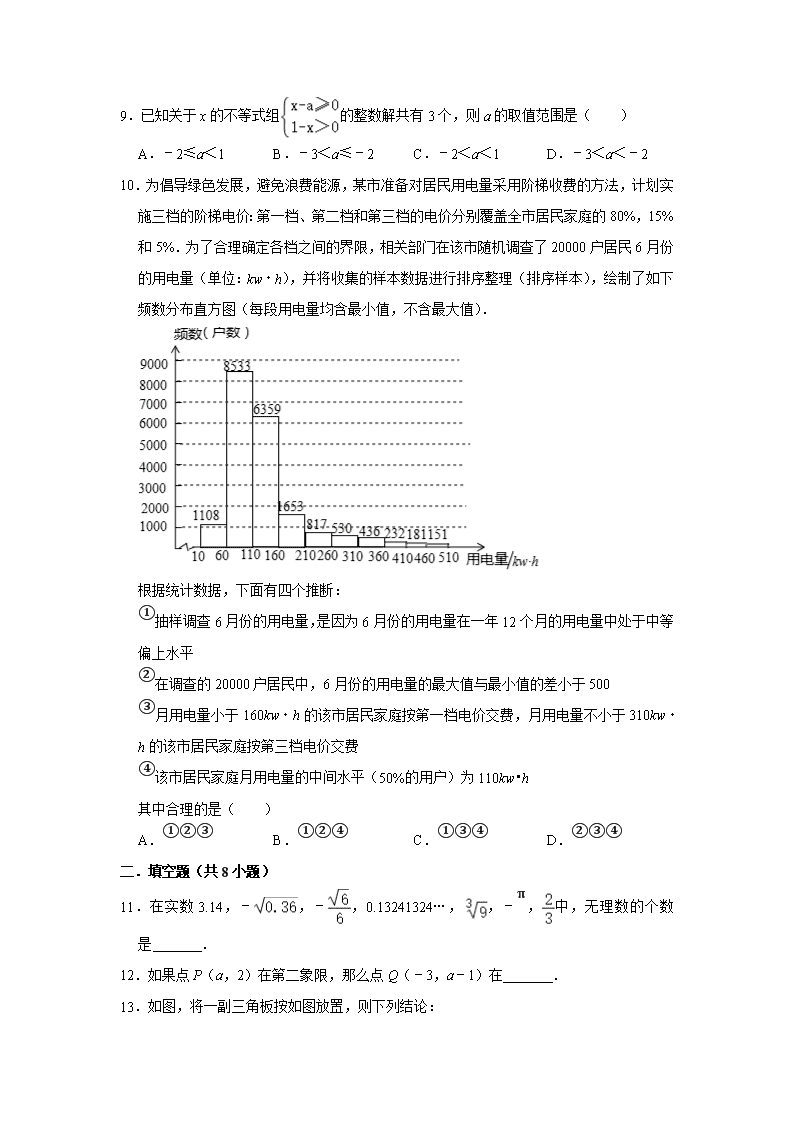
7.荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,下列结论错误的是( )
A.本次抽样调查的样本容量是5000
B.扇形图中的m为10%
C.样本中选择公共交通出行的有2500人
D.若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有25万人
8.我国古代数学著作《增删算法统宗》记载”绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.“其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,则符合题意的方程组是( )
A. B.
C. D.
9.已知关于x的不等式组的整数解共有3个,则a的取值范围是( )
A.﹣2≤a<1 B.﹣3<a≤﹣2 C.﹣2<a<1 D.﹣3<a<﹣2
10.为倡导绿色发展,避免浪费能源,某市准备对居民用电量采用阶梯收费的方法,计划实施三档的阶梯电价:第一档、第二档和第三档的电价分别覆盖全市居民家庭的80%,15%和5%.为了合理确定各档之间的界限,相关部门在该市随机调查了20000户居民6月份的用电量(单位:kw・h),并将收集的样本数据进行排序整理(排序样本),绘制了如下频数分布直方图(每段用电量均含最小值,不含最大值).
根据统计数据,下面有四个推断:
①抽样调查6月份的用电量,是因为6月份的用电量在一年12个月的用电量中处于中等偏上水平
②在调查的20000户居民中,6月份的用电量的最大值与最小值的差小于500
③月用电量小于160kw・h的该市居民家庭按第一档电价交费,月用电量不小于310kw・h的该市居民家庭按第三档电价交费
④该市居民家庭月用电量的中间水平(50%的用户)为110kw•h
其中合理的是( )
A.①②③ B.①②④ C.①③④ D.②③④
二.填空题(共8小题)
11.在实数3.14,﹣,﹣,0.13241324…,,﹣π,中,无理数的个数是 .
12.如果点P(a,2)在第二象限,那么点Q(﹣3,a﹣1)在 .
13.如图,将一副三角板按如图放置,则下列结论:
①∠1=∠3;
②如果∠2=30°,则有BC∥AE;
③如果∠1=∠2=∠3,则有BC∥AE;
④如果∠2=45°,必有∠4=∠E.其中正确的有 (填序号).
14.若关于x,y的二元一次方程组的解也是二元一次方程x﹣3y=6的解,则k= .
15.如图,在实数范围内规定新运算“△”,其规则是:a△b=2a﹣b.已知不等式x△k≥1的解集在数轴上,则k的值是 .
16.如图,AB∥ED,∠CAB=135°,∠ACD=75°,则∠CDE= 度.
17.如表所示,被开方数a的小数点位置移动和它的算术平方根的小数点位置移动规律符合一定的规律,若=180,且=﹣1.8,则被开方数a的值为 .
a
…
0.000001
0.01
1
100
10000
1000000
…
…
0.001
0.1
1
10
100
1000
…
18.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为 (用n表示).
三.解答题
19.计算
(1);
(2).
20.解下列方程组:
(1)
(2).
21.解不等式
(1)解不等式组
(2)解不等式组,并写出它的所有非负整数解.
.
22.完成下面推理过程:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2 ( )
且∠1=∠CGD( ),
∴∠2=∠CGD ( )
∴CE∥BF( ).
∴∠ BFD =∠C( ).
又∵∠B=∠C ( )
∴∠ BFD =∠B ( )
∴AB∥CD( ).
23.如图,计划围一个面积为50m2的长方形场地,一边靠旧墙(墙长为10m),另外三边用篱笆围成,并且它的长与宽之比为5:2.讨论方案时,小英说:“我们不可能围成满足要求的长方形场地.”小军说:“面积和长宽比例是确定的,肯定可以围得出来.”请你判断谁的说法正确,为什么?
24.△ABC在平面直角坐标系中,且A(﹣2,1)、B(﹣3,﹣2)、C(1,﹣4).将其平移后得到△A1B1C1,若A,B的对应点是A1,B1,C的对应点C1的坐标是(3,﹣1)
(1)在平面直角坐标系中画出△ABC;
(2)写出点A1的坐标是 ,B1坐标是 ;
(3)此次平移也可看作△A1B1C1向 平移了 个单位长度,再向 平移了 个单位长度得到△ABC.
25.已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,求证:AB∥CD.
26.国家发改委、工业和信息化部、财政部公布了“节能产品惠民工程”,公交公司积极响应将旧车换成节能环保公交车,计划购买A型和B型两种环保型公交车10辆,其中每台的价格、年载客量如表:
A型
B型
价格(万元/台)
x
y
年载客量/万人次
60
100
若购买A型环保公交车1辆,B型环保公交车2辆,共需400万元;若购买A型环保公交车2辆,B型环保公交车1辆,共需350万元.
(1)求x、y的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保10辆公交车在该线路的年载客量总和不少于680万人次,问有哪几种购买方案?
(3)在(2)的条件下,哪种方案使得购车总费用最少?最少费用是多少万元?
27.为了解2020年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作了不完整的频数分布表.
分数x(分)
频数
百分比
60≤x<70
30
10%
70≤x<80
90
n
80≤x<90
m
40%
90≤x≤100
60
20%
请根据图表提供的信息,解答下列问题:
(1)本次调查的样本容量为 ;
(2)在表中:m= ;n= ;
(3)根据频数分布表画频数分布直方图;
(4)如果比赛成绩在80分以上(含80分)为优秀,那么你估计参加该竞赛项目的的30000人中,优秀人数大约是 .
28.对于平面直角坐标系xOy中的点P(a,b),若P'(a+kb,ka+b)(其中k为常数,且k≠0),则称点P″为点P的“k属派生点”.例如:P (1,4)的“2属派生点”为P'(1+2×4,2×1+4),即P (9,6).
(1)点P(﹣2,3)的“3属派生点”P''的坐标为 .
(2)若点P的“5属派生点”P'的坐标为(3,﹣9),求点P的坐标.
(3)若点P在x轴的正半轴上,点P的“k属派生点”为P''点,且线段PP'的长度为线段OP长度的2倍,求k的值.
2019-2020学年北京市101中学石油分校七年级(下)期末数学试卷
参考答案与试题解析
一.选择题(共10小题)
1.下列计算正确的是( )
A.=±5 B.=﹣3 C. D.
【分析】分别利用平方根、立方根、算术平方根的性质计算即可得出答案.
【解答】解:A.=5,故此选项错误;
B.=3,故此选项错误;
C.=5,故此选项错误;
D.=﹣3,故此选项正确.
故选:D.
2.下列语句正确的是( )
A.平行于x轴的直线上所有点的横坐标都相同
B.(﹣3,5)与(5,﹣3)表示两个不同的点
C.若点P(a,b)在y轴上,则b=0
D.若点P(﹣3,4),则P到x轴的距离为3
【分析】根据平行与坐标轴的直线上点的坐标特点、坐标的概念、坐标轴上点的坐标特点及点到坐标轴的距离等知识点逐一判断即可得.
【解答】解:A.平行于x轴的直线上所有点的纵坐标都相同,此选项错误;
B.(﹣3,5)与(5,﹣3)表示两个不同的点,此选项正确;
C.若点P(a,b)在y轴上,则a=0,此选项错误;
D.若点P(﹣3,4),则P到x轴的距离为4,此选项错误;
故选:B.
3.如图所示的车标,可以看作由“基本图案”经过平移得到的是( )
A. B.
C. D.
【分析】根据平移的概念:在平面内,把一个图形整体沿某一的方向移动,这种图形的平行移动,叫做平移变换,简称平移,即可选出答案.
【解答】解:根据平移的概念,观察图形可知图案B通过平移后可以得到.
故选:B.
4.如图,有以下四个条件:①∠B+∠BCD=180°,②∠1=∠2,③∠3=∠4,④∠B=∠5,其中能判定AB∥CD的条件的个数有( )
A.1 B.2 C.3 D.4
【分析】根据平行线的判定定理求解,即可求得答案.
【解答】解:①∵∠B+∠BDC=180°,
∴AB∥CD;
②∵∠1=∠2,
∴AD∥BC;
③∵∠3=∠4,
∴AB∥CD;
④∵∠B=∠5,
∴AB∥CD;
∴能得到AB∥CD的条件是①③④.
故选:C.
5.已知a<b,下列不等式中,正确的是( )
A.a+4>b+4 B.a﹣3>b﹣3 C.a<b D.﹣2a<﹣2 b
【分析】根据不等式的性质,可得答案.
【解答】解:A、两边都加4,不等号的方向不变,故A错误;
B、两边都减3,不等号的方向不变,故B错误;
C、两边都乘,不等号的方向不变,故C正确;
D、两边都乘﹣2,不等号的方向改变,故D错误;
故选:C.
6.红领巾公园健走步道环湖而建,以红军长征路为主题,如图是利用平面直角坐标系画出的健走步道路线上主要地点的大致分布图,这个坐标系分别以正东、正北方向为x轴、y轴的正方向,如果表示遵义的点的坐标为(﹣5,7),表示腊子口的点的坐标为(4,﹣1),那么这个平面直角坐标系原点所在位置是( )
A.泸定桥 B.瑞金 C.包座 D.湘江
【分析】直接利用遵义和腊子口的位置进而确定原点的位置.
【解答】解:如图所示:平面直角坐标系原点所在位置是瑞金.
故选:B.
7.荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,下列结论错误的是( )
A.本次抽样调查的样本容量是5000
B.扇形图中的m为10%
C.样本中选择公共交通出行的有2500人
D.若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有25万人
【分析】结合条形图和扇形图,求出样本人数,进而进行解答.
【解答】解:A、本次抽样调查的样本容量是=5000,正确;
B、扇形图中的m为10%,正确;
C、样本中选择公共交通出行的有5000×50%=2500人,正确;
D、若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有50×40%=20万人,错误;
故选:D.
8.我国古代数学著作《增删算法统宗》记载”绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.“其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,则符合题意的方程组是( )
A. B.
C. D.
【分析】设索长为x尺,竿子长为y尺,根据“索比竿子长一托,折回索子却量竿,却比竿子短一托”,即可得出关于x、y的二元一次方程组.
【解答】解:设索长为x尺,竿子长为y尺,
根据题意得:.
故选:A.
9.已知关于x的不等式组的整数解共有3个,则a的取值范围是( )
A.﹣2≤a<1 B.﹣3<a≤﹣2 C.﹣2<a<1 D.﹣3<a<﹣2
【分析】表示出不等式组的解集,由不等式组的整数解共有3个,确定出a的范围即可.
【解答】解:不等式组整理得:,
解得:a≤x<1,
由不等式组的整数解有3个,得到整数解为﹣2,﹣1,0,
则a的范围为﹣3<a≤﹣2.
故选:B.
10.为倡导绿色发展,避免浪费能源,某市准备对居民用电量采用阶梯收费的方法,计划实施三档的阶梯电价:第一档、第二档和第三档的电价分别覆盖全市居民家庭的80%,15%和5%.为了合理确定各档之间的界限,相关部门在该市随机调查了20000户居民6月份的用电量(单位:kw・h),并将收集的样本数据进行排序整理(排序样本),绘制了如下频数分布直方图(每段用电量均含最小值,不含最大值).
根据统计数据,下面有四个推断:
①抽样调查6月份的用电量,是因为6月份的用电量在一年12个月的用电量中处于中等偏上水平
②在调查的20000户居民中,6月份的用电量的最大值与最小值的差小于500
③月用电量小于160kw・h的该市居民家庭按第一档电价交费,月用电量不小于310kw・h的该市居民家庭按第三档电价交费
④该市居民家庭月用电量的中间水平(50%的用户)为110kw•h
其中合理的是( )
A.①②③ B.①②④ C.①③④ D.②③④
【分析】根据统计图中的数据可以判断各个小题是否成立,从而可以解答本题.
【解答】解:由题意可得,
抽样调查6月份的用电量,是因为6月份的用电量在一年12个月的用电量中处于中等偏上水平,故①合理,
在调查的20000户居民中,6月份的用电量的最大值与最小值的差小于510﹣10=500,故②合理,
第一档用户数量为:20000×80%=16000户,由1108+8533+6359=16000,故月用电量小于160kw・h的该市居民家庭按第一档电价交费,
第三档用户数量为:20000×5%=1000户,由151+181+232+436=1000,故月用电量不小于310kw・h的该市居民家庭按第三档电价交费,故③合理,
该市居民家庭月用电量的中间水平(50%的用户)为大于等于110kw•h,小于160kw•h,故④不合理,
故选:A.
二.填空题(共8小题)
11.在实数3.14,﹣,﹣,0.13241324…,,﹣π,中,无理数的个数是 3 .
【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【解答】解:3.14、﹣=﹣0.6、0.13241324…、这四个数是有理数,
﹣、和﹣π这三个数是无理数,
故答案为:3.
12.如果点P(a,2)在第二象限,那么点Q(﹣3,a﹣1)在 第三象限 .
【分析】根据各象限内点的坐标特征解答即可.
【解答】解:由题意,得
a<0,
a﹣1<﹣1,
点Q(﹣3,a﹣1)在第三象限,
故答案为:第三象限.
13.如图,将一副三角板按如图放置,则下列结论:
①∠1=∠3;
②如果∠2=30°,则有BC∥AE;
③如果∠1=∠2=∠3,则有BC∥AE;
④如果∠2=45°,必有∠4=∠E.其中正确的有 ①③ (填序号).
【分析】根据平行线的判定和性质解答即可.
【解答】解:∵∠EAD=∠CAB=90°,
∴∠1=∠3,故①正确,
当∠2=30°时,∠3=60°,∠4=45°,
∴∠3≠∠4,
故AE与BC不平行,故②错误,
当∠1=∠2=∠3时,可得∠3=∠4=45°,
∴BC∥AE,故③正确,
∵∠E=60°,∠4=45°,
∴∠E≠∠4,故④错误,
故答案为:①③.
14.若关于x,y的二元一次方程组的解也是二元一次方程x﹣3y=6的解,则k= 1 .
【分析】把k看做已知数表示出方程组的解,代入已知方程求出k的值即可.
【解答】解:,
①+②得:2x=6k,即x=3k,
②﹣①得:2y=﹣2k,即y=﹣k,
把x=3k,y=﹣k代入x﹣3y=6中得:3k+3k=6,
解得:k=1,
故答案为:1
15.如图,在实数范围内规定新运算“△”,其规则是:a△b=2a﹣b.已知不等式x△k≥1的解集在数轴上,则k的值是 k=﹣3 .
【分析】根据新运算法则得到不等式2x﹣k≥1,通过解不等式即可求k的取值范围,结合图象可以求得k的值.
【解答】解:根据图示知,已知不等式的解集是x≥﹣1.
则2x﹣1≥﹣3
∵x△k=2x﹣k≥1,
∴2x﹣1≥k且2x﹣1≥﹣3,
∴k=﹣3.
故答案是:k=﹣3.
16.如图,AB∥ED,∠CAB=135°,∠ACD=75°,则∠CDE= 30 度.
【分析】过C作CF∥AB,根据平行线性质得出∠ACF+∠CAB=180°,∠CDE=∠FCD,求出∠ACF,求出∠DCF即可.
【解答】解:
过C作CF∥AB,
∵DE∥AB,
∴AB∥CF∥DE,
∴∠ACF+∠CAB=180°,∠CDE=∠FCD,
∵∠CAB=135°,
∴∠ACF=45°,
∵∠ACD=75°,
∴∠FCD=30°,
∴∠EDC=30°,
故答案为:30.
17.如表所示,被开方数a的小数点位置移动和它的算术平方根的小数点位置移动规律符合一定的规律,若=180,且=﹣1.8,则被开方数a的值为 32400 .
a
…
0.000001
0.01
1
100
10000
1000000
…
…
0.001
0.1
1
10
100
1000
…
【分析】根据题意和表格中数据的变化规律,可以求得a的值.
【解答】解:∵=180,且﹣=﹣1.8,
∴=1.8,
∴=180,
∴a=32400,
故答案为:32400.
18.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为 (2n,1) (用n表示).
【分析】根据图形分别求出n=1、2、3时对应的点A4n+1的坐标,然后根据变化规律写出即可.
【解答】解:由图可知,n=1时,4×1+1=5,点A5(2,1),
n=2时,4×2+1=9,点A9(4,1),
n=3时,4×3+1=13,点A13(6,1),
所以,点A4n+1(2n,1).
故答案为:(2n,1).
三.解答题
19.计算
(1);
(2).
【分析】(1)利用开立方的运算法则和实数的分配律运算即可;
(2)首先进行平方运算,绝对值得化简,开方运算,再进行加减运算即可.
【解答】解(1)原式=﹣3+
=;
(2)原式=﹣9﹣2
=﹣8.
20.解下列方程组:
(1)
(2).
【考点】98:解二元一次方程组.
【专题】11:计算题.
【分析】(1)利用①×3﹣②可解出y,再把y的值代入①可求出x,从而得到方程组的解;
(2)利用①×3+②×2得9x+10x=48+66,可求出x,再把x的值代入①可求出y,从而得到方程组的解.
【解答】解:(1),
①×3﹣②得5y=﹣5,
解得y=﹣1,
把y=﹣1代入①得x+1=3,
解得x=2,
所以方程组的解为;
(2),
①×3+②×2得9x+10x=48+66,
解得x=6,
把x=6代入①得18+4y=16,
解得y=﹣,
所以方程组的解为.
21.解不等式
(1)解不等式组
(2)解不等式组,并写出它的所有非负整数解.
【考点】CB:解一元一次不等式组;CC:一元一次不等式组的整数解.
【专题】524:一元一次不等式(组)及应用;66:运算能力.
【分析】(1)分别求出不等式组中两不等式的解集,找出两解集的公共部分即可;
(2)分别求出不等式组中两不等式的解集,找出两解集的公共部分确定出不等式组的解集,进而求出所有非负整数解即可.
【解答】解:(1),
由①得:x≥﹣1,
由②得:x<3,
则不等式组的解集为﹣1≤x<3;
(2),
由①得:x>﹣2,
由②得:x≤,
∴不等式组的解集为﹣2<x≤,
则不等式组的所有非负整数解为0,1.
22.完成下面推理过程:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2 ( 已知 )
且∠1=∠CGD( 对顶角相等 ),
∴∠2=∠CGD ( 等量代换 )
∴CE∥BF( 同位角相等,两直线平行 ).
∴∠ BFD =∠C( 两直线平行,同位角相等 ).
又∵∠B=∠C ( 已知 )
∴∠ BFD =∠B ( 等量代换 )
∴AB∥CD( 内错角相等,两直线平行 ).
【考点】JB:平行线的判定与性质.
【专题】551:线段、角、相交线与平行线.
【分析】先确定∠1=∠CGD是对顶角,利用等量代换,求得∠2=∠CGD,则可根据:同位角相等,两直线平行,证得:CE∥BF,又由两直线平行,同位角相等,证得角相等,易得:∠BFD=∠B,则利用内错角相等,两直线平行,即可证得:AB∥CD.
【解答】解:∵∠1=∠2 (已知),且∠1=∠CGD(对顶角相等),
∴∠2=∠CGD (等量代换),
∴CE∥BF(同位角相等,两直线平行).
∴∠BFD=∠C(两直线平行,同位角相等).
又∵∠B=∠C (已知),
∴∠BFD=∠B (等量代换),
∴AB∥CD(内错角相等,两直线平行).
故答案为:已知,对顶角相等,等量代换,同位角相等,两直线平行,BFD
,两直线平行,同位角相等,已知,BFD,等量代换,内错角相等,两直线平行.
23.如图,计划围一个面积为50m2的长方形场地,一边靠旧墙(墙长为10m),另外三边用篱笆围成,并且它的长与宽之比为5:2.讨论方案时,小英说:“我们不可能围成满足要求的长方形场地.”小军说:“面积和长宽比例是确定的,肯定可以围得出来.”请你判断谁的说法正确,为什么?
【考点】22:算术平方根;AD:一元二次方程的应用.
【分析】根据矩形的面积公式求出矩形的长和宽,最后进行判断即可得出结论.
【解答】解:设长方形场地的长为5xm,宽为2xm,依题意,得,
5x•2x=50,
∴x=,
长为5,宽为2.
∵4<5<9,
∴2<<3.
由上可知2<6,且5>10
若长与墙平行,墙长只有10 m,故不能围成满足条件的长方形场地;
若宽与墙平行,则能围成满足条件的长方形场地.
∴他们的说法都不正确.
24.△ABC在平面直角坐标系中,且A(﹣2,1)、B(﹣3,﹣2)、C(1,﹣4).将其平移后得到△A1B1C1,若A,B的对应点是A1,B1,C的对应点C1的坐标是(3,﹣1)
(1)在平面直角坐标系中画出△ABC;
(2)写出点A1的坐标是 (0,4) ,B1坐标是 (﹣1,1) ;
(3)此次平移也可看作△A1B1C1向 下 平移了 3 个单位长度,再向 左 平移了 2 个单位长度得到△ABC.
【考点】Q4:作图﹣平移变换.
【专题】13:作图题;558:平移、旋转与对称.
【分析】(1)根据A,B,C三点坐标画出图形,再作出A,B的对应点A1,B1即可;
(2)根据A1,B1的位置写出坐标即可.
(3)观察图象利用平移性质解决问题即可.
【解答】解:(1)△ABC,△A1B1C1如图所示.
(2)点A1的坐标是(0,4),B1坐标是(﹣1,1).
故答案为(0,4),(﹣1,1).
(3)此次平移也可看作△A1B1C1向下平移了3个单位长度,再向左平移了2个单位长度得到△ABC.
故答案为下,3;左,2;
25.已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,求证:AB∥CD.
【考点】JB:平行线的判定与性质.
【专题】14:证明题.
【分析】首先由AE⊥BC,FG⊥BC可得AE∥FG,根据两直线平行,同位角相等及等量代换可推出∠A=∠2,利用内错角相等,两直线平行可得AB∥CD.
【解答】证明:∵AE⊥BC,FG⊥BC,
∴∠AMB=∠GNM=90°,
∴AE∥FG,
∴∠A=∠1;
又∵∠2=∠1,
∴∠A=∠2,
∴AB∥CD.
26.国家发改委、工业和信息化部、财政部公布了“节能产品惠民工程”,公交公司积极响应将旧车换成节能环保公交车,计划购买A型和B型两种环保型公交车10辆,其中每台的价格、年载客量如表:
A型
B型
价格(万元/台)
x
y
年载客量/万人次
60
100
若购买A型环保公交车1辆,B型环保公交车2辆,共需400万元;若购买A型环保公交车2辆,B型环保公交车1辆,共需350万元.
(1)求x、y的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保10辆公交车在该线路的年载客量总和不少于680万人次,问有哪几种购买方案?
(3)在(2)的条件下,哪种方案使得购车总费用最少?最少费用是多少万元?
【考点】9A:二元一次方程组的应用;CE:一元一次不等式组的应用.
【专题】521:一次方程(组)及应用;524:一元一次不等式(组)及应用;69:应用意识.
【分析】(1)根据“购买A型环保公交车1辆,B型环保公交车2辆,共需400万元;若购买A型环保公交车2辆,B型环保公交车1辆,共需350万元”列出二元一次方程组求解可得;
(2)购买A型环保公交车m辆,则购买B型环保公交车(10﹣m)辆,根据“总费用不超过1200万元、年载客量总和不少于680万人次”列一元一次不等式组求解可得;
(3)设购车总费用为w万元,根据总费用的数量关系得出w=100m+150(10﹣m)=﹣50m+1500,再进一步利用一次函数的性质求解可得.
【解答】解:(1)由题意,得,
解得;
(2)设购买A型环保公交车m辆,则购买B型环保公交车(10﹣m)辆,
由题意,得,
解得6≤m≤8,
∵m为整数,
∴有三种购车方案
方案一:购买A型公交车6辆,购买B型公交车4辆;
方案二:购买A型公交车7辆,购买B型公交车3辆;
方案三:购买A型公交车8辆,购买B型公交车2辆.
(3)设购车总费用为w万元
则w=100m+150(10﹣m)=﹣50m+1500,
∵﹣50<0,6≤m≤8且m为整数,
∴m=8时,w最小=1100,
∴购车总费用最少的方案是购买A型公交车8辆,购买B型公交车2辆,购车总费用为1100万元.
27.为了解2020年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作了不完整的频数分布表.
分数x(分)
频数
百分比
60≤x<70
30
10%
70≤x<80
90
n
80≤x<90
m
40%
90≤x≤100
60
20%
请根据图表提供的信息,解答下列问题:
(1)本次调查的样本容量为 300 ;
(2)在表中:m= 120 ;n= 30% ;
(3)根据频数分布表画频数分布直方图;
(4)如果比赛成绩在80分以上(含80分)为优秀,那么你估计参加该竞赛项目的的30000人中,优秀人数大约是 18000 .
【考点】V3:总体、个体、样本、样本容量;V5:用样本估计总体;V7:频数(率)分布表;V8:频数(率)分布直方图.
【专题】541:数据的收集与整理;542:统计的应用;66:运算能力;69:应用意识.
【分析】(1)分数在60≤x<70的频数是30,占调查总数的10%,可求出调查总数,即样本容量;
(2)根据频数所占总数的百分比即可求m、n的值;
(3)根据频数补全频数分布直方图;
(4)样本估计总体,样本中“优秀”的占40%+20%=60%,因此估计总体30000人的60%是“优秀”人数.
【解答】解:(1)30÷10%=300(人),
故答案为300;
(2)m=300×40%=120(人),n=90÷300=30%,
故答案为:120,30%;
(3)根据频数,画出频数分布直方图;
(4)30000×(40%+20%)=18000(人),
故答案为:18000.
28.对于平面直角坐标系xOy中的点P(a,b),若P'(a+kb,ka+b)(其中k为常数,且k≠0),则称点P″为点P的“k属派生点”.例如:P (1,4)的“2属派生点”为P'(1+2×4,2×1+4),即P (9,6).
(1)点P(﹣2,3)的“3属派生点”P''的坐标为 (7,﹣3) .
(2)若点P的“5属派生点”P'的坐标为(3,﹣9),求点P的坐标.
(3)若点P在x轴的正半轴上,点P的“k属派生点”为P''点,且线段PP'的长度为线段OP长度的2倍,求k的值.
【考点】D5:坐标与图形性质.
【专题】532:函数及其图像.
【分析】(1)根据“k属派生点”计算可得;
(2)设点P的坐标为(x、y),根据“k属派生点”定义及P′的坐标列出关于x、y的方程组,解之可得;
(3)先得出点P′的坐标为(a,ka),由线段PP′的长度为线段OP长度的2倍列出方程,解之可得.
【解答】解:(1)点P(﹣2,3)的“3属派生点”P′的坐标为(﹣2+3×3,﹣2×3+3),即(7,﹣3),
故答案为:(7,﹣3);
(2)设P点的坐标是(a,b),
依题意得;,
解得:,
∴点P的坐标是(﹣2,1);
(2)∵点P在x轴的正半轴上,
∴设P点的坐标为(a,0)(a>0)
又∵点P的“k属派生点”为P''点,
∴设P''的坐标为(a,ka),
又∵线段PP''的长度是OP长度的2倍
∴PP''=2OP,
即:|ka|=|2a|,
又∵a>0,
∴k=±2.