探索平行线的性质教案(1) 4页

‎ ‎ ‎7.2探索平行线的性质 学习目标：‎ ‎1.掌握平行线的性质.‎ ‎2.运用平行线的性质及判定方法解决问题.‎ 学习重点：三条性质的推导；运用平行线的性质及判定方法解决问题.‎ 学习难点：运用平行线的性质及判定方法解决问题时的过程.‎ ‎1‎ A D E F ‎ ‎ ‎ B C ‎2‎ 导学过程：‎ ‎【预习交流】‎ ‎1.预习课本P11到P13，有哪些疑惑？‎ ‎2.若∠1与∠2是同旁内角，∠1=50º，则（ ）‎ ‎ A.∠2=50º B.∠2=130º C.∠2=50º或∠2=130º D.∠2的大小不定 ‎3.如图，∠A与哪个角相等时，AB∥EF （ ）‎ ‎ A.∠A =∠2 B.∠1=∠2 C.∠A=∠CEF D、∠A+∠AEF=180º ‎ ‎【点评释疑】‎ ‎1.课本P11数学实验室.‎ 两直线平行，同位角相等. 两直线平行，内错角相等. 两直线平行，同旁内角互补.‎ ‎2.课本P12议一议.‎ 根据“两直线平行，内错角相等”， 根据“两直线平行，同位角相等”，‎ 说明“两直线平行，内错角相等”. 说明“两直线平行，同旁内角互补” ‎ 如图∵a∥b（ ） 如图∵a∥b（ ）‎ ‎∴∠1=∠2（ ） ∴∠1=∠2（ ）‎ ‎∵∠1=∠3（ ） ∵∠1+∠3=180（ ）‎ ‎∴∠ =∠ （ ） ∴∠ +∠ =180（ ）‎ ‎3.如图，AD∥BC，∠A＝∠C．AB与DC平行吗？为什么？‎ 解：AB∥DC ‎∵AD∥BC（ ）‎ ‎∴∠A＝∠ABF（ ）‎ ‎∵∠A＝∠C( )‎ ‎∴∠ ＝∠ ( )‎ ‎∴ ∥ ( )‎ 4‎ ‎ ‎ 你还有其他的证明方法吗？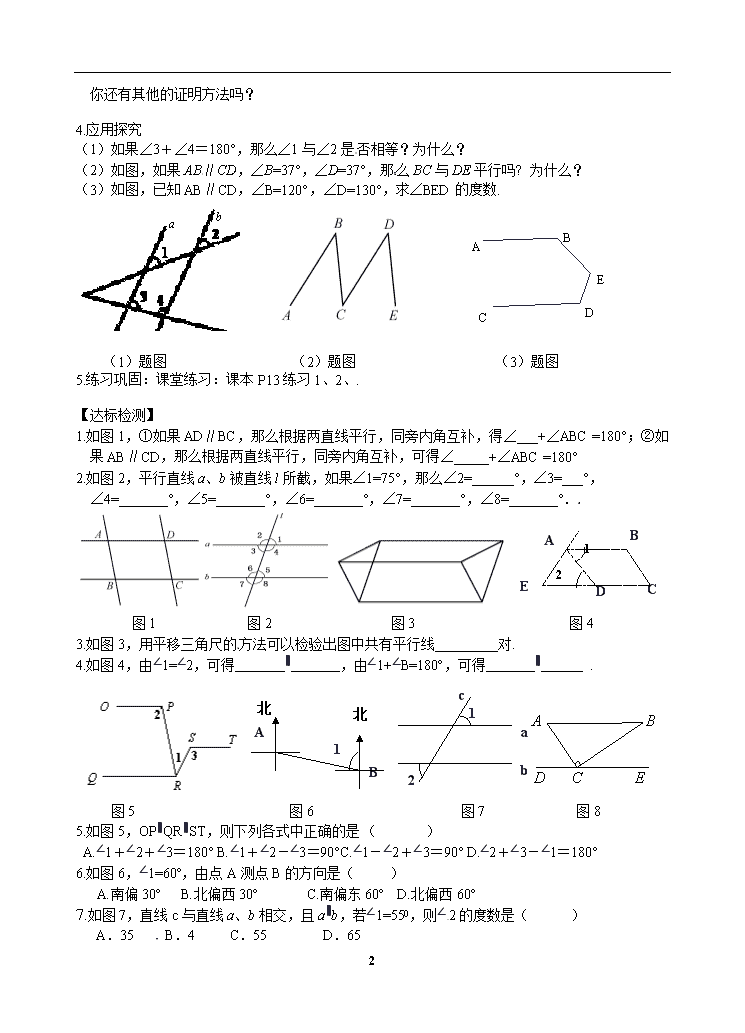‎ ‎4.应用探究 ‎（1）如果∠3＋∠4＝180°，那么∠1与∠2是否相等？为什么？‎ ‎（2）如图，如果AB∥CD，∠B=37°，∠D=37°，那么BC与DE平行吗? 为什么？‎ ‎（3）如图，已知AB∥CD，∠B=120°，∠D=130°，求∠BED的度数.‎ ‎ （1）题图 （2）题图 （3）题图 ‎5.练习巩固：课堂练习：课本P13练习1、2、.‎ ‎【达标检测】‎ ‎1.如图1，①如果AD∥BC，那么根据两直线平行，同旁内角互补，得∠___+∠ABC =180°；②如果AB∥CD，那么根据两直线平行，同旁内角互补，可得∠_____+∠ABC =180°‎ ‎2.如图2，平行直线a、b被直线l所截，如果∠1=75°，那么∠2=______°，∠3=___°，‎ ‎∠4=_______°，∠5=_______°，∠6=_______°，∠7=_______°，∠8=_______°．‎ E D C A B ‎1‎ ‎2‎ ‎ _‎ 图1 图2 图3 图4‎ ‎3.如图3，用平移三角尺的方法可以检验出图中共有平行线_________对.‎ ‎4.如图4，由∠1=∠2，可得 ∥ ，由∠1+∠B=180º，可得 ∥ .‎ ‎1‎ ‎2‎ a b c 北 A B ‎1‎ 北 ‎ 图5 图6 图7 图8‎ ‎5.如图5，OP∥QR∥ST，则下列各式中正确的是 （ ）‎ A.∠1＋∠2＋∠3＝180° B.∠1＋∠2－∠3＝90°C.∠1－∠2＋∠3＝90° D.∠2＋∠3－∠1＝180°‎ ‎6.如图6，∠1=60º，由点A测点B的方向是（ ）‎ ‎ A.南偏30º B.北偏西30º C.南偏东60º D.北偏西60º ‎ ‎7.如图7，直线c与直线a、b相交，且a∥b，若∠1=550，则∠2的度数是（　　　）‎ A．35 B．4 C．55 D．65 ‎ 4‎ ‎ ‎ ‎8.如图8，中，，过点且平行于，若，则的度数为（ ）A． B． C． D．‎ ‎【总结评价】‎内错角相等 ‎ 内错角相等 平行 同位角相等 ‎ 同旁内角互补 ‎【课后作业】课本P13习题7.2 1、2、3、4、5. 补充 ‎1.如图9，若，，则 ．‎ ‎2.如图10，把一张长方形纸条沿折叠，若，则 ． ‎ ‎1‎ A E D C F G B ‎3.如图11，，，则 ．‎ 图11‎ ‎1‎ ‎2‎ A B D C 图9 图10‎ ‎4.将一副三角板摆放成如图12所示，图中 度．‎ ‎5.如图13,直线AE∥CD,∠EBF=135°,∠BFD=60°,则∠D等于( )‎ ‎(A)75°. (B)45°. (C)30°. (D)15°.‎ ‎1‎ 图12‎ ‎ 图13‎ ‎ 图14‎ ‎6.已知，如图14，a∥b,c∥d,∠1=48°,‎ 求∠2，∠3，∠4的度数.‎ ‎7.在图（1）、图（2）图（3）、图（4）中，AB∥CD，说明∠A、∠E、∠C的等量关系.‎ 4‎ ‎ ‎ 图（1） 图（2） 图（3） 图（4）‎ 4‎