2017-2018学年山东省济南市天桥区七年级下期末考试数学试题含答案 13页

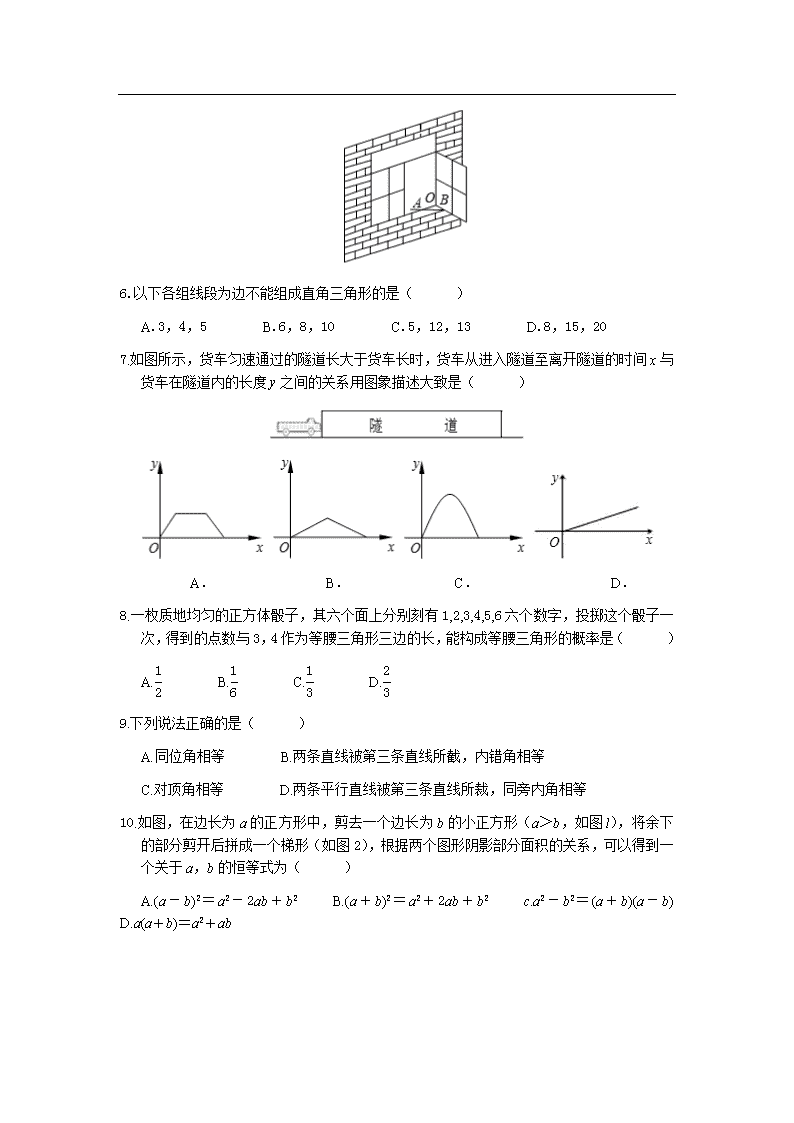
济南市天桥区 2017～2018 学年第二学期七年级下学期期末考试 数学试题 一、选择题（本大题共 12 小题，每小题 4 分，共 48 分） 1.下列标志中，可以看作是轴对称图形的是（ ） A． B． C． D． 2.济南春夏之季鲜花烂漫，空气中弥漫着各种花粉，有一种花粉的直径是 0.00006 3 米，将 0.000063 用科学记数法表示应为（ ） A．6.3×10－4 B.0.63×10－4 C.6.3×10－5 D.63×10－5 3.如图，直线 c 与直线 a，b 相交，且 a∥b，∠1＝60°，则∠2 的度数是（ ） A.30° B.60° C.80° D.120° 4.下列计算正确的是（ ） A.a5＋a2＝a3 B.2a2－a2＝2 C.a3·a2＝a6 D.(a3)3＝a6 5.如图，一扇窗户打开后，用窗钩 AB 可将其固定，这里所运用的几何原理是（ ） A.三角形的稳定性 B.两点之间钱段最短 C.两点确定一条直线 D.垂线段最短 b a c 2 1 6.以下各组线段为边不能组成直角三角形的是（ ） A.3，4，5 B.6，8，10 C.5，12，13 D.8，15，20 7.如图所示，货车匀速通过的隧道长大于货车长时，货车从进入隧道至离开隧道的时间 x 与 货车在隧道内的长度 y 之间的关系用图象描述大致是（ ） A． B． C． D． 8.一枚质地均匀的正方体骰子，其六个面上分别刻有 1,2,3,4,5,6 六个数字，投掷这个骰子一 次，得到的点数与 3，4 作为等腰三角形三边的长，能构成等腰三角形的概率是（ ） A. 1 2 B. 1 6 C. 1 3 D. 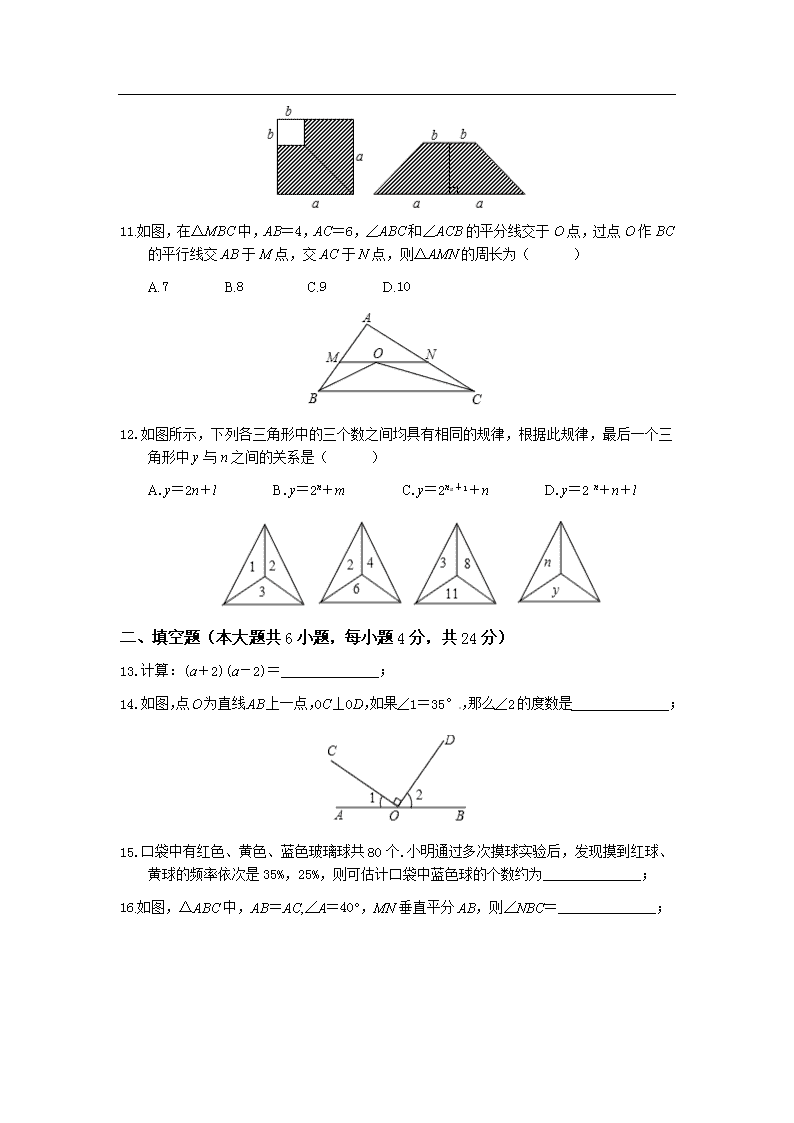2 3 9.下列说法正确的是（ ） A.同位角相等 B.两条直线被第三条直线所截，内错角相等 C.对顶角相等 D.两条平行直线被第三条直线所裁，同旁内角相等 10.如图，在边长为 a 的正方形中，剪去一个边长为 b 的小正方形（a＞b，如图 l），将余下 的部分剪开后拼成一个梯形（如图 2），根据两个图形阴影部分面积的关系，可以得到一 个关于 a，b 的恒等式为（ ） A.(a－ b) 2 ＝a 2 －2ab＋ b 2 B.(a＋b) 2 ＝a 2 ＋2ab＋ b 2 c.a2 －b 2 ＝(a ＋b)(a－b) D.a(a＋b)＝a2＋ab 11.如图，在△MBC 中，AB＝4，AC＝6，∠ABC 和∠ACB 的平分线交于 O 点，过点 O 作 BC 的平行线交 AB 于 M 点，交 AC 于 N 点，则△AMN 的周长为（ ） A.7 B.8 C.9 D.10 12.如图所示，下列各三角形中的三个数之间均具有相同的规律，根据此规律，最后一个三 角形中 y 与 n 之间的关系是（ ） A.y＝2n＋l B.y＝2n＋m C.y＝2n ＋1＋n D.y＝2 n＋n＋l 二、填空题（本大题共 6 小题，每小题 4 分，共 24 分） 13.计算：(a＋2)(a－2)＝______________； 14.如图，点O为直线AB上一点，0C⊥0D，如果∠1＝35° ，那么∠2的度数是______________； 15.口袋中有红色、黄色、蓝色玻璃球共 80 个.小明通过多次摸球实验后，发现摸到红球、 黄球的频率依次是 35%，25%，则可估计口袋中蓝色球的个数约为______________； 16.如图，△ABC 中，AB＝AC,∠A＝40°，MN 垂直平分 AB，则∠NBC＝______________； 17. 如 果 表 示 3xyz ， 表 示 一 2abcd ， 则 × ＝ ______________； 18.如图，在直线 l 上依 次摆放着七个正方形.已知斜放置的三个正方形的面积分别是 1，2， 3 ， 正 放 置 的 四 个 正 方 形 的 面 积 依 次 是 S1 ， S2 ， S3 ， S4 ， 则 S1 ＋ S2 ＋ S3 ＋ S4 ＝ ______________； 三、解答思（本大题 9 个小题，共 78 分，解答应写出文字说明、证明过程成演 算步现．） 19.（本小愿满分 6 分）计算： （1）2m(mn)2； (2)(－1)2018－(3.14－x)0＋2－1 20.（本小题满分 6 分）先化简，再求值： (a＋2)2－(a＋1)(a－1)，其中 a＝－ 3 2 z x y db a c n m 2 3 mn 2 21.（本小题满分 6 分）推理填空： 已知：如图，EF∥AD，∠1＝∠2，∠BAC＝70°.求∠AGD 的度数． 解：∵EF∥AD， ∴∠2＝______.(_____________________________) 又∵∠l＝∠2, ∴∠1＝∠3. ∴AB∥______.(_____________________________) ∴∠BAC＋______＝180°(_____________________________). 又∵∠BAC＝70°, ∴∠AGD＝______ . 22.（本小题满分 8 分） 如图，点 EF 在线段 AB 上，且 AD＝BC，∠A＝∠B，AE＝BF. 求证：DF＝CE. 32 1 E G B A C D F 23.（本小题满分 8 分） 如图，在正方形网格上有一个△ABC，三个顶点都在格点上，网格上的最小正方形的边 长为 1. （1）作△ABC 关于直线 MN 的对称图形△A′B′C′（不写作法）：I （2）求 BC 的长. （3）求△ABC 的面积。 24.（本小题满分 10 分） 小亮和小芳都想参加学校杜团组织的暑假实践活动，但只有一个名额，小亮提议用如下 的办法决定谁去等加活动：将一个转盘 9 等分，分别标上 1 至 9 九个号码，随意转动转盘， 若转到 2 的倍数，小亮去参加活动；转到 3 的倍数，小芳去参加活动；转到其它号码则重新 特动转盘． （1）转盘转到 2 的倍数的概率是多少？ （2）你认为这个游戏公平吗？请说明理由． C E BA F D C B A N M 25.（本小题满分 10 分） “龟免赛跑”的故事同学们都非常热悉，图中的线段 OD 和折线 OABC 表示“龟兔赛 跑时路程与时间的关系，请你根据图中给出的信息，解决下列问题. （1）填空：折线 OABC 表示赛跑过程中_______（填“兔子”或“乌龟”）的路程与时 间的关系，赛跑的全过程是___________米. （2）兔子在起初每分钟跑多少米?乌龟每分钟爬多少米？ （3）乌龟用了多少分钟追上了正在睡觉的兔子？ （4）兔子醒来假，以 400 米/分的速度跑向终点，结果还是比乌龟晚到了 0.5 分钟，请 你算算兔子中间停下睡觉用了多少分钟. 5 98 7 6 4 3 2 1 2 50 26（本小题满分 12 分） （1）同题情境：如图 1,AB∥CD，∠PAB＝130°，∠PCD＝120°.求∠APC 的度数.[来 源:Z#xx#k.Com] 小明想到一种方法，但是没有解答完： 如图 2，过 P 作 PE∥AB，∴∠APE＋∠PAB＝180°. ∴∠APE＝180°－∠PAB＝180°－130°＝50°. ∵AB∥CD.∴PE∥CD. ………… 请你帮助小明完成剩余的解答. （2）问题迁移：请你依据小明的思路，解答下面的问题： 如图 3，AD∥BC，点 P 在射线 OM 上运动，∠MDP＝∠α，∠BCP＝∠β. ①当点 P 在 A、B 两点之间时，∠CPD，∠α，∠β 之间有何数量关系？请说明理由. ②当点 P 在 A、B 两点外侧时（点 P 与点 O 不重合），请直接写出∠CPD，∠α，∠β 之间的数量关系. 27.（本小题满分 12 分） 如图 1，△ABC 为等边三角形，三角板的 60°角顶点与点 C 重合，三角板的一直角边 与 AB 交于点 D，在三角板斜边上取一点 F，使 CF＝CD，线段 AB 上取点 E，使∠DCE＝ 30°，连接 AF，EF. （1）求证：△ACF≌△BCD； （2）写出线段 DE 与 EF 之间的数量关系，并说明理由； （3）如图 2，若△ABC 为等腰直角三角形，∠ACB＝90°，三角板的 90°角顶点与点 C 重合，三角板的一直角边与 AB 交于点 D，在三角板另一直角边上取一点 F，使 CF＝CD， 在线段 AB 上取点 E，使∠DCE＝45°，连接 AF，EF.请写出三条线段 AE，ED，DB 之间 的数量关系，并说明理由.[来源:学科网 ZXXK] 2017～2018 学年度第二学期七年级期末考试试题答案 一、 选择题 1．D 2．C 3．B 4．A 5．A 6．D 7．A 8．C 9．C 10．C 11．D 12．B 二、填空题 13. 14.550 15．32 16.300 17． 18 ．4 19. （1） (2)解： 2 4a − 4 312m n− ( )22m mn 2 22m m n=  3 22m n= ( ) ( )2018 0 11 3.14 2π −− − − + 20.解: (a＋2)2－(a＋1)(a－1) ＝a2＋4a＋4－a2＋1＝4a＋5. 当 a＝－ 3 2时，原式＝4×(－ 3 2)＋5＝－1. 21. 解：∵E F∥AD， ∴∠2＝∠3．( 两直线平行，同位角相等)， 又∵∠1＝∠2， ∴∠1＝∠3，[来源:学,科,网] ∴AB∥DG( 内错角相等，两直线平行)， ∴∠BAC＋∠AGD ＝180°． 又∵∠BAC＝70°， ∴∠AGD＝1100 22.证明：证明：∵点 E，F 在线段 AB 上，AE＝B F.， ∴AE＋EF＝BF＋EF， 即：AF＝BE． 在△ADF 与△BCE 中，[来源:学+科+网] ∴△ADF≌△BCE(SAS) ∴ DF＝CE（全等三角形对应边相等） 23. （1）作图 （2）解：在网格中构建 Rt△BCD, ∵在 Rt△BCD 中，BD＝4，CD＝3∴BD2＋CD2＝BC2 ∴42＋32＝BC2 11 1 2 = − + 1 2 = , , , AD BC A B AF BE = ∠ = ∠  = 第 22 题图 A B CD E F AB C D G E F 1 2 3 第 21 题图 M N A B CD Aˊ B ˊ Cˊ BC＝5 （3）解： 24. 解：（1）∵共有 9 种等可能的结果， 其中 2 的倍数有 4 个 ∴P（转到 2 的倍数）＝ － （2）游戏不公平∵共有 9 种等可能的结果， 其中 3 的倍数有 3 个， ∴P（转到 3 的倍数）＝ ＝ ∵ ＞ ∴游戏不公平 25.解：（ ）兔子 （ ）结合图象得出： 兔子在起初每分钟跑 （米），乌龟每分钟爬 （米）． （ ） （分钟）， 所以乌龟用了 分钟追上了正在睡觉的兔子． （ ） （分钟）， （分钟）， 所以兔子中间停下睡觉用了 分钟． 26.解：（1）剩余过程：∴∠CPE＋∠PCD＝1800， ∴∠CPE＝1800—1200＝600∴∠APC＝500＋600＝1100 1 1 13 5 1 2 1 5 3 42 2 2 × − × × − × × − × × 4 9 3 9 1 3 4 9 1 3 1 1500 2 700 2 350÷ = 1500 50 30÷ = 3 70700 30 3 ÷ = 70 3 4 (1500 700) 400 2− ÷ = 50 0.5 2 2 46.5+ − − = 46.5 515 1 62 = − − − 11 2 = 1 2 3 456 7 8 9 第 24 题 图 （2）①过 P 作 PQ∥AD [来源:学.科.网 Z.X.X.K] ∵ AD∥BC，∴PQ∥BC ，∴ 同理， ∴ （2）②当点 P 在 B、O 两点之间时， ； 当点 P 在射线 AM 上时， 27. 解：（1）∵△ABC 是等边三角形，∴AC＝BC，∠BAC＝∠B＝∠BCA ＝60°， ∵∠DCF＝60°，∴∠ACF＝∠BCD 在△ACF 和△BCD 中， ，∴△ACF≌△BCD（SAS）， (2)DE＝EF； 理由如下： ∵∠DCF＝60°，∠DCE＝30°，∴∠FCE＝60°﹣30°＝30°， ∴∠DCE＝∠FCE，在△DCE 和△FCE 中， ， ∴△DC E≌△FCE（SAS）， ∴DE＝E F； （3）AE2＋DB2＝DE2，理由如下： ∵△ABC 是等腰直角三角形，∠ACB＝90°， ∴AC＝BC，∠BAC＝∠B＝45°， ∵∠DCF＝90°，∴∠ACF＝∠BCD， βα 21 Q B N O M D A C P Q B N O M D A C P Q B N O M D A C P 1α∠ = ∠ 2β∠ = ∠ 1 2CPD α β∠ = ∠ + ∠ = ∠ + ∠ CPD α β∠ = ∠ − ∠ CPD β α∠ = ∠ − ∠ ∵CF＝CD，∴△ACF≌△BCD（SAS）， ∴∠CAF＝∠B＝45°，AF＝DB，∴∠EAF＝∠BAC＋∠CAF＝90°； ∵∠DCF＝90°，∠DCE＝45°，∴∠FCE＝90°﹣45°＝45°，∴∠DCE＝∠FCE， 在△DCE 和△FCE 中， ，∴△DCE≌△FCE（SAS），∴DE＝EF， 在 Rt△AEF 中，AE2＋AF2＝EF2， 又∵AF＝DB，∴AE2＋DB2＝DE2．