人教版七年级数学下册同步练习与单元检测题+数学下册教学计划表大全集 42页

人教版七年级数学下册同步练习与单元检测题+数学下册教学计划表大全集七下数学单元检测同步练习第五章相交线与平行线一、知识结构邻补角：两条直线相交所构成的四个角中，有公共顶点且有一条公共边的两个角是邻补角。对顶角：有一个公共端点一个角的两边是另一个角两边的反向延长线线。对顶角性质：对顶角相等。垂线：1.当两直线相交，有一个夹角为90°时这两条直线垂直.a⊥b读做a垂直于b垂足为O2.两直线相交构成四个夹角相等，两直线互相垂直。其中一条直线叫做另一条直线的垂线。垂直性质1：过一点有且仅有一条直线，与以已知直线垂直。垂直性质2：连接直线外一点与直线上各点的所有线段中，垂线段最短。平行线定义：在同一平面内永不相交的两条直线。记作a∥b读作：a平行于b平行线公理：1.经过直线外一点，有且只有一条直线于已知直线平行。2.如果两条直线都与第三条直线平行，那么这两条直线也互相平行平行判定方法:1.同位角相等，两直线平行。如果∠1=∠2那么a∥b2.内错角相等，两直线平行如果∠2=∠3那么a∥b3.同旁内角互补，两直线平行。∠A+∠B=180°那么两直线平行。平行线的性质：1.两直线平行，同位角相等。∵a∥b∴∠1=∠22.两直线平行，内错角相等。∵a∥b∴∠3=∠43.两直线平行，同位角互补∵a∥b∴∠3+∠4=180°命题：判断一件事情的语句。1.命题的结构，命题由题设（已知事项或条件）推出的结论（由已知事项推出的事项）2.任何命题都可以改写成如果那么的形式，如果后面引导题设，那么后面引导结论。真命题：题设成立，结论成立假命题：题设成立，结论不成立两点之间的距离：连接两点的线段的长度叫做两点间的距离。两条平行线间的距离：同时垂直于两条平行线，并且夹在这两条平行线间的垂线段，叫做这两条平行线的距离。平行线间的距离，处处相等。平移：在平面内，将一个图形沿某个方向移动一定的距离，图形的这种移动叫做平移平移变换，简称平移。.平移不改变物体的大小.平移前后对应点的直线相等：且互相平行。对应点：平移后得到的新图形中每一点，都是由原图形中的某一点移动后得到的，这样的两个点叫做对应点。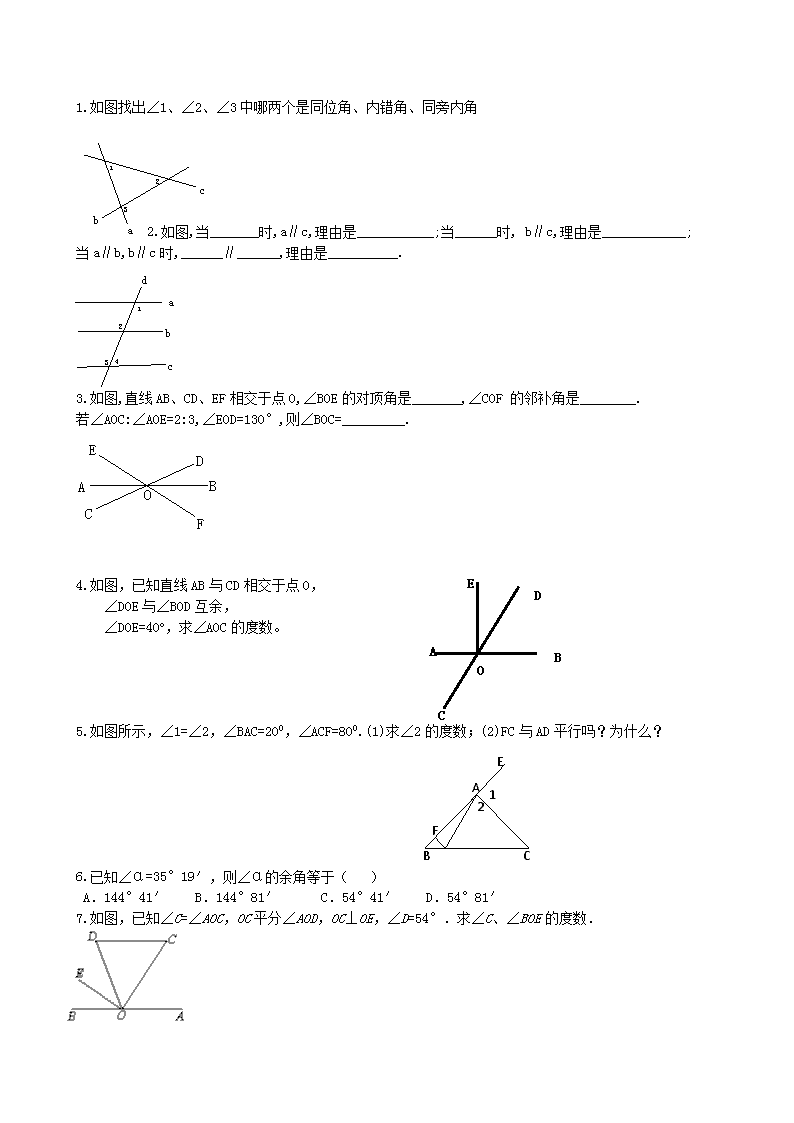二、练习 1.如图找出∠1、∠2、∠3中哪两个是同位角、内错角、同旁内角2.如图,当_______时,a∥c,理由是___________;当______时,b∥c,理由是____________;当a∥b,b∥c时,______∥______,理由是__________.3.如图,直线AB、CD、EF相交于点O,∠BOE的对顶角是_______,∠COF的邻补角是________.若∠AOC:∠AOE=2:3,∠EOD=130°,则∠BOC=_________.ED4.如图，已知直线AB与CD相交于点O，∠DOE与∠BOD互余，A∠DOE=40o，求∠AOC的度数。BOC5.如图所示，∠1=∠2，∠BAC=200，∠ACF=800.(1)求∠2的度数；(2)FC与AD平行吗？为什么？ABCDEF126.已知∠α=35°19′，则∠α的余角等于（）A．144°41′B．144°81′C．54°41′D．54°81′7.如图，已知∠C=∠AOC，OC平分∠AOD，OC⊥OE，∠D=54°．求∠C、∠BOE的度数． 8.如图，一条公路修到湖边时，需拐弯绕湖而过；如果第一次拐的角∠A是120○，第二次拐的角∠B是150○，第三次拐的角是∠C，这时的道路恰好和第一次拐弯之前的道路平行，则∠C是．9.如图1，直线AB、CD相交于点O，∠1＝∠2．则∠1的对顶角是_____，∠4的邻补角是______．∠2的补角是_________．图2图1图310.如图2，OA⊥OB，OC⊥OD．若∠AOD＝144°，则∠BOC＝_____．11.如图3，∠1＝82°，∠2＝98°，∠3＝80°，则∠4＝．12.如图，已知：AB∥CD，∠1=55°∠2=80°，求∠3的度数．13.如图，已知：AB∥CD，BE∥CF．求证：∠1=∠4．14.如图所示，已知∠OEB=130°，∠FOD=25°，OF平分∠EOD，试说明AB∥CD．15.下列语句是命题的个数为（）①画∠AOB的平分线;②直角都相等;③同旁内角互补吗？④若│a│=3，则a=3.A．1个B．2个C．3个D．4个16.将下列命题改写成“如果……那么……”的形式．（1）直角都相等． （2）末位数是5的整数能被5整除．（3）三角形的内角和是180°．（4）平行于同一条直线的两条直线互相平行．17.如图所示，经过平移，四边形ABCD的顶点A移到点A′，作出平移后的四边形．相交线与平行线能力测试题一、选择题。1、如图点E在AC延长线上，下列条件中能判断AB∥CD的是（）A、∠3=∠4B、∠1=∠2C、∠D=∠DCED、∠D+∠ACD=18002、如图a∥b，∠3=1080，则∠1的度数是（）A、720B、800C、820D、10803、下列说法正确的是（）A、a、b、c是直线，且a∥b,b∥c,则a∥cB、a、b、c是直线，且a⊥b,b⊥c，则a⊥cC、a、b、c是直线，且a∥b,b⊥c则a∥cD、a、b、c是直线，且a∥b,b∥c，则a⊥c4、如图由AB∥CD，可以得到（）A、∠1=∠2B、∠2=∠3C、∠1=∠4D、∠3=∠45、如图B∥CD∥EF，那么∠BAC+∠ACE+∠CEF=（）A、1800B、2700C、3600D、54006、下列命题中，错误的是（）A、邻补角是互补的角B、互补的角若相等，则此两角是直角C、两个锐角的和是锐角D、一个角的两个邻补角是对顶角7、图中，与∠1成同位角的个数是（）A、2个Ｂ、３个Ｃ、４个Ｄ、５个二、填空题。８、如图一个弯形管道ＡＢＣＤ的拐角∠ＡＢＣ＝１２０0，∠ＢＣＤ＝６０0，这时说管道ＡＢ∥ＣＤ，是根据９、如图直线ＡＢ、ＣＤ、ＥＦ相交于点Ｏ，是∠ＡＯＣ的邻补角是，∠ＤＯＡ的对顶角是，若∠ＡＯＣ＝５０0，则 ∠ＢＯＤ＝0，∠ＣＯＢ＝010、如图所示的长方体，用符号表示下列棱的位置关系：A1B1ABAA1AB1，A1D1C1D1ADBC11、如图直线，a∥b,∠1=540，则∠2=0，∠3=0，∠4=0。12、命题“同角的余角相等”的题设是，结论是。13、如图OC⊥AB，DO⊥OE，图中与∠1与互余的角是，若∠COD=600，则∠AOE=0。14、如图直线AB分别交直线EF，CD于点M，N只需添一个条件就可得到EF∥CD。三、解答题15、推理填空：（12分）如图①若∠1=∠2则∥（）若∠DAB+∠ABC=1800则∥（）②当∥时∠C+∠ABC=1800（）当∥时∠3=∠C（）16．已知，如图，　　（１５分）试说明：解：∵　∠ＢＡＥ＋∠ＡＥＤ＝１８００（　　　　　）　　∴　　　　（）　　　　　　∴　∠ＢＡＥ＝　　　　　（　　　　　　　　）又　∵　∠Ｍ＝∠Ｎ　　　　　（　　　　　　　　）∴　　　　　∥　　　　　（　　　　　　　　）　　∴　∠ＭＡＥ＝　　　　　（　　　　　　　　）　　∴　∠ＢＡＥ－∠ＭＡＥ＝　　　　－　　　　　即　∠１＝∠２（）17、已知：如图ＡＢ∥ＣＤ，ＥＦ交ＡB于G，交CD于F，FH平分∠EFD，交AB于H，∠AGE=500求：∠BHF的度数。 18、如图，∠1=300，∠B=600，AB⊥AC①∠DAB+∠B=0②AD与BC平行吗？AB与CD平行吗？试说明理由。19、（10分）已知：如图AE⊥BC于点E，∠DCA=∠CAE，试说明CD⊥BC20、已知：如图∠1=∠2，∠C=∠D，∠A=∠F相等吗？试说明理由第五章达标测试1．下列所示的四个图形中，和是同位角的是（）A.②③B.①②③C.①②④D.①④2．如右图所示，点在的延长线上，下列条件中能判断（）A.B.C.D.3．一学员练习驾驶汽车，两次拐弯后，行驶的方向与原来的方向相同，这两次拐弯的角度可能是（）A.第一次向左拐，第二次向右拐B.第一次向右拐，第二次向左拐C.第一次向右拐，第二次向右拐D.第一次向左拐，第二次向左拐 4．两条平行直线被第三条直线所截，下列命题中正确的是（）A.同位角相等，但内错角不相等B.同位角不相等，但同旁内角互补C.内错角相等，且同旁内角不互补D.同位角相等，且同旁内角互补5．下列说法中错误的个数是（）（1）过一点有且只有一条直线与已知直线平行。（2）过一点有且只有一条直线与已知直线垂直。（3）在同一平面内，两条直线的位置关系只有相交、平行两种。（4）不相交的两条直线叫做平行线。（5）有公共顶点且有一条公共边的两个角互为邻补角。A.1个B.2个C.3个D.4个6．下列说法中，正确的是（）A.图形的平移是指把图形沿水平方向移动。B.平移前后图形的形状和大小都没有发生改变。C.“相等的角是对顶角”是一个真命题。D.“直角都相等”是一个假命题。7．如右图，，且，，则的度数是（）A.B.C.D.8．邻补角是（）A.和为180°的两个角B.有公共顶点且互补的两个角C.有一条公共边且相等的两个角D.有公共顶点且有一条公共边，另一边互为反向延长线的两个角9．在一个平面内，任意四条直线相交，交点的个数最多有（）A.7个B.6个C.5个D.4个10.如右图所示，平分，，图中相等的角共有（）A.3对B.4对C.5对D.6对二、填空题1．把命题“等角的余角相等”写成“如果……，那么……。”的形式为2．用吸管吸易拉罐内的饮料时，如图①，，则（拉罐的上下底面互相平行）3．有一个与地面成30°角的斜坡，如图②，现要在斜坡上竖一电线杆，当电线杆与斜坡成的°时，电线杆与地面垂直。4．如图③，按角的位置关系填空：与是；与是；与是。 5．如图④，若，则。6.如图⑤，已知，若，则；若，则。7．如图⑥，为了把平移得到，可以先将向右平移格，再向上平移格。8．已知直线在同一平面，若，，则。9．三条直线、、相交于点，如图⑦所示，的对顶角是，的对顶角是，的邻补角是。三、解答题。1．如图，已知，，,求和的度数。2．如图，已知：，，求的度数。3．如图，已知，，求证：。4．如图，，平分，与相交于,。求证：。 5．如图，已知，，是的平分线，，求的度数。第五章单元测试卷一.选择题。1.邻补角是（）A.和为180°的两个角B.有公共顶点且互补的两个角C.有一条公共边且相等的两个角D.有公共顶点且有一条公共边，另一边互为反向延长线的两个角 2．下图中，∠1和∠2是同位角的是()                        A．            B．          C．          D．3.如图4，直线AB、CD相交于点O，OE⊥AB于O，若∠COE=55°，则∠BOD的度数为（）A.40°B.45°C.30°D.35°4.如图5，已知ON⊥l,OM⊥l,所以OM与ON重合，其理由是（）A.过两点只有一条直线B.经过一点有且只有一条直线垂直于已知直线C.垂线段最短D.过一点只能作一条垂线5．如图（1）所示，同位角共有（   ） 　　　　　A．1对        B．2对        C．3对    D．4对6.如图6，属于内错角的是（）A.∠1和∠2B.∠2和∠3C.∠1和∠4D.∠3和∠47．一辆汽车在笔直的公路上行驶，两次拐弯后，仍在原来的方向上平行前进，则两次拐弯的角度可以是（   ）A．第一次向右拐40°，第二次向左拐140°B．第一次向左拐40°，第二次向右拐40°C．第一次向左拐40°，第二次向右拐140°D．第一次向右拐40°，第二次向右拐40° 8．如图（2）所示，∥，AB⊥，∠ABC=130°，那么∠α的度数为（　　）　　　　　　A．60°    B．50°   C．40°   D．30° 9．适合的△ABC是（   ）    A．锐角三角形   B．直角三角形   C．钝角三角形   D．不能确定10.在下列实例中，不属于平移过程的有（）个。⑴时针运转过程；⑵火箭升空过程；⑶地球自转过程；⑷飞机从起跑到离开地面的过程。A.1B.2C.3D.4二，填空题。1.如图1，直线AB、CD相交于点O，已知∠AOC+∠BOD=90°，则∠BOC=。2.在无风的情况下，一个重物从高空落入池塘，它的运动路线与水面的关系是。3.如图2，所示直线AB、CD被直线EF所截，⑴量得∠1=80°，∠2=80°，则判定AB∥CD，根据是；⑵量得∠3=100°，∠4=100°，也判定AB∥CD，根据是。4.如图3，AB∥DE，BC∥FE，则∠E+∠B=。5.命题“两直线平行，内错角相等”的题设是，结论是；命题“内错角相等，两直线平行”的题设是，结论是。三.将以下各推理过程的理由填入括号内。1.如图7，∠B=∠C，AB∥EF试说明：∠BGF=∠C答：因为∠B=∠C所以AB∥CD（）又因为AB∥EF所以EF∥CD（）所以∠BGF=∠C（）2.如图8，AD⊥BC于D，EG⊥BC于G，∠E=∠3试说明：AD平分∠BAC答：因为AD⊥BC，EG⊥BC所以AD∥EG（）所以∠1=∠E（） ∠2=∠3（）又因为∠3=∠E所以∠1=∠2所以AD平分∠BAC（）四.平移作图。1.将图9中的图案向右平移4cm。五.把下列命题改写成“如果……，那么……”的形式。1.线段，则。2.在同一平面内，若a⊥b,c⊥b,则a∥c六.解答题。1.如图10，直线AB、CD相交于点O，若∠BOC比∠AOC的2倍多33°，求∠BOC、∠BOD的度数。2.如图11，直线MN与直线AB、CD相交于M、N，∠3=∠4，试说明∠1=∠2。3.如图12，已知AC⊥AE，BD⊥BF，∠1=35°，∠2=35°，AC与BD平行吗？AE与BF平行吗？为什么？4.已知：如图13，AB∥CD，求∠A+∠E+∠C的度数。（12分） 5.如图14，已知CE∥DF，求∠ACE+∠ABD-∠CAB的度数。（14分）第六章平面直角坐标系一、知识定义有序数对：有顺序的两个数a与b组成的数对叫做有序数对，记做（a,b）平面直角坐标系：在平面内，两条互相垂直且有公共原点的数轴组成平面直角坐标系。横轴、纵轴、原点：水平的数轴称为x轴或横轴；竖直的数轴称为y轴或纵轴；两坐标轴的交点为平面直角坐标系的原点。坐标：对于平面内任一点P，过P分别向x轴，y轴作垂线，垂足分别在x轴，y轴上，对应的数a,b分别叫点P的横坐标和纵坐标。象限：两条坐标轴把平面分成四个部分，右上部分叫第一象限，按逆时针方向一次叫第二象限、第三象限、第四象限。坐标轴上的点不在任何一个象限内。二、经典例题例1一个机器人从O点出发，向正东方向走3米到达A1点，再向正北方向走6米到达A2点，再向正西方向走9米到达A3点，再向正南方向走12米到达A4点，再向正东方向走15米到达A5点，如果A1求坐标为（3，0），求点A5的坐标。 例2如图是在方格纸上画出的小旗图案，若用(0，0)表示A点，(0，4)表示B点，那么C点的位置可表示为()ABC例2A、(0，3)B、(2，3)C、(3，2)D、(3，0)例3如图，面积为12cm2的△ABC向x轴正方向平移至△DEF的位置，相应的坐标如图所示（a，b为常数），（1）、求点D、E的坐标（2）、求四边形ACED的面积。例4过两点A（3，4）,B（-2，4）作直线AB，则直线AB()A、经过原点B、平行于y轴C、平行于x轴D、以上说法都不对第六章平面直角坐标系基础训练题一、填空题1、原点O的坐标是，x轴上的点的坐标的特点是，y轴上的点的坐标的特点是；点M（a，0）在轴上。2、点A（﹣1，2）关于轴的对称点坐标是；点A关于原点的对称点的坐标是。点A关于x轴对称的点的坐标为3、已知点M与点N关于轴对称，则。4、已知点P与点Q关于轴对称，则。5、点P到x轴的距离是2，到y轴的距离是3，则P点的坐标是。6、线段CD是由线段AB平移得到的。点A（–1，4）的对应点为C（4，7），则点B（–4，–1）的对应点D的坐标为______________。7、在平面直角坐标系内，把点P（－5，－2）先向左平移2个单位长度，再向上平移4个单位长度后得到的点的坐标是。 8、将点P(-3，y)向下平移3个单位，向左平移2个单位后得到点Q(x，-1)，则xy=___________。9、已知AB∥x轴，A点的坐标为（3，2），并且AB＝5，则B的坐标为。10、A（–3，–2）、B（2，–2）、C（–2，1）、D（3，1）是坐标平面内的四个点，则线段AB与CD的关系是_________________。11、在平面直角坐标系内，有一条直线PQ平行于y轴，已知直线PQ上有两个点，坐标分别为（－a，－2）和（3，6），则。12、点A在x轴上，位于原点左侧，距离坐标原点7个单位长度，则此点的坐标为；13、在Y轴上且到点A（0，－3）的线段长度是4的点B的坐标为___________________。14、在坐标系内，点P（2，－2）和点Q（2，4）之间的距离等于个单位长度。线段PQ的中点的坐标是________________。15、已知P点坐标为（2－a，3a＋6），且点P到两坐标轴的距离相等，则点P的坐标是_________________________________________________。16、已知点A（－3+a，2a+9）在第二象限的角平分线上，则a的值是____________。17、已知点P（x，－y）在第一、三象限的角平分线上，由x与y的关系是_____________。18、若点B(a，b)在第三象限，则点C(－a+1，3b－5)在第____________象限。19、如果点M（x+3，2x－4）在第四象限内，那么x的取值范围是______________。20、已知点P在第二象限，且横坐标与纵坐标的和为1，试写出一个符合条件的点P。点K在第三象限，且横坐标与纵坐标的积为8，写出两个符合条件的点。21、已知点A（a，0）和点B（0，5）两点，且直线AB与坐标轴围成的三角形的面积等于10，则a的值是________________。22、已知，则点（，）在。二、选择题1、在平面直角坐标系中，点一定在（　　）A、第一象限　　　B、第二象限　　　C、第三象限　　D、第四象限2、如果点A（a.b）在第三象限，则点B（－a+1,3b－5）关于原点的对称点是（）A第一象限B第二象限C第三象限D第四象限3、点P（a，b）在第二象限，则点Q(a-１，b+1)在()　　（A）第一象限（B）第二象限（C）第三象限(D)第四象限4、若，且点M（a，b）在第二象限，则点M的坐标是（）A、（5，4）B、（－5，4）C、（－5，－4）D、（5，－4）5、△DEF（三角形）是由△ABC平移得到的，点A（－1，－4）的对应点为D（1，－1），则点B（1，1）的对应点E、点C（－1，4）的对应点F的坐标分别为（）A、（2,2），（3,4）B、（3,4）,(1,7)C、（－2,2），（1,7）D、（3,4），（2,－2）6、过A（4，－2）和B（－2，－2）两点的直线一定（）A．垂直于x轴B．与Y轴相交但不平于x轴C．平行于x轴D．与x轴、y轴平行7、已知点A在轴上方，轴的左边，则点A到轴、轴的距离分别为（　　）A、　B、C、　D、8、一个长方形在平面直角坐标系中三个顶点的坐标为（–1，–1）、（–1，2）、（3，–1），则第四个顶点的坐标为（）A．（2，2）B．（3，2）C．（3，3）D．（2，3）9、若x轴上的点P到y轴的距离为3，则点P的坐标为（）A．（3，0）B．（3，0）或（–3，0）C．（0，3）D．（0，3）或（0，–3）10、在直角坐标系内顺次连结下列各点，不能得到正方形的是（）A、(-2，2)（2，2）(2，-2)(-2，-2)；B、(0，0)(2，0)(2，2)(0，2)；C、(0，0)(0，2)(2，-2)(-2，0)；D、(-1，-1)(-1，1)(1，1)(1，-1)。 11、已知三角形的三个顶点坐标分别是（-1，4），（1，1），（-4，-1），现将这三个点先向右平移2个单位长度，再向上平移3个单位长度，则平移后三个顶点的坐标是（）A、（-2，2），（3，4），（1，7）；B、（-2，2），（4，3），（1，7）；C、（2，2），（3，4），（1，7）；D、（2，-2），（3，3），（1，7）12、在平面直角坐标系中,将三角形各点的纵坐标都减去3,横坐标保持不变,所得图形与原图形相比（）A.向右平移了3个单位B.向左平移了3个单位C.向上平移了3个单位D.向下平移了3个单位13、若点P(,)在第二象限，则下列关系正确的是（）ABCD三、解答题1、在图所示的平面直角坐标系中表示下面各点:A（0，3）；B（1，-3）；C（3，-5）；D（-3，-5）；E（3，5）；F（5，7）；G（5，0）（1）A点到原点O的距离是。（2）将点C向轴的负方向平移6个单位，它与点重合。（3）连接CE，则直线CE与轴是什么关系？（4）点F分别到、轴的距离是多少？2、如图所示的直角坐标系中，三角形ABC的顶点坐标分别是A（0,0），B（6,0），C（5,5）。（1）求三角形ABC的面积；（2）如果将三角形ABC向上平移1个单位长度，得三角形A1B1C1，再向右平移2个单位长度，得到三角形A2B2C2。试求出A2、B2、C2的坐标；（3）三角形A2B2C2与三角形ABC的大小、形状有什ACAXAYBA么关系。3、如图，在平面直角坐标系中，第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3。（1）观察每次变换前后的三角形的变化规律，若将△OA3B3变换成△OA4B4,则A4的坐标是＿＿＿，B4的坐标是＿＿＿＿。 （2）若按第（1）题找到的规律将△OAB进行n次变换，得到△OAnBn，比较每次变换中三角形顶点坐标有何变化，找出规律，推测An的坐标是＿＿＿＿，Bn的坐标是＿＿＿＿＿。第七章三角形一、知识定义三角形：由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。三边关系：三角形任意两边的和大于第三边，任意两边的差小于第三边。高：从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足间的线段叫做三角形的高。中线：在三角形中，连接一个顶点和它的对边中点的线段叫做三角形的中线。角平分线：三角形的一个内角的平分线与这个角的对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线。三角形的稳定性：三角形的形状是固定的，三角形的这个性质叫三角形的稳定性。多边形：在平面内，由一些线段首尾顺次相接组成的图形叫做多边形。多边形的内角：多边形相邻两边组成的角叫做它的内角。多边形的外角：多边形的一边与它的邻边的延长线组成的角叫做多边形的外角。多边形的对角线：连接多边形不相邻的两个顶点的线段，叫做多边形的对角线。正多边形：在平面内，各个角都相等，各条边都相等的多边形叫做正多边形。平面镶嵌：用一些不重叠摆放的多边形把平面的一部分完全覆盖，叫做用多边形覆盖平面。三角形的内角和：三角形的内角和为180° 三角形外角的性质：性质1：三角形的一个外角等于和它不相邻的两个内角的和。性质2：三角形的一个外角大于任何一个和它不相邻的内角。多边形内角和公式：n边形的内角和等于（n-2）·180°多边形的角和：多边形的外角和为360°。多边形对角线的条数：（1）从n边形的一个顶点出发可以引（n-3）条对角线，把多边形分词（n-2）个三角形。（2）n边形共有条对角线。七年级数学第七章三角形复习训练题一、填空题1.锐角三角形的三条高都在，钝角三角形有条高在三角形外，直角三角形有两条高恰是它的。2.若等腰三角形的两边长分别为3cm和8cm，则它的周长是。3.要使六边形木架不变形，至少要再钉上根木条。4.在△ABC中，若∠A=∠C=∠B，则∠A=，∠B=，这个三角形是。5、三角形有两条边的长度分别是5和7，则第三条边的取值范围是___________。6、△ABC中，∠A＝50°，∠B＝60°，则∠C＝。7、将一个三角形截去一个角后，所形成的一个新的多边形的内角和___________。8、等腰三角形的底边长为10cm,一腰上的中线将这个三角形分成两部分,这两部分的周长之差为2cm,则这个等腰三角形的腰长为_____________________.9、古希腊数学家把数1，3，6，10，15，21，…，叫做三角形数，它有一定的规律性，则第24个三角形数与第22个三角形数的差为．10、在ABC中，如果∠B－∠A－∠C=50°，∠B=____________。11、一个多边形的内角和是1980°，则它的边数是____，共有条对角线____，它的外角和是____。12、观察下图，我们可以发现：图⑴中有1个正方形；图⑵中有5个正方形，图⑶中共有14个正方形，按照这种规律继续下去，图⑹中共有_______个正方形。二、选择题1、小芳画一个有两边长分别为5和6的等腰三角形，则它的周长是（）A、16B、17C、11D、16或172、如图，已知直线AB∥CD，当点E直线AB与CD之间时，有∠BED＝ ABECD∠ABE＋∠CDE成立；而当点E在直线AB与CD之外时，下列关系式成立的是（　　　）　A　∠BED＝∠ABE＋∠CDE或∠BED＝∠ABE－∠CDE　B　∠BED＝∠ABE－∠CDE　C　∠BED＝∠CDE－∠ABE或∠BED＝∠ABE－∠CDE　D　∠BED＝∠CDE－∠ABE　3、以长为3cm，5cm，7cm，10cm的四根木棍中的三根木棍为边，可以构成三角形的个数是（）A．1个B．2个C．3个D．4个4、已知一多边形的每一个内角都等于150°，则这个多边形是正（）DABECP(A)十二边形(B)十边形(C)八边形(D)六边形5、边长相等的下列两种正多边形的组合，不能作平面镶嵌的是(　)　　A.正方形与正三角形　　　B.正五边形与正三角形　　C.正六边形与正三角形　　D.正八边形与正方形6、如图，在锐角△ABC中，CD、BE分别是AB、AC边上的高，且相交于一点P，若∠A=50°，则∠BPC的度数是（）A．150°B．130°C．120°D．100°7、中华人民共和国国旗上的五角星，它的五个锐角的度数和是（）A、500B、1000C、1800D、20008、在ABC中，三个内角满足∠B－∠A=∠C－∠B，则∠B等于（）A、70°B、60°C、90°D、120°9、在锐角三角形中，最大内角的取值范围是（）A、0°＜＜90°B、60°＜＜180°C、60°＜＜90°D、60°≤＜90°10、下面说法正确的是个数有（　　）①如果三角形三个内角的比是１∶２∶３，那么这个三角形是直角三角形；②如果三角形的一个外角等于与它相邻的一个内角，则这么三角形是直角三角形；③如果一个三角形的三条高的交点恰好是三角形的一个顶点，那么这个三角形是直角三角形；④如果∠A=∠B=∠C，那么△ABC是直角三角形；⑤若三角形的一个内角等于另两个内角之差，那么这个三角形是直角三角形；⑥在ABC中，若∠A＋∠B=∠C，则此三角形是直角三角形。A、3个B、4个C、5个D、5个11、在ABC中，的平分线相交于点P，设用x的代数式表示的度数，正确的是（　　）（A）（B）（C）（D）12、探究规律：如图，已知直线∥，A、B为直线上的两点，C、P为直线上的两点。（1）请写出图中面积相等的各对三角形：______________________________。（2）如果A、B、C为三个定点，点P在上移动，那么无论P点移动到任何位置总有：与△ABC的面积相等；nmOBAPC理由是： 13、如图,在△ABC中,AD⊥BC,CE是△ABC的角平分线,AD、CE交于F点.当∠BAC=80°,∠B=40°时,求∠ACB、∠AEC、∠AFE的度数.第13题图14、如图，在直角三角形ABC中，∠ACB=90°，CD是AB边上的高，AB=13cm，BC=12cm，AC=5cm，求:(1)△ABC的面积；(2)CD的长；（3）作出△ABC的边AC上的中线BE，并求出△ABE的面积；（4）作出△BCD的边BC边上的高DF，当BD=11cm时，试求出DF的长。七年级数学第七章三角形测试题一、填空题（每空2分，共30分）1、在直角三角形、钝角三角形和锐角三角形这三种三角形中，有两条高在三角形外部的是三角形。2、如图1，AD是△ABC的中线，如果△ABC的面积是18cm2,则△ADC的面积是______________cm2。3、把一副常用的三角板如图2所示拼在一起，那么图中∠ADE是度。4、等腰三角形一腰上的中线将这个等腰三角形的周长分成15和6两部分，则这个等腰三角形的三边长是_________________。5、若过m边形的一个顶点有7条对角线，n边形没有对角线，k边形有k条对角线，求(m－k)n的值__________。6、为了使一扇旧木门不变形，木工师傅在木门的背面加钉了一根木条，这样做使用的数学道理是。7、在△ABC中，∠A=3∠B，∠A－∠C=30°，则∠A=____，∠B=____，∠C=______。8、一个三角形周长为27cm，三边长比为2∶3∶4，则最长边比最短边长　　　　。9、一个多边形的内角和与外角和的差是180°则这个多边形的边数为________。10、如果三角形的一个外角等于和它相邻的内角的４倍，等于与它不相邻的一个内角的２倍，则此三角形各内角的度数是　　，　，　。11、一个正多边形的内角和是1440°，则此多边形的边数是_________。 12、已知△ABC的周长是偶数，且a=2，b=7，则此三角形的周长是_________。图1图2二、选择题（每小题3分，共30分）1、下列长度的三条线段可以组成三角形的是（）（A）3、4、2（B）12、5、6（C）1、5、9（D）5、2、72、三角形的两边分别为3和5,则三角形周长y的范围是()A.2＜y＜8B.10＜y＜18C.10＜y＜16D.无法确定3、将一个ABC进行平移，其不变的是（）（A）面积（B）周长（C）角度（D）以上都是4、在平面直角坐标系中，点A（-3，0），B（5，0），C（0，4）所组成的三角形ABC的面积是（）A、32；B、4；C、16；D、85、以长为13cm、10cm、5cm、7cm的四条线段中的三条线段为边，可以画出三角形的个数是（）(A)1个(B)2个(C)3个(D)4个6、给出下列命题：①三条线段组成的图形叫三角形②三角形相邻两边组成的角叫三角形的内角③三角形的角平分线是射线④三角形的高所在的直线交于一点，这一点不在三角形内就在三角形外⑤任何一个三角形都有三条高、三条中线、三条角平分线⑥三角形的三条角平分线交于一点，且这点在三角形内。正确的命题有()A.1个B.2个C.3个D.4个7、...依次观察左边三个图形，并判断照此规律从左向右第四个图形是（）ABDCE图4（A）（B）（C）（D）8、如图4,ABC是等边三角形，点D是BC上一点，，ABD经旋转后至ACE的位置，则至少应旋转（）（A）（B）（C）（D）9、等腰三角形的底边BC=8cm，且|AC－BC|=2cm，则腰长AC为()A.10cm或6cmB.10cmC.6cmD.8cm或6cm10、如果在△ABC中，∠A＝70°－∠B，则∠C等于（）A、35°B、70°C、110°D、140°三、解答题1、在△ABC中，∠A=（∠B＋∠C）、∠B－∠C=20°，求∠A、∠B、∠C的度数。2、如图,在△ABC中,∠ABC与∠ACB的平分线交于点I,根据下列条件求∠BIC的度数.(1)若∠ABC=50°,∠ACB=80°,则∠BIC=______； (2)若∠ABC+∠ACB=116°,则∠BIC=______；(3)若∠A=56°,则∠BIC=_____；(4)若∠BIC=100°,则∠A=______；(5)通过以上计算，探索出您所发现规律：∠A与∠BIC之间的数量关系是_________________________________。ABDCE3、（8分）如图，已知∠DAB+∠D=180°，AC平分∠DAB，且∠CAD=25°，∠B=95°（1）求∠DCA的度数；（2）求∠DCE的度数。PP4、如图，AB∥CD，分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系，请你从所得到的关系中任选一个加以说明。（适当添加辅助线，其实并不难）AABBBAABPPDDCCCCDD（2）（4）（3）（1）第八章二元一次方程组一、知识定义二元一次方程：含有两个未知数，并且未知数的指数都是1，像这样的方程叫做二元一次方程，一般形式是ax+by=c(a≠0,b≠0)。二元一次方程组：把两个二元一次方程合在一起，就组成了一个二元一次方程组。二元一次方程的解：一般地，使二元一次方程两边的值相等的未知数的值叫做二元一次方程组的解。二元一次方程组的解：一般地，二元一次方程组的两个方程的公共解叫做二元一次方程组。消元：将未知数的个数由多化少，逐一解决的想法，叫做消元思想。代入消元法：将一个未知数用含有另一个未知数的式子表示出来，再代入另一个方程，实现消元，进而求得这个二元一次方程组的解，这种方法叫做代入消元法，简称代入法。 加减消元法：当两个方程中同一未知数的系数相反或相等时，将两个方程的两边分别相加或相减，就能消去这个未知数，这种方法叫做加减消元法，简称加减法。二、经典例题例1例2例3如果是同类项，则、的值是（    ）A、＝－3，＝2    B、＝2，＝－3 C、＝－2，＝3    D、＝3，＝－2第八章二元一次方程组复习练习题一、填空题1、关于X的方程，当__________时，是一元一次方程；当___________时，它是二元一次方程。2、已知，用表示的式子是___________；用表示的式子是___________。当时___________；写出它的2组正整数解______________。3、若方程2x+y=是二元一次方程，则mn=。4、已知与有相同的解，则＝__，＝。5、已知，那么的值是。6、如果那么_______。7、若（x—y）2+|5x—7y-2|=0，则x=________，y=__________。8、已知y＝kx＋b，如果x＝4时，y＝15；x＝7时，y＝24，则k＝；b＝．9、已知是方程的一个解,则。10、二元一次方程4x+y=20的正整数解是______________________。11、从1分、2分、5分的硬币中取出5分钱，共同__________种不同的取法（不论顺序）。 12、方程组的解是_____________________。13、如果二元一次方程组的解是，那么a+b=_________。14、方程组的解是15、已知6x－3y=16，并且5x＋3y=6，则4x－3y的值为。16、若是关于、的方程的一个解，且，则＝。17、已知等腰三角形一腰上的中线将它的周长分为63和36两部分，则它的腰长是____。底边长是____。18、已知点A(－y－15，－15－2x)，点B（3x，9y）关于原点对称，则x的值是______，y的值是_________。二、选择题。1、在方程组、、、、、中，是二元一次方程组的有（）A、2个B、3个C、4个D、5个2、二元一次方程组的解是（）A．B．C．D．3、三个二元一次方程2x+5y—6=0，3x—2y—9=0，y=kx—9有公共解的条件是k=（）A．4B．3C．2D．14、如图，8块相同的小长方形地砖拼成一个长方形，其中每一个小长方形的面积为（）A.400cm2B.500cm2C.600cm2D.675cm25、一杯可乐售价1.8元，商家为了促销，顾客每买一杯可乐获一张奖券，每三张奖券可兑换一杯可乐，则每张奖券相当于()(A)0.6元(B)0.5元(C)0.45元(D)0.3元6、已知是方程组的解，则、间的关系是（）A、B、C、D、7、为保护生态环境，陕西省某县响应国家“退耕还林”号召，将某一部分耕地改为林地，改变后，林地面积和耕地面积共有180平方千米，耕地面积是林地面积的25%，为求改变后林地面积和耕地面积各多少平方千米。设改变后耕地面积x平方千米，林地地面积y平方千米，根据题意，列出如下四个方程组，其中正确的是（） ABCD三、解答题。1、在y=中,当时y的值是,时y的值是,时y的值是,求的值,并求时y的值。70cm3m50cm2、有三把楼梯，分别是五步梯、七步梯、九步梯，每攀沿一步阶梯上升的高度是一致的。每把楼梯的扶杆长（即梯长）、顶档宽、底档宽如图所示，并把横档与扶杆榫合处称作联结点（如点A）。2.5m40cm60cm（1）通过计算，补充填写下表：楼梯种类两扶杆总长（米）横档总长（米）30cm2m联结点数（个）五步梯42．050cmA10七步梯九步梯（2）一把楼梯的成本由材料费和加工费组成，假定加工费以每个个联结点1元计算，而材料费中扶杆的单价与横档的单价不相等（材料损耗及其它因素忽略不计）。现已知一把五步梯、七步梯的成本分别是26元、36元，试求出一把九步梯的成本。第八章二元一次方程组复习测试题一、填空题1、如果是一个二元一次方程，那么数．b=______。2、已知方程，写出用表示的式子得___________________。当时,_______。3、已知，则x与y之间的关系式为__________________。4、方程的正整数解是______________。5、已知方程组，不解方程组则x+y=__________。6、已知点A(3x－6，4y＋15)，点B（5y，x）关于x轴对称，则x＋y的值是________。 7、若，则＝，＝。8、已知等腰三角形一腰上的中线将它的周长分为6和9两部分，则它的底边长是_________。9、在△ABC中，∠A－∠C=25°，∠B－∠A=10°，则∠B=________。10、已知二元一次方程组的解为,则。11、已知是方程组的解,则12、有一个两位数，它的两个数字之和为11，把这个两位数的个位数字与十位数字对调，所得的新数比原数大63，设原两位数的个位数字为，十位数字为，则用代数式表示原两位数为，根据题意得方程组。二、选择题1、已知都满足方程y=kx-b，则k、b的值分别为（）A.一5，—7B.—5，—5C.5，3D.5，72、若方程组的解满足＞0，则的取值范围是（）A、＜－1B、＜1C、＞－1D、＞13、下列六个方程组中,是二元一次方程组的有()①②③④⑤⑥A.1个B.2个C.3个D.4个4、如右上图，AB⊥BC，∠ABD的度数比∠DBC的度数的两倍少15°，设∠ABD和∠DBC的度数分别为x、y，那么下面可以求出这两个角的度数的方程组是（）A、B、C、D、5、今年甲的年龄是乙的年龄的3倍，6年后甲的年龄就是乙的年龄的2倍，则甲今年的年龄是（）A、15岁B、16岁C、17岁D、18岁6、当时，代数式的值为6，那么当时的值为（） A、6B、－4C、5D、17、下列各组数中①②③④是方程的解的有()A.1个B.2个C.3个D.4个8、若实数满足（x＋y＋2）(x＋y－1)=0，则x＋y的值为（）A、1B、－2C、2或－1D、－2或1三、解答题（每小题7分，共42分）1、用两种方法求方程组的解①代入法:②加减法:2、已知y=x2＋px＋q，当x=1时，y的值为2；当x=－2时，y的值为2。求x=－3时y的值。3、甲、乙两人共同解方程组,由于甲看错了方程①中的,得到方程组的解为；乙看错了方程②中的,得到方程组的解为。试计算的值.4、如图，宽为50cm的长方形图案由10个相同的小长方形拼成，求每块长方形的长和宽分别是多少？5、一批货物要运往某地，货主准备租用汽车运输公司的甲、乙两种货车，已知过去两次租用这种货车的情况如下表：项目第一次第二次甲种货车辆数/辆25乙种货车辆数/辆36 累计运货吨数/吨15．535现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货，如果按每吨付运费30元计算，问：货车应付运费多少元？6、某纸品加工厂为了制作甲、乙两种无盖的长方体小盒（如图），利用边角料裁出正方形和长方形两种硬纸片，长方形的宽与正方形的边长相等。规格150张正方形硬纸片和300张长方形硬纸片全部用于制作这两种小盒，可以做成甲、乙两种小盒各多少个？第九章不等式与不等式组二、知识定义不等式：一般地，用符号“＜”“＞”“≤”“≥”表示大小关系的式子叫做不等式。不等式的解：使不等式成立的未知数的值，叫做不等式的解。不等式的解集：一个含有未知数的不等式的所有解，组成这个不等式的解集。一元一次不等式：不等式的左、右两边都是整式，只有一个未知数，并且未知数的最高次数是1，像这样的不等式，叫做一元一次不等式。一元一次不等式组：一般地，关于同一未知数的几个一元一次不等式合在一起，就组成了一个一元一次不等式组。一元一次不等式组的解集：一元一次不等式组中各个不等式的解集的公共部分，叫做这个一元一次不等式组的解集。三、定理与性质不等式的性质：不等式的基本性质1：不等式的两边都加上（或减去）同一个数（或式子），不等号的方向不变。不等式的基本性质2：不等式的两边都乘以（或除以）同一个正数，不等号的方向不变。不等式的基本性质3：不等式的两边都乘以（或除以）同一个负数，不等号的方向改变 四、经典例题例1当x时，代数代2-3x的值是正数。例2一元一次不等式组的解集是（    ）A．-2＜x＜3   B．-3b用”>”或”<”连接下列各式；（1）a-3----b-3,(2)2a-----2b,(3)------－(4)4a-3----4b-3(5)a-b---02、不等式3（x-2）＜x-1的非负整数解是3、不等式组的整数解是_______________________4、已知不等式5（x－2）+8<6（x－1）+7的最小整数解是方程2x－ax=4的解，则a的值是____________________。5、如果关于x的不等式(a-1)x