2020小升初重点中学初一新生入学分班摸底数学考试测试卷及答案 5套 39页

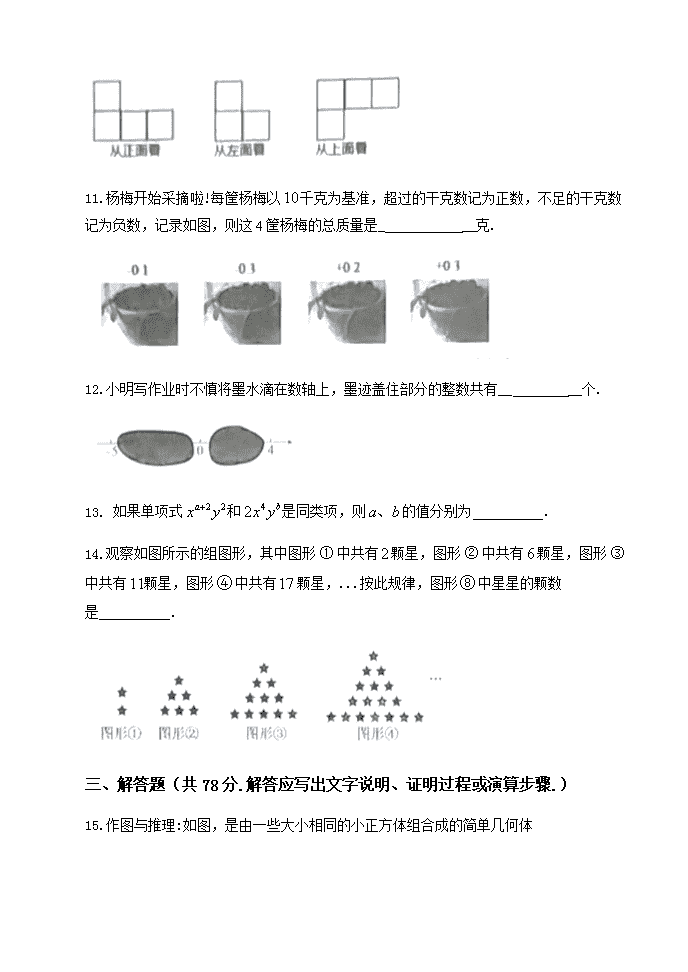
‎2020小升初重点中学新生入学分班摸底数学考试测试卷及答案（一）‎ 一、选择题：本大题共8个小题,每小题3分,共24分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.如图是由儿个大小相同的小正方体搭成的儿何体从上面看到的图形，小正方形中的数字表示该位置上小正方体的个数，则该几何体从左面看到的形状是（ ）‎ A． B． C． D． ‎ ‎2. 用一个平面去截一个几何体，得到的截面是四边形，这个几何体可能是（ ）‎ A．圆锥 B．圆柱 C．球体 D．以上都有可能 ‎ ‎3. 下列说法，其中正确的个数为（ ）‎ 正数和负数统称为有理数:‎ 一个有理数不是整数就是分数:‎ 有最小的负数，没有最大的正数:‎ 符号相反的两个数互为相反数:‎ 一定在原点的左边。‎ A．个 B．个 C．个 D．个 ‎4. 下列运算结果为正数的是（ ）‎ A． B． C. D．‎ ‎5. 目前，中国网民已经达到人，将数据用科学记数法表示为（ ）‎ A． B． C. D．‎ ‎6.如图，把半径为的圆放到数轴上，圆上点与表示的点重合，圆沿着数轴正方向滚动一周，此时点表示的数是（ ）‎ A． B． ‎ C． D．‎ ‎7. 若代数式的值是，则代数式的值是 （ ）‎ A． B． C． D．‎ ‎8. 如果规定符号“”的意义为:，则的值是（ ）‎ A． B． ‎ C． D．‎ 二、填空题（每题3分，满分18分，将答案填在答题纸上）‎ ‎9.一个直角三角形绕其直角边旋转一周得到的几何体是 ．‎ ‎10.一个几何体由若干个大小相同的小正力体搭成，如图是从三个不同方向看到的形状图，则搭成这个几何体所用的小正方体的个数是 ．‎ ‎11.杨梅开始采摘啦!每筐杨梅以千克为基准，超过的干克数记为正数，不足的干克数记为负数，记录如图，则这筐杨梅的总质量是_ __克.‎ ‎12.小明写作业时不慎将墨水滴在数轴上，墨迹盖住部分的整数共有__ __个.‎ ‎13. 如果单项式和是同类项，则的值分别为 ．‎ ‎14.观察如图所示的组图形，其中图形中共有颗星，图形中共有颗星，图形中共有颗星，图形中共有颗星，...按此规律，图形中星星的颗数是 ．‎ 三、解答题（共78分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎15.作图与推理:如图，是由一些大小相同的小正方体组合成的简单几何体 该几何体中有___ 个小正方体；‎ 该几何体从正面看如图所示，请在方格纸中分别画出从左面看和从上面看到的图形.‎ ‎16.一个几何体从三个方向看到的图形如图所示(单位:).‎ 写出这个几何体的名称；‎ 若其从上面看为正方形，根据图中数据计算这个几何体的体积.‎ ‎17.如图，把一张长厘米、宽厘米的长方形纸板分成两个相同的直角三角形.‎ 甲三角形(如图)旋转一周，可以形成一个怎样的几何体?它的体积是多少立方厘米?‎ 三角形(如图③)旋转一周，可以形成一个怎样的几何体?它的体积是多少立方厘米?‎ ‎18. 计算 ‎19.邮递员骑摩托车从邮局出发，先向东骑行到达村，继续向东骑行到达村，然后向西骑行到村，最后回到邮局.‎ 以邮局为原点，以向东方向为正方向，用个单位长度表示，请你在数轴上表示出三个村庄的位置；‎ 村离村有多远?‎ 若摩托车每耗油升，这趟路共耗油多少升?‎ ‎20.已知互为相反数，互为倒数，的绝对值为,试求的值.‎ ‎21. 在某地，人们发现在一定温度下某种蟋蟀叫的次数与温度之间有如下的近似关系，用蟋蟀叫的次数除以.然后再加上.就近似地得到该地当时的温度 用代数式表示该地当时的温度；‎ 当蟋蟀叫的次数分别是和时，该地当时的温度的是多少?‎ ‎22. 先化简，再求值:，其中.‎ ‎23.如图是小明家的住房结构平面图(单位:米)，他打算把卧室以外的部分都铺上地砖.‎ 若铺地砖的价格为元平方米，那么购买地砖需要花多少钱(用代数式表示)?‎ 已知房屋的高为米，现需要在客厅和卧室的墙壁上贴壁纸，那么需要多少平方米的壁纸(计算时不扣除门、窗所占的面积)（用代数式表示)?‎ ‎24.问题:你能比较两个数与 的大小吗?为了解决这个问题，我们先把它抽象成这样的问题:写成它的一般形式，即比较和的大小(是非零自然数).然后，我们分析...这些简单情形入手，从而发现规律，经过归纳，猜想出结论.‎ 通过计算，比较下列各组中两个数的大小 ‎_ __；_ __；_ __‎ ‎____ __；_ __；_ __‎ 从第题的结果经过归纳，可以猜想和的大小关系；‎ 根据上面归纳猜想得到的-般结论， 试比较下列两个数的大小:‎ ‎ ‎ 参考答案 一、 选择题（每小题3分，共24分）‎ ‎ 1、D 2、B 3、A 4、C 5、B 6、C 7、D 8、A ‎ 二、 填空题（每小题3分，共18分）‎ ‎9.圆锥 10.5 11.40.1 12.7 13.2,2 14.51‎ 三、计算题（共78分）‎ ‎15.解：（1）2×5+1=11（块）．故图1中有11块小正方体； ‎ ‎（2）如图所示：‎ ‎16.解：(1)长方体 (2)由题可知，长方体的底面是边长为3cm的正方形，高是4cm，‎ 则这个几何体的体积是3×3×4=36(cm3).‎ 答：这个几何体的体积是36cm3. ‎ 17. 解：(1)甲三角形旋转一周可以形成一个圆锥体， ‎ 它的体积是×3.14×62×10=376.8(立方厘米).‎ (2) 乙三角形旋转一周可以形成一个空心的圆柱， ‎ 它的体积是3.14×62×10－×3.14×62×10=753.6(立方厘米). ‎ ‎18.（1）（-17）+21 =-4 ‎ ‎ （2）（-21.6）+3-7.4+(-) ‎ ‎ =-21.6-7.4-+3 ‎ ‎ =-26 ‎ （3） ‎-0.1÷×(-100) ‎ ‎ =×2×100 ‎ ‎=20‎ ‎（4）23÷[(-2)3-(-4)]‎ ‎ =23÷[(-8)-(-4)] ‎ ‎=23÷(-4)‎ ‎ =- ‎ ‎19.解：(1)依题意，得数轴为 ‎ (2)依数轴，得点C与点A的距离为2＋4=6 (km)． ‎ ‎(3)依题意，得邮递员骑了2＋3＋9＋4=18 (km)，‎ 共耗油量18×0.03=0.54(升)．‎ 答：这趟路共耗油0.54升． ‎ ‎20.解：因为a，b互为相反数，c，d互为倒数，e的绝对值为3，‎ 所以a＋b=0，cd=1，e=±3.‎ 所以原式＝0÷108－(±3)2÷[(－1)2019－2]‎ ‎＝(－9)÷(－1－2)＝(－9)÷(－3)＝3. ‎ 21. 解：（1）设蟋蟀1min叫的次数用x表示，‎ 则该地当时的温度可以表示为：(+3)0C ‎ ‎ (2)当蟋蟀1min叫的次数是84时：+3=+3=12+3=150C ‎ ‎ 当蟋蟀1min叫的次数是105时：+3=+3=15+3=180C ‎ 当蟋蟀1min叫的次数是126时：+3=+3=18+3=210C ‎ ‎22.解：原式=6a2－6ab－12b2－6a2＋12b2=－6ab.‎ 当a=－，b=－8时，‎ 原式=－6×（）×(－8)=－24. ‎ ‎23.解：(1)铺地砖的面积为2x·4y＋x·2y＋xy＝11xy(平方米).‎ 则购买地砖需要花80×11xy＝880xy(元).‎ ‎ [2(2x＋4y)＋2(2x＋2y)]×3＝(24x＋36y)(平方米).‎ 即需要(24x＋36y)平方米的壁纸. ‎ ‎24.解：（1）①∵12=1，21=2， ∴12＜21； ②∵23=8，32=9， ∴23＜32； ③∵34=81，43=64， ∴34＞43； ④∵45=1024，54=625， ∴45＞54； ⑤∵56=15625，65=7776， ∴56＞65； ⑥∵67=279936，76=117649， ∴67＞76； （2）n＜3时，nn+1＜（n+1）n， n≥3时，nn+1＞（n+1）n； （3）∵2018＞3， ∴20182019＞ 20192018． ‎ ‎2020小升初重点中学新生入学分班摸底数学考试测试卷及答案（二）‎ ‎（本试卷满分为 100 分，考试时间为 60 分钟）‎ 一、认真读题，谨慎填空 （每小题 2 分，共 20 分）‎ ‎1、宏伟的上海世博场馆框架共用了焊接口149500000 个，改成用“万”作单位的数 是(‎ ‎)万个，用“亿”作单位并保留两位小数约是(‎ ‎)亿个.‎ ‎2、小明上楼梯，他从一楼上到四楼需要30 秒，那么他从四楼上到九楼，需要（ ）‎ 秒.‎ ‎3、3.25 小时=（‎ ‎）分； 7 公顷8 平方米=（‎ ‎）小时（‎ ‎）平方米.‎ ‎6‎ ‎13‎ ‎） % .‎ ‎4、 ( ) = 52 =（‎ ‎5、把一根5 米的绳子平均分成8 段，最后一段长（‎ ‎）、两段占全长的（‎ ‎）.‎ ‎1‎ ‎3‎ ‎6、把33.3% 、 、 、p 、0.332 按从小到大排列起来:‎ ‎3 10‎ ‎ .‎ ‎7、 x ¸ y = 1.8, x + y = 28 ( x 、 y 为自然数)，那么 x =（‎ ‎）， y =（‎ ‎）.‎ ‎8、小张打一份稿件从5 小时缩短了2 小时后，工作效率提高了（‎ ‎（精确到0.1% ）‎ ‎） % .‎ ‎9、一个三角形的三个内角度数的比是 3∶2∶1，这个三角形中最大的一个内角是 ‎(‎ ‎)度，它是一个(‎ ‎)三角形.‎ ‎10、一个圆柱的底面半径和高相等，它的表面积是50.24 平方厘米，这个圆柱的体积 是（‎ ‎）立方厘米.‎ 二、仔细推敲，认真辨析(每小题 2 分，共 10 分)‎ ‎1、在 6.8 的末尾添上一个零后，计数单位是（‎ ‎） 十分位 ‎)统计图.‎ 折线 ‎① 0.1‎ ‎② 0.01‎ ‎③‎ ‎④ 百分位 ‎2、反映儿童牛奶中各种营养成份的含量选用(‎ ‎① 扇形 ‎② 条形 ‎③‎ http://www.1ydt.cn/‎ ‎3、在含糖率为10% 的糖水中，加入2 克糖和8 克水，这时糖水的含糖率（‎ ‎）‎ ‎① 大于10%‎ ‎②小于10%‎ ‎③等于10%‎ ‎3‎ ‎3‎ ‎4、甲÷ 5 =乙× (1 - 8) ，那么甲比乙（‎ ‎）‎ ‎① 大 ‎② 小 ‎③ 相等 ‎5、在比例尺10 ∶1 中，实际距离是8 毫米的物体，它的图上距离是（‎ ‎）.‎ ‎① 8 厘米 ‎② 8 分米 ‎③ 8 毫米 三、认真思考，慎重判断.（对的打“√”，错的打“×”，本题 5 分）‎ ‎1、永不相交的两条直线叫做平行线.----------------------------------（‎ ‎2、若3a - b = 0（ a 不等于 0），则a 和b 成正比例.----------------------（‎ ‎3、两个完全一样的正方体合并成一个长方体后的表面积是原来总表面积 ‎5‎ 的 6 .---------------------------------------------------------（‎ ‎4、一种商品先降价20% ，后又提价25% ，所以又回到了原价.-------------（‎ ‎）‎ ‎）‎ ‎）‎ ‎）‎ ‎1‎ ‎1‎ ‎5、冰化成水体积减少 ，那么水结成冰体积增加 .---------------------（‎ ‎）‎ ‎10‎ 四、一丝不苟，巧妙计算（共 29 分）‎ ‎11‎ ‎1、直接写出得数.（每小题 1 分，共 8 分）‎ ‎1 + 1 =‎ ‎374 -198 = ‎4 ¸ 0.22 =‎ ‎9.03+7%=‎ ‎3 4‎ ‎(估算)‎ ‎2 ¸ 3 + 1 = ‎53.92 ¸ 5.9 » ‎7 -1.3 - 2.7 = ‎6‎ ‎2 ´ 0.3 ¸ 2 ´ 0.3 = ‎2、用递等式计算（能简算的要简算）.（每小题 3 分，共 15 分）‎ ‎12 ´（1 + 3 - 1)‎ ‎10 ¸ 5 + 5 ´ 4‎ ‎303×99＋303‎ ‎6 4 2‎ ‎9 9‎ ‎100 - 40 ¸17 ´ 17‎ ‎13 - æ 4 - 3 ö + 4‎ ç 5 8 ÷ ‎25‎ ‎8‎ è ø ‎5‎ ‎3、求未知数 x .（每小题 3 分，共 6 分）‎ ‎5 : 3‎ ‎7.2 ´ 3 - 7x = 0.6‎ = 8 : x ‎4 4‎ ‎8‎ 五、图形操作，解决问题.（共 5 分） 1、作三角形 AB 边上的高.（2 分）‎ ‎2、右图长方形的面积是18 平方厘米,‎ 求圆的面积.（3 分）‎ 六、活用知识，解决问题.（共 32 分）‎ ‎1、只列式不计算（每小题 2 分，共 8 分）‎ ‎（1）一种优质大米的出米率为78% ，要碾出117 千克大米，需要谷子多少千克？‎ ‎（2）学校刚竣工的学生宿舍楼投资了70 万元，比计划节约了10 万元，节约了百分之 几？ ‎ ‎1‎ ‎（3）小明3 天看了这本的 4 ，照这们计算，还要多少天才能看完？‎ ‎（4）小王在今年的二月下旬加工一批零件，前3 天共加工零件210 个，在剩下的几天 里平均每天加工55 个，这个下旬平均每天加工零件多少个？‎ ‎2、专业组平整工地，原计划每天平整0.4 公顷，15 天可以完成任务；实际提前4 天 完成任务，实际每天平整多少公顷？（4 分）‎ ‎3、去年年底我国南方遭受特大雪灾,姐弟俩积极捐款支援灾区,弟弟捐了40 元,比姐 姐捐的 少5 元,姐弟俩共捐了多少元?（4 分）‎ ‎8‎ ‎5‎ ‎4、在一个底面半径为8 厘米，高为12 厘米的圆柱体容器中装满水，现将两个底面半径都为3 厘米，高为6 厘米的圆锥完全放入水中，把它们取出后容器的水低了多少厘 米？（5 分）‎ ‎1‎ ‎5、甲、乙两队共有职工100 人，如果抽调甲队的 4 到乙队，乙队人数就比甲队人数 ‎2‎ 多 ，甲队原有多少人？（5 分）‎ ‎9‎ ‎6、甲、乙两车分别从 A 、B 两地出发相向而行，相遇前，甲、乙两车的速度比是5 ∶ 4 ，‎ 相遇后，甲车的速度减少20% ，乙车的速度不变，这样甲车到达离 B 地还差全长的 9‎ 时，乙车离 A 地还有40 千米，那么 A 、 B 两地相距多少千米？（6 分）‎ ‎1‎ 答案 一．1、14950，‎ ‎1.50‎ ‎2、50‎ ‎5、0.625 米， 1‎ ‎4‎ ‎8、66.7%‎ ‎3、‎ ‎3，15，70008‎ ‎3‎ < 0.332 < 33.3% < 1 < p ‎4、24，25‎ ‎6、‎ ‎10‎ ‎3‎ ‎7、18，10‎ ‎10、25.12‎ 二．②①①②① 三．×√√√×‎ ‎9、90，直角 ‎7‎ ‎12‎ ‎5‎ 四．1、176，‎ ‎，9.1，100，9，3， ，0.09‎ ‎6‎ ‎2‎ ‎2、30300，5， 20 ，98.4，2‎ ‎9‎ ‎3、 x = 4.8 ， x = 0.3‎ 五．1、作图略 ‎2、28.26 平方厘米 ‎（2）10 ¸ (70 +10)´100%‎ ‎（4） éë210 + 55(8 - 3)ùû ¸ 8‎ 六．1、（1）117 ¸ 78%‎ ‎1‎ ‎（3） 3 ¸ - 3‎ ‎4‎ ‎6‎ ‎11‎ ‎2、‎ ‎3、112‎ ‎4、2 ´ 1 ´ 3.14 ´ 32 ´ 6 = 113.04 ，113.04 ¸ (3.14 ´ 82 )= 0.5625 （厘米）‎ ‎3‎ ‎5、100 ¸ æ1 + 1 + 2 ö ¸ æ1 - 1 ö = 60 （人）‎ ç ‎9 ÷ ç 4 ÷ è ø è ø ‎6、因为相遇前，甲、乙两车的速度比是5 ∶ 4 ；‎ ‎5‎ ‎4‎ ‎4‎ ‎5‎ 所以相遇时，甲走了全程的 ，还剩 ，乙走了全程的 ，还剩 ；‎ ‎9‎ ‎9‎ ‎9‎ ‎9‎ ‎4‎ ‎1‎ ‎3‎ 相遇后甲走了全程的 - = ‎9 9 9‎ 因为相遇后两人的速度相同，‎ ‎3‎ ‎5‎ ‎3‎ ‎2‎ 所以相遇后乙也走了全程的 ，还剩下 - = ，‎ ‎9‎ ‎9 9 9‎ ‎2‎ 所以全程为40 ¸ = 180 （千米）‎ ‎9‎ ‎2020小升初重点中学新生入学分班摸底数学考试测试卷及答案（三）‎ 一、填空题：‎ ‎　　 　　2．123×5.67+8.77×567=______.‎ ‎　　3．如图，有三个同心半圆，它们的直径分别为2，6，10，用线段分割成9块，如果每块字母代表这一块的面积并且相同的字母代表相同的面积，那么（A+B）：C=______.‎ ‎　　 等于______.‎ ‎　　5．小刚，小强两人骑车的速度之比是15∶13，如果小刚，小强分别由甲、乙两地同时出发，相向而行，半小时后相遇；如果他们同向而行，那么小刚追上小强需要_______小时．‎ ‎　　6．5个正方体的六个面上分别写着1、2、3、4、5、6六个数，并且它们任意两个相对的面上所写的两个数的和都等于7．现在把五个这样的正方体一个挨着一个地连接起来（如图），在紧挨着的两个面上的两个数之和都等于8，那么，图中打“？”的这个面上所写的数是______.‎ ‎　　7．先任意指定7个整数，然后将它们按任意顺序填入2×7方格表第一行的七个方格中，再将它们按任意顺序填入方格表第二行的方格中，最后，将所有同一列的两个数之和相乘．那么，积是______数（填奇或偶）．‎ ‎　　8．有两组数，第一组数的平均数是13．6，第二组数的平均数是10.8，而这两组数总的平均数是12.4，那么，第一组数的个数与第二组数的个数的比值是______.‎ ‎　　9．有四个数，每次选取其中三个数，算出它们的平均数，再加上另外一个数，用这种方法计算了四次，分别得到以下四个数：72，98，136，142，那么，原来四个数的平均数是______.‎ ‎　　10．体育组有一筐球，其中足球占45％，如果再放入5个篮球，足球就只占36％，那么，这筐球中，足球有______个．‎ 二、解答题：‎ ‎　　1．松鼠妈妈采松籽，晴天每天可以采20个，有雨的天每天只能采12个．它一连几天采了112个松籽，平均每天采14个．那么，这几天中有几天有雨？‎ ‎　　2．有6块岩石标本，它们的重量分别是8.5千克、6千克、4千克、4千克、3千克、2千克，要把它们分别装在3个背包里，要求最重的一个背包尽可能轻一些．请写出最重的背包里装的岩石标本是多少千克？‎ ‎　　3．上午8时8分，小明骑自行车从家里出发，8分后，爸爸骑摩托车去追他，在离家4千米的地方追上了他，然后爸爸立刻回家．到家后又立刻回头去追小明，再追上他的时候，离家恰好是8千米，问这时是几时几分？‎ ‎　　4．70个数排成一行，除了两头的两个数以外，每个数的三倍都恰好等于它两边两个数的和，这一行最左边的几个数是这样的：0，l，3，8，21，…．问最右边一个数被6除余几？‎ 参考答案 一、填空题：‎ ‎　　 　　‎ ‎　　2．5670‎ ‎　　‎ ‎　　3．55∶48‎ ‎　‎ ‎　　 　　 　　 ‎ ‎　　 　　 　　‎ ‎　　5．7‎ ‎　　设小刚的速度是15份，小强的速度是13份．相向而行，甲、乙距离＝(15＋13)×0.5同向而行，甲、乙距离＝(15—13)×追及时间，所以，(15 即：小刚追上小强需要7小时．‎ ‎　　6．4‎ ‎　　前面2的对面是5，5紧挨着3，3的对面是4，4紧挨着4，4的对面是3，上面的2的对面是5，所以，拐弯那块正方体已知四面数字：上面是2，下面是5，前面是4，后面是3，因此，左、右两面只能是1、6‎ ‎，假设右面是1，1紧挨着7才能使和是8，但六个数字：1至6中没有7，所以右面不能是1，故，右面只能是6，6紧挨着2，2的对面是5，5紧挨着3，3的对面是4，所以打“？”的这个面所写的数字是4．‎ ‎　　7．偶 ‎　　7个整数中，奇、偶数的个数必不相等，因此，每一列的两个数不可能奇、偶性都不同，即：至少有一列的两数之和是偶数．‎ ‎　　‎ ‎　　第一组数平均每个数比总平均数多 ‎　　13.6-12.4＝1.2‎ ‎　　总共多1.2×第一组数的个数；‎ ‎　　第二组数平均每个数比总平均数少 ‎　　12.4-10.8＝1.6‎ ‎　　总共少了1.6×第二组数的个数；‎ ‎　　一多一少，两者抵消，因此，‎ ‎　　1.2×第一组的个数＝1.6×第二组的个数即：‎ ‎　　‎ ‎　　9．56‎ ‎　　 了它本身，即四次计算中，每个数相当于被取到过两次，因此，上面四个数的和就是原来四个数的和的2倍，那么，原来四个数的平均数是：‎ ‎　　(72＋98＋136＋142)÷2÷4＝56．‎ ‎　　10．9‎ ‎　　原来足球与其它球的比是：‎ ‎　　45%∶(1-45%)＝9∶11‎ ‎　　设足球有9份，其它球有11份，现在足球与其它球之比是：‎ ‎　　36%∶(1-36%)＝9∶16‎ ‎　　也就是：11＋5＝16(份)，即：五个篮球＝5份，所以1份＝1个球，于是，有足球9个．‎ ‎　　二、解答题：‎ ‎　　1．6天 ‎　　[20×(112÷14)-112] ÷(20-12)‎ ‎　　＝(160-112)÷8‎ ‎　　＝6(雨天数)‎ ‎　　112÷14-6＝2(晴天数)．‎ ‎　　2．10千克 ‎　　因为三个包的平均重量是9千克多一点，所以，最轻的包只能装8.5千克那一块，其余分为两包，要使最重的包尽量的轻，当然只能是6＋4＝10(千克)．‎ ‎　　3．8时32分 ‎　　爸爸第一次追上小明时，小明走了4千米，爸爸也走了4千米，但小明多用了8分，从第一次追上到第二次追上时，小明走了第2个4千米，爸爸走了12千米．这说明，相同的时间里爸爸可以走12千米，也可以走4千米休息8分，也就是说爸爸在8分里能走12—4＝8‎ 千米，爸爸的速度是每分钟8÷8＝1(千米)，实际上爸爸共走了4＋12＝16(千米)，要用16分的时间，所以第2次追上时是8时32分．‎ ‎　　4．被6除余4‎ ‎　　用2去除最左边的几个数，余数分别是：0，1，1，0，1，…，每三个数一循环，用3去除最左边的几个数余数分别是0，1，0，2，0…，每四个数一循环．因为70÷3，余数是1，说明第70个数是偶数；70÷4余2，说明第70个数被3除余1，因为被3除余1的偶数被6除余4，所以。。。。‎ ‎2020小升初重点中学新生入学分班摸底数学考试测试卷及答案（四）‎ 一、填空题：‎ ‎　　 　　‎ ‎　　3.在下列（1）、（2）、（3）、（4）四个图形中，可以用若干块 ‎　　4．在200至300之间，有三个连续的自然数，其中，最小的能被3整除，中间的能被7整除，最大的能被13整除，那么这样的三个连续自然数是______．‎ ‎ 当它们之中有一个开始喝水时．另一个跳了______米．‎ ‎　　减去的数是______．‎ ‎7．100！=1×2×3×…×99×100，这个乘积的结尾共有______个0．‎ ‎8．一批工人到甲、乙两个工地进行清理工作，甲工地的工作量是乙工 完，乙工地的工作还需4名工人再做1天，那么这批工人有______人．‎ ‎9．如果两数的和是64，两数的积可以整除4875，那么这两个数的差等于______.‎ ‎　　10．甲、乙、丙三人进行100米赛跑，当甲到达终点时，乙离终点还有8米，丙离终点还有12米．如果甲、乙、丙赛跑时速度不变，那么，当乙到达终点时，丙离终点还有______米．‎ 二、解答题：‎ ‎　　1．有一个四位整数，在它的某位数字前面加上一个小数点，再和这个四位数相加，得数是2016.97，求这个四位整数．‎ ‎2．一串数排成一行，它们的规律是这样的：头两个数都是1，从第三个数开始，每一个数都是前两个数的和，也就是：l，1，2，3，5，8，13，21，34，55，…，问：这串数的前100个数中（包括第100个数）有多少个偶数？‎ ‎3．在一根木棍上，有三种刻度线．第一种刻度线将木棍分成10等份；第二种刻度线将木棍分成12等份；第三种刻度线将木棍分成15等份．如果沿每条刻度线将木棍锯断，木棍总共被锯成多少段？‎ ‎4．有甲、乙两个同样的杯子，甲杯中有半杯清水，乙杯中盛满了含50％酒精的溶液，先将乙杯中酒精溶液的一半倒入甲杯，搅匀后，再将甲杯中酒精溶液的一半倒入乙杯．问这时乙杯中的酒精是溶液的几分之几？‎ 参考答案 ‎　　一、填空题：‎ ‎　　1．1601．‎ ‎　　因为819＝7×9×13，所以，‎ ‎　　‎ ‎　　2．1．‎ ‎　　‎ ‎　　3．（2）．‎ ‎　　(1)号图形中有11个小方格，11不是3的整数倍，因此，不能用这两种图形拼成．‎ ‎　　(3)号图形中有15个小方格，15是3的整数倍，但是，左上角和右下角 ‎　　只能用来拼，剩下的图形如图1，显然它不能用这两种图形来拼，只有（2）、(4)号图形可以用这两种图形来拼，具体拼法如图2(有多种拼法，仅举一种)．‎ ‎　　4．258，259，260．‎ ‎　　先找出两个连续自然数，第一个被3整除，第2个被7整除．例如，找出6和7，下一个连续自然数是8．‎ ‎　　3和7的最小公倍数是21，考虑8加21的整数倍，使加得的数能被13整除．‎ ‎　　8＋21×12＝260‎ ‎　　能被13整除，那么258，259，260这三个连续自然数，依次分别能被3，7，13整除，又恰好在200至300之间．‎ ‎　　‎ ‎　　‎ ‎　　6．37．‎ ‎　　画张示意图：‎ ‎　‎ ‎　　(85-减数)是2份，(157-减数)是5份，‎ ‎　　(157-减数)-(85-减数)＝72，它恰好是5-2＝3(份)，因此， 72÷3＝24是每份所表示的数字，减数＝85—24×2＝37．‎ ‎　　7．24．‎ ‎　　结尾0的个数等于2的因子个数和5的因子个数中较小的那个．100！中2的因子个数显然多于5的因子个数，所以结尾0的个数等于100！中的5的因子个数．‎ ‎8．　　‎ ‎　　9．14．‎ ‎　　两数的积可以整除4875，说明这两个数都是4875的约数，我们先把4875分解质因数：‎ ‎　　4875＝3×5×5×5×13‎ ‎　　用这些因子凑成两个数，使它们的和是64，这两个数只能是3×13＝39和5×5＝25．所以它们的差是：39—25＝14．‎ ‎　10.　甲跑100米，乙跑92米，丙跑88米所用时间相同，那么，乙的速度∶‎ ‎　　二、解答题：‎ ‎　　1．1997．‎ ‎　　因为小数点后是97，所以原四位数的最后两位是97；又因为97＋19＝116，所以小数点前面的两位整数是19，这样才能保证19.97＋1997＝2016.97．于是这个四位整数是1997．‎ ‎　　2．33个．‎ ‎　　因为奇数＋奇数是偶数，奇数＋偶数是奇数，偶数＋奇数是奇数，两个奇数相加又是偶数．这样从左到右第3，6，9……个数都是偶数．所以偶数的个数有99÷3＝33(个)．‎ ‎　　3．28段．‎ ‎　　因为，10等分木棍，中间有9个刻度，12等 ‎　　分木棍中间有11个刻度，15等分木棍中间有14个刻度，若这些刻度都不重合，中间应有34个刻度，可把木棍锯成35段．但是，需要把重合的刻 ‎ ‎　‎ ‎　　‎ ‎2020小升初重点中学新生入学分班摸底数学考试测试卷及答案（五）‎ 一、填一填（每小题2分，共20分）‎ ‎1.填上合适的单位名称：一间教室面积是54（   ）  青青体重40（   ）。‎ ‎2.  0.78平方千米=（   ）公顷 ‎4.2吨=（   ）千克。  ‎ ‎3．一个圆锥的底面半径是3厘米，体积为18.84立方厘米，这个圆锥的高是(  )厘米。‎ ‎4.今年的小麦产量比去年的增产二成三,表示今年比去年增产(  )%,也就是今年的产量相当于去年的(  )%。‎ ‎5.一种大豆的出油率是10%，300千克大豆可出油（    ）千克，要榨300千克豆油需大豆（    ）千克。‎ ‎6.一辆公共汽车共载客42人，其中一部分人在中途下车，每张票价6元，另一部分人到终点下车，每张票价9元，售票员共收票款318元，中途下车的有（    ）人。‎ ‎7．一个三位小数“四舍五入”保留两位小数是6.80，这个小数最小可能是（    ），最大可能是（    ）。‎ ‎8.50以内6的倍数有（    ）。  ‎ ‎9.一段木头砍成4段要6分钟，砍成8段要（    ）分钟。‎ ‎10.下面的图形中圆的半径为2㎝，阴影部分的面积为（   ）。‎ 二、选择（每题2分，共12分）‎ ‎1.一件商品，先提价20%，以后又降价20%，现在的价格与原来相比，（）‎ A．提高了B．降低了 C．不变D．无法确定 ‎2.1元和2角的纸币共20张,共15.2元,2角的纸币有(  )张。‎ A.14     B.6     ‎ C.12     D.18‎ ‎3．在钟面上，12时15分的时候，时针和分针所成的角是（     ）‎ A.平角   B.直角   ‎ C.钝角   D.锐角、‎ ‎4．下列图形中，对称轴最多的是（    )。‎ A.长方形        B.正方形      ‎ C.等腰三角形      D.圆 ‎5．两个数的比值是1.2，如果比的前项扩大2倍，后项缩小两倍，比值是（  ）‎ A．1.2   B．2.4   ‎ C．4.8 D．9.6‎ ‎6．王师傅加工一批零件，1/2小时加工了这批零件的3/8，全部加工完还需要（  ）小时。‎ 三、判断（6分）‎ ‎1.在一个比例里，如果内项的积等于1，那么两个外项的积一定是1。（   ）    ‎ ‎2.一个圆和一个正方形的周长相等，比较它们的面积，结果是圆的面积大。（   ）  ‎ ‎3.长方体的底面积一定，高和体积成反比例。（   ）‎ ‎4.小刚在教室中的座位用数对表示为（3，5），代表着他坐在第三行第五列。（   ）  ‎ ‎5.两条线段互相平行，它们也一定相等。（   ）     ‎ ‎6.盒子里有同样大小的红、黄、蓝三种颜色的球各5个，要想摸出的球一定有2个是同色的，至少要摸出4个球。（   ）‎ 四、算一算。（共26分）   ‎ ‎1.能简算的要简算。（12分）‎ ‎2.求未知数的值。（9分）‎ ‎3．图中的两个正方形的边长分别是10厘米和6厘米，求阴影部分的面积．‎ 五、应用题。（每小题5分，共30分）‎ ‎1.一个等腰三角形，底角和顶角的度数比是1：3。它的一个底角是多少度？        ‎ ‎2.新区器材厂用一根长120厘米的铁丝做成一个长方体框架，这个长方体长宽高的比是3：2：1，这个长方体的体积是多少立方厘米？     ‎ ‎3.公园里栽了149棵杨树，再栽上22棵就是所栽柳树的3倍。栽了多少棵柳树？（用方程解答）        ‎ ‎4.食堂买来茄子和土豆共380kg，茄子的质量比土豆的3倍还多8kg，茄子和土豆各有多少千克？‎ ‎5.儿童节期间，学校准备用800元钱买节日礼物，其中30%的钱买糖果，剩余的钱按3：5用来购买文具和图书。学校购买文具和图书各用了多少元?         ‎ ‎6.一个圆柱形的游泳池，底面直径是10米，高是4米。在它的四周和底部涂水泥，每千克水泥可涂5平方米，共需多少千克水泥？‎ 六、图图变换（6分）‎ 画出三角形AOB绕点0点逆时针旋转90°后的图形。‎ 参考答案