北师大版七年级上册-第05讲-一元一次方程（培优）-教案 17页

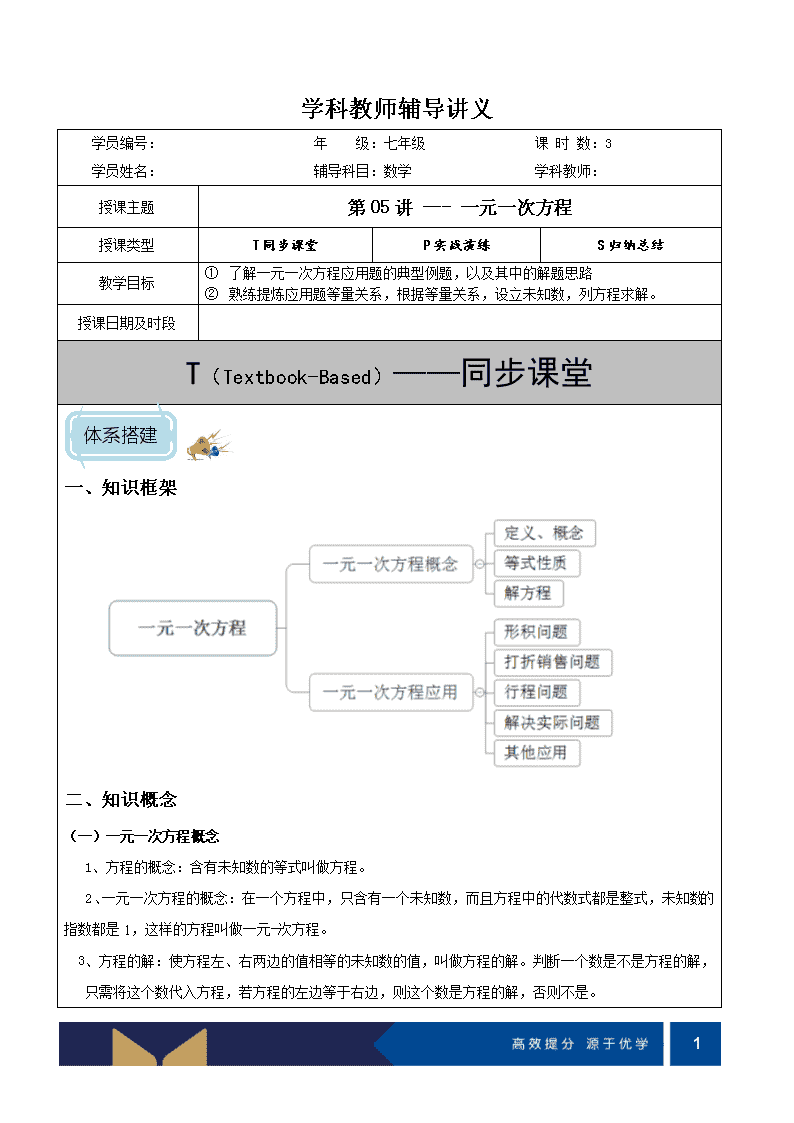
1 学科教师辅导讲义 学员编号： 年 级：七年级 课 时 数：3 学员姓名： 辅导科目：数学 学科教师： 授课主题 第 05 讲 --- 一元一次方程 授课类型 T 同步课堂 P 实战演练 S 归纳总结 教学目标 1 了解一元一次方程应用题的典型例题，以及其中的解题思路 2 熟练提炼应用题等量关系，根据等量关系，设立未知数，列方程求解。 授课日期及时段 T（Textbook-Based）——同步课堂 体系搭建 一、知识框架 二、知识概念 （一）一元一次方程概念 1、方程的概念：含有未知数的等式叫做方程。 2、一元一次方程的概念：在一个方程中，只含有一个未知数，而且方程中的代数式都是整式，未知数 的指数都是 1，这样的方程叫做一元一次方程。 3、方程的解：使方程左、右两边的值相等的未知数的值，叫做方程的解。判断一个数是不是方程的解， 只需将这个数代入方程，若方程的左边等于右边，则这个数是方程的解，否则不是。 2 4、等式基本性质 1：等式两边同时加（或减）同一个代数式，所得结果仍是等式 等式的基本性质 2：等式两边同时乘同一个数（或除以同一个不为 0 的数），所得结果仍是等式。 （二）解一元一次方程 1、移项：方程中的任何一项，都可以在改变符号后，从方程的一边移到另一边，这种变形叫移项。 （三）一元一次方程应用 1、形积问题 2、打折销售问题 1、与打折销售有关的公式： ①利润=售价-成本（进价） ②利润率=利润÷成本价×100% ③售价=成本价+利润=成本价×（1+利润率） ④售价=标价×打折数 3、行程问题 1、相遇问题，它的特点是相向而行，这类问题一般画出示意图帮助分析题意。这类问题的等量关系一般 是：双方所走路程之和=全部路程，这只是常见的等量关系，解题时还需结合实际分析等量关系。 2、追及问题，它的特点是同向而行，等量关系一般是：双方路程之差=原来双方相距的路程。这只是常 见的等量关系，解题时还需结合实际分析等量关系。 3、航行问题：顺水速度=船在静水中的速度+水流速度 逆水速度=船在的静水中速度-水流速度 变形名称 具体做法 变形依据 注意的问题 去分母 在方程两边同时乘各分母的最小 公倍数 等式基本性质 2 不要漏乘不含分母的项， 分数线起到括号的作用 去括号 先去小括号，再去中括号，最后 去大括号 去括号法则、分配律 括号前是负号，去括号后， 括号内各项均变号 移项 把含未知数的项移到方程的一 边，其他项都移到方程的另一边 等式基本性质 1 移项要变号 合并同类项 把方程化为 ( 0)ax b a  的形式 合并同类项法则 系数相加，字母及其指数 均不变 未知数的系 数化为 1 在方程两边同除以未知数的系数 a ，得到方程的解 bx a  等式的基本性质 2 分子、分母不要颠倒 3 4、解决实际问题一般步骤 5、其他应用：工程问题、分配问题等 典例分析 考点一：一元一次方程相关概念 例 1、例 1、若（m-2） 2 3mx  ﹣2m=1，是关于 x 的一元一次方程，则 m=（ ） A．±2 B．2 C．﹣2 D．1 【解析】解：由题意得， 2m ﹣3=1，m-2≠0， 解得，m= -2 故选：C 例 2、已知： 1( 2)2 3( 2 ) 5 0 a a b y y      是关于 y 的一元一次方程： （1）求 a，b 的值 （2）若 x=a 是 ﹣ +3= 的解，求丨 5a﹣2b 丨﹣丨 4b﹣2m|的值 【解析】解：（1）∵ 1( 2)2 3( 2 ) 5 0 a a b y y      是关于 y 的一元一次方程， ∴ a+2b=0， 1 3 a+2=1， ∴ a=﹣3，b= 3 2 （2）把 x=a=﹣3，代入 ﹣ +3= ，m=26， 故原式=﹣28 例 3、 20 9 3x x x  是一元一次方程m +m 的解，则m= 4 【解析】将 x=0 带入方程得 2 9m  ， 3m   ，注意到是一元一次方程， 3 0, 3m m   故 考点二： 解一元一次方程 例 1、我们规定，若关于 x 的一元一次方程 ax=b 的解为 b﹣a，则称该方程为“差解方程”，例如：2x=4 的解 为 2，且 2=4﹣2，则该方程 2x=4 是差解方程． 请根据上边规定解答下列问题： （1）判断 3x=4.5 是否是差解方程；（2）若关于 x 的一元一次方程 6x=m+2 是差解方程，求 m 的值． 【解析】（1）根据差解方程的意义得出 ax=b 的解为 b﹣a，即 b﹣a= b a 解：（1）∵3x=4.5 ∴x=1.5 ∵4.5﹣3=1.5 ∴3x=4.5 是差解方程 （2）∵关于 x 的一元一次方程 6x=m+2 是差解方程， ∴m+2﹣6= ， 解得：m= 例 2、已知关于 x 的方程 ax+2=2（a+x）的解是方程|x﹣ |﹣1=0 的解，求 a 的值． 【解析】解：方程|x﹣ |﹣1=0 的解为：x= 或 x=﹣ ， 把 x= 代入方程 ax+2=2（a+x）得： a+2=2（a+ ）， 解得：a=﹣2 把 x=﹣ 代入方程 ax+2=2（a+x）得： a+2=2（a﹣ ）， 解得：a= ，综上可得，a=﹣2 或 a= 例 3、解方程： （1）2﹣ =x﹣ （2）2[ x﹣（ x﹣ ）]= x 5 （3）|4x﹣3|﹣2=3x+4 （4）|x﹣|2x+1||=3 【解析】（1）x=1 （2）x= （3）x=﹣ 或 x=9 （4））x=﹣ 或 x=2 考点三：一元一次方程的应用 例 1、如图是一根可伸缩的鱼竿，鱼竿是用 10 节大小不同的空心套管连接而成．闲置时鱼竿可收缩，完全 收缩后，鱼竿长度即为第 1 节套管的长度（如图 1 所示）：使用时，可将鱼竿的每一节套管都完全拉伸（如 图 2 所示）．图 3 是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图．已知第 1 节套管长 50cm，第 2 节套管长 46cm，以此类推，每一节套管均比前一节套管少 4cm．完全拉伸时，为了使相邻两节套管连接并 固定，每相邻两节套管间均有相同长度的重叠，设其长度为 xcm． （1）请直接写出第 5 节套管的长度； （2）当这根鱼竿完全拉伸时，其长度为 311cm，求 x 的值 【解 析】解：（1）第 5 节套管的长 度为： 50﹣4×（5﹣1）=34（cm） （2）第 10 节套管的长度为： 50﹣4×（10﹣1）=14（cm）， 设每相邻两节套管间重叠的长度为 xcm，根据题意得： （50+46+42+…+14）﹣9x=311 解得：x=1 答：每相邻两节套管间重叠的长度为 1cm 6 例 2、如图，将一张正方形铁片的 4 个角剪去 4 个大小一样的小正方形，然后折起来就可以制成一个无盖的 长方体容器，设这个正方形铁片的边长为 a，做成的无盖长方体容器高为 h （1）用含 a 和 h 的代数式表示出这个无盖长方体容器的容积 V； （2）若 a=12cm，h=2cm，则做成的无盖长方体容器的容积是多少？ （3）在（2）中做成的无盖长方体容器中注满水，再把水全部倒入一个底面直径为 8cm 的圆柱形容器内， 请问该圆柱形容器的高度至少是多少？（π取 3.14，结果精确到 0.1cm） 【解析】（1）设这个正方形铁片的边长为 a，做成的无盖长方体容器高为 h， ∴容器底面是一个正方形，其边长为 a﹣2h， ∴这个无盖长方体容器的容积 V=（a﹣2h）2h； （2）若 a=12cm，h=2cm，则 V=（12﹣2×2）2×2=128cm3； （3）设该圆柱形容器的高度为 xcm，根据题意得 3.14×（ ）2×x=128 解得 x=2.5 答：该圆柱形容器的高度至少是 2.5cm 例 3、列方程解应用题 某市为提倡节约用水，采取分段方式收费．若每户每月用水不超过 22m3，则每立方米收费 a 元，若每户每 月用水超过 22m3，则超过部分每立方米加收 1.1 元． （1）小张家 12 月用水 10m3，共交水费 23 元，求 a 的值； （2）老王家 12 月份共交水费 71 元，问老王家 12 月用水多少 m3？ 【解析】解：（1）由题意得：10a=23，解得：a=2.3， （2）设老王家 12 月用水 x m3，根据题意可得： 22×2.3+（2.3+1.1）（x﹣22）=71 解得：x=28， 答：老王家 12 月用水 28m3 例 4、甲、乙两地相距 720km，一列快车和一列慢车都从甲地驶往乙地，慢车先行驶 1 小时后，快车才开始 行驶．已知快车的速度是 120km/h，慢车的速度是 80km/h，快车到达乙地后，停留了 20min，由于有新的 任务，于是立即按原速返回甲地．在快车从甲地出发到回到甲地的整个程中，与慢车相遇了两次，这两次 相遇时间间隔是多少？ 7 【解析】解：设从甲地驶往乙地时，快车行驶 x 小时追上慢车，由题意得 120x=80（x+1） 解得 x=2 则慢车行驶了 3 小时 设在整个程中，慢车行驶了 y 小时，则快车行驶了（y﹣1﹣ ）小时，由题意得 120（y﹣1﹣ ）+80y=720×2 解得 y=8 8﹣3=5（小时） 答：在快车从甲地出发到回到甲地的整个程中，与慢车相遇了两次，这两次相遇时间间隔是 5 小时 例 5、有一个水池，用两根水管注水，如果单开甲管，5 小时注满水池，如果单开乙管，10 小时注满水池． （1）如果甲先注水 2 小时，然后由甲、乙共同注水，还需要多少时间才能把水池注满？ （2）假设在水池下面安装了排水管丙管，单开丙管 6 小时可以把一满池水放完，如果三管同时开放，多少 小时才能把一空池注满水？ 【解析】解：（1）设这个水池的体积为单位“1”，设甲、乙共同注水，还需要 x 小时才能把水池注满 根据题意得： +（ + ）x=1 解得：x=2 答：甲、乙共同注水，还需要 2 小时才能把水池注满； （2）设三管同时开放，a 小时才能把一空池注满水，根据题意得： （ + ﹣ ）a=1 解得：a= 答：三管同时开放， 小时才能把一空池注满水 例 6、某商场因换季，将一品牌服装打折销售，每件服装如果按标价的六折出售将亏 10 元，而按标价的七 五折出售将赚 17 元，问： （1）每件服装的标价是多少元？ （2）每件服装的成本是多少元？ 8 （3）为保证不亏本，最多能打几折？(保留一位小数) 【解析】根据同一件衣服进价是相等的，这一等量关系列方程解答。 解：（1）设每件服装的标价是 x 元， 由题意得：60%x+10=75%x﹣17 解得：x=180 所以，每件衣服的标价为 180 元 （2）每件服装的成本是：60%×180+10=118（元） （3）为保证不亏本，设最多能打 y 折，由题意得： 180× =118 解得：y≈6.6 所以，为了保证不亏本，最多可以打 6.6 折 答：每件服装的标价为 400 元，每件衣服的成本价是 250 元，为保证不亏本，最多能打 6.6 折 例 7、如图，数轴上 A，B 两点对应的有理数分别为 10 和 15，点 P 从点 A 出发，以每秒 1 个单位长度的速 度沿数轴正方向运动，点 Q 同时从原点 O 出发，以每秒 2 个单位长度的速度沿数轴正方向运动，设运动时 间为 t 秒． （1）当 0＜t＜5 时，用含 t 的式子填空：BP= ，AQ= ； （2）当 t=2 时，求 PQ 的值； （3）当 PQ= 时，求 t 的值 【解析】解：（1）∵当 0＜t＜5 时，P 点对应的有理数为 10+t＜15，Q 点对应的有理数为 2t＜10， ∴BP=15﹣（10+t）=5﹣t，AQ=10﹣2t． （2）当 t=2 时，P 点对应的有理数为 10+2=12，Q 点对应的有理数为 2×2=4， 所以 PQ=12﹣4=8； （3）∵t 秒时，P 点对应的有理数为 10+t，Q 点对应的有理数为 2t， ∴PQ=|2t﹣（10+t）|=|t﹣10|， ∵PQ= ， ∴|t﹣10|=2.5， 解得 t=12.5 或 7.5 9 P(Practice-Oriented)——实战演练 实战演练  课堂狙击 1、方程（a+2）x2+5xm﹣3﹣2=3 是一元一次方程，则 a 和 m 分别为（ ） A．2 和 4 B．﹣2 和 4 C．2 和﹣4 D．﹣2 和﹣4 【解析】解：根据分析可得：a+2=0 且 m﹣3=1 解得：a=﹣2，m=4 故选 B 2、若方程（m2-4m+3）x|m|﹣3=0 是一元一次方程，则 m 的值为 ． 【解析】解：∵方程（m2-4m+3）x|m|﹣3=0 是一元一次方程 ∴|m|=1 且 m2-4m+3≠0 则 m=±1，将±1 分被带入 m2-4m+3， 当 m=1 时 m2-4m+3=0，舍去 当 m=-1 时 m2-4m+3=8，保留 故 m=﹣1 3、a、b、c 三个物体的重量如下图所示： 回答下列问题： （1）a、b、c 三个物体就单个而言哪个最重？ （2）若天平一边放一些物体 a，另一边放一些物体 c，要使天平平衡，天平两边至少应该分别放几个物体 a 和物体 c？ 【解析】解：（1）根据图示知：2a=3b，2b=3c． ∴a= b，b= c， ∴a= c， ∵ c＞ c＞c， ∴a＞b＞c；∴a、b、c 三个物体就单个而言，a 最重； （2）由（1）知，a= c 10 ∴4a=9c ∴若天平一边放一些物体 a，另一边放一些物体 c，要使天平平衡，天平两边至少应该分别放 4 个物体 a 和 9 个物体 c 4、数学迷小虎在解方程 ﹣1 去分母时，方程右边的﹣1 漏乘了 3，因而求得方程的解为 x= -5， 请你帮小虎同学求出 a 的值，并且正确求出原方程的解 【解析】解：按小虎的解法，解方程得 x=a，又因为小虎解得 x=﹣5，所以 a=﹣5 把 a=﹣5 代入原方程得到方程： 2 1 5 13 3 x x   ，解得 x= -7，即正确解方程得到 x=﹣7 5、解方程： （1） （2）x﹣3（ ）=2（x+2） （3） ﹣ =1 （4） （5） = （6）|x﹣1|+|x﹣5|=4 【解析】含绝对值方程，根据分类讨论，可化简去掉绝对值，根据解方程，可得答案 （1）x=1.4 （2）x=﹣5 （3）x= （4）x=﹣3 （5）x=1.5 或 2.5 （6）1≤x≤5 6、某产品供应商为了促进该产品的销售，同意给商场供货时将该产品的供货价格降低 5%，而该产品的商 场零售价不变，这样一来，该产品商场零售时的单位利润率由原来的 x%提高到（x+10）%，则 x 的值为多 少？ 【解析】售价没有变，这是解题的等量关系。 解：设原来的供货价格为 a 元，根据题意可得： 11 a（1﹣5%）[1+（x+10）%]=a×（1+x%）， 解得：x= 90 答：x 的值为 90 7、一个两位数，个位上的数字比十位上的数字小 8，且个位上的数字与十位上的数字的和比这个两位数的 小 3，求这个两位数 【解析】解：设十位上的数字为 x，则个位上的数字为（x-8），由题意，得 x+x-8= [10x+（x-8）]-3 解得：x=9 则个位上的数字为：9-8=1，所以这个两位数为 91 答：这个两位数为 91 8、一列“动车组”高速列车和一列普通列车的车身长分别为 80 米与 100 米，它们相向行驶在平行的轨道上， 若坐在高速列车上的旅客看见普通列车驶过窗口的时间是 5 秒，则坐在普通列车上的旅客看见高速列车驶 过窗口的时间是（ ） A．7.5 秒 B．6 秒 C．5 秒 D．4 秒 【解析】注意两车相向而行，速度为两车的速度之和，路程为静止的人看到的车长 解：设坐在普通列车上的旅客看见高速列车驶过窗口的时间是 x 秒，则 100÷5×x=80， 解得 x=4 故选 D 9、一件风衣，按成本价提高 50%后标价，后因季节关系按标价的 8 折出售，每件卖 180 元，这件风衣的成 本价是（ ） A．150 元 B．80 元 C．100 元 D．120 元 【解析】解：设这件风衣的成本价为 x 元 x×（1+50%）×80%=180 解得 x=150 故选 A 10、2016 年 4 月 21 日在深圳体育馆召开的第八届中国（深圳）国际茶业文化博览会上某茶商将甲、乙两种 茶叶卖出，甲种茶叶卖出 1200 元，盈利 20%，乙种茶叶卖出 1200 元，亏损 20%，则此人在这次交易中是 12 （ ） A．盈利 50 元 B．盈利 100 元 C．亏损 150 元 D．亏损 100 元 【解析】解：设甲种茶叶的买价是 x 元，根据题意得： （1+20%）x=1200 解得 x=1000 设乙种茶叶的买价是 y 元，根据题意得： （1﹣20%）y=1200 解得 y=1500 1000+1500＞1200+1200 即此次交易中亏损了 100 元，故选 D  课后反击 1、已知关于 x 的方程 的一元一次方程，试求 a bx  【解析】解：根据题意，得 b﹣2=1，且 a=0 解得 b=3，a=0； ∴关于 x 的方程是 5+ x=0 解得，x=﹣10 ∴ a bx  =﹣1000 2、已知（m2﹣1）x2﹣（m+1）x+8=0 是关于 x 的一元一次方程，求代数式 199（m+x）（x﹣2m）+3m+15 的值 【解析】解：根据题意得： ，解得：m=1， 则方程是：﹣2x+8=0， 解得：x=4，则原式=199（1+4）（4﹣2）+3+15=2008 3、已知 5x2﹣5x﹣3=7，利用等式的性质，求 2x2﹣2x+3 的值 【解析】2x2﹣2x+3=7 13 4、解方程： （1） （2） （3） （5） 2|x﹣2|+|x+1|=|3x﹣3| （6）|x﹣4| ﹣|x+2|=x+3 【解析】去绝对值符号，分情况讨论 （1）x= （2）x=1 （3）x= （4）x=﹣38 （5）x≤﹣1 或 x≥2 （6）x=﹣ 5、一种商品售价为 120 元，由于购买的人多，商家便提价 25%销售，但提价后，商品滞销，商家只好再降 价 x%，使商品恢复到原价，那么 x%=（ ） A．25 B．20 C．25% D．20% 【解析】由题意则有： 120（1+25%）（1﹣x%）=120 x%=20% 故选 D 6、一列匀速前进的火车，从它进入 320 米长的隧道到完全通过隧道共用了 18 秒，隧道顶部一盏固定的小 灯灯光在火车上照了 10 秒钟，则这列火车的长为（ ） A．190 米 B．400 米 C．380 米 D．240 米 【解析】解：设这列火车的长为 x 米，根据题意得： = 解得：x=400 故选：B 7、一件工程，甲独做要 40 天，乙独做要 60 天，现在两人合做，中间甲因病休息了几天，所以 27 天才完 成，甲休息了多少天？ 菁优网版 权所有 （4） 14 【解析】将这项工程的总量当做单位“1”， 设甲休息了 x 天，依题意则有： 1 1(27 ) 27 140 60x    解得 x=5 答：甲休息了 5 天 8、运动会前夕，爸爸陪小明在 400m 的环形跑道上训练， 他们在同一地点沿着同一方向同时出发 （1）请根据他们的对话内容，求出小明和爸爸的速度； （2）爸爸追上小明后，在第二次相遇前，再经过 分钟，小明和爸爸在跑道上相距 50m 【解析】解：（1）设爸爸的速度为 x m/min，则小明的速度为 m/min， 根据题意得： 解得：x=400 = 答：小明的速度为 300 m/min，爸爸的速度为 400 m/mim （2）50÷（400﹣300）=50÷100=0.5（分钟） （400﹣50）÷（400﹣300）=350÷100=3.5（分钟） 答：再经过 0.5 或 3.5 分钟，小明和爸爸在跑道上相距 50m 故答案为：0.5 或 3.5． 9、如图 1，长方形 OABC 的边 OA 在数轴上，O 为原点，长方形 OABC 的面积为 12，OC 边长为 3 （1）数轴上点 A 表示的数为 （2）将长方形 OABC 沿数轴水平移动，移动后的长方形记为 O′A′B′C′，移动后的长方形 O′A′B′C′与原长方 形 OABC 重叠部分（如图 2 中阴影部分）的面积记为 S． ① 当 S 恰好等于原长方形 OABC 面积的一半时，数轴上点 A′表示的数为 ． ② 设点 A 的移动距离 AA′=x． ⅰ．当 S=4 时，x= ； ⅱ．D 为线段 AA′的中点，点 E 在线段 OO′上，且 OE= OO′，当点 D，E 所表 示的数互为相反数时，求 x 的值 15 【解析】解：（1）∵长方形 OABC 的面积为 12，OC 边长为 3， ∴OA=12÷3=4 ∴数轴上点 A 表示的数为 4，故答案为：4 （2）① ∵S 恰好等于原长方形 OABC 面积的一半， ∴S=6 ∴O′A=6÷3=2 当向左运动时，如图 1，A′表示的数为 2 当向右运动时，如图 2 ∵O′A′=AO=4 ∴OA′=4+4﹣2=6 ∴A′表示的数为 6 故答案为：6 或 2 ②ⅰ．如图 1，由题意得：CO•OA′=4 ∵CO=3 ∴OA′= ∴x=4﹣ = 故答案为： ⅱ．如图 1，当原长方形 OABC 向左移动时，点 D 表示的数为 ，点 E 表示的数为 ， 由题意可得方程：4﹣ x﹣ x=0 解得：x= 如图 2，当原长方形 OABC 向右移动时，点 D，E 表示的数都是正数，不符合题意 16 直击中考 1、【2015 深圳】下表为深圳市居民每月用水收费标准，（单位：元/m3）。 用水量 单价 22x a 剩余部分 1.1a （1）某用户用水 10 立方米，公交水费 23 元，求 a 的值； （2）在（1）的前提下，该用户 5 月份交水费 71 元，请问该用户用水多少立方米？ 【解析】（1）由题意，10a=23,解得 a=2.3 (2)设用户用水量为 x 立方米，用水量为 22 立方米时，水费为 22×2.3=50.6＜71，故 x＞22 依题意则有：22×2.3+（x-22）×(2.3+1.1)=71 解得 x=28 答：该用户用水 28 立方米 2、【2012 梧州】今年 5 月，在中国武汉举办了汤姆斯杯羽毛球团体赛．在 27 日的决赛中，中国队占胜韩 国队夺得了冠军．某羽毛球协会组织一些会员到现场观看了该场比赛．已知该协会购买了每张 300 元和每 张 400 元的两种门票共 8 张，总费用为 2700 元．请问该协会购买了这两种门票各多少张？ 【解析】设每张 300 元的门票买了 x 张，则每张 400 元的门票买了（8﹣x）张，由题意，得 300x+400（8﹣x）=2700 解得：x=5 ∴买 400 元每张的门票张数为：8﹣5=3 张． 答：每张 300 元的门票买了 5 张，每张 400 元的门票买了 3 张 S(Summary-Embedded)——归纳总结 重点回顾 一、打折销售问题 1、打折销售相关概念： ①成本价：即进价，商店进货时的价格；②标价：在商店出售时所标明的价格； ③售价：商品出售时的实际价格； ④利润率：商品的利润与成本价的比值。 17 ⑤折数：打 n 折，表示为按原价的 10 n 出售，另外，像打七五折，是按原价的 7.5 10 出售，以此类推，打九五 折，就是按原价的 9.5 10 出售。 2、与打折销售有关的公式： ①利润=售价-成本（进价） ②利润率=利润÷成本价×100% ③售价=成本价+利润=成本价×（1+利润率） ④售价=标价×打折数 二、行程问题 1、相遇问题，它的特点是相向而行，这类问题一般画出示意图帮助分析题意。这类问题的等量关系一般 是：双方所走路程之和=全部路程，这只是常见的等量关系，解题时还需结合实际分析等量关系。 2、追及问题，它的特点是同向而行，等量关系一般是：双方路程之差=原来双方相距的路程。这只是常 见的等量关系，解题时还需结合实际分析等量关系。 3、航行问题：顺水速度=船在静水中的速度+水流速度 逆水速度=船在的静水中速度-水流速度 名师点拨 1、解决实际问题一般步骤 学霸经验  本节课我学到了  我需要努力的地方是