- 911.50 KB
- 2021-10-25 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
北师七年级(上)期末数学试卷1
一、选择题(本大题共10个小题,每小题3分,共30分)
1.(3分)﹣的相反数是( )
A.﹣2 B.2 C.﹣ D.
2.(3分)下列运算正确的是( )
A.2a+3b=5a+b B.2a﹣3b=﹣(a﹣b) C.2a2b﹣2ab2=0 D.3ab﹣3ba=0
3.(3分)已知2x3y2与﹣x3my2的和是单项式,则式子4m﹣24的值是( )
A.20 B.﹣20 C.28 D.﹣2
4.(3分)若2(a+3)的值与4互为相反数,则a的值为( )
A.﹣1 B.﹣ C.﹣5 D.
5.(3分)解方程4(x﹣1)﹣x=2(x+)步骤如下:①去括号,得4x﹣4﹣x=2x+1;②移项,得4x+x﹣2x=4+1;③合并同类项,得3x=5;④化系数为1,x=.从哪一步开始出现错误( )
A.① B.② C.③ D.④
6.(3分)由若干个相同的小正方体组合而成的一个几何体的三视图如图所示,则组成这个几何体的小正方形个数是( )
A.3 B.4 C.5 D.6
7.(3分)下列画图的语句中,正确的为( )
A.画直线AB=10cm
B.画射线OB=10cm
C.延长射线BA到C,使BA=BC
D.过直线AB外一点画一条直线和直线AB相交
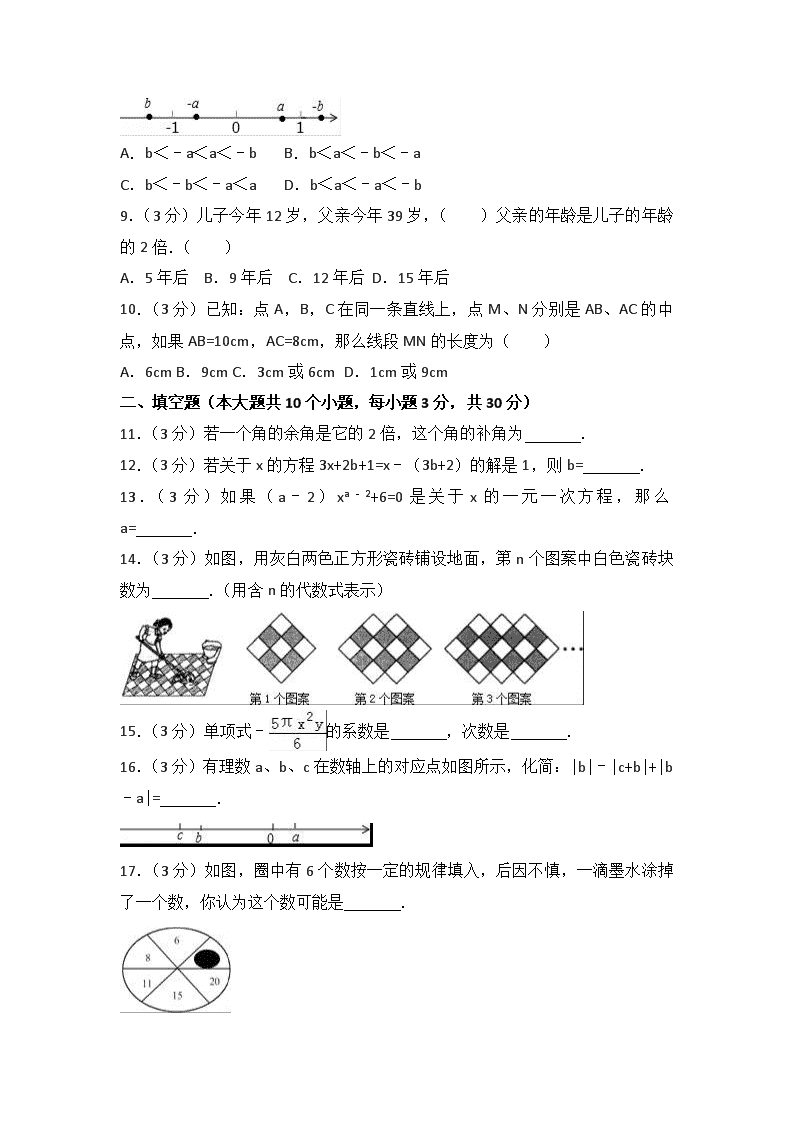
8.(3分)有理数,a、b在数轴上的位置如图所示,则a、b、﹣b、﹣a的大小关系是( )
A.b<﹣a<a<﹣b B.b<a<﹣b<﹣a
C.b<﹣b<﹣a<a D.b<a<﹣a<﹣b
9.(3分)儿子今年12岁,父亲今年39岁,( )父亲的年龄是儿子的年龄的2倍.( )
A.5年后 B.9年后 C.12年后 D.15年后
10.(3分)已知:点A,B,C在同一条直线上,点M、N分别是AB、AC的中点,如果AB=10cm,AC=8cm,那么线段MN的长度为( )
A.6cm B.9cm C.3cm或6cm D.1cm或9cm
二、填空题(本大题共10个小题,每小题3分,共30分)
11.(3分)若一个角的余角是它的2倍,这个角的补角为 .
12.(3分)若关于x的方程3x+2b+1=x﹣(3b+2)的解是1,则b= .
13.(3分)如果(a﹣2)xa﹣2+6=0是关于x的一元一次方程,那么a= .
14.(3分)如图,用灰白两色正方形瓷砖铺设地面,第n个图案中白色瓷砖块数为 .(用含n的代数式表示)
15.(3分)单项式﹣的系数是 ,次数是 .
16.(3分)有理数a、b、c在数轴上的对应点如图所示,化简:|b|﹣|c+b|+|b﹣a|= .
17.(3分)如图,圈中有6个数按一定的规律填入,后因不慎,一滴墨水涂掉了一个数,你认为这个数可能是 .
18.(3分)如图,C,D,E是线段AB上的三个点,下面关于线段CE的表示:
①CE=CD+DE; ②CE=BC﹣EB;
③CE=CD+BD﹣AC; ④CE=AE+BC﹣AB.
其中正确的是 (填序号).
三、解答题(共40分)
19.(8分)计算
(1)(﹣)×(﹣30);
(2)1÷(﹣1)+0÷4﹣5×0.1×(﹣2)3.
20.(8分)解方程
(1)3(x+2)﹣1=x﹣3;
(2)﹣1=.
21.(8分)先化简,再求值:
(4x2﹣4y2)﹣3(x2y2+x2)+3(x2y2+y2),其中x=﹣1,y=2.
22.(8分)用大小两台拖拉机耕地,每小时共耕地30亩.已知大拖拉机的效率是小拖拉机的1.5倍,问小拖拉机每小时耕地多少亩?
23.(14分)如图,P是线段AB上一点,AB=12cm,C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上),运动的时间为ts.
(1)当t=1时,PD=2AC,请求出AP的长;
(2)当t=2时,PD=2AC,请求出AP的长;
(3)若C、D运动到任一时刻时,总有PD=2AC,请求出AP的长;
(4)在(3)的条件下,Q是直线AB上一点,且AQ﹣BQ=PQ,求PQ的长.
参考答案与试题解析
一、选择题(本大题共10个小题,每小题3分,共30分)
1.(3分)﹣的相反数是( )
A.﹣2 B.2 C.﹣ D.
【解答】解:根据相反数的含义,可得
﹣的相反数是:﹣(﹣)=.
故选:D.
2.(3分)下列运算正确的是( )
A.2a+3b=5a+b B.2a﹣3b=﹣(a﹣b) C.2a2b﹣2ab2=0 D.3ab﹣3ba=0
【解答】解:A、2a、3b不是同类项,不能合并,此选项错误;
B、2a﹣3b=﹣(a﹣b),此选项错误;
C、2a2b、﹣2ab2不是同类项,不能合并,此选项错误;
D、3ab﹣3ba=0,此选项正确;
故选:D
3.(3分)已知2x3y2与﹣x3my2的和是单项式,则式子4m﹣24的值是( )
A.20 B.﹣20 C.28 D.﹣2
【解答】解:由题意可知:2x3y2与﹣x3my2是同类项,
∴3=3m,
∴m=1,
∴4m﹣24=4﹣24=﹣20,
故选(B)
4.(3分)若2(a+3)的值与4互为相反数,则a的值为( )
A.﹣1 B.﹣ C.﹣5 D.
【解答】解:∵2(a+3)的值与4互为相反数,
∴2(a+3)+4=0,
∴a=﹣5,
故选C
5.(3分)解方程4(x﹣1)﹣x=2(x+)步骤如下:①去括号,得4x﹣4﹣x=2x+1;②移项,得4x+x﹣2x=4+1;③合并同类项,得3x=5;④化系数为1,x=.从哪一步开始出现错误( )
A.① B.② C.③ D.④
【解答】解:方程4(x﹣1)﹣x=2(x+)步骤如下:①去括号,得4x﹣4﹣x=2x+1;②移项,得4x﹣x﹣2x=4+1;③合并同类项,得x=5;④化系数为1,x=5.
其中错误的一步是②.
故选B.
6.(3分)由若干个相同的小正方体组合而成的一个几何体的三视图如图所示,则组成这个几何体的小正方形个数是( )
A.3 B.4 C.5 D.6
【解答】解:综合三视图,我们可以得出,这个几何模型的底层有3+1=4个小正方体,第二有1个小正方体,
因此搭成这个几何体模型所用的小正方体的个数是4+1=5个.
故选:C.
7.(3分)下列画图的语句中,正确的为( )
A.画直线AB=10cm
B.画射线OB=10cm
C.延长射线BA到C,使BA=BC
D.过直线AB外一点画一条直线和直线AB相交
【解答】解:A、错误.直线没有长度;
B、错误.射线没有长度;
C、错误.射线有无限延伸性,不需要延长;
D、正确.
故选D.
8.(3分)有理数,a、b在数轴上的位置如图所示,则a、b、﹣b、﹣a的大小关系是( )
A.b<﹣a<a<﹣b B.b<a<﹣b<﹣a C.b<﹣b<﹣a<a D.b<a<﹣a<﹣b
【解答】解:根据图示,可得
b<﹣a<a<﹣b.
故选:A.
9.(3分)儿子今年12岁,父亲今年39岁,( )父亲的年龄是儿子的年龄的2倍.( )
A.5年后 B.9年后 C.12年后 D.15年后
【解答】解:设x年后父亲的年龄是儿子的年龄的2倍,
根据题意得:39+x=2(12+x),
解得:x=15.
答:15年后父亲的年龄是儿子的年龄的2倍.
故选D.
10.(3分)已知:点A,B,C在同一条直线上,点M、N分别是AB、AC的中点,如果AB=10cm,AC=8cm,那么线段MN的长度为( )
A.6cm B.9cm C.3cm或6cm D.1cm或9cm
【解答】解:(1)点C在线段AB上,如:
点M是线段AB的中点,点N是线段BC的中点,
MB=AB=5,BN=CB=4,
MN=BM﹣BN=5﹣4=1cm;
(2)点C在线段AB的延长线上,如:
点M是线段AB的中点,点N是线段BC的中点,
MB=AB=5,BN=CB=4,
MN=MB+BN=5+4=9cm,
故选:D.
二、填空题(本大题共10个小题,每小题3分,共30分)
11.(3分)若一个角的余角是它的2倍,这个角的补角为 150° .
【解答】解:设这个角为x°,则它的余角为(90﹣x)°,
90﹣x=2x
解得:x=30,
180°﹣30°=150°,
答:这个角的补角为150°,
故答案为:150°.
12.(3分)若关于x的方程3x+2b+1=x﹣(3b+2)的解是1,则b= ﹣1 .
【解答】解:把x=1代入方程3x+2b+1=x﹣(3b+2)得:3+2b+1=1﹣(3b+2),
解得:b=﹣1,
故答案为:﹣1.
13.(3分)如果(a﹣2)xa﹣2+6=0是关于x的一元一次方程,那么a= 3 .
【解答】解:∵(a﹣2)xa﹣2+6=0是关于x的一元一次方程,
∴a﹣2=1,
解得:a=3,
故答案为:3.
14.(3分)如图,用灰白两色正方形瓷砖铺设地面,第n个图案中白色瓷砖块数为 2+3n .(用含n的代数式表示)
【解答】解:观察图形发现:
第1个图案中有白色瓷砖5块,
第2个图案中白色瓷砖多了3块,
依此类推,
第n个图案中,白色瓷砖是5+3(n﹣1)=3n+2.
15.(3分)单项式﹣的系数是 ﹣ ,次数是 3 .
【解答】解:∵单项式﹣的数字因数是﹣,所有字母指数的和=2+1=3,
∴此单项式的系数是﹣,次数是3.
故答案为:﹣,3.
16.(3分)有理数a、b、c在数轴上的对应点如图所示,化简:|b|﹣|c+b|+|b﹣a|= ﹣b+c+a .
【解答】解:由数轴可知:c<b<0<a,
∴b<0,c+b<0,b﹣a<0,
∴原式=﹣b+(c+b)﹣(b﹣a)=﹣b+c+b﹣b+a=﹣b+c+a,
故答案为:﹣b+c+a
17.(3分)如图,圈中有6个数按一定的规律填入,后因不慎,一滴墨水涂掉了一个数,你认为这个数可能是 26或5 .
【解答】解:∵按逆时针方向有8﹣6=2;11﹣8=3;15﹣11=4;
∴这个数可能是20+6=26或6﹣1=5.
18.(3分)如图,C,D,E是线段AB上的三个点,下面关于线段CE的表示:
①CE=CD+DE; ②CE=BC﹣EB;
③CE=CD+BD﹣AC; ④CE=AE+BC﹣AB.
其中正确的是 ①②④ (填序号).
【解答】解:如图,①CE=CD+DE,故①正确;
②CE=BC﹣EB,故②正确;
③CE=CD+BD﹣BE,故③错误;
④∵AE+BC=AB+CE,
∴CE=AE+BC﹣AB=AB+CE﹣AB=CE,故④正确;
故答案是:①②④.
三、解答题(共40分)
19.(8分)计算
(1)(﹣)×(﹣30);
(2)1÷(﹣1)+0÷4﹣5×0.1×(﹣2)3.
【解答】解:(1)原式=﹣10+2=﹣8;
(2)原式=﹣1+0﹣0.5×(﹣8)
=﹣1+4
=3.
20.(8分)解方程
(1)3(x+2)﹣1=x﹣3;
(2)﹣1=.
【解答】解:(1)去括号,得:3x+6﹣1=x﹣3,
移项,得:3x﹣x=﹣3﹣6+1,
合并同类项,得:2x=﹣8,
系数化为1,得:x=﹣4;
(2)去分母,得:3(x+1)﹣6=2(2﹣x),
去括号,得:3x+3﹣6=4﹣2x,
移项,得:3x+2x=4+6﹣3,
合并同类项,得:5x=7,
系数化为1,得:x=.
21.(8分)先化简,再求值:
(4x2﹣4y2)﹣3(x2y2+x2)+3(x2y2+y2),其中x=﹣1,y=2.
【解答】解:(4x2﹣4y2)﹣3(x2y2+x2)+3(x2y2+y2)
=4x2﹣4y2﹣3x2y2﹣3x2+3x2y2+3y2
=x2﹣y2,
当x=﹣1,y=2时,原式=(﹣1)2﹣22=﹣3.
22.(8分)用大小两台拖拉机耕地,每小时共耕地30亩.已知大拖拉机的效率是小拖拉机的1.5倍,问小拖拉机每小时耕地多少亩?
【解答】解:设小拖拉机每小时耕地x亩,则大拖拉机每小时耕地(30﹣x)亩,
根据题意得:30﹣x=1.5x,
解得:x=12.
答:小拖拉机每小时耕地12亩.
23.(14分)如图,P是线段AB上一点,AB=12cm,C、D两点分别从P、B
出发以1cm/s、2cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上),运动的时间为ts.
(1)当t=1时,PD=2AC,请求出AP的长;
(2)当t=2时,PD=2AC,请求出AP的长;
(3)若C、D运动到任一时刻时,总有PD=2AC,请求出AP的长;
(4)在(3)的条件下,Q是直线AB上一点,且AQ﹣BQ=PQ,求PQ的长.
【解答】解:(1)根据C、D的运动速度知:BD=2,PC=1,
则BD=2PC,
∵PD=2AC,
∴BD+PD=2(PC+AC),即PB=2AP,
∵AB=12cm,AB=AP+PB,
∴12=3AP,则AP=4cm;
(2)根据C、D的运动速度知:BD=4,PC=2,
则BD=2PC,
∵PD=2AC,
∴BD+PD=2(PC+AC),即PB=2AP,
∵AB=12cm,AB=AP+PB,
∴12=3AP,则AP=4cm;
(3)根据C、D的运动速度知:BD=2PC
∵PD=2AC,
∴BD+PD=2(PC+AC),即PB=2AP,
∴点P在线段AB上的处,即AP=4cm;
(4)如图:
∵AQ﹣BQ=PQ,
∴AQ=PQ+BQ;
又∵AQ=AP+PQ,
∴AP=BQ,
∴PQ=AB=4cm;
当点Q'在AB的延长线上时,
AQ′﹣AP=PQ′,
所以AQ′﹣BQ′=PQ=AB=12cm.
综上所述,PQ=4cm或12cm.
北师七年级(上)期末数学试卷2
一、选择题:(本大题10小题,每小题4分,共40分.每小题给出的四个选项中,只有一个选项是符合题意的,请将该选项的标号填入表格内)
1.(4分)的倒数是( )
A. B. C. D.
2.(4分)过度包装既浪费资源又污染环境.据测算,如果全国每年减少10%的过度包装纸用量,那么可减排二氧化碳3120000吨,把数3120000用科学记数法表示为( )
A.3.12×105 B.3.12×106 C.31.2×105 D.0.312×107
3.(4分)如果∠A的补角与∠A的余角互补,那么2∠A是( )
A.锐角 B.直角
C.钝角 D.以上三种都可能
4.(4分)若与kx﹣1=15的解相同,则k的值为( )
A.8 B.2 C.﹣2 D.6
5.(4分)如图是由几个相同的正方体搭成的一个几何体,从正面看到的平面图形是( )
A. B. C. D.
6.(4分)下列各题中,合并同类项结果正确的是( )
A.2a2+3a2=5a2 B.2a2+3a2=6a2 C.4xy﹣3xy=1 D.2m2n﹣2mn2=0
7.(4分)有理数a,b在数轴上的表示如图所示,则下列结论中:①ab<0,②ab>0,
③a+b<0,④a﹣b<0,⑤a<|b|,⑥﹣a>﹣b,正确的有( )
A.2个 B.3个 C.4个 D.5个
8.(4分)下列各题中正确的是( )
A.由7x=4x﹣3移项得7x﹣4x=3
B.由=1+去分母得2(2x﹣1)=1+3(x﹣3)
C.由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1
D.由2(x+1)=x+7 移项、合并同类项得 x=5
9.(4分)在下列调查中,适宜采用普查的是( )
A.了解我省中学生的视力情况
B.了解九(1)班学生校服的尺码情况
C.检测一批电灯泡的使用寿命
D.调查台州《600全民新闻》栏目的收视率
10.(4分)将全体自然数按下面的方式进行排列:
按照这样的排列规律,2019应位于( )
A.位 B.位 C.位 D.位
二、填空题:(每小题4分,共24分)
11.(4分)单项式﹣πa3bc的次数是 ,系数是 .
12.(4分)若有理数a、b满足|a﹣5|+(b+7)2=0,则a+b的值为 .
13.(4分)若代数式x﹣y的值为4,则代数式2x﹣3﹣2y的值是 .
14.(4分)近似数6.4×105精确到 位.
15.(4分)|x﹣1|=1,则x= .
16.(4分)已知线段AB=6cm,点C在直线AB上,且CA=4cm,O是AB的中点,则线段OC的长度是 cm.
三、解答题:(共86分)
17.(8分)计算:﹣23﹣×[2﹣(﹣3)2].
18.(8分)化简
(1)3x﹣2x2+5+3x2﹣2x﹣5;
(2)2(2a﹣3b)+3(2b﹣3a).
19.(8分)如图,已知平面上有四个点A,B,C,D.
(1)连接AB,并画出AB的中点P;
(2)作射线AD;
(3)作直线BC与射线AD交于点E.
20.(8分)解方程:x﹣=﹣.
21.(10分)化简求值:3(x2﹣2xy)﹣(2x2﹣xy),其中x=2,y=3.
22.(10分)苏宁电器元旦促销,将某品牌彩电按进价提高40%,然后在广告上写“元旦大酬宾,八折优惠”,结果每台彩电仍获利270元,那么每台彩电进价是多少元?
23.(10分)如图,已知线段AD=6cm,线段AC=BD=4cm,E,F分别是线段AB,CD的中点,求EF的长度.
24.(12分)某中学为了丰富学生的校园体育锻炼生活,决定根据学生的兴趣爱好采购一批体育用品供学生课后锻炼使用,
因此学校随机抽取了部分同学就兴趣爱好进行调查,将
收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
(1)设学校这次调查共抽取了n名学生,求出n的值;
(2)请你补全条形统计图;
(3)求出乒乓球和羽毛球所对圆心角的度数;
(4)设该校共有学生1200名,请你估计该校有多少名学生喜欢跳绳?
25.(12分)如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB=90°,∠BOC=60°时,∠MON的度数是多少?为什么?
(2)如图2,当∠AOB=70°,∠BOC=60°时,∠MON= (直接写出结果).
(3)如图3,当∠AOB=α,∠BOC=β时,猜想:∠MON= (直接写出结果).
参考答案与试题解析
一、选择题:(本大题10小题,每小题4分,共40分.每小题给出的四个选项中,只有一个选项是符合题意的,请将该选项的标号填入表格内)
1.(4分)的倒数是( )
A. B. C. D.
【解答】解:﹣1=﹣,
∵(﹣)×(﹣)=1,
∴﹣1的倒数是﹣.
故选:C.
2.(4分)过度包装既浪费资源又污染环境.据测算,如果全国每年减少10%的过度包装纸用量,那么可减排二氧化碳3120000吨,把数3120000用科学记数法表示为( )
A.3.12×105 B.3.12×106 C.31.2×105 D.0.312×107
【解答】解:将3120000用科学记数法表示为:3.12×106.
故选:B.
3.(4分)如果∠A的补角与∠A的余角互补,那么2∠A是( )
A.锐角 B.直角
C.钝角 D.以上三种都可能
【解答】解:由题意得
(90°﹣∠A)+(180°﹣∠A)=180°
解得2∠A=90°.
故选:B.
4.(4分)若与kx﹣1=15的解相同,则k的值为( )
A.8 B.2 C.﹣2 D.6
【解答】解:先解方程得:
x=8;
把x=8代入kx﹣1=15得:
8k=16,
k=2.
故选:B.
5.(4分)如图是由几个相同的正方体搭成的一个几何体,从正面看到的平面图形是( )
A. B. C. D.
【解答】解:从正面看第一层是三个小正方形,第二层在中间位置一个小正方形,故D符合题意,
故选:D.
6.(4分)下列各题中,合并同类项结果正确的是( )
A.2a2+3a2=5a2 B.2a2+3a2=6a2 C.4xy﹣3xy=1 D.2m2n﹣2mn2=0
【解答】解:A、2a2+3a2=5a2,正确;
B、2a2+3a2=5a2,错误;
C、4xy﹣3xy=xy,错误;
D、原式不能合并,错误,
故选:A.
7.(4分)有理数a,b在数轴上的表示如图所示,则下列结论中:①ab<0,②ab>0,
③a+b<0,④a﹣b<0,⑤a<|b|,⑥﹣a>﹣b,正确的有( )
A.2个 B.3个 C.4个 D.5个
【解答】解:根据数轴上点的位置得:b<0<a,且|a|<|b|,
可得ab<0,a+b<0,a﹣b>0,a<|b|,﹣a<﹣b,
则正确的有3个,
故选:B.
8.(4分)下列各题中正确的是( )
A.由7x=4x﹣3移项得7x﹣4x=3
B.由=1+去分母得2(2x﹣1)=1+3(x﹣3)
C.由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1
D.由2(x+1)=x+7 移项、合并同类项得 x=5
【解答】解:A、7x=4x﹣3移项,得7x﹣4x=﹣3,故选项错误;
B、由=1+去分母,两边同时乘以6得2(2x﹣1)=6+3(x﹣3),选项错误;
C、2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x+9=1,故选项错误;
D、由2(x+1)=x+7 去括号得2x+2=x+7,
移项,2x﹣x=7﹣2,
合并同类项得 x=5,故选项正确.
故选:D.
9.(4分)(2017秋•永新县期末)在下列调查中,适宜采用普查的是( )
A.了解我省中学生的视力情况
B.了解九(1)班学生校服的尺码情况
C.检测一批电灯泡的使用寿命
D.调查台州《600全民新闻》栏目的收视率
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似判断即可.
【解答】解:A、了解我省中学生的视力情况,调查范围广,适合抽样调查,故A错误;
B、了解九(1)班学生校服的尺码情况适合普查,故B正确;
C、检测一批电灯泡的使用寿命,调查具有破坏性,适合抽样调查,故C错误;
D、调查台州《600全民新闻》栏目的收视率,调查范围广,适合抽样调查,故D错误;
故选:B.
【点评】本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
10.(4分)将全体自然数按下面的方式进行排列:
按照这样的排列规律,2019应位于( )
A.位 B.位 C.位 D.位
【解答】解:由图可知,每4个数为一个循环组依次循环,
∵2019是第2020个数,
∴2020÷4=505,
∴2019应位于第505循环组的第1个数,在位.
故选:D.
二、填空题:(每小题4分,共24分)
11.(4分)单项式﹣πa3bc的次数是 5 ,系数是 π .
【解答】解:单项式﹣πa3bc的次数是5,系数是.
故答案为:5,﹣.
12.(4分)若有理数a、b满足|a﹣5|+(b+7)2=0,则a+b的值为 ﹣2 .
【解答】解:∵|a﹣5|+(b+7)2=0,
∴a﹣5=0,b+7=0,
∴a=5,b=﹣7;
因此a+b=5﹣7=﹣2.
故答案为:﹣2.
13.(4分)若代数式x﹣y的值为4,则代数式2x﹣3﹣2y的值是 5 .
【解答】解:由题意得:x﹣y=4,
则原式=2(x﹣y)﹣3=8﹣3=5.
故答案为:5
14.(4分)近似数6.4×105精确到 万 位.
【解答】解:6.4×105精确到万位.
故答案为万.
15.(4分)|x﹣1|=1,则x= 2或0 .
【解答】解:∵|x﹣1|=1,
∴x﹣1=±1,
∴x=2或0,
故答案为:2或0.
16.(4分)已知线段AB=6cm,点C在直线AB上,且CA=4cm,O是AB的中点,则线段OC的长度是 1或7 cm.
【解答】解:如图1所示,
∵线段AB=6cm,O是AB的中点,
∴OA=AB=×6cm=3cm,
∴OC=CA﹣OA=4cm﹣3cm=1cm.
如图2所示,
∵线段AB=6cm,O是AB的中点,CA=4cm,
∴OA=AB=×6cm=3cm,
∴OC=CA+OA=4cm+3cm=7cm
故答案为:1或7.
三、解答题:(共86分)
17.(8分)计算:﹣23﹣×[2﹣(﹣3)2].
【解答】解:﹣23﹣×[2﹣(﹣3)2]
=﹣8﹣×(2﹣9)
=﹣8﹣×(﹣7)
=﹣8﹣(﹣1)
=﹣8+1
=﹣7.
18.(8分)化简
(1)3x﹣2x2+5+3x2﹣2x﹣5;
(2)2(2a﹣3b)+3(2b﹣3a).
【解答】解:(1)3x﹣2x2+5+3x2﹣2x﹣5[
=(3x﹣2x)+(﹣2x2+3x2)+(5﹣5)
=x2+x;
(2)2(2a﹣3b)+3(2b﹣3a)
=4a﹣6b+6b﹣9a
=﹣5a.
19.(8分)如图,已知平面上有四个点A,B,C,D.
(1)连接AB,并画出AB的中点P;
(2)作射线AD;
(3)作直线BC与射线AD交于点E.
【解答】解:由题意可得,如右图所示.
20.(8分)解方程:x﹣=﹣.
【解答】解:去分母得6x﹣3(x﹣1)=4﹣(x+2),
去括号得6x﹣3x+3=4﹣x﹣2
移项合并得4x=﹣1,
系数化为1得x=﹣.
21.(10分)化简求值:3(x2﹣2xy)﹣(2x2﹣xy),其中x=2,y=3.
【解答】解:原式=3x2﹣6xy﹣2x2+xy
=x2﹣5xy,
当x=2,y=3时,原式=22﹣5×2×3=﹣26.
22.(10分)苏宁电器元旦促销,将某品牌彩电按进价提高40%,然后在广告上写“元旦大酬宾,八折优惠”,结果每台彩电仍获利270元,那么每台彩电进价是多少元?
【解答】解:设每台彩电进价是x元,
依题意得:0.8(1+40%)x﹣x=270,
解得:x=2250.
答:每台彩电进价是2250元.
23.(10分)如图,已知线段AD=6cm,线段AC=BD=4cm,E,F分别是线段AB,CD的中点,求EF的长度.
【解答】解:∵E,F分别是线段AB,CD的中点,
∴AB=2EB=2AE,CD=2CF=FD,
∵AD=AB+BC+CD=2EB+BC+2CF=6,AC=2EB+BC=4,
∴AC+2CF=6,
解得,CF=1,
同理可得:EB=1,
∴BC=2,
∴EF=EB+BC+CF=1+2+1=4.
24.(12分)某中学为了丰富学生的校园体育锻炼生活,决定根据学生的兴趣爱好采购一批体育用品供学生课后锻炼使用,
因此学校随机抽取了部分同学就兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
(1)设学校这次调查共抽取了n名学生,求出n的值;
(2)请你补全条形统计图;
(3)求出乒乓球和羽毛球所对圆心角的度数;
(4)设该校共有学生1200名,请你估计该校有多少名学生喜欢跳绳?
【分析】(1)根据喜欢篮球的人数有25人,占总人数的25%即可得出总人数;
(2)根据总人数求出喜欢羽毛球的人数,补全条形统计图即可;
(3)360°乘以对应百分比可得;
(4)喜欢跳绳的人数占总人数的20%乘以总人数即可得出结论.
【解答】解:(1)本次调查的总人数n=10÷10%=100;
(2)羽毛球的人数为100×20%=20人,
补全条形图如下:
(3)乒乓球所对应圆心角度数为360°×25%=90°,羽毛球所对应圆心角度数为360°×20%=72°;
(4)1200×20%=240,
答:估计该校有240名学生喜欢跳绳.
【点评】本题考查的是条形统计图,熟知从条形图可以很容易看出数据的大小,便于比较是解答此题的关键.
25.(12分)如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB=90°,∠BOC=60°时,∠MON的度数是多少?为什么?
(2)如图2,当∠AOB=70°,∠BOC=60°时,∠MON= 35° (直接写出结果).
(3)如图3,当∠AOB=α,∠BOC=β时,猜想:∠MON= α (直接写出结果).
【解答】解:(1)如图1,∵∠AOB=90°,∠BOC=60°,
∴∠AOC=90°+60°=150°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=∠AOC=75°,∠NOC=∠BOC=30°
∴∠MON=∠MOC﹣∠NOC=45°.
(2)如图2,
∵∠AOB=70°,∠BOC=60°,
∴∠AOC=70°+60°=130°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=∠AOC=65°,∠NOC=∠BOC=30°
∴∠MON=∠MOC﹣∠NOC=65°﹣30°=35°.
故答案为:35°.
(3)如图3,∠MON=α,与β的大小无关.
理由:∵∠AOB=α,∠BOC=β,
∴∠AOC=α+β.
∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠MOC=∠AOC=(α+β),
∠NOC=∠BOC=β,
∴∠AON=∠AOC﹣∠NOC=α+β﹣β=α+β.
∴∠MON=∠MOC﹣∠NOC
=(α+β)﹣β=α
即∠MON=α.
故答案为:α.
北师七年级(上)期末数学试卷3
第一部分 选择题
一. 选择题(每小题3分)
1. 下列选项中,比小的数是( )
A. B. C. D.
2. 第14届中国(深圳)国际茶产业博览会在深圳会展中心展出一只如图所示的紫砂壶,从不同方向看这只紫砂壶,你认为是从上面看到的效果图是( )
3. 下列各式符合代数式书写规范的是( )
A. B. C. 元 D.
4.2017年12月11日,深圳证券交易所成功招标发行深圳轨道交通专项债劵,用来建设地铁14号线,该项目估算资金总额约为39500000000元,将39500000000元用科学计数法表示为( )
A. 元 B.元 C. 元 D.元
5. 下列计算正确的是( )
A. B. C. D.
6. 如图所示,能用∠AOB,∠O,∠1三种方法表示同一个角的图形的是( )
7. 现实生活中“为何有人乱穿马路,却不愿从天桥或斑马线通过?”,请用数学知识解释图中这一现象,其原因为( )
A. 两点之间线段的长度,叫做这两点之间的距离
B. 过一点有无数条直线
C. 两点确定一条直线
D. 两点之间,线段最短
8. 深圳市12月上旬每天平均空气质量指数(AQI)分别为:35,42,55,78,57,64,58,69,74,82,
为了描述这十天空气质量的变化情况,最适合用的统计图是( )
A. 折线统计图 B.频数直方图 C.条形统计图 D.扇形统计图
星期一
星期二
星期三
星期四
星期五
星期六
星期日
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
5. 如图,AB=24,点C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )
A.12 B.18
C.16 D.20
6. 若是方程的解,则的值为( )
A.10 B.4 C.3 D.-3
7. 在如图所示的2018年元月份的月历表中,任意框出表中竖列上四个数,这四个数的和可能是( )
A.86 B.78 C.60 D.101
8. 下列叙述:①最小的正整数是0;②的系数是;③用一个平面去截正方体,截面不可能是六边形;④若AC=BC,则点C是线段AB的中点;⑤三角形是多边形;⑥绝对值等于本身的数是正数,其中正确的个数有( )
A.2 B.3 C.4 D.5
二、 填空题(每小题3分)
9. 已知和是同类项,则式子的值是 .
10. 在数轴上,与表示数的点的距离是三个单位长度的点表示的数是 .
11. 某书店把一本新书按标价的八折出售,仍获利30%,若该书的进价为40元,则标价为 元.
16.如图所示的运算程序中,若开始输入的值为,我们发现第1次输出的结果为48,第2次输出的结果为24,……,第2018次输出的结果为 .
三、解答题
17.(本题15分)计算:
(1)
(2)
(3)
18.(本题4分)先化简,再求值:
其中a=.
19.(本题8分)解方程
(1)
(2) (2)
20.(本题8分)为了解某校学生对A 《最强大脑》、B 《朗读者》、 C 《中国诗词大会》、D《出彩中国人》四个电视节目的喜爱情况,随机抽取了m学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下两幅不完整的统计图(如图1和图2):
根据统计图提供的信息,回答下列问题;
(1) m= ,n= ;
(2) 扇形统计图中,喜爱《最强大脑》节目所对应的扇形的圆心角读书是 度.
(3) 根据以上信息直接在答题卡中补全条形统计图;
(4)根据抽样调查的结果,请你估计该校6000名学生中有多少学生最喜欢《中国诗词大会》节目.
21.(本题5分):如图,∠AOC=∠BOC=50°,OD平分∠AOB,求∠AOB和∠
COD的度数.
22.(本题5分)深圳某小区停车场的收费标准如下:中型汽车的停车费为15元/辆,小型汽车的停车费为10元/辆.现在停车场有50辆中、小型汽车,期中中型汽车有x辆.
(1)则小型汽车的车辆数为 (用含x的代数式表示)
(2)这些车共缴纳停车费580元,求中、小型汽车各有多少辆?
23.(本题8分)如图,在数轴上点A表示的数a、点B表示数b,a、b满足|a-30|+(b+6)2=0.点O是数轴原点.
(1)点A表示的数为 __,点B表示的数为 ,线段AB的长为 .
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=2BC,则点C在数轴上表示的数为 .
(3)现有动点P、Q都从B点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到O点时,点Q才从B点出发,并以每秒3个单位长度的速度向右移动,且当点P到达A点时,点Q就停止移动,设点P移动的时间为t秒,问:当t为多少时,P、Q两点相距4个单位长度?
参考答案