北师大版七年级上册-第08讲-有理数的乘方及混合运算（提高）-教案 10页

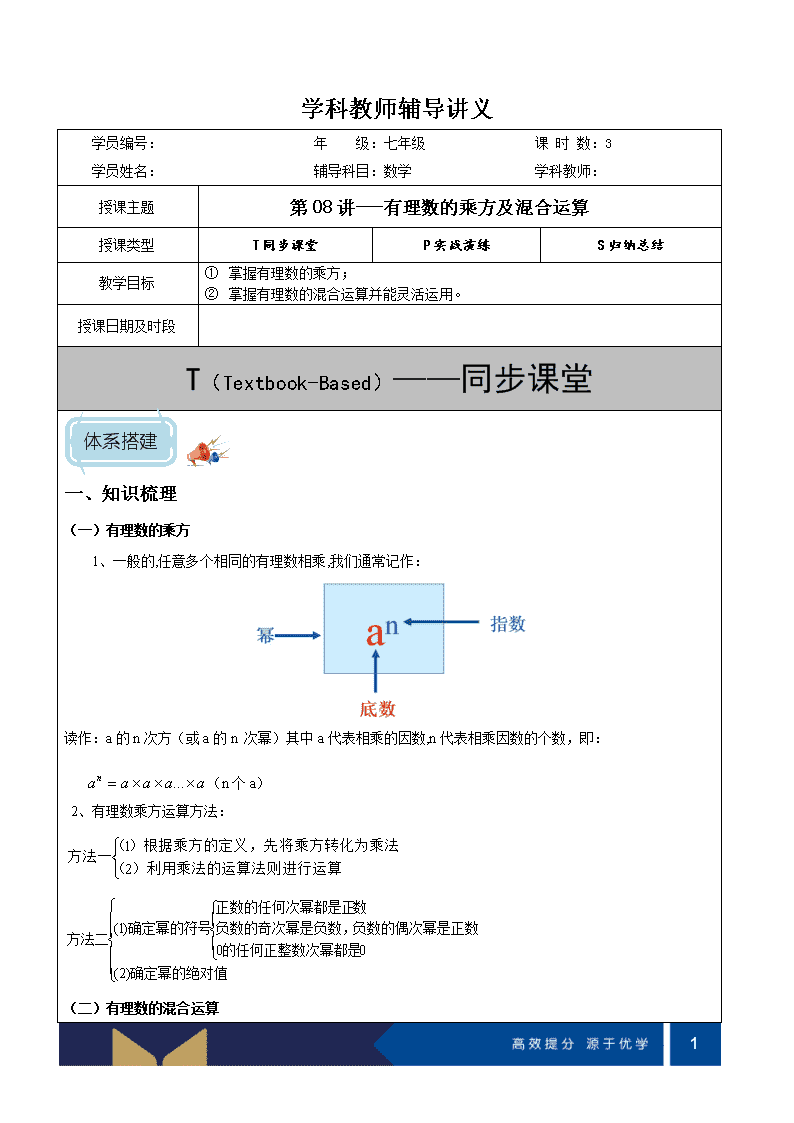
1 学科教师辅导讲义 学员编号： 年 级：七年级 课 时 数：3 学员姓名： 辅导科目：数学 学科教师： 授课主题 第 08 讲---有理数的乘方及混合运算 授课类型 T 同步课堂 P 实战演练 S 归纳总结 教学目标 1 掌握有理数的乘方； 2 掌握有理数的混合运算并能灵活运用。 授课日期及时段 T（Textbook-Based）——同步课堂 体系搭建 一、知识梳理 （一）有理数的乘方 1、一般的,任意多个相同的有理数相乘,我们通常记作： 读作：a 的 n 次方（或 a 的 n 次幂）其中 a 代表相乘的因数,n 代表相乘因数的个数，即： ... n a na a a a a    6444447444448个 （n 个 a） 2、有理数乘方运算方法：    进行运算）利用乘法的运算法则（ 将乘方转化为乘法）根据乘方的定义，先（方法一 2 1           确定幂的绝对值 的任何正整数次幂都是 负数的偶次幂是正数负数的奇次幂是负数， 数正数的任何次幂都是正 确定幂的符号方法二 )2( 00 )1( （二）有理数的混合运算 2 混合运算法则：先算乘方，再算乘除，最后算加减；如果有括号，先算括号里面的。 注意：怎样算简单，怎样算准确，是数学计算最重要的原则。 （三）科学记数法 （1）一般地，一个大于 10 的数可以表示成 10na  的形式，其中1 10a  ，n 是正整数，这种记数方 法叫做科学记数法。注意以下几点: 1、科学记数法的形式是由两个数的乘积组成的。其中一个因数为 a（1 10a  ），另一个因数为10n ， n 的值等于整数部分的位数减 1； 2、用科学记数法表示数时，不改变数的符号，只是改变数的书写形式而已。小于 1 的正数也可以用科学记 数法表示。例如： 50.00001 10 ； 典例分析 考点一：乘方的意义 例 1、 3x 表示（ ） A. x3 B． xxx  C. xxx  D． 3x 【解析】C 考点二：计算 例 1、（1） 3 2 11      （2）  33 131  （3）  342 554 14      （4）      332 20132  【解析】 1、 8 27 2、2 3、－59 4、－1 考点三：定义新运算 例 1、现规定一种新的运算“※”： a ※ abb  ，如 3※2= 32 =8，则 3※ 等于（ ） A． B． 8 C． D． 【解析】A 考点四：偶次幂的非负性 3 例 1、若   021 2  ba ，则  2012ba  的值是（ ） A．﹣1 B． 1 C． 0 D． 2012 【解析】B 例 2、已知     0532 22  cba ，求 22 cba  值． 【解析】33 考点五：有理数的混合运算 例 1、计算：（1）      342810 2  （2）          9 163249 2 【解析】（1）-20；（2）23 考点六：科学计数法 例 1、自贡市统计局 2016 年初发布了 2015 年我市经济形势：2015 年全市地区生产总值（GDP）实现 1143.11 亿元．数据 1143.11 亿元用科学记数法表示（保留三个有效数字）（ ） A、1.14×103 元 B、1.14×1010 元 C、1.14×1011 元 D、1.14×1012 元 【解析】C 例 2、在“十二•五”期间，达州市经济保持稳步增长，地区生产总值约由 819 亿元增加到 1351 亿元，年均增 长约 10%，将 1351 亿元用科学记数法表示应为（ ） A、1.351×1011 B、13.51×1012 C、1.351×1013 D、0.1351×1012 【解析】A 例 3、在日本核电站事故期间，我国某监测点监测到极微量的人工放射性核素碘﹣131，其浓度为 0.000 0963 贝克/立方米．数据“0.000 0963”用科学记数法可表示为（ ） A、9.63×10﹣5 B、96.3×10﹣6 C、0.963×10﹣5 D、963×10﹣4 【解析】A 例 4、地球绕太阳公转的速度用科学记数法表示为 1.1×105km/h，把它写成原数是（ ） A 、1100000km/h B、 110000km/h C、 11000km/h D、 0.000011km/h 【解析】B 考点七：综合题 4 例 1、如图是某种细胞分裂示意图，这种细胞每过 30 分钟便由 1 个分裂成 2 个．根据此规律可得： （1）这样的一个细胞经过第四个 30 分钟后可分裂成 个细胞； （2）这样的一个细胞经过 3 小时后可分裂成 个细胞； （3）这样的一个细胞经过 n（n 为正整数）小时后可分裂成 个细胞． 【解析】（1）16；（2）64；（3） n22 例 2、【2011•黔南州】观察下列算式：21=2，22=4，23=8，24=16，…．根据上述算式中 的规律，请你猜想 210 的末位数字是（ ） A． 2 B． 4 C． 8 D． 6 【解析】B 例 3、王老师为调动学生参加班级活动的积极性，给每位学生设计了一个如图所示的面积为 1 的圆形纸片， 若在活动中表现优胜者，可依次用色彩纸片覆盖圆面积的 ， ， …．请你根据数 形结合的思想，依据图形的变化，推断当 n 为整数时，  n2 1...8 1 4 1 2 1 _____________． 【解析】 n2 11 P(Practice-Oriented)——实战演练 实战演练  课堂狙击 1、数学上一般把  anaaaaa 个..... 记为（ ） A． na B． an  C． na D． an 【解析】C 2、计算：   22 3232 （ ） A.0 B.-54 C.-72 D.-18 5 【解析】A 3、下列式子中正确的是（ ） A.    324 222  B.    243 222  C.    234 222  D.     432 232  【解析】C 4、某地今年 1 月 1 日至 4 日每天的最高气温与最低气温如下表： 日期 1 月 1 日 1 月 2 日 1 月 3 日 1 月 4 日 最高气温 5℃ 4℃ 0℃ 4℃ 最低气温 0℃ -2℃ -4℃ -4℃ A.1 月 1 日 B.1 月 2 日 C.1 月 3 日 D.1 月 4 日 【解析】D 5、生物学指出：生态系统中，每输入一个营养级的能量，大约只有 10%的能量能够流动到下一个营养级， 在 H1→H2→H3→H4→H5→H6 这条生物链中（Hn 表示第 n 个营养级，n=1，2，…，6），要使 H6 获得 10 千 焦的能量，那么需要 H1 提供的能量约为（ ） A． 104 千焦 B． 105 千焦 C． 106 千焦 D． 107 千焦 【解析】C 6、我国平均每平方千米的土地一年从太阳得到的能量，相当于燃烧 130 000 000kg 的煤所产生的能量．把 130 000 000kg 用科学记数法可表示为（ ） A、13×107kg B、0.13×108kg C、1.3×107kg D、1.3×108kg 【解析】D 7、一种细菌的半径是 0.000045 米，该数字用科学记数法表示正确的是（ ） A、4.5×105 B、45×106 C、4.5×10﹣5 D、4.5×10﹣4 【解析】C 8、PM2.5 是指大气中直径小于或等于 2.5×10﹣3 毫米的颗粒物，也称为可入肺颗粒物，把 2.5×10﹣3 用小数形 式表示正确的是（ ） 6 A、0.000025 B、0.00025 C、0.0025 D、0.025 【解析】C 9、-9、6、-3 三个数的和比它们绝对值的和小_______。 【解析】24 10、两个有理数之积是 1，已知一个数是 7 12 ，则另一个数是_____。 【解析】 15 7 11、计算：（1）     332 2222  （2）        7 21322 246    2 2 3 3185 2532      【解析】（1）2； （2）－73； （3）-54 12、若 2b 与  21a 互为相反数，求 ba  的值． 【解析】3 13、水葫芦是一种水生飘浮植物，有着惊人的繁殖能力．据报道，现已造成某些流域河道堵塞，水质污染 等严重后果、据研究表明：适量的水葫芦生长对水质的净化是有利的，关键是科学管理和转化利用．若在 适宜条件下， 1 株水葫芦每 5 天就能新繁殖 1 株 （不考虑植株死亡、被打捞等其它因素）． （1）假设江面上现有 1 株水葫芦，填写下表： 第几天 5 10 15 … 50 … 5n 总株数 2 4 … … （2）假定某流域内水葫芦维持在约 33 万株以内对净化水质有益．若现有 10 株水葫芦，请你尝试利用计算 器进行估算探究，照上述生长速度，多少天时水葫芦约有 33 万株？此后就必须开始定期打捞处理水葫芦．（要 求写出必要的尝试、估算过程！） 【解析】（1）8,1024， n2 （2）当 n=15 时，  万33210 16  ，故 5n=75（天） （3） 7  课后反击 1、计算：   322 32  的结果是（ ） A.-21 B.35 C.-35 D.-29 【解析】D 2、  65 表示的意义是（ ） A.6 个-5 相乘的积 B.-5 乘以 6 的积 C.5 个-6 相乘的积 D.6 个-5 相加的和 【解析】A 3、2011 年 8 月 12 日，第 26 届世界大学生夏季运动会将在深圳开幕．本届大运会的开幕式举办场地和主要 分会场深圳湾体育中心总建筑面积达 256520m2．数据 256520m2 用科学记数法（保留三个有效数字）表示 为（ ） A、2.565×105m2 B、0.257×106m2 C、2.57×105m2 D、25.7×104m2 【解析】C 4、国家卫生和计划生育委员会公布 H7N9 禽流感病毒直径约为 0.0000001m，则病毒直径 0.0000001m 用科 学记数法表示为（ ）（保留两位有效数字）。 A、0.10×10﹣6m B、1×10﹣7m C、1.0×10﹣7m D、0.1×10﹣6m 【解析】C 5、下列各数对中，数值相等的是（ ） A. 32 23  与 B.  33 22  与 C.  22 33  与 D.  22 2323  与 【解析】B 6、下列等式成立的是（ ） A.         77 110077 1100 B.    7710077 1100  C.   77 110077 1100  D.   7710077 1100  【解析】B 7、(某种细胞开始有 2 个，1 小时后分裂成 4 个并死去 1 个，2 小时后分裂成 6 个并死去 1 个，3 小时后分 裂成 10 个并死去 1 个，…，按此规律，5 小时后细胞存活的个数是（ ） A． 31 B． 33 C． 35 D． 37 8 【解析】B 8、如图，一根细长的绳子，沿中间对折，再沿对折后的中间对折，这样连续沿中间对折 5 次，用剪刀沿 5 次对折后的中间将绳子全部剪断，此时细绳被剪成（ ） A． 17 段 B． 32 段 C． 33 段 D． 34 段 【解析】C 9、下面一组按规律排列的数：1，2，4，8，16，…，第 2002 个数应是（ ） A． 20022 B. 122002  C． 20012 D．以上答案不对 【解析】C 10、若   023 2  nm ，则 nm 2 的值为（ ） A．﹣4 B．﹣1 C．0 D．4 【解析】B 11、一家电脑公司仓库原有电脑 100 台，一个星期调入、调出的电脑记录是：调入 38 台，调出 42 台，调 入 27 台，调出 33 台，调出 40 台，则这个仓库现有电脑________台。 【解析】50 12、小刚学习了有理数运算法则后，编写了一个计算程序，当他输入任意一个有理数时，显示屏上出现的 结果总等于所输入有理数的平方与 1 的和，当他第一次输入 2，然后又将所得结果再次输入后，显示屏上出 现的结果应是______。 【解析】26 13、图中是一幅“苹果图”，第一行有 1 个苹果，第二行有 2 个，第三行有 4 个，第四行有 8 个，…，你是否发现苹果的排列规律？猜猜看，第六行有 个苹果、第十行有 个． （可用乘方形式表示） 【解析】 95 2,2 14、喜欢吃拉面吗？拉面馆的师傅，用一根很粗的面条，把两头捏合在一起拉伸，再捏合，再拉伸，反复 几次，就把这根很粗的面条拉成了许多细的面条，如图所示，这样捏合到第 次后可拉出 128 根面 9 条． 【解析】7 15、“如果 Na x  （a＞0，a≠1），那么 x 叫做以 a 为底 N 的对数，记为 Nx alog ．”则 9 1log3 =_______. 【解析】-2 16、计算：（1）      32 4525.048 5      （2）   3 269 2 2 113 3 2      【解析】 （1）-90； （2） 4 3 17、已知   032 2  ba ，求 ba ab  的值． 【解析】1 战术指导 1、掌握有理数乘方的意义。 2、注意负数的奇次幂和偶次幂取号问题。 3、任意一个有理数的偶次幂一定为非负数。 直击中考 1、【2008•张家界】如果实数 a，b 满足   013 2  ba ，那么 ab 等于（ ） A． 1 B．﹣1 C．﹣3 D． 3 【解析】B 2、【2009•莱芜】计算 7 的正整数次幂：71=7，72=49，73=343，74=2401，75=16807，76=117649，77=823543， 78=5764801…归纳各计算结果中的个位数字规律，可得 20097 的个位数字为 ． 【解析】7 3、【2008•崇文区一模】观察下列等式：31﹣1=2，32﹣1=8，33﹣1=26，34﹣1=80，35﹣1=242，…．通过观 10 察，用你所发现的规律确定 32008﹣1 的个位数字是 ． 【解析】0 4、【2013•牡丹江】定义一种新的运算 a﹠b=ab，如 2﹠3=23=8，那么请试求（3﹠2）﹠2= ． 【解析】8。 S(Summary-Embedded)——归纳总结 重点回顾 1、有理数乘方表示的意义； 2、有理数混合运算的运算法则； 3、负数的奇次幂和偶次幂。 名师点拨 有理数的乘方和有理数的混合运算属于基础知识点，在进行运算时，要注意底数的正负性和指数的奇偶 性，这方面较为容易出错，在计算乘、除、乘方时可以选择优先确定结果的正负性，再进行计算。 学霸经验  本节课我学到了  我需要努力的地方是