华师版数学七年级下册课件-第9章-9多边形的内角和与外角和 15页

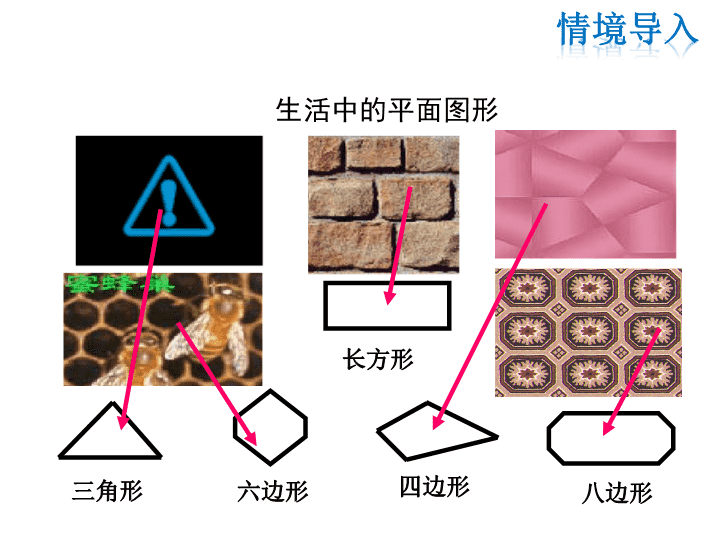
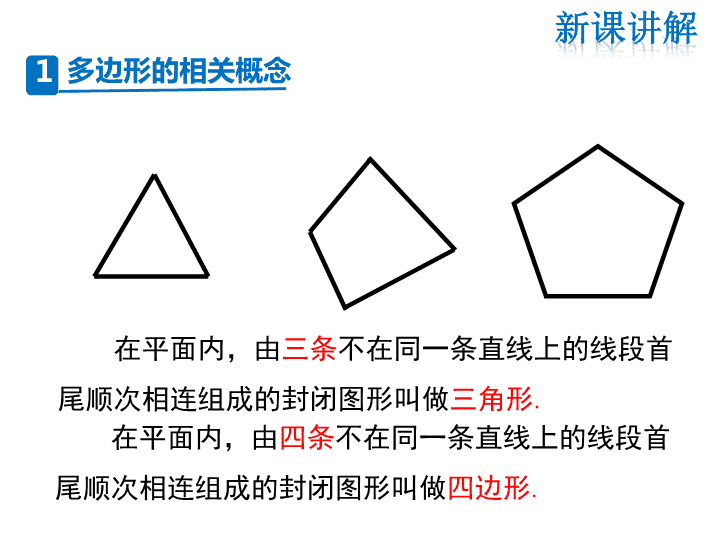
HS七(下) 教学课件 第9章 多边形 9.2 多边形的内角和与外角和 第1课时 多边形的内角和 生活中的平面图形 三角形 长方形 四边形 六边形 八边形 在平面内，由三条不在同一条直线上的线段首 尾顺次相连组成的封闭图形叫做三角形. 在平面内，由四条不在同一条直线上的线段首 尾顺次相连组成的封闭图形叫做四边形. 多边形的相关概念1 2.在平面内，由若干条不在同一条直线上的线段首尾 顺次相连组成的封闭图形叫做多边形. 1.在平面内，由五条不在同一条直线上的线段首尾顺 次相连组成的封闭图形叫做五边形. 3.组成多边形的各条线段叫作多边形的边. 4.相邻两条边的公共端点叫作多边形的顶点. 6.连接不相邻的两个顶点的线段叫作多边形的对角线. 5.相邻两边组成的角叫作多边形的内角，简称多边形 的角. 顶点 内角 边 对角线 (连接不相邻两个顶点的线段) 多边形的相关元素 外角 表示：五边形ABCDE A C B D E 2.如图1是凸多边形； 图2不是凸多边形，今后如果 不作说明，我们讲的多边形都是凸多边形. 图 2 1.如果把它任何一边双向延长，其他各边都在延长 所得直线的同一旁，这样的多边形叫做凸多边形. 图 1 A C B D A CB D 在平面内，边相等、角也都相等的多边形叫正多边形. 问题 观察下面多边形，它们的边、角有什么特点？ 特点： 各边相等，各内角都相等的多边形. 问题1 三角形的内角和等于180°，四边形的内 角和是多少度呢？ 如图，四边形ABCD的一条对 角线AC 把它分成两个三角形，因 此四边形的内角和等于这两个三角 形的内角和， 即180°×2=360°. 多边形的内角和2 在下列各个多边形中，任取一个顶点，通过该顶 点画出所有对角线，完成下表. 五边形 六边形 七边形 八边形 五边形 5 3 （5-2） × 180° 六边形 6 七边形 7 图形 边数 可分成三角形的个数 多边形的内角和 五边形 六边形 八边形 8 … … … … n边形 n 4 （6-2） × 180° （7-2） × 180°5 （8-2） × 180°6 n-2 （n-2）×180° 五边形 六边形 七边形 八边形 n边形的内角和等于(n-2)· 180°. （1）求八边形的内角和. （2）一个多边形的内角和等于2160°，求这个多 边形的边数？ 解： （1）八边形的内角和是 (8-2)×180°= 1080°. （2）设这个多边形的边数为n，则 （n-2 )×180°= 2160°， 解得n = 14. 所以这是一个十四边形. 例1 1.判断． （1）当多边形边数增加时，它的内角和也随着增加． ( ) （2）从n边形一个顶点出发，可以引出（n-2）条对角 线，得到（n-2）个三角形． ( ) 2.五边形的内角和为 ，它的对角线有 条．540° 5 180° 0° 4.一个多边形的内角和不可能是（ ） A.1800° B.540 ° C.720 ° D.810 ° D 5.一个多边形从一个顶点可引对角线3条，这个多边形 内角和等于（ ） A.360° B.540 ° C.720 ° D.900 ° C 多边形的 内角和 内角和计 算 公 式 （n-2) × 180 °(n ≥3的整数） 多边形的 相关概念