华师版数学七年级下册课件-第6章-6等式的性质与方程的简单变形 11页

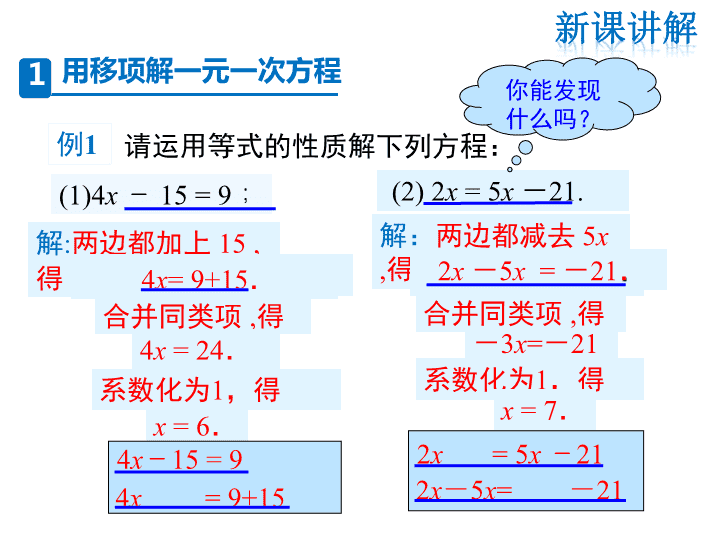
HS七(下) 教学课件 6.2.1 等式的性质与方程的简单变形 第6章 一元一次方程 第3课时 利用方程的变形求方程的解 (1)移项； 利用移项解方程的步骤： (3)系数化为1. (2)合并同类项； 请运用等式的性质解下列方程： (1)4x － 15 = 9； 解：两边都减去 5x , 得 －3x=－ 21．系数化为1，得 x = 6． 解:两边都加上 15 , 得 系数化为1，得 x = 7． 合并同类项 ,得 合并同类项 ,得 4x = 24． 2x = 5x – 214x – 15 = 9 + 15 + 15 4x－15 = 9 4x = 9+15 2x－5x= －21 4x= 9+15． 你能发现 什么吗？ 用移项解一元一次方程1 例1 4x －15 = 9 ① 4x = 9 + 15 ② 由方程① 到方程 ② , “– 15”这项移动后，发生了什么变化? 从方程的左边移到了方程的 右边. 改变了符号 4x－15 = 9 4x = 9+15 2x = 5x －21 ③ 2x －5x = －21 ④ 由方程③ 到方程 ④ , “ 5x ” 这项移动后，发生了什么变化? 改变了符号 从方程的右边移到了方程 的左边. 2x－5x= －21 解方程： .23273 xx  解：移项，得 合并同类项 ,得 3 2 32 7.x x   5 25.x  5.x  系数化为1，得 移项实际上是利 用等式的性质1， 但是解题步骤更 为简捷！ 例2 (1) 8x=2x－7; (2) 6=8+2x; 解：移项，得 8x－2x=－7, 即 6x=－7. 两边同时除以6，得 解：原方程即 8+2x=6. 移项，得 2x=－2. 两边同时除以2，得 x=－1. 解方程： 7 . 6 x   例3 (3) 1 12 3. 2 2 y y   1 12 3 2 2 y y   ， 3 5 . 2 2 y   5 . 3 y   解：移项，得 即 两边都除以 ，得 3 2 练一练 解下列方程： （1） 2.5x+318 =1068； （2） 2.4y + 2y+2.4 = 6.8. x = 300 y = 1 (1)7 2 3 4x x   (2)1.8 30 0.3t t  解下列一元一次方程： 5 4 11 8(4) 3 3 3 3 x x  xx  31 2 1)3( 答案：(1) x=-2 (2) t=20 (3) x=-4 (4) x=2 解形如“ax+b=cx+d”的方程的一般步骤： (1)移项； (2)合并同类项； (3)化未知数的系数为1.