华师版数学七年级下册课件-第10章-10轴对称的再认识 16页

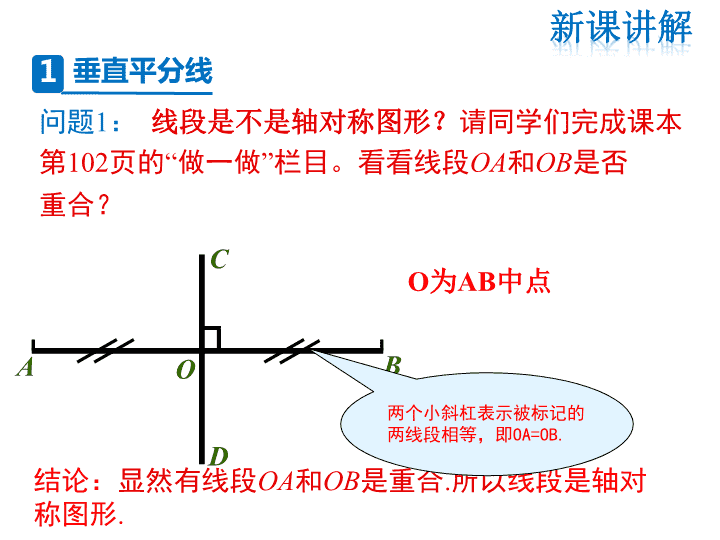
HS七(下) 教学课件 第10章 轴对称、平移与旋转 10.1 轴对称 10.1.2 轴对称的再认识 什么是轴对称图形？什么是图形成轴对称？它们 有什么共同的特征？ 问题1： 线段是不是轴对称图形？请同学们完成课 本第102页的“做一做”栏目。看看线段OA和OB是 否重合？ 结论：显然有线段OA和OB是重合.所以线段是轴对 称图形. A BO C D O为AB中点 两个小斜杠表示被标记的 两线段相等，即OA=OB. 1 垂直平分线 根据刚才的实验，我们知道线段AB是轴对称 图形。直线CD是它的对称轴。直线CD既垂直于线段 AB，又平分线AB。 定义：垂直并且平分一条线段的直线称为这条线段 垂直平分线，又叫中垂线. 概 括 问题2： 请看图，线段MA和MB会重合吗？ A BO C D O为AB中点M 分析：由于A点和B点重合，M点是同一点（公共点）， 所以线段MA和MB会重合. 线段垂直平分线的性质:线段的垂直平分线上的 点到这条线段两个端点的距离相等。 △ABC中，BC＝10，边BC的 垂直平分线分别交AB、BC于点 E、D；BE＝6，求△BCE的周长。 图 9 解：∵ED是BC的垂直平分线（已知） ∴EC＝EB=6 （线段的垂直平分线上的点到这条线段两个端点的 距离 相等） ∴△BCE的周长=BC＋CE＋EB＝10＋6＋6=22 答：△BCE的周长为22. 例1 问题2： 角是不是轴对称图形？ 试验：在半透明的纸上画∠AOB，对折，使角的 两条边完全重合，然后用直尺画出折痕OM. 从上面试验可以看出，角是轴对称图形，对 称轴是它的角平分线所在的直线. A B O P 结论：角是轴对称图形，对称轴是它的角平分线 所在的直线. 试一试：画出下列图形的对称轴. 如果没有方格子，而又不 能折叠，你还能比较准确的 画出图形的对称轴吗？ 轴对称图形的对称轴的画法 做一做 （2） （1） 1.画出下面图形的对称轴，画完图后请思考下面的 问题： ①能总结你画对称轴的方法吗？ ②连结对称点的线段与对称轴有什么关系？ 连结对称点的线段被对称轴垂直平分 2.如图，点A和点A’关于某条直线成轴对称，你能画 出这条直线吗？ A . . A’ （1）找出图形的任意一组对称点. 画图形的对称轴的画法： （2）连结对称点. （3）画出对称点所连线段的垂直平分线， 就可以得到该图形的对称轴. 结论：如果一个图形是轴对称图形，那么连结对称 点的线段的垂直平分线就是该图形的对称轴. 1.找出下面每个轴对称图形的对称轴. 2.判断题(对的在题后的括号内打“√”，错的打 “×”) (1) 线段的垂直平分线上存在到这条线段两端点 距离不相等的点 . （ ） (2) 有一公共端点的两条相等线段组成的图形是 轴对称图形 . （ ） (3) 角是轴对称图形，对称轴是角平分线. （ ） × √ × A B C 3. 如图，A、B、C三点表示三个镇的地理位置，随着乡 镇外资、集体、个体工业的发展需要，现三镇联合建 造一个变电所，要求变电所到三镇的距离相等，请你 作出变电所的位置（用点P表示） 作法： 1.分别连接AB、BC. 2.分别作线段AB、BC的垂直平分 线两直线交于点P. 则点P为所求的变电所的位置. P u线段垂直平分线的定义 经过线段中点并且垂直于这条线段的直线，叫做 这条线段的垂直平分线. 如果两个图形关于某条直线对称，那么任何一对对 称点所连线段的垂直平分线就是该图形的对称轴. u轴对称图形与垂直平分线的联系