【北师大版】七年级下册数学第四章+三角形第2节《图形的全等》参考课件2 40页

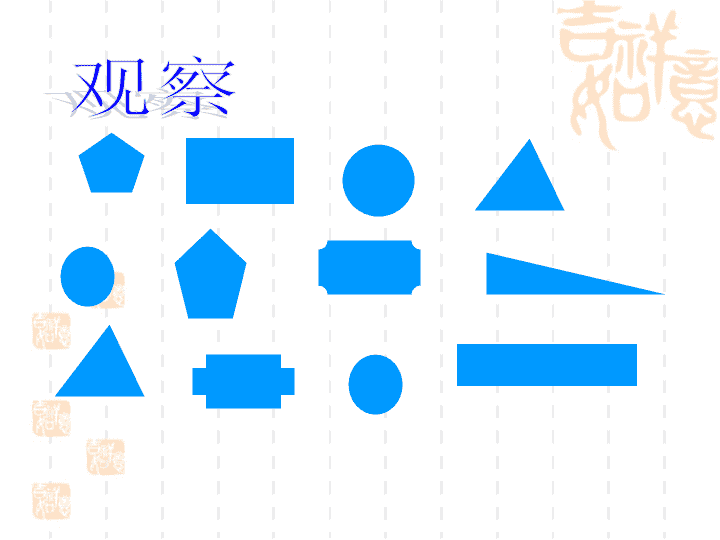
3.2 图形的全等 第三章 三角形 观察 观察 通过观察我们发现，这些图形中有些是完全一样的，如果把它们叠在一起，它们就能重合 . 能够完全重合的两个图形称为全等图形 . 全等图形 大小 不同 观察下面两组图形，它们是不是全等图形？为什么？ 练一练 形状 不同 练一练 如果两个图形全等，它们的形状和大小一定都相同 . 找出下列图形中的全等图形 练一练 沿图形中的虚线，分别把下面图形划分为两个 全等图形 . 练一练 沿图形中的虚线，分别把下面图形划分为两个 全等图形 . 练一练 与图 1 所示图形全等的图形是 图 1 A B C D 练一练 将图 2 绕 A 点顺时针转 90° 所得到的图形是 图 2 D A B C A B C 练一练 我们把能完全重合的三角形叫做全等三角形 . 你能找到图中的对应边和对应角吗？ A B C D E F 想一想 对应边： AB 与 DE,AC 与 DF,BC 与 EF 对应角：∠ A 与∠ D, ∠B 与∠ E , ∠C 与∠ F 三角形全等的表示方法 : △ABC≌△DEF A B C D E F 注意： 要把表示对应顶点的字母写在对应的位置上 . 全等三角形的对应边相等 , 对应角相等 全等三角形的性质 你能将一个等边三角形分 成两个全等三角形吗？ 能把它分成三个 , 四个 全等三角形吗？ 议一议 你能将一个等边三角形分 成两个全等三角形吗？ 能把它分成三个 , 四个 全等三角形吗？ 议一议 你能将一个等边三角形分 成两个全等三角形吗？ 能把它分成三个 , 四个 全等三角形吗？ 议一议 已知：△ ABC≌△ADC 与 BC 对应的线段： _______ 与 AD 对应的线段： _______ 与 AC 对应的线段 :________ 与∠ ACB 对应的角 :________ 与∠ B 对应的角： _________ 与 ∠ BAC 对应的角 :____________ D C B A 练一练 DC AB AC ∠ACD ∠D ∠DAC 已知：△ ACE≌△DFB 　则： 对应角有 : ________________________________ 对应边有 :_____________________ 练一练 A C B D E F AC 与 DF,AE 与 DB,CE 与 FB ∠A 与∠ D, ∠C 与∠ F, ∠AEC 与∠ DBF 如图 :△AOD≌△BOC, 写出其中相等的角 A D C B O 解：∠ A=∠B ∠D=∠C ∠DOA=∠COB 练一练 如图，已知⊿ ABD≌⊿ACE ，∠ B=∠C ，∠ ADB=∠AEC ，请用等式表示其它的对应边和对应角 . A B C D E 练一练 AB=AC AD=AE BD=CE ∠BAD=∠CAE 若 ⊿ ABE≌⊿ACD ，∠ B=∠C ，∠ ADC=∠AEB ，请用等式表示其它的对应边和对应角 . 变式训练 A B C D E AB=AC AE=AD BE=CD ∠BAE=∠CAD 如图 :△ABC≌△AEC, ∠B=30°, ∠ACB=85°, 求出△ AEC 各内角的度数 . A B C E 解： 因为△ AEC≌△ABC 所以∠ E=∠B=30° ∠ACE=∠ACB=85° ∠EAC=∠BAC=180°-30°-85°=65° 练一练 如图 ,△ABC≌△DEF,∠C=25°,BC=6cm,AC=4cm , 你能得出△ DEF 中哪些角的大小 , 哪些边的长度 ? A B C D E F 因为△ DEF≌△ABC 所以∠ F=∠C=25° EF=BC=6cm DF=AC=4cm 解： 练一练 如图 ,△ABC≌△DEF, 求证 :AD=BE B A E F C D 因为△ ABC≌△DEF 所以 AB=DE AB-BD=DE-BD 即 AD=BE 证明： 练一练 如图 ,△ABC≌△EBD, 问∠ 1 与∠ 2 相等吗 ? 若相等请证明 , 若不相等说出为什么 ? B A E 2 1 F C D O 分析： ∠ 1 与∠ 2 分别在 △ AOF 与△ EOB 中，显而 易见∠ AOF 与∠ EOB 是 对顶角，而∠ A 与∠ E 是△ ABC 与△ EBD 的对应 角，可由三角形内角和得到∠ 1 与∠ 2 相等 . 如图 ,△ABC≌△EBD, 问∠ 1 与∠ 2 相等吗 ? 若相等请证明 , 若不相等说出为什么 ? B A E 2 1 F C D O 解： 因为△ EBD≌△ABC 所以∠ A=∠E 在△ AOF 与△ EOB 中， ∠ AOF=∠EOB 根据三角形内角和为 180° 所以 ∠ 1=∠2 如图 , 若△ ABC≌△EFC, 点 B 、 C 、 E 在同一条直线 上，且 CF=3cm, CE=7cm, ∠EFC=64°, 则 BC=_____cm, AC=_____cm, ∠B=_____. B A E F C 3 64° 你还能求出哪些边的长度 , 哪些角的度数 ? 练一练 7 AF=4cm ∠ACB=∠ECF= 90° ∠ A= ∠E=26° 已知：⊿ MNP≌⊿ABC ， MN=AB ， MP=AC ，∠ MPN=35 º ，∠ CAB=40 º , 则∠ ABC=____ ，∠ M=____. 练一练 分析： 本题没有图，可以从两个角度出 发，一个是根据题意作图，另一个就是找到对应顶点 . 已知：⊿ MNP≌⊿ABC ， MN=AB ， MP=AC ，∠ MPN=35 º ，∠ CAB=40 º , 则∠ ABC=____ ，∠ M=____. 练一练 思路： 由已知 MN=AB ， MP=AC ，可以得到对应顶点分别是 M 与 A ， N 与 B,P 与 C. 由此可得： ∠ M=∠CAB=40 º ,∠ACB=∠MPN=35 º 所以∠ ABC=180 º -∠CAB-∠ACB=105 º 105 º 40 º 如图：⊿ ADC≌⊿BFE ， ∠ E=∠C ， AB=7 ， DF=3 ，求 AF 的长？ A B C E F D 练一练 A B C E F D 练一练 解： ∵⊿ADC≌⊿BFE ，∠ E=∠C ∴AD=BF ∴AD-DF=BF-DF 即 AF=BD 又∵ AF+BD=AB-DF=7-3=4(cm) ∴AF=BD ＝ 2cm 如图， ⊿ ABE≌⊿DCF ，∠ A=∠D ， BF=7cm ， CF=3cm ，求 EF 的长 . A B E F D C 变式训练 解： ∵⊿ABE≌⊿DCF ，∠ A=∠D ∴BE=CF=3cm ∴EF=BF-BE=4cm 如图 △ ABF≌△DCE ， 在三角形对应边和对应角以外，你还能得到什么结论？ Ａ Ｆ Ｅ Ｄ Ｃ Ｂ 思考 AE=DF 分析： ∵ ⊿ABF≌⊿DCE ∴AF=DE ∴AF-EF=DE-EF 即 AE=DF 如图 △ ABF≌△DCE ， 在三角形对应边和对应角以外，你还能得到什么结论？ Ａ Ｆ Ｅ Ｄ Ｃ Ｂ 思考 分析： ∵ ⊿ABF≌⊿DCE ∴ ∠AFB=∠DEC ∴ ∠AEC=∠DFB ( 等角的补角相等 ) ∠AEC=∠DFB 如图 △ ABF≌△DCE ， 在三角形对应边和对应角以外，你还能得到什么结论？ Ａ Ｆ Ｅ Ｄ Ｃ Ｂ 思考 分析： ∵ ⊿ABF≌⊿DCE ∴ ∠A=∠D ，∠ AFB=∠DEC ∴ AB∥CD ， BF∥CE （内错角相等，两直线平行） AB∥CD BF∥CE 一．你能把下面的这个平行四边形 1 ．分成两个全等的图形吗？ 思考 一．你能把下面的这个平行四边形 ２．分成四个全等的图形吗？ 思考 一．你能把下面的这个平行四边形 ３．分成三个全等的图形吗？ 思考 1. 图形的全等概念 2. 三角形全等的性质 谈谈你的收获 能够完全重合的两个图形称为全等图形 . 我们把能完全重合的三角形叫做全等三角形 . 全等三角形的对应边相等 , 对应角相等 .