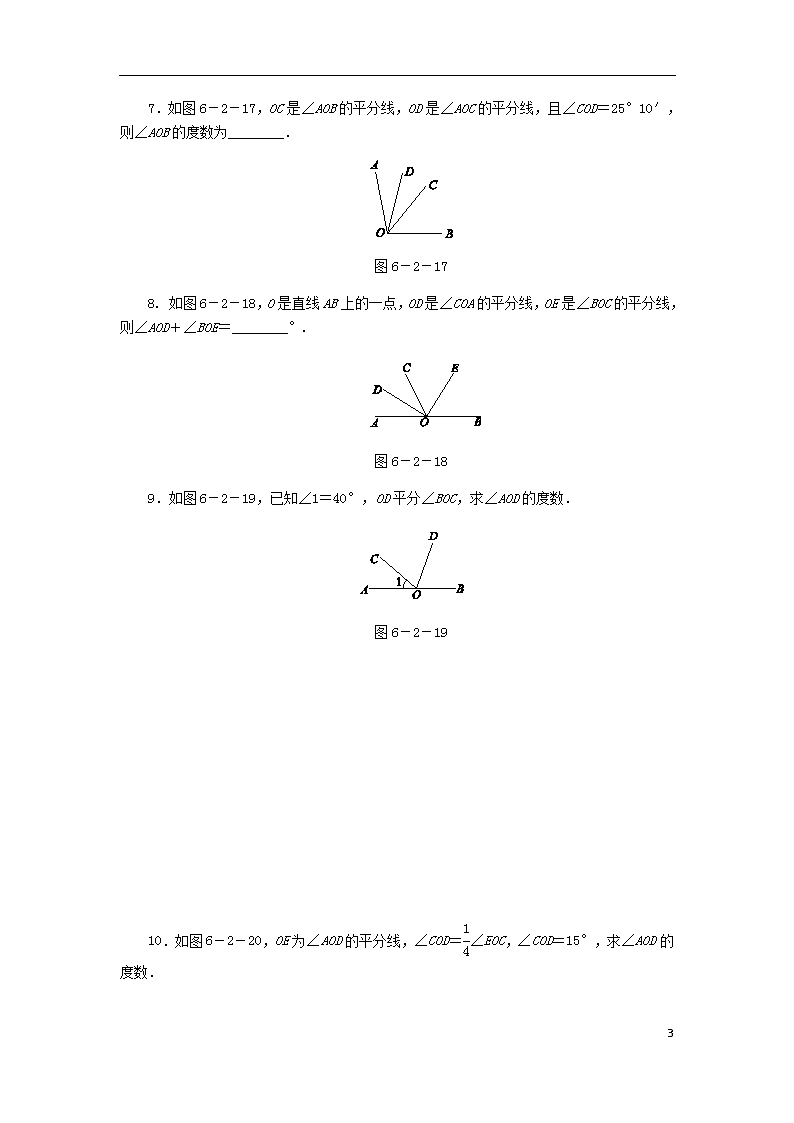2019七年级数学上册 6画角与角的平分线 10页

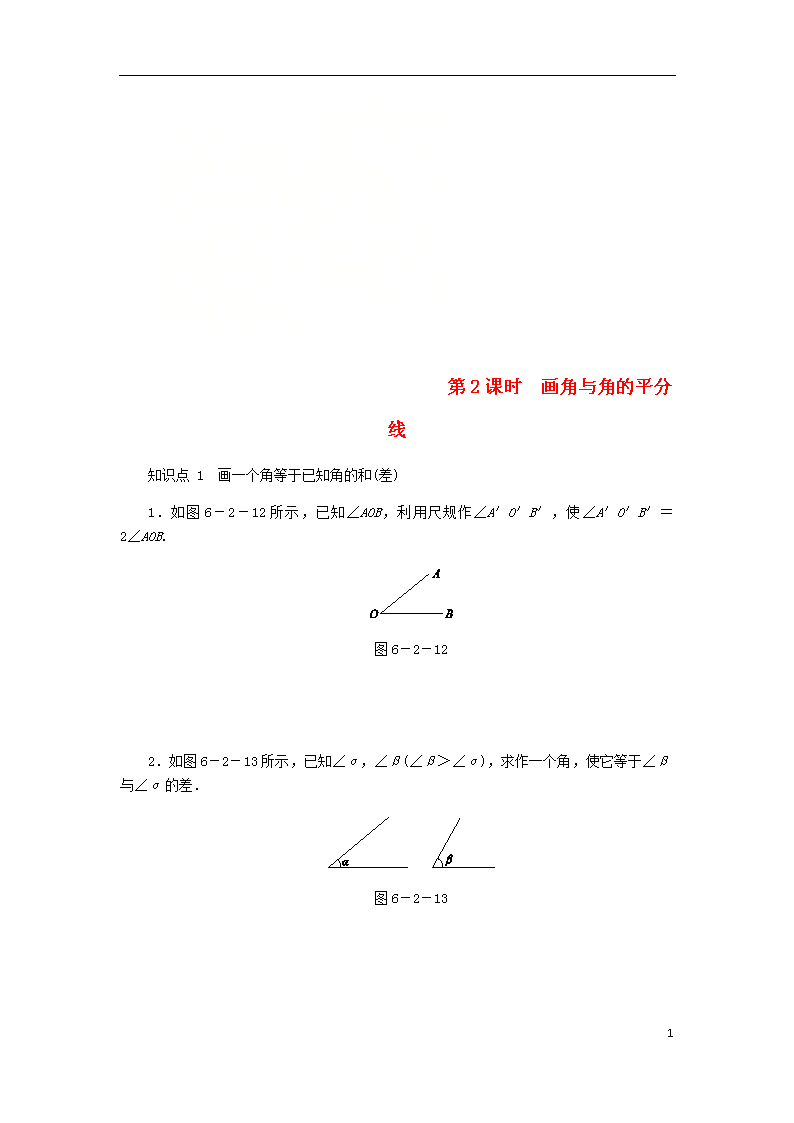
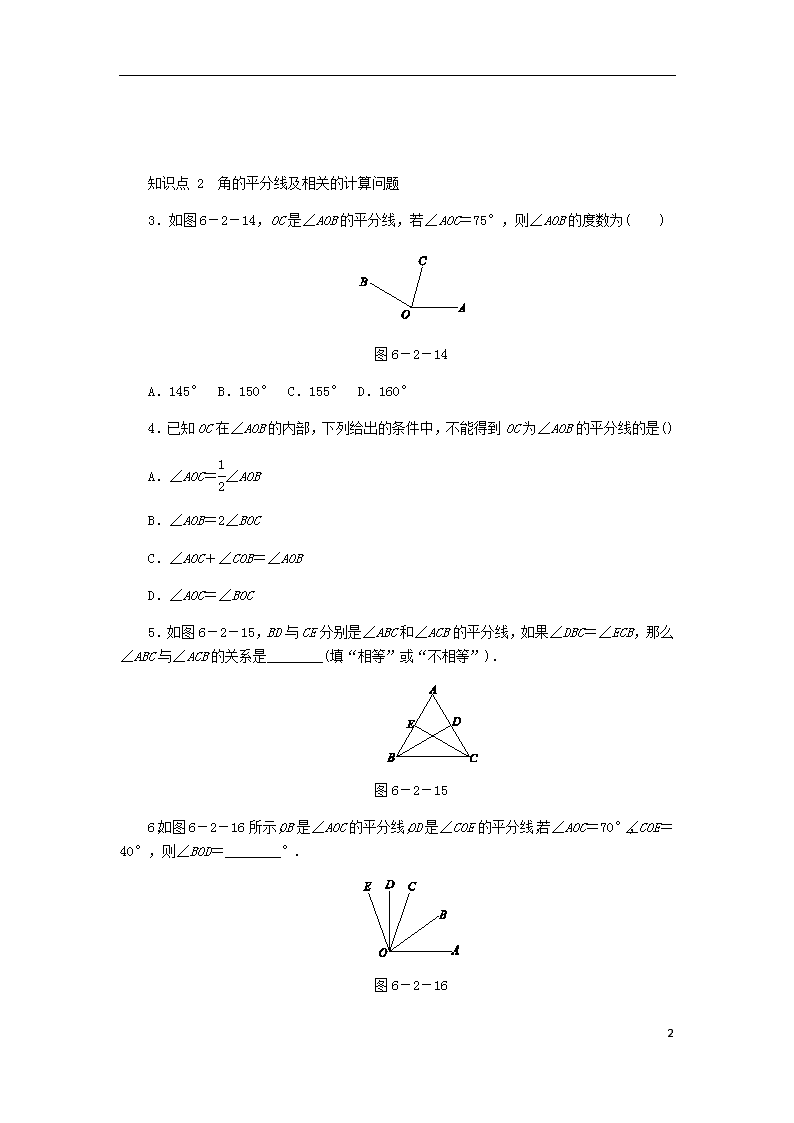
第2课时　画角与角的平分线 知识点 1　画一个角等于已知角的和(差)‎ ‎1．如图6－2－12所示，已知∠AOB，利用尺规作∠A′O′B′，使∠A′O′B′＝2∠AOB.‎ 图6－2－12‎ ‎2．如图6－2－13所示，已知∠α，∠β(∠β＞∠α)，求作一个角，使它等于∠β与∠α的差．‎ 图6－2－13‎ 10‎ 知识点 2　角的平分线及相关的计算问题 ‎3．如图6－2－14，OC是∠AOB的平分线，若∠AOC＝75°，则∠AOB的度数为(　　)‎ 图6－2－14‎ A．145° B．150° C．155° D．160°‎ ‎4．已知OC在∠AOB的内部，下列给出的条件中，不能得到OC为∠AOB的平分线的是()‎ A．∠AOC＝∠AOB B．∠AOB＝2∠BOC C．∠AOC＋∠COB＝∠AOB D．∠AOC＝∠BOC ‎5．如图6－2－15，BD与CE分别是∠ABC和∠ACB的平分线，如果∠DBC＝∠ECB，那么∠ABC与∠ACB的关系是________(填“相等”或“不相等”)．‎ ‎　　　‎ 图6－2－15‎ ‎6．如图6－2－16所示，OB是∠AOC的平分线，OD是∠COE的平分线，若∠AOC＝70°，∠COE＝40°，则∠BOD＝________°.‎ 图6－2－16‎ 10‎ ‎7．如图6－2－17，OC是∠AOB的平分线，OD是∠AOC的平分线，且∠COD＝25°10′，则∠AOB的度数为________．‎ 图6－2－17‎ ‎8. 如图6－2－18，O是直线AB上的一点，OD是∠COA的平分线，OE是∠BOC的平分线，则∠AOD＋∠BOE＝________°.‎ ‎　　‎ 图6－2－18‎ ‎9．如图6－2－19，已知∠1＝40°，OD平分∠BOC，求∠AOD的度数．‎ 图6－2－19‎ ‎10．如图6－2－20，OE为∠AOD的平分线，∠COD＝∠EOC，∠COD＝15°，求∠AOD的度数．‎ 10‎ 图6－2－20‎ ‎11．考点办公室设在校园中心点O处，带队老师休息室A位于点O处的北偏东45°，某考场B位于点O处南偏东60°，请在图6－2－21中画出射线OA，OB，并计算∠AOB的度数．‎ 图6－2－21‎ ‎ ‎ ‎12．如图6－2－22，OB，OC是∠AOD的三等分线，则下列等式中不正确的是(　　)‎ 10‎ 图6－2－22‎ A．∠AOD＝3∠BOC B．∠AOD＝2∠AOC C．∠AOB＝∠BOC D．∠COD＝∠AOC ‎13．下列各度数的角，不能通过拼摆一副三角尺直接画出的是(　　)‎ A．15° B．75° C．105° D．130°‎ ‎14．如图6－2－23，OC是∠AOD的平分线，OE是∠DOB的平分线．‎ ‎(1)如果∠AOB＝130°，那么∠COE的度数是多少？‎ ‎(2)在(1)的条件下，若∠COD＝20°，则∠BOE的度数是多少？‎ 图6－2－23‎ ‎15．已知：如图6－2－24，∠BOC＝2∠AOC，OD平分∠AOB，且∠AOB＝120°，求∠AOC和∠COD的度数．‎ 10‎ 图6－2－24‎ ‎16．如图6－2－25，BD平分∠ABC，BE分∠ABC为 2∶5两部分，∠DBE＝21°，求∠ABC的度数．‎ 图6－2－25‎ 10‎ ‎17．已知一条射线OA，若从点O处引两条射线OB和OC，使∠AOB＝60°，∠BOC＝20°，画出∠AOC的平分线OM，并求出∠AOM的度数．‎ 10‎ ‎1．解：作法：①作∠DO′B′＝∠AOB；‎ ‎②在∠DO′B′的外部作∠A′O′D＝∠AOB，∠A′O′B′就是所求的角．如图所示：‎ ‎2．解：如图，∠AOC就是所求的角．‎ ‎3．B　[解析] ∵OC是∠AOB的平分线，∠AOC＝75°，∴∠AOB＝2∠AOC＝150°.故选B.‎ ‎4．C ‎5．相等　[解析] 若∠DBC＝∠ECB，则这两个角的2倍也相等．‎ ‎6．55　[解析] ∵∠DOC＝×40°＝20°，∠BOC＝×70°＝35°，∴∠BOD＝∠DOC＋∠BOC＝20°＋35°＝55°.‎ ‎7．100°40′　[解析] ∵OD是∠AOC的平分线，‎ 且∠COD＝25°10′，∴∠AOC＝2×25°10′＝50°20′.‎ ‎∵OC是∠AOB的平分线，‎ ‎∴∠AOB＝50°20′×2＝100°40′.‎ ‎8．90　[解析] ∵∠AOB是平角，OD是∠COA的平分线，OE是∠BOC的平分线，‎ ‎∴∠AOD＋∠BOE＝×180°＝90°.‎ ‎9．解：∵∠1＝40°，∴∠BOC＝180°－40°＝140°.∵OD平分∠BOC，∴∠COD＝∠BOC＝‎ 10‎ ×140°＝70°，∴∠AOD＝∠1＋∠COD＝40°＋70°＝110°.‎ ‎10．解：∵∠COD＝∠EOC，∠COD＝15°，‎ ‎∴∠EOC＝4∠COD＝60°，‎ ‎∴∠EOD＝∠EOC－∠COD＝45°.‎ ‎∵OE为∠AOD的平分线，‎ ‎∴∠AOD＝2∠EOD＝90°.‎ ‎11．[解析] 根据方向角的相关知识，找出中心点，根据题意画出图形．‎ 解：如图所示，因为∠1＝45°，∠2＝60°，‎ 所以∠AOB＝180°－(45°＋60°)＝75°.‎ ‎12． B ‎13．D.‎ ‎14．解：(1)∵OC是∠AOD的平分线，OE是∠DOB的平分线，‎ ‎∴∠COD＝∠AOD，∠DOE＝∠DOB，‎ ‎∴∠COD＋∠DOE＝∠AOD＋∠DOB＝‎ (∠AOD＋∠DOB)＝∠AOB，‎ ‎∴∠COE＝∠AOB.‎ ‎∵∠AOB＝130°，∴∠COE＝65°.‎ ‎(2)∵∠COE＝65°，∠COD＝20°，‎ ‎∴∠DOE＝∠COE－∠COD＝65°－20°＝45°.‎ 10‎ ‎∵OE平分∠DOB，‎ ‎∴∠BOE＝∠DOE＝45°.‎ ‎15．解：设∠AOC＝x°，∵∠BOC＝2∠AOC，∴∠BOC＝2x°，∴∠AOB＝∠AOC＋∠BOC＝3x°＝120°，∴x＝40，∴∠AOC＝40°.∵OD平分∠AOB，∴∠AOD＝∠AOB＝60°，∴∠COD＝∠AOD－∠AOC＝20°.‎ ‎16．解：设∠ABE＝2x°，由题意得2x＋21＝5x－21，‎ 解得x＝14，则∠ABC＝14°×7＝98°.‎ 所以∠ABC的度数是98°.‎ ‎17．解：当OC在∠AOB的内部时，如图①.‎ 因为∠AOC＝∠AOB－∠BOC＝60°－20°＝40°，且OM平分∠AOC，所以∠AOM＝∠AOC＝×40°＝20°；‎ 当OC在∠AOB的外部时，如图②.‎ 因为∠AOC＝∠AOB＋∠BOC＝60°＋20°＝80°，且OM平分∠AOC，所以∠AOM＝∠AOC＝×80°＝40°.‎ 综上所述，∠AOM的度数为20°或40°.‎ 10‎