2019七年级数学下册 培优新帮手 专题06 有理数的计算试题 （新版）新人教版 11页

1 专题 06 有理数的计算 阅读与思考 在小学我们已经学会根据四则运算法则对整数和分数进行计算，当引进负数概念后，数集扩大 到了有理数范围，我们又学习了有理数的计算，有理数的计算与算术数的计算有很大的不同：首先， 有理数计算每一步要确定符号；其次，代数与算术不同的是“字母代数”，所以有理数的 计算很多 是字母运算，也就是通常说的符号演算． 　　数学竞赛中的计算通常与推理相结合，这不但要求我们能正确地算出结果，而且要善于观察问 题的结构特点，将推理与计算相结合，灵活选用算法和技巧，提高计算的速度．有理数的计算常用 的技巧与方法有： 1．利用运算律． 2．以符代数． 3．裂项相消． 4．分解相约． 5．巧用公式等． 例题与求解 【 例 1 】 已 知 m ， n 互 为 相 反 数 ， a ， b 互 为 负 倒 数 ， x 的 绝 对 值 等 于 3 ， 则 的值等于______________． （湖北省黄冈市竞赛试题） 解题思路：利用互为相反数、互为倒数的两个有理数的特征计算． 【例 2 】 已知整数 满足 ，且 ，那么 等于（ ） A． 0 B． 10 C．2 D．12 （江苏省竞赛试题） 解题思路：解题的关键是把 25 表 示成 4 个不同的整数的积的形式． 2002200123 )()()1(- abxnmxabnmx ++++++ dcba ,,, 25=abcd dcba >>> dcba +++ 2 【例 3】 计算： （1） （“祖冲之杯”邀请赛试题） （2） ； （江苏省泰州市奥校竞赛试题） （3） ． （“希望杯”邀请赛试题） 解题思路：对于（1），若先计算每个分母值，则掩盖问题的实质，不妨先从考察一般情形入手； 对于（2），由于相邻的后一项与前一项的比都是 7， 考虑用字母表示和式；（3）中裂项相消，简化 计算． 【例 4】 都是正整数，并且 ， ． (1)证明： ， ； (2)若 ，求 和 的值． （“华罗庚金杯”少年邀请赛试题） 解题思路：（1）对题中已知式子进行变形．（2）把（1）中证明得到的式子代入，再具体分析 求解． ;100321 1 321 1 21 11 +⋅⋅⋅++++⋅⋅⋅++++++ 1998432 77777 +⋅⋅⋅++++ 90 1972 71856 1742 41630 1520 19412 136 522 11 +−+−+−+− nm, )11)(11()3 11)(3 11)(2 11)(2 11( mmA +−⋅⋅⋅+−+−= )11)(11()3 11)(3 11)(2 11)(2 11( nnB +−⋅⋅⋅+−+−= m mA 2 1+= n nB 2 1+= 26 1=− BA m n 3 【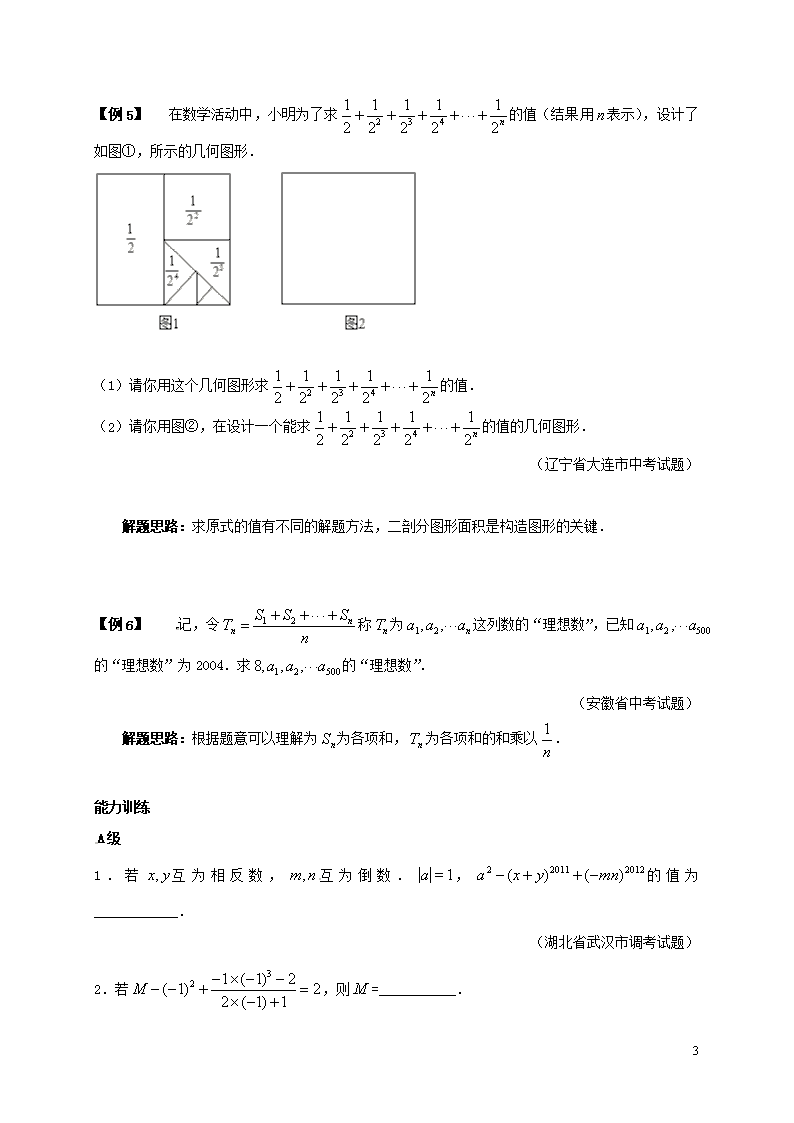例 5】 在数学活动中，小明为了求 的值（结果用 表示），设计了 如图①，所示的几何图形． （1）请你用这个几何图形求 的值． （2）请你用图②，在设计一个能求 的值的几何图形． （辽宁省大连市中考试题） 解题思路：求原式的值有不同的解题方法，二剖分图形面积是构造图形的关键． 【例 6】 记，令 称 为 这列数的“理想数”，已知 的“理想数”为 2004．求 的“理想数”． （安徽省中考试题） 解题思路：根据题意可以理解为 为各项和， 为各项和的和乘以 ． 能力训练 A 级 1 ． 若 互 为 相 反 数 ， 互 为 倒 数 ． ， 的 值 为 ____________． （湖北省武汉市调考试题） 2．若 ，则 =___________． n2 1 2 1 2 1 2 1 2 1 432 +⋅⋅⋅++++ n n2 1 2 1 2 1 2 1 2 1 432 +⋅⋅⋅++++ n2 1 2 1 2 1 2 1 2 1 432 +⋅⋅⋅++++ n SSST n n +⋅⋅⋅++= 21 nT naaa ⋅⋅⋅,, 21 50021 ,, aaa ⋅⋅⋅ 50021 ,,,8 aaa ⋅⋅⋅ nS nT n 1 yx, nm, 1=a 201220112 )()( mnyxa −++− 21)1(2 2)1(1)1( 3 2 =+−× −−×−+−−M M 4 （“希望杯”邀请赛试题） 3．计算：（1） ＝________________； （2） ＝__________________． 4．将 1997 减去它的 ，再减去余下的 ，再减去余下的 ，再减去余下的 ， ，依次类推， 直至最后减去余下的 ，最后的答案是_______________． （“祖冲之杯”邀请赛试题） 5．右图是一个由六个正方体组合而成的几何体，每个小正方体的六个面上都分别写着－1，2，3，－ 4，5，6 六个数字，那么图中所有看不见的面上的数字和是___________． （湖北省仙桃市中考试题） 6．如果有理数 满足关系式 ，那么代数式 的值（ ） A． 必为正数 B．必为负数 C．可正可负 D．可 能为 0 （江苏省竞赛试题） 7．已知有理数 两两不相等，则 ， ， 中负数的个数是（ ） A． 1 个 B． 2 个 C． 3 个 D．0 个或 2 个 （重庆市竞赛试题） 8．若 与 互为相反数，则 ＝（ ） A． 0 B． 1 C． －1 D．1997 （重庆市竞赛试题） 9．如果 ， ，则 的值是（ ） A．2 B． 1 C． 0 D．-1 19991997 1 97 1 75 1 53 1 ×+⋅⋅⋅+×+×+× ( ) ( ) ( ) ( )[ ]     −÷−÷−+−−×− 2 434 3 1622825.0 2 1 3 1 4 1 5 1 ⋅⋅⋅ 1997 1 cba ,, cba  0 32 - cab acbc zyx ,, zy x - y- x-z z-y y- - x xz a )-( b ab ba 1997 991898 22 + ( ) -12001 =+ba ( ) 1- 2002 =ba 20032003 ba + 5 （“希望杯”邀请赛试题） 10．若 是互为不相等的整 数，且 ，则 等于（ ） A．0 B． 4 C． 8 D．无法确定 11．把 ，3.7 ， ，2.9，4.6 分别填在图中五个Ο内，再在每个□中填上和它相连的三个Ο中 的数的平均数，再把三个□中的平均数填在△中．找出一种填法，使△中的数尽可能小，并求这个 数． （“华罗庚金杯”少年邀请赛试题） 12．已知 都不等于零，且 的最大值为 ，最小值为 ，求 的 值． B 级 1．计算： ＝________________． （“五羊杯”竞赛试题） 2．计算： ＝_________ _______． （“希望杯”邀请赛试题） 3．计算： ＝____________________． 4．据美国詹姆斯·马丁的测算，在近十年，人类的知识总量已达到每三年翻一翻，到 2020 年甚至 要达每 73 翻番空前速度，因此，基础教育任务已不是“教会一切人一切知识，而是让一切人学会学 习”． 已知 2000 年底，人类知识总量 ，假入从 2000 年底 2009 年底每 3 年翻一翻；从 2009 年底到 dcba ,,, 9=abcd dcba +++ 5 11 2 16 cba ,, abc abc c c b b a a +++ m n )1(1998 ++nm )98 97 98 3 98 1()6 5 6 3 6 1()4 3 4 1(2 1 +•••+++•••++++++ 1098765432 22-2-2-2-2-2-2-2-2 + 2)931862931 42842421( nnn nnn ••+•••+××+×× ••+•••+××+×× a 6 2019 年底每 1 年翻一番；2020 年是每 73 天翻一翻． （1）2009 年底人类知识总量是：__________________； （2）2019 年底人类知识总量是：_____ _____________； （3）2020 年按 365 天计算，2020 年底类知识总量会是_____________ _______． （北京市顺义区中考试题） 5．你能比较 和 的大小吗？ 为了解决这个问题，我们首先写出它的一般形式，即比较 与 的大小（n 是自然数）， 然后我们从分析 n=1，n=2，n=3…中发现规律，经归纳、猜想得出结论 （1）通过计算，比较下列各组中两数的大小：（在横线上填写“＞”“=”“＜”） ① ，② ；③ ；④ ；⑤ （ 2 ） 从 第 （ 1 ） 题 的 结 果 中 ， 经 过 归 纳 ， 可 以 猜 想 出 与 的 大 小 关 系 是 _____________________________________________________________________________； （3）根据以上归纳．猜想得到的一般结论，试比较下列两数的大小 _____ ：． （福建省龙岩市中考试题） 6．有 2009 个数排成一列，其中任意相邻的三个数中，中间的数总等于前后两数的和．若第一个数 是 1，第二个数是－1，则这个 2009 个数的和是（ ） A． －2 B．－1 C．0 D．2 （全国初中数学竞赛海南省试题） 7．如果 ，那么 的值为（ ） A． －1 B．1 C． D．不确定 （河北省竞赛试题） 8．三进位制数 201 可用十进制数表示为 ；二 进制数 1011 可用 20022001 20012002 1+nn nn )1( + 12 2__1 23 3__2 34 4__3 45 5__4 ••••••56 6__5 1+nn nn )1( + 20022001 20012002 1 3 3 2 2 1 1 =++ t t t t t t 321 321 ttt ttt 1± 19109213032 12 =++×=+×+× 7 十进制法表示为 ．前者按 3 的幂降幂排列，后者按 2 的 幂降幂排列，现有三进位制数 ，二进位制数 ，则 与 的大小关系为（ ）． A． B． C． D．不能确定 （重庆市竞赛试题） 9．如果有理数 满足 ，则（ ） A． B． C． D． （“希望杯”邀请赛试题） 10．有 1998 个互不相等的有理数，每 1997 个的和都是分母为 3998 的既约真分数，则这个 1998 个 有理数的和为（ ） A． B． C． D． （《学习报》公开赛试题） 11．观测下列各式： ， ， ．．． 回答下面的问题： （1）猜想 ＝______________．（直接写出你的结果） （2）利用你得到的（1）中的结论，计算 的值． （3）计算① 的值； ② 的值． 1112081212021 123 =+++=+×+×+× 221=a 10111=b a b ba > ba = ba < dcba ,,, dcba +>+ dcba +>++ 11- 2222 dcba +>+ 3333 dcba +>+ 4444 dcba +>+ 1997 999 1997 997 1998 998 1998 999 223 214 111 ××== 2233 324 1921 ××==+ 22333 434 136321 ××==++ 223333 544 11004321 ××==+++ 33333 )1-(321 nn ++•••+++ 33333 10099321 ++•••+++ 3333 100991211 ++•••++ 33333 10098642 ++•••+++ 8 9 专题 06 有理数的 计算 例1 28 或-26 例 2 D 提示 ：abcd=5×1×（-1）×（-5），a=-5，b=1，c=-1，d=-5. 例 3 （1） 提示： = = . （2） 提示：设 s= ，则 7s= （ 3 ） 原 式 = + =1+1- =2- = 例 4 （1）A= = = 同理 B= 由 A-B= - = = 得 ∴m= =13- ，又∵m，n 均为正整数，∴13+n 为 13×13 的因数，∴13+n= ∴n156，m=12. 例5 （1）原式=1- ，（2） 101 200 2 )1( 1 321 1 +−++++ nnn ( )1 2 +nn      +− 1 112 nn 6 771999 − 199832 7777 ++++  199932 7777 ++++       ++     +−+     ++     +−+     ++     +−+     + 56 1742 1730 1520 1512 136 132 11      ++     +− 90 1972 19 10 1 9 1 9 1 8 1 4 1 3 1 3 1 2 1 2 1 −+−++−+−+  10 1 10 91      +     +     +     −     −     − mm 113 112 11113 112 11  m m m m 1 3 4 2 31 3 2 2 1 +××××−×××  m m 2 1+ n n 2 1+ m m 2 1+ n n 2 1+ nm 2 1 2 1 − 26 1 13 111 =− nm n n +13 13 n+ × 13 1313 213 n2 1 10 例6 由 题 意 知 ， 即 . 又 ∴ =20 04×500. 故 8 ， ， ， … ， 的 “ 理 想 数 “ 为 ”” = =2008. A 级 1.2 提示：原式= =1+1=2. 2.2 提示：M-1+ ，解得 M=2. 3.（1） ；（2）-8 4. 1 提 示 ： 设 a=1997 ， 由 题 意 原 式 = = 5.-13 6.B 7.B 提示：不妨设 x>y>z. 8.B 9.D 10.A 11. 提 示 ： 设 ○ 内 从 右 到 左 填 的 数 分 别 为 ， ， ， ， 则 △ 内 填 的 数 为 . 要使△中填的数尽可能小，则 ， ， 分别为 2，9，3，7，而剩下的两个为 ， . ( ) ( ) ( )[ ]nn aaaaaaaaanT ++++++++++=  21321211 1 ( ) ( )[ ]nnn aaanannanT +++−+−+= −1321 2311  [ ]500499321500 2498499500500 1 aaaaaT +++++×=  500499321 2498499500 aaaaa +++++  1a 2a 500a [ ]500499321501 24984995008501501 1 aaaaaT ++++++×=  [ ]50020048501501 1 ×+×× ( )201220112 201 −+− 212 21 =+− − 5997 998 −     −−     −−− 4 1 623 1 22 aaaaaa 19961997342312 ×−−×−∗−×− aaaaa  1a 2a 3a 4a 5a 9 232 54321 aaaaa ++++ 5 113 =a 2a 4a 1a 5a 11 12.1998 提示 ： 时，m=4； 时，n-4. B 级 1.612.5 提示：倒叙相加. 2.6 提示： 3. 4.（1） （2） （3） 5.（1）略 （2）当 n<3 时， ；当 n≥3 时， （3）> 001-0007 6. A 提示：先写出前面一些数：1，－1，－2，－1，1，2，1，－1，…，经观察发现每 6 个数为一 次循环，又 2009＝334×6＋5.而每一组中 1＋（－1）＋（－2）＋（－1）＋1＋2＝0，故这 2009 个数的和，等于最后五个数之和.为 1＋（－1）＋（－2）＋（－1）＋1＝－2. 7. A 8. A 9. A 10 A 11.（1） ×π2×（n＋ 1）2 （2）原式＝ ×1002×（100＋1）2＝25 502 500 （3）①原式＝ ×100×（100＋1）2－ ×102×（10＋1）2＝25 499 475; ②原式＝23×（13＋23＋33＋…＋493＋503）＝23× ×502×（50＋1）2＝13 005 000. 1= x x 1−= x x nnn 222 1 =−+ 729 64 a•32 a•132 a•182 ( )nn nn 11 +<+ ( )nn nn 11 +>+ 1 4 1 4 1 4 1 4 1 4