人教版7年级下册数学全册教案第47课时 小结与复习 3页

1 第 47 课时 小结与复习 教学设计思想 本课是第八章的章节复习课，是学生再认知的过程，因此本课教 学时老师提出问题，引导学生独立完成，从过程中提高学生对问题的 进一步认识。首先让学生思考回答：① 二元一次方程组的解题思路 及基本方法。② 列一次方程组解应用题的步骤；然后师生共同讲评 训练题；最后小结。 教学目标 知识与技能 熟练地解二元一次方程组； 熟练地用二元一次方程组解决实际问题； 对本章的内容进行回顾和总结，进一步感受方程模型的重要性。 过程与方法 通过反思二元一次方程组应用于实际的过程（由实际问题中的数 量关系，经“逐步抽象”到建立方程组（实现数学化），由方程组的 解再到实际问题的答案），体会数学模型应用于实际的基本步骤。 情感态度价值观 通过反思消元法，进一步强化数学中的化归思想； 学会如何归纳知识，反思自己的学习过程。 教学方法： 复习法，练习法。 重、难点 重点：解二元一次方程组、列二元一次方程组解应用题。 难点：如何找等量关系，并把它们转化成方程。 解决办法：反复读题、审题，用简洁的语言概括出相等关系。 课时安排 1 课时。 教具准备 投影片 教学过程设计 2 （一）明确目标 前面已学过二元一次方程组及一次方程组的应用题，这一节课主 要把这一部分内容小结一下，并加以巩固练习。 （二）整体感知 本章含有两个主要思想：消元和方程思想。所谓方程思想是指在 求解数学问题时，从题中的已知量和未知量之间的数量关系人手，找 出相等关系，运用数学符号形成的语言将相等关系转化为方程（或方 程组），再通过解方程（组）使问题获得解决，方程思想是中学数学 中非常重要的数学思想方法之一，它的应用十分广泛。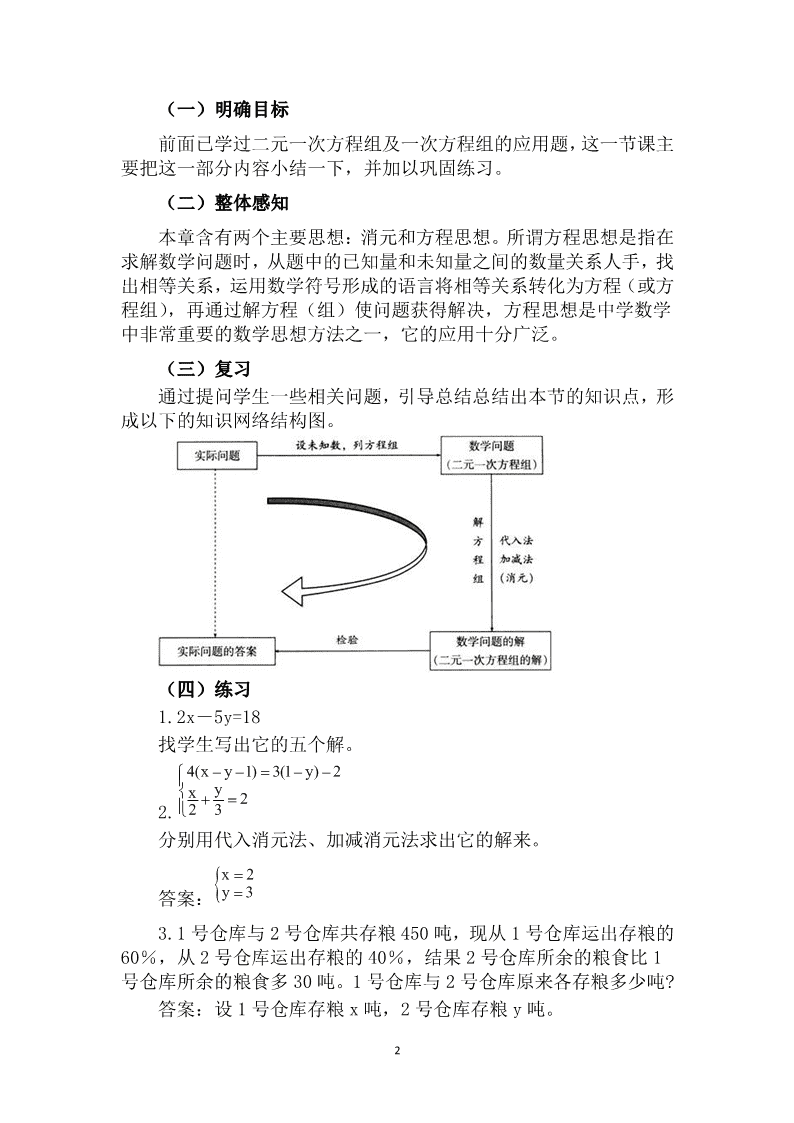 （三）复习 通过提问学生一些相关问题，引导总结总结出本节的知识点，形 成以下的知识网络结构图。 （四）练习 1.2x－5y=18 找学生写出它的五个解。 2. 4(x y 1) 3(1 y) 2 yx 223       分别用代入消元法、加减消元法求出它的解来。 答案：x2 y3   3.1 号仓库与 2 号仓库共存粮 450 吨，现从 1 号仓库运出存粮的 60％，从 2 号仓库运出存粮的 40％，结果 2 号仓库所余的粮食比 1 号仓库所余的粮食多 30 吨。1 号仓库与 2 号仓库原来各存粮多少吨? 答案：设 1 号仓库存粮 x 吨，2 号仓库存粮 y 吨。 3 x y 450 (1 0.6)x (1 0.4)y 30      解得 x 240 y 210   4.用 1 块 A 型钢板可制成 2 块 C 型钢板，1 块 D 型钢板；用 1 块 B 型钢板可制成 1 块 C 型钢板，2 块 D 型钢板。现需 15 块 C 型钢板， 18 块 D 型钢板，可恰好用 A 型钢板，B 型钢板各多少块? 答案：设用 x 块 A 型钢板，用 y 块 B 型钢板。 2x y 15 x 2y 18   解得 x4 y7   5.（我国古代问题）有大小两种盛酒的桶，已经知道 5 个大桶加 上 1 个小桶可以盛酒 3 斛（斛，音 hu 是古代的一种容量单位），1 个 大桶加上 5 个小桶可以盛酒 2 斛。1 个大桶、1 个小桶分别可以盛酒 多少斛？ 答案：设 1 个大桶可盛酒 x 斛、1 个小桶分别可以盛酒 y 斛。 5x y 3 x 5y 2   解得 13x 24 7y 24    （五）小结 引导学生总结本节的知识点。 （六）板书设计 小结与复习 知识结构图 练习