【北师大版】七年级下册数学第四章+三角形第1节《认识三角形》第三课时 10页

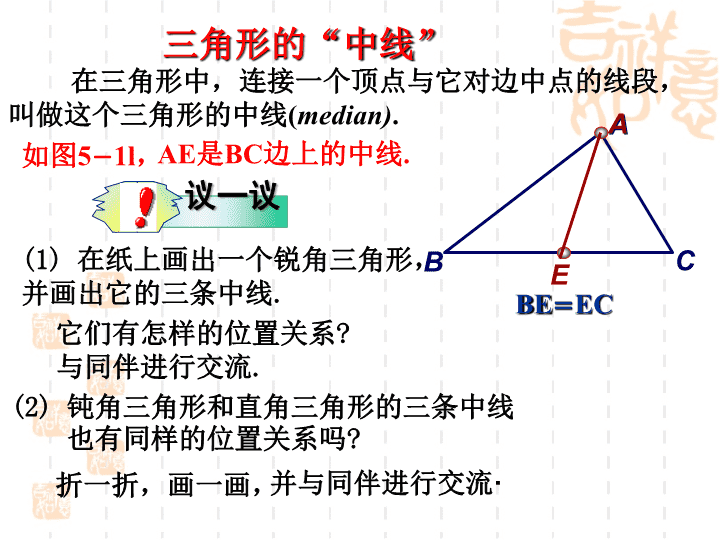
第四章 三角形 4.1.3 认识三角形 复习引入 什么叫线段的中点？ 2. 角平分线是怎样定义的？ 在三角形中，连接一个顶点与它对边中点的线段，叫做这个三角形的中线( median) . 三角形的“中线” BE = EC B A C E A 如图5 − 1l， AE是BC边上的中线. (1) 在纸上 画出一个锐角三角形， 并画出它的三条中线 . 议一议 它们有怎样的位置关系 ? 与同伴进行交流 . (2) 钝角三角形和直角三角形的三条中线 也有同样的位置关系吗 ? 折一折，画一画， 并与同伴进行交流 · 三角形的三条中线的性质 三角形的三条中线交于一点 . 议一议 在一张薄纸上任意画一个三角形，你能设法画出它的一个内角的平分线吗? B A C 注意 ! 用量角器画最简便。用圆规也能 你能通过折纸的方法得到它吗? 在一张纸上画出一个一个三角形并剪下，将它的一个角对折，使其两边重合。 折痕 AD 即为三角形的 ∠ A 的角平分线。 A B C A D 三形的角平分线的定义 以前所学的“角平分线”是一条射线， B A C “ 三角形的角平分线”还是射线 吗 ? 在三角形中，一个内角的平分线与它的对边相交，这个角的顶点与交点之间的 线段叫 三角形的角平分线。 “ 三角形的角平分线”是一条线段。 注意 ! D ∠1 = ∠2 1 2 三角形的角平分线的性质 每人准备锐角三角形、钝角三角形和直角三角形纸片各一个。 (1) 你能分别画出这三个三角形的三条角平分线吗? (2) 你能用折纸的办法得到它们吗? 做一做 (3) 在每个三角形中，这三条角平分线之间有怎样的 位置关系 ? 将你的结果与同伴进行交流 . 三角形的三条角平分线交于同一点 . 本 课 概 要 B D ∠1 = ∠2 1 2 A C BE = EC B A C E A 在三角形中，一个内角的平分线与它的对边相交， 这个角的顶点与交点之间的 线段叫三角形的角平分线。 三角形的三条中线交于一点 . 三角形的三条角平分线交于一点 . 在三角形中，连接一个顶点与它对边中点的线段，叫做 这个三角形的中线 ( median) . 补充例题 如图，在 △ ABC 中， BP 、 CP 分别是 ∠ B 、 ∠ C 的平分线，求证： ∠ BPC= 90˚ + ∠A 。 B A C P 证明： ∵ BP 、 CP 分别是 ∠ B 、 ∠ C 的平分线 ( 已知 ) ∴∠1= 1 ∠ABC ∠2= 2 ∠ ACB ∵ ∠BPC +∠1 + ∠2 = 180˚ ∠A +∠ABC +∠ACB= 180˚ ∴ ∠ BPC = 180˚ − ( ∠ 1 + ∠ 2 ) = 180˚ − ( + ) ∠ ABC ∠ ACB = 180˚ − (∠ ABC + ∠ ACB ) = 180˚ − ( 180˚ − ∠ A ) = 90˚ + ∠ A. 1. 今天你学到了什么？ 2. 你觉得角平分线有哪些注意点？ 3. 中线呢？ 4. 想一想在三角形中除了中线、 角平分线外还有其他线吗？ 小结