2019-2020学年陕西省渭南市韩城市七年级（下）期末数学试卷 解析版 17页

‎2019-2020学年陕西省渭南市韩城市七年级（下）期末数学试卷 一、选择题：本大题共10个小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．（3分）下列坐标中，在第三象限的是（　　）‎ A．（2，3） B．（2，﹣3） C．（﹣2，﹣3） D．（﹣2，3）‎ ‎2．（3分）如图，把河AB中的水引到C，拟修水渠中最短的是（　　）‎ A．CM B．CN C．CP D．CQ ‎3．（3分）计算：（+5）＝（　　）‎ A．5+ B．5+‎5‎ C．5+2 D．10‎ ‎4．（3分）下列调查中，比较适合用全面调查（普查）方式的是（　　）‎ A．了解某班同学立定跳远的情况 ‎ B．了解某种品牌奶粉中含三聚氰胺的百分比 ‎ C．了解一批炮弹的杀伤半径 ‎ D．了解全国青少年喜欢的电视节目 ‎5．（3分）如图，下列条件能判断AD∥BC的是（　　）‎ A．∠1＝∠4 B．∠1＝∠‎2 ‎C．∠2＝∠3 D．∠3＝∠4‎ ‎6．（3分）已知x＞y，则下列不等式成立的是（　　）‎ A．﹣2x＞﹣2y B．3x＞3y C．6﹣x＞6﹣y D．﹣‎ ‎7．（3分）若二元一次方程组的解为，则m﹣n的值是（　　）‎ A．1 B．‎2 ‎C．﹣ D．3‎ ‎8．（3分）小明要用40元钱买A、B两种型号的口罩，两种型号的口罩必须都买，40元钱全部用尽，A型每个6元，B型口罩每个4元，则小明的购买方案有（　　）种．‎ A．2种 B．3种 C．4种 D．5种 ‎9．（3分）已知关于x的不等式组的整数解只有三个，则a的取值范围是（　　）‎ A．a＞3或a＜2 B．2＜a＜ C．3＜a≤ D．3≤a＜‎ ‎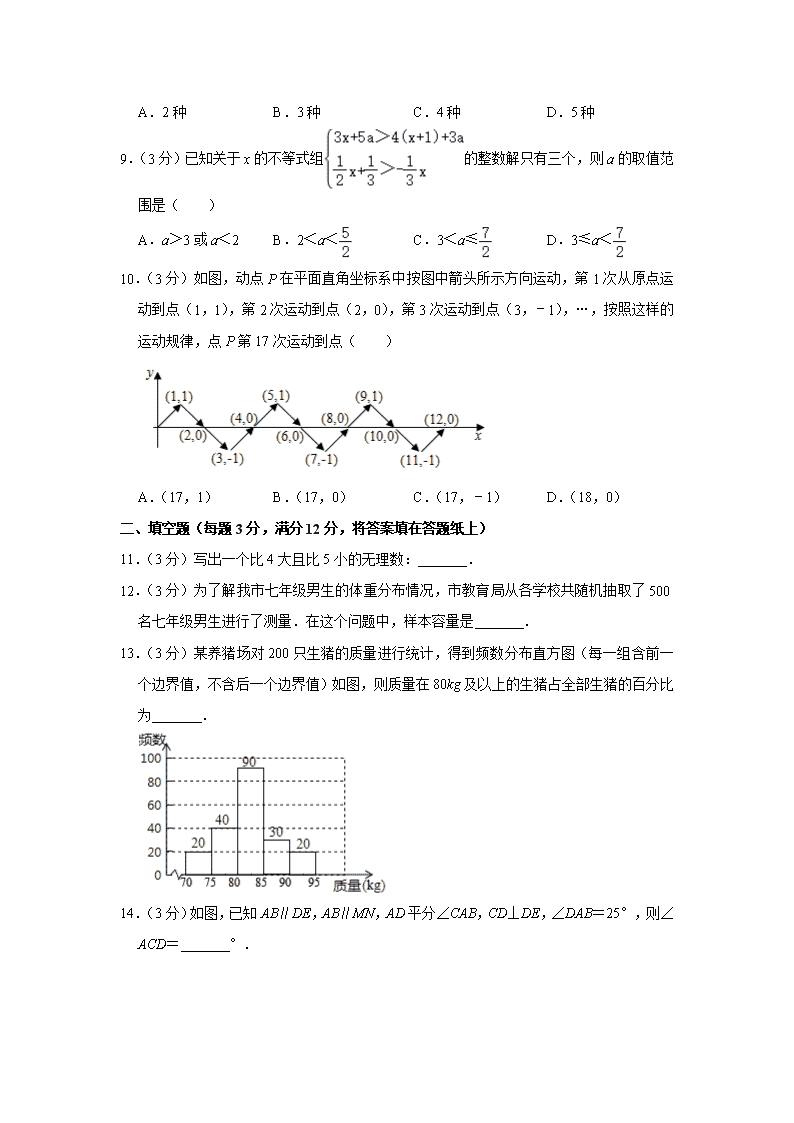10．（3分）如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次运动到点（2，0），第3次运动到点（3，﹣1），…，按照这样的运动规律，点P第17次运动到点（　　）‎ A．（17，1） B．（17，0） C．（17，﹣1） D．（18，0）‎ 二、填空题（每题3分，满分12分，将答案填在答题纸上）‎ ‎11．（3分）写出一个比4大且比5小的无理数：　 　．‎ ‎12．（3分）为了解我市七年级男生的体重分布情况，市教育局从各学校共随机抽取了500名七年级男生进行了测量．在这个问题中，样本容量是　 　．‎ ‎13．（3分）某养猪场对200只生猪的质量进行统计，得到频数分布直方图（每一组含前一个边界值，不含后一个边界值）如图，则质量在‎80kg及以上的生猪占全部生猪的百分比为　 　．‎ ‎14．（3分）如图，已知AB∥DE，AB∥MN，AD平分∠CAB，CD⊥DE，∠DAB＝25°，则∠ACD＝　 　°．‎ 三、解答题（共11小题，计78分．解答应写出过程）‎ ‎15．（3分）计算：+|﹣3|+．‎ ‎16．（3分）如图在平面直角坐标系中，已知点P（a，b）是三角形ABC内的任意一点，三角形ABC经过平移后得到三角形A1B‎1C1，点P的对应点为P1（a+6，b﹣2）．请在图中画出三角形A1B‎1C1．‎ ‎17．（8分）如图是某市区几个旅游景点的示意图（图中每个小正方形的边长为1个单位长度），若光岳楼的坐标为（﹣3，1），请建立平面直角坐标系，并用坐标表示动物园的位置．‎ ‎18．（8分）解不等式组并把它的解集表示在数轴上．‎ ‎19．（8分）已知‎5a+2的立方根是3，‎4a+2b﹣8的算术平方根是4，求a+3b的平方根．‎ ‎20．（8分）某商品进价是6000元，标价是9000元，需按标价打折出售，商店要求利润率不低于20%，至多可以打多少折？‎ ‎21．（8分）已知关于x，y的二元一次方程组的解x，y互为相反数，求a的值．‎ ‎22．（8分）如图，∠1+∠2＝180°，∠DEF＝∠A．试说明：ED∥AC．‎ ‎23．（8分）某校计划组织学生参加学校书法、摄影、篮球、乒乓球四个课外兴趣小组，要求每人必须参加并且只能选择其中的一个小组，为了解学生对四个课外小组的选择情况，学校从全体学生中随机抽取部分学生进行问卷调查，并把调查结果制成如图所示的两幅不完整的统计图．‎ ‎（1）求该校参加这次问卷调查的学生人数，并补全条形统计图；‎ ‎（2）求m，n的值；‎ ‎（3）求扇形统计图中“书法”所对应扇形的圆心角的度数．‎ ‎24．（8分）如图，AB∥DG，AD∥EF．‎ ‎（1）试说明：∠1+∠2＝180°；‎ ‎（2）若DG是∠ADC的平分线，∠2＝138°，求∠B的度数．‎ ‎25．（8分）我市某中学计划购进若干个排球和足球，如果购买20个排球和15个足球，一共需要花费2050元；如果购买10个排球和20个足球，一共需要花费1900元．‎ ‎（1）求每个排球和每个足球的价格分别是多少元？‎ ‎（2）如果学校要购买排球和足球共50个，并且预算总费用不超过3210元，那么该学校至多能购买多少个足球？‎ ‎2019-2020学年陕西省渭南市韩城市七年级（下）期末数学试卷 参考答案与试题解析 一、选择题：本大题共10个小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．（3分）下列坐标中，在第三象限的是（　　）‎ A．（2，3） B．（2，﹣3） C．（﹣2，﹣3） D．（﹣2，3）‎ ‎【分析】根据四个象限内点的坐标符号可得答案．‎ ‎【解答】解：A、（2，3）在第一象限，故此选项不合题意；‎ B、（2，﹣3）在第二象限，故此选项不合题意；‎ C、（﹣2，﹣3）在第三象限，故此选项符合题意；‎ D、（﹣2，3）在第四象限，故此选项不合题意；‎ 故选：C．‎ ‎2．（3分）如图，把河AB中的水引到C，拟修水渠中最短的是（　　）‎ A．CM B．CN C．CP D．CQ ‎【分析】根据点到直线的垂线段距离最短解答．‎ ‎【解答】解：如图，CP⊥AB，垂足为P，‎ 在P处开水渠，则水渠最短．‎ 因为直线外一点与直线上各点连线的所有线段中，垂线段最短．‎ 故选：C．‎ ‎3．（3分）计算：（+5）＝（　　）‎ A．5+ B．5+‎5‎ C．5+2 D．10‎ ‎【分析】根据乘法分配律可以解答本题．‎ ‎【解答】解：（+5）‎ ‎＝5+5，‎ 故选：B．‎ ‎4．（3分）下列调查中，比较适合用全面调查（普查）方式的是（　　）‎ A．了解某班同学立定跳远的情况 ‎ B．了解某种品牌奶粉中含三聚氰胺的百分比 ‎ C．了解一批炮弹的杀伤半径 ‎ D．了解全国青少年喜欢的电视节目 ‎【分析】由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似．‎ ‎【解答】解：A．了解某班同学立定跳远的情况，适合全面调查；‎ B．了解某种品牌奶粉中含三聚氰胺的百分比，适合抽样调查；‎ C．了解一批炮弹的杀伤半径，具有破坏性，适合抽样调查；‎ D．了解全国青少年喜欢的电视节目，适合抽样调查；‎ 故选：A．‎ ‎5．（3分）如图，下列条件能判断AD∥BC的是（　　）‎ A．∠1＝∠4 B．∠1＝∠‎2 ‎C．∠2＝∠3 D．∠3＝∠4‎ ‎【分析】根据平行线的判定解答即可．‎ ‎【解答】解：A、∵∠1＝∠4，∴AD∥BC，符合题意；‎ B、∵∠1＝∠2，不能判定AD∥BC，不符合题意；‎ C、∵∠2＝∠3，∴AB∥DC，不符合题意；‎ D、∵∠3＝∠4，不能判定AD∥BC，不符合题意；‎ 故选：A．‎ ‎6．（3分）已知x＞y，则下列不等式成立的是（　　）‎ A．﹣2x＞﹣2y B．3x＞3y C．6﹣x＞6﹣y D．﹣‎ ‎【分析】根据不等式的性质逐个判断即可．‎ ‎【解答】解：A、∵x＞y，‎ ‎∴﹣2x＜﹣2y，原变形不成立，故本选项不符合题意；‎ B、∵x＞y，‎ ‎∴3x＞3y，原变形成立，故本选项符合题意；‎ C、∵x＞y，‎ ‎∴6﹣x＜6﹣y，原变形不成立，故本选项不符合题意；‎ D、∵x＞y，‎ ‎∴﹣＜﹣，原变形不成立，故本选项不符合题意；‎ 故选：B．‎ ‎7．（3分）若二元一次方程组的解为，则m﹣n的值是（　　）‎ A．1 B．‎2 ‎C．﹣ D．3‎ ‎【分析】可解方程先求出x、y的值，再求m﹣n；亦可根据方程组系数特点，两式相加直接求解．‎ ‎【解答】解：‎ ‎①+②，得6x﹣6y＝12，‎ ‎∴x﹣y＝2．‎ 由于x＝m，y＝n，‎ ‎∴m﹣n＝2．‎ 故选：B．‎ ‎8．（3分）小明要用40元钱买A、B两种型号的口罩，两种型号的口罩必须都买，40元钱全部用尽，A型每个6元，B型口罩每个4元，则小明的购买方案有（　　）种．‎ A．2种 B．3种 C．4种 D．5种 ‎【分析】根据题意得出方程，进而得出方程的整数解解答即可．‎ ‎【解答】解：设A型x个，B型口罩y个，‎ 可得：6x+4y＝40，‎ 因为x，y取正整数，‎ 解得：，，，‎ 所以小明的购买方案有三种，‎ 故选：B．‎ ‎9．（3分）已知关于x的不等式组的整数解只有三个，则a 的取值范围是（　　）‎ A．a＞3或a＜2 B．2＜a＜ C．3＜a≤ D．3≤a＜‎ ‎【分析】先求出不等式组的解集，再根据不等式组的整数解只有三个，求出实数a的取值范围．‎ ‎【解答】解：解不等式3x+‎5a＞4（x+1）+‎3a，得：x＜‎2a﹣4，‎ 解不等式3x+‎5a+4＞4（x+1）+‎3a，得：x＞﹣，‎ ‎∵不等式组的整数解只有三个，‎ ‎∴这三个整数解为0、1、2，‎ ‎∴2＜‎2a﹣4≤3，‎ 解得3＜a≤，‎ 故选：C．‎ ‎10．（3分）如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次运动到点（2，0），第3次运动到点（3，﹣1），…，按照这样的运动规律，点P第17次运动到点（　　）‎ A．（17，1） B．（17，0） C．（17，﹣1） D．（18，0）‎ ‎【分析】令P点第n次运动到的点为Pn点（n为自然数）．列出部分Pn点的坐标，根据点的坐标变化找出规律“P4n（4n，0），P4n+1（4n+1，1），P4n+2（4n+2，0），P4n+3（4n+3，﹣1）”，根据该规律即可得出结论．‎ ‎【解答】解：令P点第n次运动到的点为Pn点（n为自然数）．‎ 观察，发现规律：P0（0，0），P1（1，1），P2（2，0），P3（3，﹣1），P4（4，0），P5（5，1），…，‎ ‎∴P4n（4n，0），P4n+1（4n+1，1），P4n+2（4n+2，0），P4n+3（4n+3，﹣1）．‎ ‎∵17＝4×4+1，‎ ‎∴P第17次运动到点（17，1）．‎ 故选：A．‎ 二、填空题（每题3分，满分12分，将答案填在答题纸上）‎ ‎11．（3分）写出一个比4大且比5小的无理数：　　．‎ ‎【分析】由于4＝，5＝，所以可写出一个二次根式，此根式的被开方数大于16且小于25即可．‎ ‎【解答】解：比4大且比5小的无理数可以是．‎ 故答案为．‎ ‎12．（3分）为了解我市七年级男生的体重分布情况，市教育局从各学校共随机抽取了500名七年级男生进行了测量．在这个问题中，样本容量是　500　．‎ ‎【分析】总体是指考查的对象的全体，个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体，而样本容量则是指样本中个体的数目．‎ ‎【解答】解：本题的样本是500名七年级男生的体重，故样本容量是500．‎ 故答案为：500．‎ ‎13．（3分）某养猪场对200只生猪的质量进行统计，得到频数分布直方图（每一组含前一个边界值，不含后一个边界值）如图，则质量在‎80kg及以上的生猪占全部生猪的百分比为　70%　．‎ ‎【分析】首先根据频数分布直方图确定质量在‎80kg及以上的生猪占全部生猪的频数，再计算百分比即可．‎ ‎【解答】解：质量在‎80kg及以上的生猪占全部生猪的频数：90+30+20＝140，‎ 百分比为×100%＝70%，‎ 故答案为：70%．‎ ‎14．（3分）如图，已知AB∥DE，AB∥MN，AD平分∠CAB，CD⊥DE，∠DAB＝25°，则∠ACD＝　40　°．‎ ‎【分析】依据角平分线的定义以及平行线的性质，即可得到∠ACM的度数，再根据垂线的定义，即可得到∠ACD的度数．‎ ‎【解答】解：∵AD平分∠CAB，‎ ‎∴∠BAC＝2∠DAB＝50°，‎ ‎∵AB∥MN，‎ ‎∴∠ACM＝∠BAC＝50°，‎ ‎∵AB∥DE，AB∥MN，‎ ‎∴MN∥DE，‎ 又∵CD⊥DE，‎ ‎∴CD⊥MN，‎ ‎∴∠ACD＝90°﹣∠ACM＝90°﹣50°＝40°，‎ 故答案为：40．‎ 三、解答题（共11小题，计78分．解答应写出过程）‎ ‎15．（3分）计算：+|﹣3|+．‎ ‎【分析】首先计算乘方、开方，然后从左向右依次计算，求出算式的值是多少即可．‎ ‎【解答】解：+|﹣3|+‎ ‎＝﹣3+3﹣+4‎ ‎＝4﹣．‎ ‎16．（3分）如图在平面直角坐标系中，已知点P（a，b）是三角形ABC内的任意一点，三角形ABC经过平移后得到三角形A1B‎1C1，点P的对应点为P1（a+6，b﹣2）．请在图中画出三角形A1B‎1C1．‎ ‎【分析】直接利用平移规律进而得出对应点位置进而得出答案．‎ ‎【解答】解：如图所示：△A1B‎1C1，即为所求．‎ ‎17．（8分）如图是某市区几个旅游景点的示意图（图中每个小正方形的边长为1个单位长度），若光岳楼的坐标为（﹣3，1），请建立平面直角坐标系，并用坐标表示动物园的位置．‎ ‎【分析】直接利用光岳楼的坐标为（﹣‎ ‎3，1），得出原点位置，进而得出动物园的坐标．‎ ‎【解答】解：如图所示：‎ 动物园（4，4）．‎ ‎18．（8分）解不等式组并把它的解集表示在数轴上．‎ ‎【分析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．‎ ‎【解答】解：，‎ 解不等式①，得：x≥﹣1，‎ 解不等式②，得：x＜3，‎ ‎∴不等式组的解集为﹣1≤x＜3，‎ 不等式组的解集在数轴上表示如下：‎ ‎19．（8分）已知‎5a+2的立方根是3，‎4a+2b﹣8的算术平方根是4，求a+3b的平方根．‎ ‎【分析】利用立方根的意义、算术平方根的意义，求出a、b的值，代入代数式求出值后，进一步求得平方根即可．‎ ‎【解答】解：∵‎5a+2的立方根是3，‎4a+2b﹣8的算术平方根是4，‎ ‎∴‎5a+2＝27，‎4a+2b﹣8＝16，‎ ‎∴a＝5，b＝2，‎ ‎∴a+3b＝5+6＝11，‎ ‎∴a+3b的平方根是±．‎ ‎20．（8分）某商品进价是6000元，标价是9000元，需按标价打折出售，商店要求利润率不低于20%，至多可以打多少折？‎ ‎【分析】设打x折销售，根据利润＝售价﹣进价结合利润率不低于20%，即可得出关于x的一元一次不等式，解之取其中的最大值即可得出结论．‎ ‎【解答】解：设打x折销售，‎ 依题意，得：9000×﹣6000≥6000×20%，‎ 解得：x≥8．‎ 答：至多可以打8折．‎ ‎21．（8分）已知关于x，y的二元一次方程组的解x，y互为相反数，求a的值．‎ ‎【分析】先求出方程组的解，根据相反数得出关于a的一元一次方程，求出方程的解即可．‎ ‎【解答】解：‎ ‎②﹣①，得3y＝﹣‎9a﹣3，‎ 即y＝﹣‎3a+1，‎ 把y＝﹣‎3a+1代入①得，x＝a﹣2，‎ 由题意得：a﹣2+（﹣‎3a+1）＝0，‎ 解得：a＝﹣0.5．‎ ‎22．（8分）如图，∠1+∠2＝180°，∠DEF＝∠A．试说明：ED∥AC．‎ ‎【分析】根据平行线的判定和性质解答即可．‎ ‎【解答】证明：因为∠1+∠DFE＝180°，∠1+∠2＝180°，‎ 所以∠DFE＝∠2，‎ 所以EF∥AB，‎ 所以∴∠DEF＝∠BDE，‎ 又因为∠DEF＝∠A，‎ 所以∠BDE＝∠A，‎ 所以DE∥AC．‎ ‎23．（8分）某校计划组织学生参加学校书法、摄影、篮球、乒乓球四个课外兴趣小组，要求每人必须参加并且只能选择其中的一个小组，为了解学生对四个课外小组的选择情况，学校从全体学生中随机抽取部分学生进行问卷调查，并把调查结果制成如图所示的两幅不完整的统计图．‎ ‎（1）求该校参加这次问卷调查的学生人数，并补全条形统计图；‎ ‎（2）求m，n的值；‎ ‎（3）求扇形统计图中“书法”所对应扇形的圆心角的度数．‎ ‎【分析】（1）根据选择书法的学生人数和所占的百分比，可以求得该校参加这次问卷调查的学生人数，然后根据扇形统计图中选择篮球的占28%，即可求得选择篮球的学生人数，从而可以将条形统计图补充完整；‎ ‎（2）根据条形统计图中的数据和（1）中的结果，可以得到m、n的值；‎ ‎（3）用360°乘以“书法”所占的百分比即可得出答案．‎ ‎【解答】解：（1）该校参加这次问卷调查的学生有：20÷20%＝100（人），‎ 篮球的人数有：100×28%＝28（人），‎ 补全的条形统计图如图所示：‎ ‎（2）m%＝×100%＝36%，即m＝36，‎ n%＝×100%＝16%，即n＝16；‎ ‎（3）“书法”所对应扇形的圆心角的度数为：360°×20%＝72°．‎ ‎24．（8分）如图，AB∥DG，AD∥EF．‎ ‎（1）试说明：∠1+∠2＝180°；‎ ‎（2）若DG是∠ADC的平分线，∠2＝138°，求∠B的度数．‎ ‎【分析】（1）直接利用平行线的性质得出∠BAD＝∠1，∠BAD+∠2＝180°，进而得出答案；‎ ‎（2）结合角平分线的定义以及平行线的性质得出答案．‎ ‎【解答】解：（1）∵AD∥EF，‎ ‎∴∠BAD+∠2＝180°，‎ ‎∵AB∥DG，‎ ‎∴∠BAD＝∠1，‎ ‎∴∠1+∠2＝180°．‎ ‎（2）∵∠1+∠2＝180°且∠2＝138°，‎ ‎∴∠1＝42°，‎ ‎∵DG是∠ADC的平分线，‎ ‎∴∠CDG＝∠1＝42°，‎ ‎∵AB∥DG，‎ ‎∴∠B＝∠CDG＝42°．‎ ‎25．（8分）我市某中学计划购进若干个排球和足球，如果购买20个排球和15个足球，一共需要花费2050元；如果购买10个排球和20个足球，一共需要花费1900元．‎ ‎（1）求每个排球和每个足球的价格分别是多少元？‎ ‎（2）如果学校要购买排球和足球共50个，并且预算总费用不超过3210元，那么该学校至多能购买多少个足球？‎ ‎【分析】（1）设每个排球的价格为x元，每个足球的价格为y元，根据“购买20个排球和15个足球，一共需要花费2050元；如果购买10个排球和20个足球，一共需要花费1900元”，即可得出关于x，y的二元一次方程组，解之即可得出结论；‎ ‎（2）设学校购买m个足球，则购买（50﹣m）个排球，根据预算总费用不超过3210元，即可得出关于m的一元一次不等式组，解之即可得出结论．‎ ‎【解答】解：（1）设每个排球的价格为x元，每个足球的价格为y元，‎ 依题意，得：．‎ 解得：．‎ 答：每个排球的价格为50元，每个足球的价格为70元；‎ ‎（2）设学校购买m个足球，则购买（50﹣m）个排球，‎ 依题意，得：50（50﹣m）+‎70m≤3210．‎ 解得：m≤．‎ 又∵m为整数，‎ ‎∴m的最大值为35．‎ 答：该学校至多能购买35个足球．‎