八年级数学上册第2章三角形2-1三角形第3课时三角形的内角和及外角课件 湘教版 19页

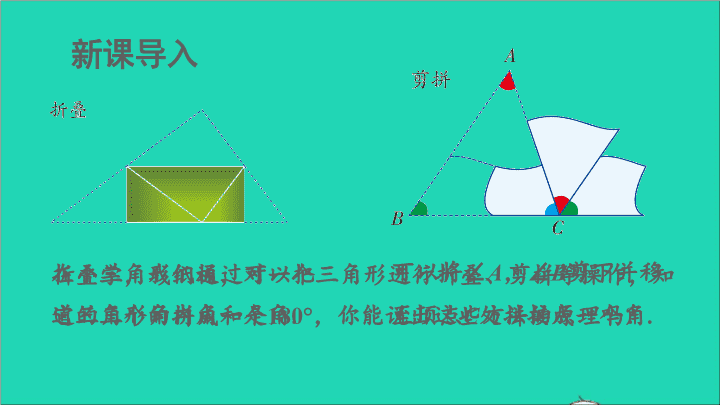
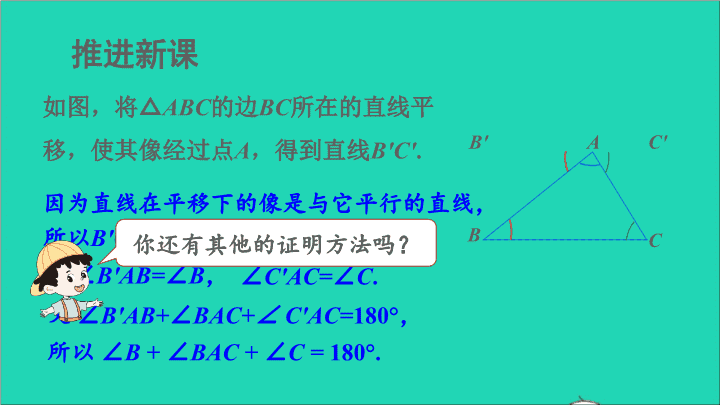
第3课时三角形的内角和及外角2 新课导入折叠三角形纸板，可以把它的三个角拼成一个角.可以将∠A，∠B剪下并移至顶点C处拼接成一个角.在小学，我们通过对一个三角形进行折叠、剪拼等操作，知道三角形的内角和是180°，你能说出这些方法的原理吗? 推进新课ABCB′C′如图，将△ABC的边BC所在的直线平移，使其像经过点A，得到直线B′C′.因为直线在平移下的像是与它平行的直线，所以B′C′//BC.则∠B′AB=∠B，∠C′AC=∠C.又∠B′AB+∠BAC+∠C′AC=180°，所以∠B+∠BAC+∠C=180°.你还有其他的证明方法吗？ ABCD如图，延长BC到D，E过C作CE∥BA，12所以∠A=∠1（两直线平行，内错角相等）∠B=∠2（两直线平行，同位角相等）又因为∠1+∠2+∠ACB=180°所以∠A+∠B+∠ACB=180° ABCE如图，过A作AE∥BC，所以∠B=∠BAE（两直线平行，内错角相等）∠EAB+∠BAC+∠C=180°（两直线平行，同旁内角互补）所以∠B+∠C+∠BAC=180° 三角形的内角和等于180°.为了证明三个角的和为180°，转化为一个平角或同旁内角互补，这种转化思想是数学中的常用方法. 在△ABC中，∠A的度数是∠B的度数的3倍，∠C比∠B大15°，求∠A，∠B，∠C的度数.解设∠B为x°，则∠A为(3x)°，∠C为(x+15)°，从而有3x+x+(x+15)=180.解得x=33.所以3x=99，x+15=48.答:∠A，∠B，∠C的度数分别为99°，33°，48°. 一个三角形的三个内角中，最多有几个直角？最多有几个钝角？三角形的内角和等于180°，因此最多有一个直角或一个钝角. 在三角形中：三个角都是锐角锐角三角形有一个角是直角直角三角形有一个角是钝角钝角三角形一个三角形中，最多有一个直角或钝角，最少有两个锐角，最多有三个锐角. 在直角三角形中，夹直角的两边叫作直角边，直角的对边叫作斜边.ABC直角三角形可用符号“Rt△”来表示，“Rt△ABC”直角边直角边斜边 试一试根据下列条件，判断△ABC的形状：（1）∠A=45°，∠B=65°；（2）∠C=110；（3）∠C=90°.∠C=75°锐角三角形∠C=110°＞90°钝角三角形∠C=90°直角三角形 ABCD如图，将△ABC的一边BC延长，得到∠ACD.像这样，三角形的一边与另一边的延长线所组成的角，叫作三角形的外角.外角相邻的内角对于外角∠ACD来说，∠ACB是与它相邻的内角，∠A，∠B是与它不相邻的内角.不相邻的内角 DABC我觉得可以利用“三角形的内角和等于180°”的结论去思考.如图，外角∠ACD和它不相邻的内角∠A，∠B之间有什么大小关系？ DABC如图，外角∠ACD和它不相邻的内角∠A，∠B之间有什么大小关系？因为∠ACD+∠ACB=180°,∠A+∠B+∠ACB=180°,所以∠ACD-∠A-∠B=0（等量减等量，差相等）.于是∠ACD=∠A+∠B. 三角形的一个外角等于与它不相邻的两个内角的和. 巩固练习1.填空:（1）在△ABC中，∠A=60°，∠B=∠C，则∠B=____；（2）在△ABC中，∠A-∠B=50°，∠C-∠B=40°，则∠B=____.60°30° 2.如图，AD是△ABC的角平分线，∠B=36°，∠C=76°，求∠DAC的度数.在△ABC中：∠BAC=180°－36°－76°=68°因为AD是△ABC的角平分线，所以∠DAC=68°÷2=34°. 3.如图，∠CAD=100°，∠B=30°，求∠C的度数.因为∠CAD是△ABC的外角，所以∠B+∠C=∠CAD，故∠C=100°－30°=70°. 课后小结你还有哪些收获？