2020八年级数学上册第2章特殊三角形2 6页

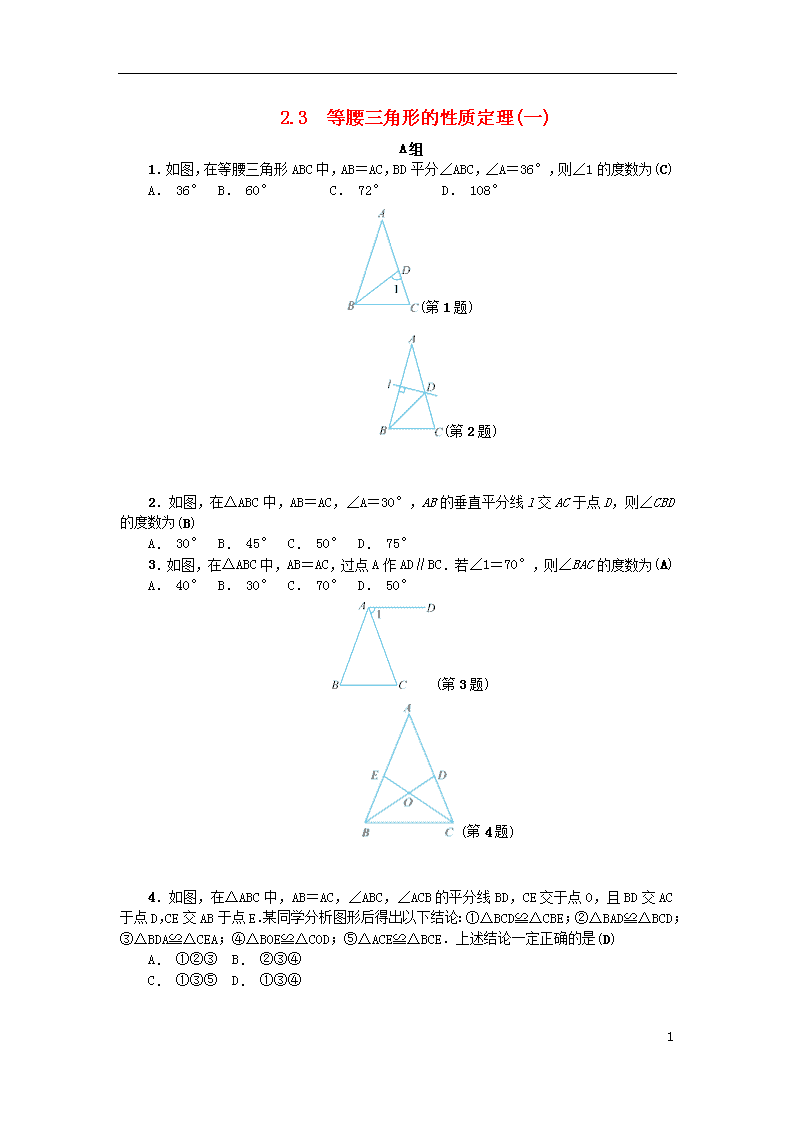
‎2.3 等腰三角形的性质定理(一)‎ A组 ‎1．如图，在等腰三角形ABC中，AB＝AC，BD平分∠ABC，∠A＝36°，则∠1的度数为(C)‎ A． 36° B． 60°　　　 C． 72°　　　 D． 108°‎ ‎(第1题)‎ ‎　　　　(第2题)‎ ‎2．如图，在△ABC中，AB＝AC，∠A＝30°，AB的垂直平分线l交AC于点D，则∠CBD的度数为(B)‎ A． 30° B． 45° C． 50° D． 75°‎ ‎3．如图，在△ABC中，AB＝AC，过点A作AD∥BC．若∠1＝70°，则∠BAC的度数为(A)‎ A． 40° B． 30° C． 70° D． 50°‎ ‎(第3题)‎ ‎　　　　 (第4题)‎ ‎4．如图，在△ABC中，AB＝AC，∠ABC，∠ACB的平分线BD，CE交于点O，且BD交AC于点D，CE交AB于点E．某同学分析图形后得出以下结论：①△BCD≌△CBE；②△BAD≌△BCD；③△BDA≌△CEA；④△BOE≌△COD；⑤△ACE≌△BCE．上述结论一定正确的是(D)‎ A． ①②③ B． ②③④‎ C． ①③⑤ D． ①③④‎ 6‎ ‎(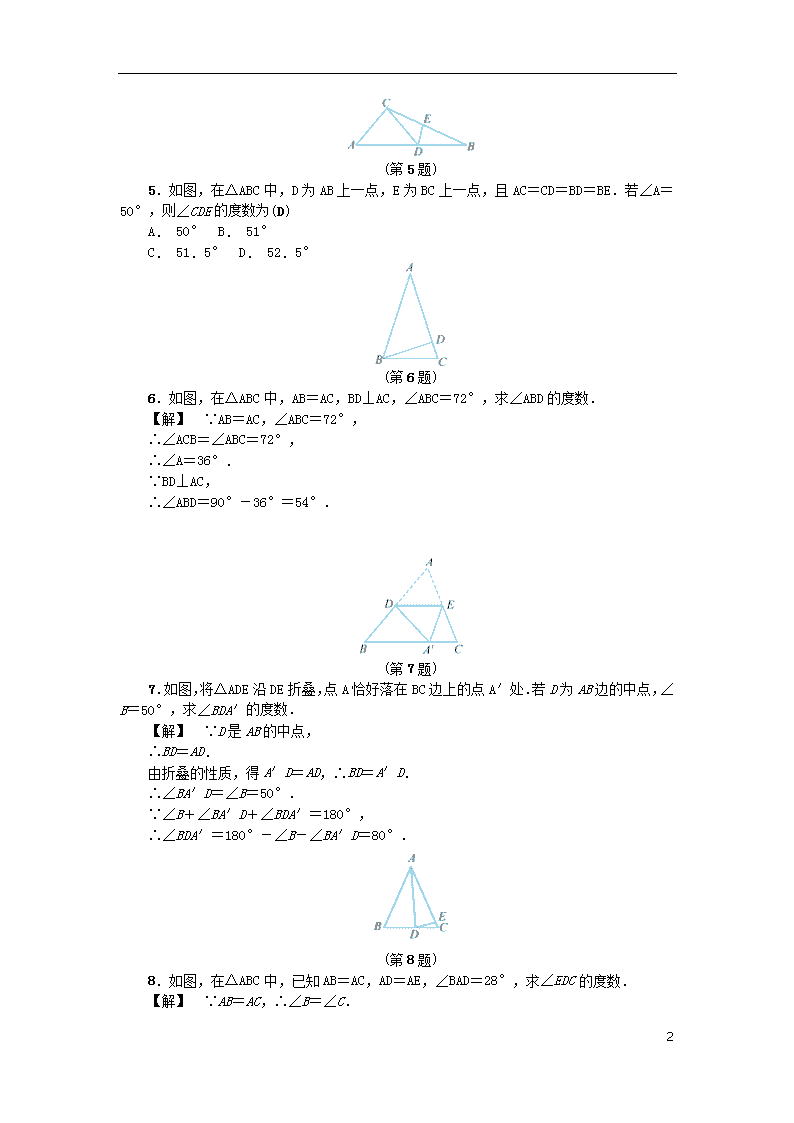第5题)‎ ‎5．如图，在△ABC中，D为AB上一点，E为BC上一点，且AC＝CD＝BD＝BE．若∠A＝50°，则∠CDE的度数为(D)‎ A． 50° B． 51°‎ C． 51．5° D． 52．5°‎ ‎(第6题)‎ ‎6．如图，在△ABC中，AB＝AC，BD⊥AC，∠ABC＝72°，求∠ABD的度数．‎ ‎【解】　∵AB＝AC，∠ABC＝72°，‎ ‎∴∠ACB＝∠ABC＝72°，‎ ‎∴∠A＝36°．‎ ‎∵BD⊥AC，‎ ‎∴∠ABD＝90°－36°＝54°．‎ ‎(第7题)‎ ‎7．如图，将△ADE沿DE折叠，点A恰好落在BC边上的点A′处．若D为AB边的中点，∠B＝50°，求∠BDA′的度数．‎ ‎【解】　∵D是AB的中点，‎ ‎∴BD＝AD．‎ 由折叠的性质，得A′D＝AD，∴BD＝A′D．‎ ‎∴∠BA′D＝∠B＝50°．‎ ‎∵∠B＋∠BA′D＋∠BDA′＝180°，‎ ‎∴∠BDA′＝180°－∠B－∠BA′D＝80°．‎ ‎(第8题)‎ ‎8．如图，在△ABC中，已知AB＝AC，AD＝AE，∠BAD＝28°，求∠EDC的度数．‎ ‎【解】　∵AB＝AC，∴∠B＝∠C．‎ 6‎ 同理，∠ADE＝∠AED．‎ 设∠EDC＝α，∠C＝β，‎ 则∠ADE＝∠AED＝∠EDC＋∠C＝α＋β，‎ ‎∠ADC＝∠ADE＋∠EDC＝α＋β＋α＝2α＋β．‎ ‎∵∠ADC＝∠BAD＋∠B＝28°＋β，‎ ‎∴2α＋β＝28°＋β，∴α＝14°，即∠EDC＝14°．‎ B组 ‎(第9题)‎ ‎9．如图，在△PAB中，PA＝PB，M，N，K分别是PA，PB，AB上的点，且AM＝BK，BN＝AK．若∠MKN＝44°，则∠P的度数为(D)‎ A． 44° B． 66° C． 88° D． 92°‎ ‎【解】　∵PA＝PB，∴∠A＝∠B．‎ 在△AMK和△BKN中，∵ ‎∴△AMK≌△BKN(SAS)．∴∠AMK＝∠BKN．‎ ‎∵∠MKB＝∠MKN＋∠BKN＝∠A＋∠AMK，‎ ‎∴∠A＝∠MKN＝44°，‎ ‎∴∠P＝180°－∠A－∠B＝92°．‎ ‎10．如图，已知AB＝A1B，A1B1＝A‎1A2，A2B2＝A‎2A3，A3B3＝A‎3A4，…．若∠A＝70°，则∠Bn－1AnAn－1的度数为(C)‎ ‎(第10题)‎ A． ° B． ° C． ° D． °‎ ‎【解】　在△ABA1中，∵∠A＝70°，AB＝A1B，‎ ‎∴∠BA‎1A＝∠A＝70°．‎ ‎∵A‎1A2＝A1B1，∠BA‎1A是△A‎1A2B1的外角，‎ ‎∴∠B‎1A2A1＝＝35°．‎ 同理，∠B‎2A3A2＝∠B‎1A2A1＝，∠B‎3A4A3＝∠B‎2A3A2＝，…，‎ 6‎ ‎∴∠Bn－1AnAn－1＝＝°．‎ ‎11．如图，在△ABC中，分别以AC，BC为边作等边三角形ACD和等边三角形BCE，连结AE，BD交于点O，求∠AOB的度数．‎ ‎ (第11题)‎ ‎【解】　设AC与BD交于点H．‎ ‎∵△ACD，△BCE都是等边三角形，‎ ‎∴CD＝CA，CB＝CE，∠ACD＝∠BCE＝60°，‎ ‎∴∠DCB＝∠ACE，‎ ‎∴△DCB≌△ACE(SAS)，‎ ‎∴∠CDB＝∠CAE．‎ 又∵∠DCH＋∠DHC＋∠CDB＝180°，‎ ‎∠AOH＋∠AHO＋∠CAE＝180°，‎ ‎∠DHC＝∠AHO，‎ ‎∴∠AOH＝∠DCH＝60°．‎ ‎∴∠AOB＝180°－∠AOH＝120°．‎ ‎12．如图，在△ABC中，AB＝AC，BD，CE是△ABC的两条高线，BD与CE相交于点O．‎ ‎(1)求证：OB＝OC．‎ ‎(2)若∠ABC＝70°，求∠BOC的度数．‎ ‎ (第12题)‎ ‎【解】　(1)∵AB＝AC，‎ ‎∴∠ABC＝∠ACB．‎ ‎∵BD，CE是△ABC的两条高线，‎ ‎∴∠BEC＝∠CDB＝90°．‎ 又∵BC＝CB，‎ ‎∴△BEC≌△CDB(AAS)，‎ ‎∴BE＝CD．‎ 又∵∠BOE＝∠COD，∠BEO＝∠CDO＝90°，‎ ‎∴△BOE≌△COD(AAS)，‎ ‎∴OB＝OC．‎ ‎(2)连结DE．‎ ‎∵∠ABC＝70°，AB＝AC，‎ ‎∴∠A＝180°－2×70°＝40°．‎ 6‎ ‎∵∠A＋∠AED＋∠ADE＝180°，∠OED＋∠ODE＋∠DOE＝180°，‎ ‎∴∠A＋∠AEO＋∠ADO＋∠DOE＝360°．‎ 又∵∠AEO＝∠ADO＝90°，‎ ‎∴∠A＋∠DOE＝180°，‎ ‎∴∠BOC＝∠DOE＝180°－40°＝140°．‎ ‎ (第13题)‎ ‎13．如图，在△ABC中，已知BC＝AC，∠BAC的外角平分线交BC的延长线于点D．若∠ADC＝∠CAD，求∠ABC的度数．‎ ‎ (第13题解)‎ ‎【解】　如解图，设∠ABC＝x，∠CAD＝y，‎ 则∠ACD＝2x，∠ADC＝∠CAD＝y，‎ ‎∴解得∴∠ABC＝36°．‎ 数学乐园 ‎14．(1)已知在△ABC中，∠A＝90°，∠B＝67．5°，请画一条直线，把这个三角形分割成两个等腰三角形(请你选用下面给出的备用图，把所有不同的分割方法都画出来．只需画图，不必说明理由，但要在图中标出相等两角的度数)．‎ ‎(2)已知在△ABC中，∠C是其最小的内角，过顶点B的一条直线把这个三角形分割成了两个等腰三角形，请探求∠ABC与∠C之间的关系．‎ ‎ (第14题)‎ 导学号：91354010‎ ‎【解】　(1)如解图①②(共有2种不同的分割法)．‎ ‎ (第14题解)‎ 6‎ ‎ (第14题解③)‎ ‎(2)设∠ABC＝y，∠C＝x，过点B的直线交边AC于点D．‎ 在△DBC中，‎ ‎①若∠C是顶角，如解图③，则∠CBD＝∠CDB＝90°－x，∠A＝180°－x－y．‎ 故∠ADB＝180°－∠CDB＝90°＋x＞90°，此时只能有∠A＝∠ABD，‎ 即180°－x－y＝y－，‎ ‎∴3x＋4y＝540°，∴∠ABC＝135°－∠C．‎ ‎②若∠C是底角，‎ 第一种情况：如解图④，当DB＝DC时，∠DBC＝x．在△ABD中，∠ADB＝2x，∠ABD＝y－x．‎ 若AB＝AD，则2x＝y－x，此时有y＝3x，‎ ‎∴∠ABC＝3∠C．‎ 若AB＝BD，则180°－x－y＝2x，此时有3x＋y＝180°，∴∠ABC＝180°－3∠C．‎ 若AD＝BD，则180°－x－y＝y－x，此时有y＝90°，即∠ABC＝90°，∠C为小于45°的任意锐角．‎ ‎, ④), ⑤)‎ ‎(第14题解)‎ 第二种情况：如解图⑤，当BD＝BC时，∠BDC＝x，∠ADB＝180°－x＞90°，此时只能有AD＝BD，∴∠A＝∠ABD＝∠BDC＝∠C＜∠C，这与题设∠C是最小角矛盾．‎ ‎∴当∠C是底角时，BD＝BC不成立．‎ 综上所述，∠ABC与∠C之间的关系是∠ABC＝135°－∠C或∠ABC＝3∠C或∠ABC＝180°－3∠C或∠ABC＝90°(∠C是小于45°的任意锐角)．‎ 6‎