等腰梯形的轴对称性（2）教案 2页

‎ ‎ ‎1．6 等腰梯形的轴对称性（2）‎ 教学目标：‎ ‎1、知道一个梯形是等腰梯形的判定条件； ‎ ‎2、能运用等腰梯形的性质和判定条件解决有关问题；‎ ‎3、在等腰梯形判定条件的探究过程中，进一步学习有条理地思考和表达，体会转化、类比等数学思想方法在解决问题中的作用。‎ 教学重点：等腰梯形判定 教学过程：‎ 一、创设情境：‎ 等腰梯形与等腰三角形有着紧密的联系.比照等腰三角形的特性，你对等腰梯形还有什么想法？试把你的想法写在下表的空格内：‎ ‎ ‎ ‎ 在△ABC中 如果AB＝AC，‎ 那么∠B＝∠C.‎ 如果∠B＝∠C，‎ 那么AB＝AC.‎ ‎ ‎ ‎ 在梯形ABCD中,‎ ‎ AD∥BC ‎⑴如果AB＝AC，‎ 那么∠B＝∠C；‎ ‎⑵如果AB＝AC，‎ 那么∠A＝∠D.‎ ‎？‎ 怎样说明你的猜想是正确的呢？‎ ‎（类比是发现新知、寻找规律、解决问题的一种重要方法.课本假设了等腰梯形与等腰三角形进行类比的情境，引导学生自然而然地提出“当梯形同一底上的两个角相等时，这个梯形会不会是等腰梯形呢”的猜想，同时萌生去探索这一想法是否正确的欲望）‎ 二、探索活动：‎ ‎1、探索思考：‎ 当梯形同一底上的两个角相等时，这个梯形会不会是等腰梯形呢？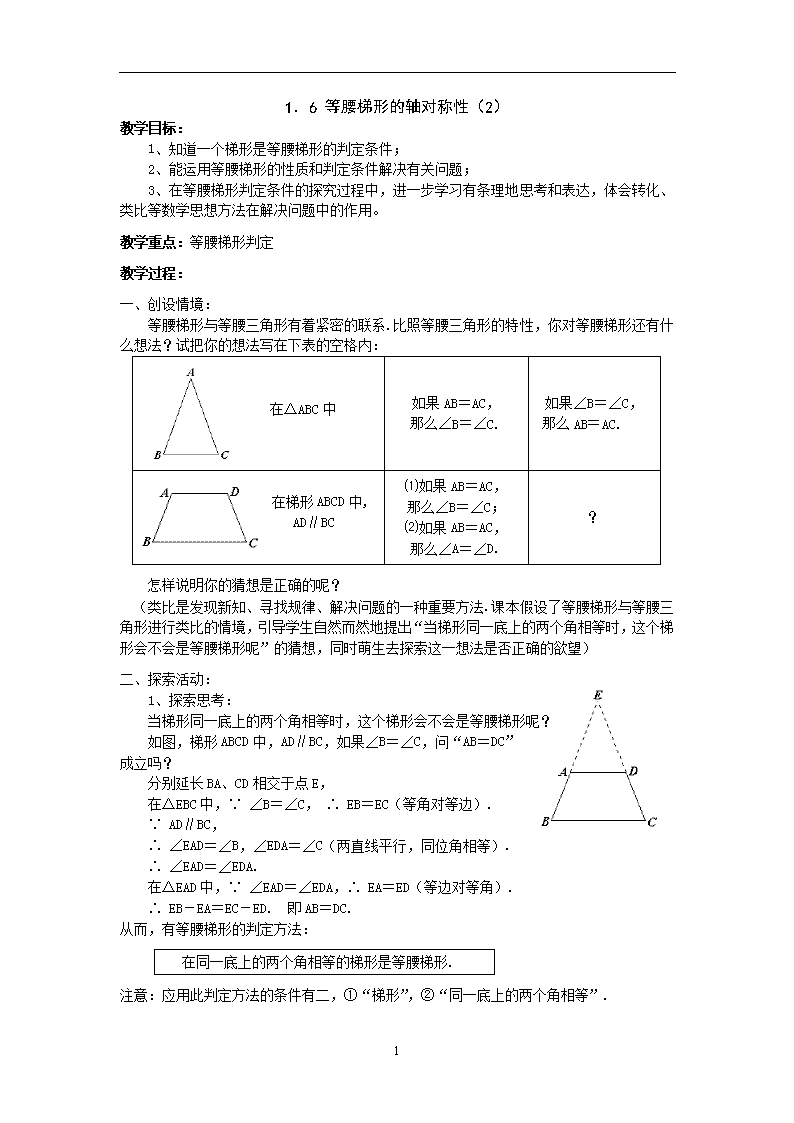‎ 如图，梯形ABCD中，AD∥BC，如果∠B＝∠C，问“AB＝DC”‎ 成立吗？‎ 分别延长BA、CD相交于点E，‎ 在△EBC中，∵ ∠B＝∠C， ∴ EB＝EC（等角对等边）.‎ ‎∵ AD∥BC， ‎ ‎∴ ∠EAD＝∠B，∠EDA＝∠C（两直线平行，同位角相等）.‎ ‎∴ ∠EAD＝∠EDA.‎ 在△EAD中，∵ ∠EAD＝∠EDA，∴ EA＝ED（等边对等角）.‎ ‎∴ EB－EA＝EC－ED. 即AB＝DC.‎ 从而，有等腰梯形的判定方法：‎ 在同一底上的两个角相等的梯形是等腰梯形.‎ 注意：应用此判定方法的条件有二，①“梯形”，②“同一底上的两个角相等”.‎ 2‎ ‎ ‎ ‎2、操作、验证：‎ 读句画图，验证猜想.‎ 如图，用三角尺在横格纸上画直线和直线， ‎ 能用图中字母表示的梯形（如梯形ABB1A1、‎ 梯形BD D1B1）是等腰梯形吗？为什么？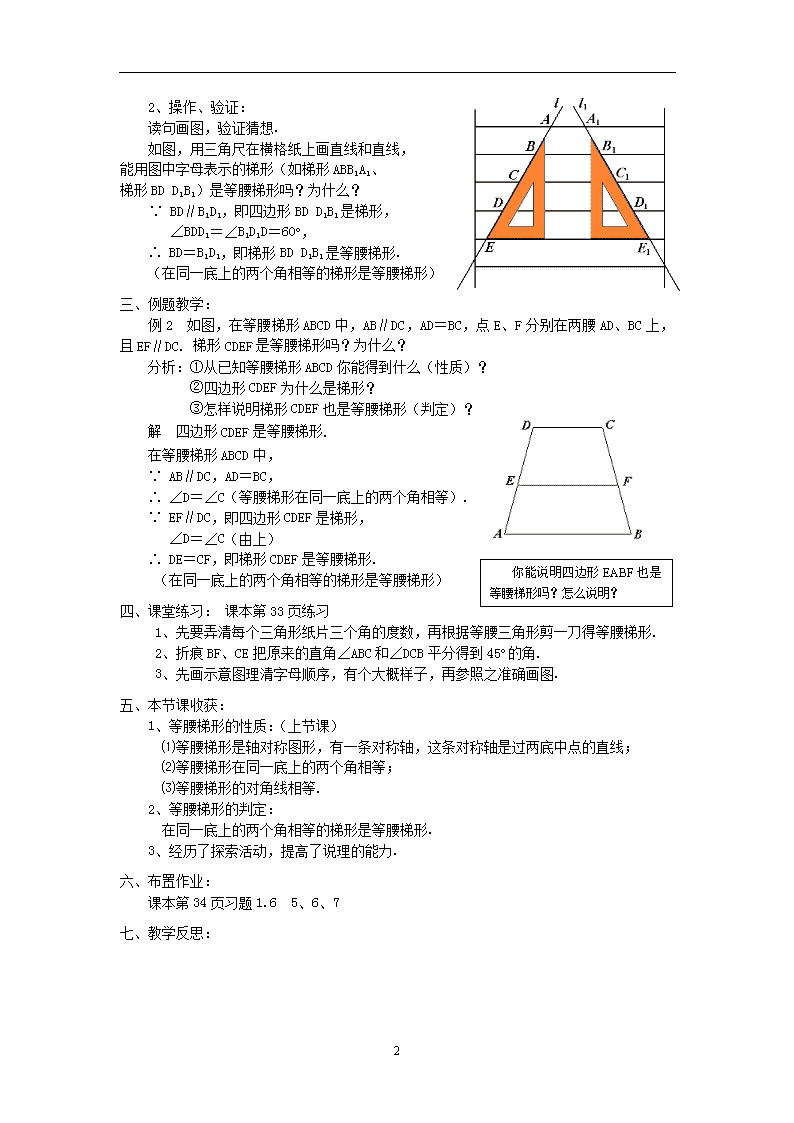 ‎ ‎∵ BD∥B1D1，即四边形BD D1B1是梯形，‎ ‎∠BDD1＝∠B1D1D＝60o，‎ ‎∴ BD＝B1D1，即梯形BD D1B1是等腰梯形.‎ ‎ （在同一底上的两个角相等的梯形是等腰梯形）‎ 三、例题教学：‎ 例2 如图，在等腰梯形ABCD中，AB∥DC，AD＝BC，点E、F分别在两腰AD、BC上，且EF∥DC. 梯形CDEF是等腰梯形吗？为什么？‎ 分析：①从已知等腰梯形ABCD你能得到什么（性质）？‎ ‎②四边形CDEF为什么是梯形？‎ ‎③怎样说明梯形CDEF也是等腰梯形（判定）？‎ 解 四边形CDEF是等腰梯形.‎ 在等腰梯形ABCD中，‎ ‎∵ AB∥DC，AD＝BC，‎ ‎∴ ∠D＝∠C（等腰梯形在同一底上的两个角相等）.‎ ‎∵ EF∥DC，即四边形CDEF是梯形，‎ ‎ ∠D＝∠C（由上）‎ 你能说明四边形EABF也是等腰梯形吗？怎么说明？‎ ‎∴ DE＝CF，即梯形CDEF是等腰梯形.‎ ‎（在同一底上的两个角相等的梯形是等腰梯形）‎ 四、课堂练习： 课本第33页练习 ‎ 1、先要弄清每个三角形纸片三个角的度数，再根据等腰三角形剪一刀得等腰梯形.‎ ‎2、折痕BF、CE把原来的直角∠ABC和∠DCB平分得到45o的角. ‎ ‎3、先画示意图理清字母顺序，有个大概样子，再参照之准确画图.‎ 五、本节课收获：‎ ‎1、等腰梯形的性质：（上节课）‎ ‎ ⑴等腰梯形是轴对称图形，有一条对称轴，这条对称轴是过两底中点的直线；‎ ‎⑵等腰梯形在同一底上的两个角相等；‎ ‎⑶等腰梯形的对角线相等.‎ ‎2、等腰梯形的判定：‎ 在同一底上的两个角相等的梯形是等腰梯形.‎ ‎3、经历了探索活动，提高了说理的能力.‎ 六、布置作业：‎ ‎ 课本第34页习题1.6 5、6、7‎ 七、教学反思：‎ 2‎