人教版八年级上册数学同步练习课件-第11章-11三角形的外角(第二课时) 15页

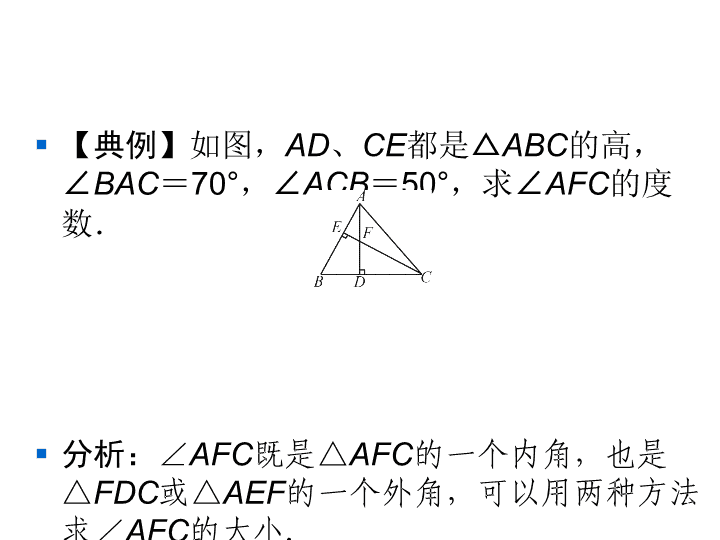
第十一章　三角形 11.2　与三角形有关的角 11.2.2　三角形的外角(第二课时) § 知识点1　三角形外角的概念 § 三角形的一边与另一边的延长线组成的角叫 做三角形的外角．如图，∠ACD就是△ABC 的一个外角． § 知识点2　三角形外角的性质 § 三角形的外角等于与它不相邻的两个内角的 和． § 注意：由三角形外角的性质还可以得出“三 角形的一个外角大于与它不相邻的任何一个 内角”的性质． 2 § 【典例】如图，AD、CE都是△ABC的高， ∠BAC＝70°，∠ACB＝50°，求∠AFC的 度数． § 分析：∠AFC既是△AFC的一个内角，也是 △FDC或△AEF的一个外角，可以用两种方 法求∠AFC的大小． 3 § 解答：(方法一)∵AD、CE是△ABC的高， ∴∠ADC＝∠AEC＝90°.∵∠BAC＝70°， ∠ACB＝50°，∴在△ADC中，∠DAC＝ 180°－90°－50°＝40°，在△AEC中， ∠ACE＝180°－70°－90°＝20°.∴在 △AFC中，∠AFC＝180°－20°－40°＝ 120°. § (方法二)在△ABC中，∵∠BAC＝70°， ∠ACB＝50°，∴∠B＝180°－70°－ 50°＝60°.∵AD、CE是△ABC的高， ∴∠BEC＝∠ADC＝90°，∴∠BCE＝ 180°－90°－60°＝30°，∴∠AFC＝ ∠ADC＋∠BCE＝90°＋30°＝120°. 4 § 1．【浙江衢州中考】如图，直线AB∥CD， ∠A＝70°，∠C＝40°，则∠E等于(　　) § A．30°　　 § B．40°　　 § C．60°　　 § D．70° 5 A 　 § 2．如图，已知AB∥CD，则(　　) § A．∠1＝∠2＋∠3　　 § B．∠1＝2∠2＋∠3 § C．∠1＝2∠2－∠3　　 § D．∠1＝180°－∠2－∠3 § 3．如图，CE是△ABC的外角∠ACD的平分 线，若∠B＝35°，∠ACE＝60°，则∠A ＝(　　) § A．35°　　 § B．95°　　 § C．85°　　 § D．75° 6 A 　 C 　 § 4．如图，平面上直线a、b分别过线段OK两 端点(数据如图)，则a、b相交所成的锐角为 __________度． § 解析：由三角形外角的性质可知，a、b相交 所成锐角为100°－70°＝30°. § 5．如图，a∥b，∠1＋∠2＝75°，则∠3＋ ∠4＝____________. 7 30　 105°　 § 6．如图，∠ABC＝38°， ∠ACB＝100°，AD平分∠BAC， AE是△ABC中BC边上的高，求 ∠DAE的度数． 8 § 7．一个零件的形状如图所示，按规 定∠A＝ 90°，∠B和∠C应分别是 32°和21°，检验工人量得∠BDC ＝ 148°，就断定这个零件不合格， 运用三角形外角的有关知识说明零 件不合格的理由． § 解：延长CD交AB于点E.∵∠A＝ 90°，∠C＝21°，∴∠DEB＝ ∠A＋∠C＝90°＋21°＝ 111°.∵∠B＝32°，∴∠CDB＝ ∠DEB＋∠B＝111°＋32°＝ 143°.∵已知∠CDB＝148°，∴ 该零件不合格． 9 § 8．如图，△ABC的三个顶点分别在直线a、 b上，且a∥b.若∠1＝120°，∠2＝80°， 则∠3的度数是(　　) § A．40°　　 § B．60°　　 § C．80°　　 § D．120° 10 A 　 § 9．如图所示，∠A、∠1、∠2的大小关系是 (　　) § A．∠A＞∠1＞∠2　　 § B．∠2＞∠1＞∠A § C．∠A＞∠2＞∠1　　 § D．∠2＞∠A＞∠1 § 10．如图，CE是△ABC的外角∠ACD的平 分线，交BA延长线于点E，若∠BAC＝ 100°，∠B＝42°，则∠E的度数为(　　) § A．27°　　 § B．28°　　 § C．29°　　 § D．30° 11 B 　 C 　 § 11．如图，△ABC中，∠C＝ 104°，BF平分∠ABC，且与 △ABC的外角平分线AE所在的直 线交于点F，则∠F＝ ___________. § 12．如图，已知∠A＝50°，∠B ＝60°，∠C＝40°，则∠ADC ＝____________. § 13．如图，∠A＋∠B＋∠C＋ ∠D＋∠E的度数为___________ 度． 12 52°　 150°　 180　 § 14．【2018·湖北宜昌中考】如图，在 Rt△ABC中，∠ACB＝90°，∠A＝40°， △ABC的外角∠CBD的平分线BE交AC的延 长线于点E. § (1)求∠CBE的度数； § (2)过点D作DF∥BE，交AC的延长线于点F， 求∠F的度数． 13 § 15．如图，CE是△ABC的一个外角∠ACD 的平分线，且EF∥BC交AB于点F，∠A＝ 60°，∠CEF＝50°，求∠B的度数． § 解：∵EF∥BC，∴∠ECD＝∠CEF＝50°. § ∵CE平分∠ACD，∴∠ACE＝∠ECD＝ 50°， § ∴∠ACD＝∠ACE＋∠ECD＝100°. § ∵∠A＝60°，∴∠B＝∠ACD－∠A＝ 100°－60°＝40°. 14 § 16．如图所示，已知∠A＝10°， ∠ABC＝90°，∠ACB＝∠DCE， ∠ADC＝∠EDF，∠CED＝ ∠FEG.求∠F的度数． 15 解：∵∠A＝10°，∠ABC＝90°，∴∠ACB＝180°－∠A－∠ABC＝80°. ∵∠ACB＝∠DCE，∴∠DCE＝∠ACB＝80°，∴∠BCD＝180°－∠ACB －∠DCE＝180°－80°－80°＝20° .∵∠ABC＝90°，∴∠CBD＝90°， ∴∠ADC＝180°－∠CBD－∠BCD＝180°－90°－20°＝70°.∵∠ADC＝ ∠EDF，∴∠EDF＝70°，∴∠CDE＝180°－∠ADC－∠EDF＝180°－70°－ 70°＝40°，∴∠DEC＝180°－∠CDE－∠DCE＝180°－40°－80°＝ 60°.∵∠CED＝∠FEG，∴∠FEG＝60°.∵∠FEG是△AEF的外角，∴∠F＝ ∠FEG－∠A＝60°－10°＝50°.