北师大版八年级数学下册单元检测题全套及答案（含期中期末检测题） 44页

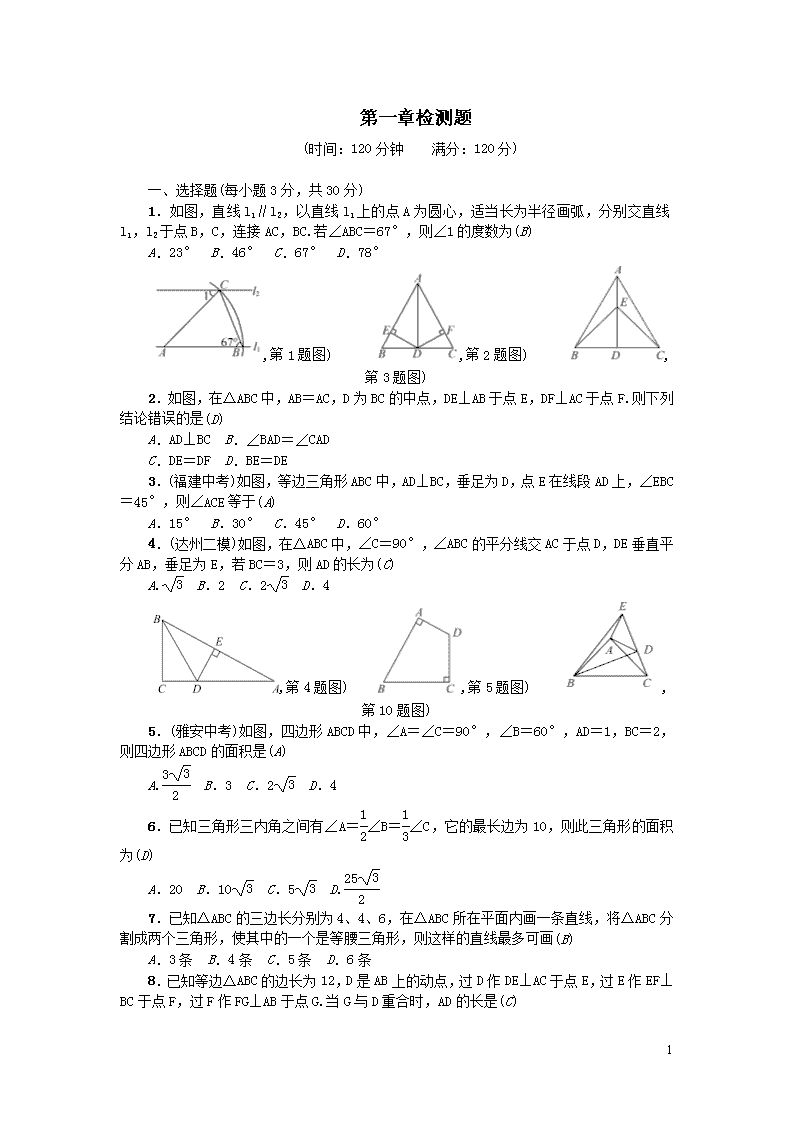
1 第一章检测题 (时间：120 分钟 满分：120 分) 一、选择题(每小题 3 分，共 30 分) 1．如图，直线 l1∥l2，以直线 l1 上的点 A 为圆心，适当长为半径画弧，分别交直线 l1， l2 于点 B，C，连接 AC，BC.若∠ABC＝67°，则∠1 的度数为(B) A．23° B．46° C．67° D．78° ,第 1 题图) ,第 2 题图) , 第 3 题图) 2．如图，在△ABC 中，AB＝AC，D 为 BC 的中点，DE⊥AB 于点 E，DF⊥AC 于点 F.则下列 结论错误的是(D) A．AD⊥BC B．∠BAD＝∠CAD C．DE＝DF D．BE＝DE 3．(福建中考)如图，等边三角形 ABC 中，AD⊥BC，垂足为 D，点 E 在线段 AD 上，∠EBC ＝45°，则∠ACE 等于(A) A．15° B．30° C．45° D．60° 4．(达州二模)如图，在△ABC 中，∠C＝90°，∠ABC 的平分线交 AC 于点 D，DE 垂直平 分 AB，垂足为 E，若 BC＝3，则 AD 的长为(C) A. 3 B．2 C．2 3 D．4 ,第 4 题图) ,第 5 题图) , 第 10 题图) 5．(雅安中考)如图，四边形 ABCD 中，∠A＝∠C＝90°，∠B＝60°，AD＝1，BC＝2， 则四边形 ABCD 的面积是(A) A.3 3 2 B．3 C．2 3 D．4 6．已知三角形三内角之间有∠A＝1 2 ∠B＝1 3 ∠C，它的最长边为 10，则此三角形的面积 为(D) A．20 B．10 3 C．5 3 D.25 3 2 7．已知△ABC 的三边长分别为 4、4、6，在△ABC 所在平面内画一条直线，将△ABC 分 割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画(B) A．3 条 B．4 条 C．5 条 D．6 条 8．已知等边△ABC 的边长为 12，D 是 AB 上的动点，过 D 作 DE⊥AC 于点 E，过 E 作 EF ⊥BC 于点 F，过 F 作 FG⊥AB 于点 G.当 G 与 D 重合时，AD 的长是(C) 2 A．3 B．4 C．8 D．9 9．下列说法：①斜边和一条直角边分别相等的两个直角三角形全等；②两个锐角分别 相等的两个直角三角形全等；③有一个角和底边分别相等的两个等腰三角形全等；④一条直 角边相等且另一条直角边上的中线相等的两个直角三角形全等．其中正确的有(B) A．1 个 B．2 个 C．3 个 D．4 个 10．如图，在△ABC 和△ADE 中，∠BAC＝∠DAE＝90°，AB＝AC，AD＝AE，点 C，D，E 在同一条直线上，连接 BD，BE.下列四个结论：①BD＝CE；②BD⊥CE；③∠ACE＋∠DBC＝45°； ④BE2＝2(AD2＋AB2)．其中结论正确的个数是(C) A．1 B．2 C．3 D．4 二、填空题(每小题 3 分，共 18 分) 11．(南通中考)一个等腰三角形的两边长分别为 4 cm 和 9 cm，则它的周长为 22cm. 12．如图，在 Rt△ABC 中，∠C＝90°，AD 平分∠BAC，交 BC 于点 D，CD＝4，则点 D 到 AB 的距离为 4. ,第 12 题图) ,第 13 题图) ,第 14 题图) 13．如图，已知点 B，C，F，E 在同一条直线上，∠1＝∠2，BC＝EF，要使△ABC≌△DEF， 还需添加一个条件，这个条件可以是 AC＝DF(答案不唯一)．(只需写出一个) 14．如图，△ABC 的周长为 22 cm，AB 的垂直平分线交 AC 于点 E，垂足为 D，若△BCE 的周长为 14 cm，则 AB＝8 cm. 15．如图，在△ABC 中，AC＝BC＝2，∠ACB＝90°，D 是 BC 边上的中点，E 是 AB 边上 一动点，则 EC＋ED 的最小值是 5. ,第 15 题图) ,第 16 题图) 16．(葫芦岛中考)如图，∠MON＝30°，点 B1 在边 OM 上，且 OB1＝2，过点 B1 作 B1A1⊥OM 交 ON 于点 A1，以 A1B1 为边在 A1B1 右侧作等边三角形 A1B1C1；过点 C1 作 OM 的垂线分别交 OM， ON 于点 B2，A2，以 A2B2 为边在 A2B2 的右侧作等边三角形 A2B2C2；过点 C2 作 OM 的垂线分别交 OM，ON 于点 B3，A3，以 A3B3 为边在 A3B3 的右侧作等边三角形 A3B3C3，…；按此规律进行下去， 则△AnAn＋1Cn 的面积为(3 2 )2n－2× 3 3 .(用含正整数 n 的代数式表示) 点拨：由题意△A1A2C1 是等边三角形，边长为2 3 3 ，△A2A3C2 是等边三角形，边长为3 2 ×2 3 3 ， △A3A4C3 是等边三角形，边长为3 2 ×3 2 ×2 3 3 ＝(3 2 )2×2 3 3 ，△A4A5C4 是等边三角形，边长为3 2 ×3 2 ×3 2 ×2 3 3 ＝(3 2 )3×2 3 3 ，…，△AnAn＋1Cn 的边长为(3 2 )n－1×2 3 3 ，∴△AnAn＋1Cn 的面积为 3 4 ×[(3 2 )n 3 －1×2 3 3 ]2＝(3 2 )2n－2× 3 3 三、解答题(共 72 分) 17．(6 分)如图，点 D，E 在△ABC 的 BC 边上，AB＝AC，AD＝AE.求证：BD＝CE. 证明：过点 A 作 AP⊥BC 于 P.∵AB＝AC，∴BP＝PC，∴AD＝AE，∴DP＝PE，∴BP－DP＝ PC－PE，∴BD＝CE 18．(7 分)(成都期末)如图，在△ABC 中，∠B＝30°，边 AB 的垂直平分线分别交 AB 和 BC 于点 D，E，且 AE 平分∠BAC. (1)求∠C 的度数；(3 分) (2)若 CE＝1，求 AB 的长．(4 分) 解：(1)∵DE 是线段 AB 的垂直平分线，∠B＝30°，∴∠BAE＝∠B＝30°，∵AE 平分∠ BAC，∴∠EAC＝∠BAE＝30°，即∠BAC＝60°，∴∠C＝180°－∠BAC－∠B＝180°－60° －30°＝90° (2)∵∠C＝90°，∠B＝30°，AE 平分∠BAC，CE＝1，∴AC＝ 3，∴AB＝2 3 19．(7 分)(达州期末)如图，在△ABC 中，AD 平分∠BAC，DE∥AC，EF⊥AD 交 BC 延长线 于 F.求证：∠FAC＝∠B. 证明：∵AD 平分∠BAC，∴∠BAD＝∠CAD，∵DE∥AC，∴∠EDA＝∠CAD，∴∠EDA＝∠ EAD，∴AE＝ED，又∵EF⊥AD，∴EF 是 AD 的垂直平分线，∴AF＝DF，∴∠FAD＝∠FDA.又∵ ∠FAD＝∠CAD＋∠FAC，∠FDA＝∠B＋∠BAD，∴∠FAC＝∠B 20．(7 分)如图，已知等腰三角形 ABC 中，AB＝AC，点 D，E 分别在边 AB，AC 上，且 AD ＝AE，连接 BE，CD，交于点 F. (1)判断∠ABE 与∠ACD 的数量关系，并说明理由；(3 分) (2)求证：过点 A，F 的直线垂直平分线段 BC.(4 分) 4 解：(1)∠ABE＝∠ACD.理由：在△ABE 和△ACD 中， AB＝AC， ∠A＝∠A， AE＝AD， ∴△ABE≌△ACD，∴∠ ABE＝∠ACD (2)连接 AF.∵AB＝AC，∴∠ABC＝∠ACB，由(1)可知∠ABE＝∠ACD，∴∠FBC＝∠FCB， ∴FB＝FC，∵AB＝AC，∴点 A，F 均在线段 BC 的垂直平分线上，即直线 AF 垂直平分线段 BC 21．(7 分)如图，在△ABC 中，∠A＝60°，点 D 是 BC 边的中点，DE⊥BC，∠ABC 的平 分线 BF 交 DE 于△ABC 内一点 P，连接 PC. (1)若∠ACP＝24°，求∠ABP 的度数；(4 分) (2)若∠ACP＝m°，∠ABP＝n°，请直接写出 m，n 满足的关系式：________________.(3 分) 解：(1)∵点 D 是 BC 边的中点，DE⊥BC，∴PB＝PC，∴∠PBC＝∠PCB.∵BP 平分∠ABC， ∴∠PBC＝∠ABP，∴∠PBC＝∠PCB＝∠ABP，∵∠A＝60°，∠ACP＝24°，∴∠PBC＋∠PCB ＋∠ABP＝180°－60°－24°， ∴3∠ABP＝120°－24°，∴∠ABP＝32° (2)m＋3n＝120 22．(8 分)如图，为了测出某塔 CD 的高度，在塔前的平地上选择一点 A，用测角仪测得 塔顶 D 的仰角为 30°，在 A，C 之间选择一点 B(A，B，C 三点在同一直线上)．用测角仪测 得塔顶 D 的仰角为 75°，且 AB 间的距离为 40 m. (1)求点 B 到 AD 的距离； (2)求塔高 CD.(结果用根号表示) 解：(1)过点 B 作 BE⊥AD，垂足为 E，∴∠AEB＝90°，又∵∠A＝30°，∴BE＝1 2 AB＝1 2 ×40 ＝20(m) (2)AE＝ AB2－BE2＝20 3，∵∠A＋∠ADB＝∠DBC＝75°，∴∠ADB＝75°－∠A＝45°， ∵BE⊥AD，∴∠BED＝90°，∴∠DBE＝∠ADB＝45°，∴DE＝BE＝20，∴AD＝AE＋DE＝20 3 5 ＋20，∵CD⊥AC，∴∠C＝90°，又∵∠A＝30°，∴CD＝1 2 AD＝1 2 (20 3＋20)＝(10 3＋10) m 23．(8 分)在△ABC 中，∠B＝22.5°，边 AB 的垂直平分线 DP 交 AB 于点 P，交 BC 于点 D，且 AE⊥BC 于点 E，DF⊥AC 于点 F，DF 与 AE 交于点 G，求证：EG＝EC. 解：如图所示： 连接 AD，∵∠B＝22.5°，且 DP 为 AB 的垂直平分线，∴DB＝DA，∴∠B＝∠BAD，∴∠ ADE＝2∠B＝45°，在 Rt△ADE 中，∠ADE＝45°，∴∠DAE＝45°，∴AE＝DE，∵AE⊥DE， ∴∠1＋∠2＝90°，∵DF⊥AC，∴∠2＋∠C＝90°，∴∠1＝∠C.在△DEG 和△AEC 中， ∠1＝∠C， ∠DEG＝∠AEC＝90°， DE＝AE， ∴△DEG≌△AEC(AAS)，∴EG＝EC 24．(10 分)如图，已知△ABC 是边长为 6 cm 的等边三角形，动点 P，Q 同时从 A，B 两 点出发，分别沿 AB，BC 方向匀速运动，其中点 P 运动的速度是 1 cm/s，点 Q 运动的速度是 2 cm/s，当点 Q 到达点 C 时，P，Q 两点都停止运动，设运动时间为 t s，解答下列问题： (1)当点 Q 到达点 C 时，PQ 与 AB 的位置关系如何？请说明理由； (2)在点 P 与点 Q 的运动过程中，△BPQ 是否能成为等边三角形？若能，请求出 t 的值； 若不能，请说明理由． 解：(1)当点 Q 到达点 C 时，PQ 与 AB 垂直，即△BPQ 为直角三角形．理由：∵AB＝AC ＝BC＝6 cm，∴当点 Q 到达点 C 时，AP＝3 cm，∴点 P 为 AB 的中点．∴QP⊥BA(等腰三角形 三线合一的性质) (2)假设在点 P 与点 Q 的运动过程中，△BPQ 能成为等边三角形，则有 BP ＝BQ，∴6－t＝2t，解得 t＝2，又∠B＝60°，∴当 t＝2 时，△BPQ 是等边三角形 6 25. (12 分)如图 1，已知点 B(0，6)，点 C 为 x 轴上一动点，连接 BC，△ODC 和△EBC 都是等边三角形． (1)求证：DE＝BO；(3 分) (2)如图 2，当点 D 恰好落在 BC 上时． ①求 OC 的长及点 E 的坐标；(3 分) ②在 x 轴上是否存在点 P，使△PEC 为等腰三角形？若存在，写出点 P 的坐标；若不存 在，说明理由；(3 分) ③如图 3，点 M 是线段 BC 上的动点(点 B，C 除外)，过点 M 作 MG⊥BE 于点 G，MH⊥CE 于点 H，当点 M 运动时，MH＋MG 的值是否发生变化？若不会变化，直接写出 MH＋MG 的值； 若会变化，简要说明理由．(3 分) (1)证明：∵△ODC 和△EBC 都是等边三角形，∴OC＝DC，BC＝CE，∠OCD＝∠BCE＝60°， ∴∠BCE＋∠BCD＝∠OCD＋∠BCD，即∠ECD＝∠BCO，∴△DEC≌△OBC(SAS)，∴DE＝BO (2)①∵△ODC 是等边三角形，∴∠OCB＝60°.∵∠BOC＝90°，∴∠OBC＝30°.设 OC ＝x，则 BC＝2x，∴x2＋62＝(2x)2，解得 x＝2 3，∴OC＝2 3，BC＝4 3.∵△EBC 是等边三 角形，∴BE＝BC＝4 3.又∵∠OBE＝∠OBC＋∠CBE＝90°，∴E(4 3，6) ②若点 P 在 C 点左侧，则 CP＝CE＝4 3，OP＝4 3－2 3＝2 3，点 P 的坐标为(－2 3， 0)；若点 P 在 C 点右侧，CP＝CE＝4 3，则 OP＝2 3＋4 3＝6 3，点 P 的坐标为(6 3，0)， 若 CP＝EP，∵∠DCO＝60°，∠BCE＝60°，∴∠ECP＝60°，∴△ECP 为等边三角形，∴CP ＝EP＝CE＝4 3，则 OP＝2 3＋4 3＝6 3，点 P 的坐标为(6 3，0)，综上，点 P 坐标为(－ 2 3，0)或(6 3，0) ③不会变化，MH＋MG＝6 第二章检测题 (时间：120 分钟 满分：120 分) 一、选择题(每小题 3 分，共 30 分) 1．已知实数 a，b 满足 a＋1＞b＋1，则下列选项错误的为(D) A．a＞b B．a＋2＞b＋2 C．－a＜－b D．2a＞3b 2．(海南中考)下列四个不等式组中，解集在数轴上表示如图所示的是(D) A. x≥2 x＞－3 B. x≤2 x＜－3 C. x≥2 x＜－3 D. x≤2 x＞－3 7 3．(株洲中考)下列哪个选项中的不等式与不等式 5x＞8＋2x 组成的不等式组的解集为8 3 ＜x＜5(C) A．x＋5＜0 B．2x＞10 C．3x－15＜0 D．－x－5＞0 4．不等式 6－4x≥3x－8 的非负整数解为(B) A．2 个 B．3 个 C．4 个 D．5 个 5．如果点 P(3－m，1)在第二象限，那么关于 x 的不等式(2－m)x＋2＞m 的解集是(B) A．x＞－1 B．x＜－1 C．x＞1 D．x＜1 6．(徐州中考)若函数 y＝kx＋b 的图象如图所示，则关于 x 的不等式 kx＋2b＜0 的解集 为(D) A．x＜3 B．x＞3 C．x＜6 D．x＞6 7．(聊城中考)已知不等式2－x 2 ≤2x－4 3 ＜x－1 2 ，其解集在数轴上表示正确的是(A) 8．已知关于 x 的不等式组 x－a≥b， 2x－a＜2b＋1 的解集为 3≤x＜5，则 a，b 的值为(A) A．a＝－3，b＝6 B．a＝6，b＝－3 C．a＝1，b＝2 D．a＝0，b＝3 9．已知在某超市内购物总金额超过 190 元时，购物总金额有打八折的优惠，安妮带 200 元到此超市买棒棒糖．若棒棒糖每根 9 元，则她最多可买多少根棒棒糖(C) A．22 B．23 C．27 D．28 10．某镇有甲，乙两家液化气站，它们每罐液化气的价格，质地和重量都相同．为了促 销，甲站的液化气每罐降价 25%销售；每个用户购买乙站的液化气，第 1 罐按照原价销售， 若用户继续购买，则从第 2 罐开始以 7 折优惠，促销活动都是一年．若小明家每年需购买 8 罐液化气，则购买液化气最省钱的方法是(B) A．买甲站的 B．买乙站的 C．买两站的都一样 D．先买甲站的 1 罐，以后买乙站的 二、填空题(每小题 3 分，共 18 分) 8 11．已知“x 的 3 倍大于 5，且 x 的一半与 1 的差不大于 2”，则 x 的取值范围是5 3 ＜x≤ 6. 12．(贵阳中考)已知关于 x 的不等式组 5－3x≥－1， a－x＜0 无解，则 a 的取值范围是 a≥2. 13．要使关于 x 的方程 5x－2m＝3x－6m＋1 的解在－3 与 4 之间，m 的取值范围是－7 4 ＜ m＜7 4 . 14．(白银中考)如图，一次函数 y＝－x－2 与 y＝2x＋m 的图象相交于点 P(n，－4)， 则关于 x 的不等式组 2x＋m＜－x－2， －x－2＜0 的解集为－2＜x＜2. 15．若关于 x，y 的二元一次方程组 2x＋y＝3k－1， x＋2y＝－2 的解满足 x＋y＞1，则 k 的取值范 围是 k＞2. 16．商店购进一批文具盒，进价每个 4 元，零售价每个 6 元，为促进销售，决定打折销 售，但利润率仍不低于 20%，那么该文具盒实际价格最多可打 8 折销售． 三、解答题(共 72 分) 17．(10 分)解下列不等式组，并把解集在数轴上表示出来： (1) 2（x＋1）≤x＋3， x－4＜3x； (2) 2x＞3x－2， 2x－1 3 ≥1 2 x－2 3 . 解：－2＜x≤1 解：－2≤x＜2 数轴表示略 数轴表示略 18．(6 分)已知关于 x，y 的方程组 5x＋2y＝11a＋18， 2x－3y＝12a－8 的解满足 x＞0，y＞0，求实数 a 的取值范围． 解：解方程组得 x＝3a＋2， y＝4－2a， ∵x＞0，y＞0，∴ 3a＋2＞0， 4－2a＞0， 解得－2 3 ＜a＜2 19．(6 分)小明解不等式1＋x 2 －2x＋1 3 ≤1 的过程如图．请指出他解答过程中错误步骤的 9 序号，并写出正确的解答过程． 解：错误的是①②⑤，正确解答过程如下：去分母，得 3(1＋x)－2(2x＋1)≤6，去括 号，得 3＋3x－4x－2≤6，移项，得 3x－4x≤6－3＋2，合并同类项，得－x≤5，两边都除 以－1，得 x≥－5 20．(6 分)x 取哪些整数值时，不等式 5x＋2＞3(x－1)与 1 2 x≤2－3 2 x 都成立？ 解：根据题意解不等式组 5x＋2＞3（x－1），① 1 2 x≤2－3 2 x，② 解不等式①，得 x＞－5 2 ，解不等式②， 得 x≤1，∴－5 2 ＜x≤1，故满足条件的整数有－2，－1，0，1 21．(7 分)某校九年级有三个班，其中九(一)班和九(二)班共有 105 名学生，在期末体 育测试中，这两个班级共有 79 名学生满分，其中九(一)班的满分率为 70%，九(二)班的满 分率为 80%. (1)求九(一)班和九(二)班各有多少名学生；(3 分) (2)该校九(三)班有 45 名学生，若九年级体育成绩的总满分率超过 75%，求九(三)班至 少有多少名学生体育成绩是满分．(4 分) 解：(1)设九(一)班有 x 名学生，九(二)班有 y 名学生，根据题意得 x＋y＝105， 70%x＋80%y＝79， 解得 x＝50， y＝55. 答：九(一)班有 50 名学生，九(二)班有 55 名学生 (2)设九(三)班有 m 名学生体育成绩满分，根据题意得 79＋m＞(105＋45)×75%，解得 m ＞33.5，∵m 为整数，∴m 的最小值为 34.答：九(三)班至少有 34 名学生体育成绩是满分 22．(7 分)若关于 x 的不等式组 x 2 ＋x＋1 3 ＞0， 3x＋5a＋4＞4（x＋1）＋3a 恰有三个整数解，求实数 a 的取值范围． 10 解：解不等式x 2 ＋x＋1 3 ＞0 得 x＞－2 5 ，解不等式 3x＋5a＋4＞4(x＋1)＋3a 得 x＜2a，∵ 不等式组恰有三个整数解，∴2＜2a≤3，∴1＜a≤3 2 23．(8 分)(达州期末)如图，在平面直角坐标系中，直线 L1：y＝－1 2 x＋6 分别与 x 轴， y 轴交于点 B，C，且与直线 L2：y＝1 2 x 交于点 A. (1)分别求出点 A，B，C 的坐标；(3 分) 解：(1)直线 L1：y＝－1 2 x＋6，当 x＝0 时，y＝6，当 y＝0 时，x＝12，则 B(12，0)， C(0，6)，解方程组 y＝－1 2 x＋6， y＝1 2 x 得 x＝6， y＝3， 则 A(6，3)，故 A(6，3)，B(12，0)，C(0，6) (2)直接写出关于 x 的不等式－1 2 x＋6＞1 2 x 的解集；(2 分) (3)若 D 是线段 OA 上的点，且△COD 的面积为 12，求直线 CD 的函数表达式．(3 分) 解：(2)关于 x 的不等式－1 2 x＋6＞1 2 x 的解集为 x＜6 (3)设 D(x，1 2 x)，∵△COD 的面积为 12，∴1 2 ×6×x＝12，解得 x＝4，∴D(4，2)，设直 线 CD 的函数表达式是 y＝kx＋b，把 C(0，6)，D(4，2)代入得 6＝b， 2＝4k＋b， 解得 k＝－1， b＝6， ∴ 直线 CD 的函数表达式为 y＝－x＋6 24．(10 分)甲、乙两商场以同样价格出售同样的商品，并且又各自推出不同的优惠方 案：在甲商场累计购物超过 100 元后，超出 100 元的部分按 90%收费；在乙商场累计购物超 过 50 元后，超出 50 元的部分按 95%收费，设小红在同一商场累计购物 x 元，其中 x＞100. (1)根据题意，填写下表(单位：元)：(3 分) 累计购物 实际花费 130 290 … x 在甲商场 127 271 … 11 在乙商场 126 … (2)当 x 取何值时，小红在甲、乙两商场的实际花费相同？(3 分) (3)当小红在同一商场累计购物超过 100 元时，在哪家商场的实际花费少？(4 分) 解：(1)100＋(x－100)×90% 278 50＋(x－50)×95% (2)根据题意得 100＋(x－100) ×90%＝50＋(x－50)×95%，解得 x＝150.即当 x＝150 时，小红在甲、乙两商场的实际花费 相同 (3)由 100＋(x－100)×90%＜50＋(x－50)×95%，解得 x＞150；由 100＋(x－100)× 90%＞50＋(x－50)×95%，解得 x＜150.∴当小红累计购物超过 150 元时，选择甲商场实际 花费少，当小红累计购物超过 100 元而不到 150 元时，选择乙商场实际花费少 25. (12 分)去冬今春，我市部分地区遭受了罕见的旱灾，“旱灾无情人有情”．某单位 给某乡中小学捐献一批饮用水和蔬菜共 320 件，其中饮用水比蔬菜多 80 件． (1)求饮用水和蔬菜各有多少件？ (2)现计划租用甲，乙两种货车共 8 辆，一次性将这批饮用水和蔬菜全部运往该乡中小 学．已知每辆甲种货车最多可装饮用水 40 件和蔬菜 10 件，每辆乙种货车最多可装饮用水和 蔬菜各 20 件，则运输部门安排甲，乙两种货车时有几种方案？请你帮助设计出来； (3)在(2)的条件下，如果甲种货车每辆需付运费 400 元，乙种货车每辆需付运费 360 元．运输部门应选择哪种方案可使运费最少？最少运费是多少元？ 解：(1)设饮用水有 x 件，则蔬菜有(x－80)件，由题意得 x＋(x－80)＝320，解得 x＝ 200，∴x－80＝120.则饮用水和蔬菜分别为 200 件和 120 件 (2)设租用甲种货车 m 辆，则 租用乙种货车(8－m)辆，由题意得 40m＋20（8－m）≥200， 10m＋20（8－m）≥120， 解得 2≤m≤4.∵m 为正整数， ∴m＝2 或 3 或 4.故安排甲、乙两种货车时有 3 种方案，设计方案分别为①甲车 2 辆，乙车 6 辆；②甲车 3 辆，乙车 5 辆；③甲车 4 辆，乙车 4 辆 (3)3 种方案的运费分别为①2×400 ＋6×360＝2960(元)；②3×400＋5×360＝3000(元)；③4×400＋4×360＝3040(元)；∴方 案①运费最少，最少运费是 2960 元．则运输部门应安排甲车 2 辆，乙车 6 辆，可使运费最 少，最少运费是 2960 元 第三章检测题 (时间：120 分钟 满分：120 分) 一、选择题(每小题 3 分，共 30 分) 1．在 A，B，C、D 四幅图案中，能通过图平移得到的是(B) 12 2．如图，下列四个图形中，△ABC 经过旋转之后不能得到△A′B′C′的是(D) 3．(天津中考)下列图形中，可以看作是中心对称图形的是(A) 4．(吉林中考)如图，将木条 a，b 与 c 钉在一起，∠1＝70°，∠2＝50°，要使木条 a 与 b 平行，木条 a 旋转的度数至少是(B) A．10° B．20° C．50° D．70° 5．一个图形无论经过平移还是旋转，下列说法：①对应线段相等；②对应线段平行； ③对应角相等；④图形的形状和大小都没有发生变化．其中正确的有(C) A．①②③ B．①②④ C．①③④ D．②③④ 6．如图，在平面直角坐标系中，若△ABC 与△A1B1C1 关于 E 点成中心对称，则对称中心 E 点的坐标是(A) A．(3，－1) B．(0，0) C．(2，－1) D．(－1，3) ,第 6 题图) ,第 7 题图) ,第 8 题图) 7．如图，将△ABC 沿射线 BC 向右平移到△DCE 的位置，连接 AD，则下列结论：①AB∥ CD；②AC＝DE；③AD＝BC；④∠B＝∠ADC；⑤△ACD≌△EDC.其中正确的结论有(A) A．5 个 B．4 个 C．3 个 D．2 个 8．如图，在 Rt△ABC 中，∠ACB＝90°，∠ABC＝60°，BC＝2.△A′B′C 可以由△ABC 绕点 C 顺时针旋转得到，其中点 A′与点 A 是对应点，点 B′与点 B 是对应点，连接 AB′， 且 A，B′，A′在同一条直线上，则 AA′的长为(A) A．6 B．4 3 C．3 3 D．3 9．如图，如果把△ABC 的顶点 A 先向下平移 3 格，再向左平移 1 格到达 A′点，连接 A′ B，那么线段 A′B 与线段 AC 的关系是(D) A．垂直 B .相等 C．平分 D．平分且垂直 13 ,第 9 题图) ,第 10 题图) 10．如图，△DEC 是由△ABC 经过了如下的几何变换而得到的：①以 AC 所在直线为对称 轴作轴对称，再以 C 为旋转中心，顺时针旋转 90°；②以 C 为旋转中心，顺时针旋转 90° 得△A′B′C′，再以 A′C′所在直线为对称轴作轴对称；③将△ABC 向下向左各平移 1 个 单位长度，再以 AC 的中点为中心作中心对称，其中正确的变换有(A) A．①② B．①③ C．②③ D．①②③ 二、填空题(每小题 3 分，共 18 分) 11．(长沙中考)在平面直角坐标系中，将点 A(－2，3)向右平移 3 个单位长度，再向下 平移 2 个单位长度，那么平移后对应的点 A′的坐标是(1，1)． 12．如图，已知面积为 1 的正方形 ABCD 的对角线相交于点 O，过点 O 任作一条直线分 别交 AD，BC 于 E，F，则阴影部分的面积是1 4 . ,第 12 题图) ,第 13 题图) ,第 14 题图) 13．如图，△A′B′C′是由△ABC 沿 BC 方向平移得到的，若 BC＝5 cm，AC＝4.5 cm， B′C＝2 cm，那么 A′C′＝4.5cm，A，A′两点之间的距离为 3cm. 14．如图，在△ABC 中，∠BAC＝115°，∠ACB＝25°，把△ABC 以 AC 为对称轴作对称 变换得△ADC，又把△ABC 绕点 B 逆时针旋转 55°得△FBE，则∠α的度数为 145°. 15．如图，在△ABC 中，∠ACB＝90°，∠BAC＝30°，将△ABC 绕点 C 按逆时针方向旋 转α(0°＜α＜90°)后得到△DEC，设 CD 交 AB 于点 F，连接 AD，当旋转角α的度数为 40° 或 20°时，△ADF 是等腰三角形． ,第 15 题图) ,第 16 题图) 16．在如图所示的平面直角坐标系中，△OA1B1 是边长为 2 的等边三角形，作△B2A2B1 与 △OA1B1 关于点 B1 成中心对称，再作△B2A3B3 与△B2A2B1 关于点 B2 成中心对称，如此作下去， 则△B2nA2n＋1B2n＋1(n 是正整数)的顶点 A2n＋1 的坐标是 (4n＋1， 3) . 三、解答题(共 72 分) 17．(6 分)如图，将△ABC 沿直线 AB 向右平移后到达△BDE 的位置． (1)若 AC＝6 cm，则 BE＝________cm； (2)若∠CAB＝50°，∠BDE＝100°，求∠CBE 的度数． 14 解：(1)6 (2)根据平移的性质得 AC∥BE，∠ABC＝∠BDE＝100°，∴∠C＝180°－∠CAB－∠ABC ＝180°－50°－100°＝30°，由 AC∥BE 得∠CBE＝∠C＝30° 18．(6 分)如图，已知 AD＝AE，AB＝AC. (1)求证：∠B＝∠C； (2)若∠A＝50°，问△ADC 经过怎样的变换能与△AEB 重合？ (1)证明：在△AEB 与△ADC 中，AB＝AC，∠A＝∠A，AE＝AD，∴△AEB≌△ADC，∴∠B ＝∠C (2)解：先将△ADC 绕点 A 逆时针旋转 50°，再将△ADC 沿直线 AE 对折，即可得△ADC 与△AEB 重合．或先将△ADC 绕点 A 顺时针旋转 50°，再将△ADC 沿直线 AB 对折，即可得△ ADC 与△AEB 重合 19．(7 分)如图，边长为 4 的正方形 ABCD 绕点 D 旋转 30°后能与四边形 A′B′C′D 重合． (1)旋转中心是哪一点？(1 分) (2)四边形 A′B′C′D 是什么图形？面积是多少？(2 分) (3)求∠C′DC 和∠CDA′的度数；(2 分) (4)连接 AA′，求∠DAA′的度数．(2 分) 解：(1)点 D (2)四边形 A′B′C′D 是正方形，面积为 4×4＝16 (3)由题意得∠C′DC＝30°，∠CDA′＝90°－∠C′DC＝60° (4)∵AD＝A′D，∠ADA′＝30°，∴∠DAA′＝(180°－30°)×1 2 ＝75° 20．(7 分)(1)在平面直角坐标系中找出点 A(－3，4)，B(－4，1)，C(－1，1)，D(－2， 3)并将它们依次连接；(2 分) (2)将(1)中所画图形先向右平移 4 个单位，再向下平移 3 个单位，画出第二次平移后的 图形；(2 分) (3)如何将(1)中所画图形经过一次平移得到(2)中所画图形？平移前后对应点的横坐标 有什么关系？纵坐标呢？(3 分) 15 解：(1)画图略 (2)画图略 (3)将 A 点与它的对应点 A′连接起来，则 AA′＝ 32＋42 ＝5，∴将(1)中所画图形沿 A 到 A′的方向平移 5 个单位长度得到(2)中所画图形．四边形 A′ B′C′D′与四边形 ABCD 相比，对应点的横坐标分别增加了 4，纵坐标分别减少了 3 21．(7 分)(枣庄中考)如图，在 4×4 的方格纸中，△ABC 的三个顶点都在格点上． (1)在图 1 中，画出一个与△ABC 成中心对称的格点三角形；(2 分) (2)在图 2 中，画出一个与△ABC 成轴对称且与△ABC 有公共边的格点三角形；(2 分) (3)在图 3 中，画出△ABC 绕着点 C 按顺时针方向旋转 90°后的三角形．(3 分) 解：(1)如图①所示，△DCE 为所求作 (2)如图②所示，△ACD 为所求作 (3)如图③所示，△ECD 为所求作 22．(8 分)如图，在△ABC 中，∠BAC＝120°，以 BC 为边向图形外作等边△BCD，把△ ABD 绕点 D 按顺时针方向旋转 60°到△ECD 的位置，若 AB＝3，AC＝2. (1)求∠BAD 的度数； (2)求 AD 的长． 解：(1)因为△DCE 是由△DBA 旋转后得到的，∴DE＝DA，∵∠BDC＝60°，∴∠ADE＝60°， ∴△ADE 是等边三角形，∴∠DAE＝60°，∠BAD＝∠BAC－∠DAE＝120°－60°＝60° (2)AD＝AE＝AC＋CE＝AC＋AB＝2＋3＝5 23．(9 分)如图 1，在△ABC 中，AC＝BC，∠A＝30°，点 D 在 AB 边上，且∠ADC＝45°. (1)求∠BCD 的度数；(3 分) (2)将图 1 中的△BCD 绕点 B 顺时针旋转得到△BC′D′，当点 D′恰好落在 BC 边上时， 如图 2 所示，连接 C′C 并延长交 AB 于点 E. ①求∠C′CB 的度数；(3 分) 16 ②求证：△C′BD′≌△CAE.(3 分) 解：(1)∵AC＝BC，∠A＝30°，∴∠B＝∠A＝30°.∵∠ADC＝45°，∴∠BCD＝∠ADC －∠B＝15° (2)①由旋转，得 BC＝BC′＝AC，∠C′BD′＝∠CBD＝∠A＝30°.∴∠CC′B＝∠C′CB ＝75° ②证明：∵∠CEB＝∠C′CB－∠CBA＝45°，∴∠ACE＝∠CEB－∠A＝15°.∴∠BC′D′ ＝∠BCD＝∠ACE.在△C′BD′和△CAE 中， ∠BC′D′＝∠ACE， BC′＝AC， ∠C′BD′＝∠A， ∴△C′BD′≌△CAE(ASA) 24．(10 分)如图，在平面直角坐标系 xOy 中，已知 Rt△DOE，∠DOE＝90°，OD＝3，点 D 在 y 轴上，点 E 在 x 轴上，在△ABC 中，点 A，C 在 x 轴上，AC＝5，∠ACB＋∠ODE＝180°， ∠ABC＝∠OED，BC＝DE.按下列要求画图(保留作图痕迹)： (1)将△ODE 绕 O 点按逆时针方向旋转 90°得到△OMN(其中点 D 的对应点为点 M，点 E 的对应点为点 N)，画出△OMN；(3 分) (2)将△ABC 沿 x 轴向右平移得到△A′B′C′(其中 A，B，C 的对应点分别为点 A′，B′， C′)，使得 B′C′与(1)中△OMN 的边 NM 重合；(3 分) (3)求 OE 的长．(4 分) 解： (1)△OMN 如图所示 (2)△A′B′C′如图所示 (3)设 OE＝x，则 ON＝x，作 MF⊥A′B′于点 F，由作图可知 B′C′平分∠A′B′O，且 C′O⊥OB′，∴B′F＝B′O＝OE＝x，FC′＝OC′＝OD＝3.∵A′C′＝AC＝5，∴A′F＝ 52－32＝4，∴A′B′＝x＋4，A′O＝5＋3＝8.在 Rt△A′B′O 中，x2＋82＝(4＋x)2，解得 x＝6，即 OE＝6 25. (12 分)如图，小明将一张长方形纸片沿对角线剪开，得到两张三角形纸片(如图②)， 量得它们的斜边长为 10 cm，较小的锐角为 30°，再将这两张三角形纸片摆成如图③的形状， 且点 B，C，F，D 在同一条直线上，且点 C 与点 F 重合(在图③至图⑥中统一用 F 表示)． 小明在对这两张三角形纸片进行如下操作时遇到了三个问题，请你帮忙解决： 17 (1)将图③中的△ABF 沿 BD 向右平移到图④的位置，使点 B 与点 F 重合，请你求出平移 的距离； (2)将图③中的△ABF 绕点 F 顺时针方向旋转 30°到图⑤的位置，A1F 交 DE 于点 G，请 你求出线段 FG 的长度； (3)将图③中的△ABF 沿直线 AF 翻折到图⑥的位置，AB1 交 DE 于点 H，请证明：AH＝DH. 解：(1)图形平移的距离就是线段 BC 的长，∵在 Rt△ABC 中，斜边长为 10 cm，∠BAC ＝30°，∴BC＝5 cm.∴平移的距离为 5 cm (2)∵∠A1FA＝30°，∴∠GFD＝60°，又∵∠D＝30°，∴∠FGD＝90°.在 Rt△DFG 中， 由勾股定理得 FD＝5 3 cm，∴FG＝1 2 FD＝5 3 2 cm (3)在△AHE 与△DHB1 中，∵∠FAB1＝∠EDF＝30°，FD＝FA，EF＝FB＝FB1，∴FD－FB1 ＝FA－FE，即 AE＝DB1.又∵∠AHE＝∠DHB1.∴△AHE≌△DHB1(AAS)．∴AH＝DH 期中检测题 (时间：120 分钟 满分：120 分) 一、选择题(每小题 3 分，共 30 分) 1．(达州中考)下列图形中是中心对称图形的是(B) 2．(达州月考)已知 x＞y，下列不等式一定成立的是(C) A．ax＞ay B．3x＜3y C．－2x＜－2y D．a2x＞a2y 3．(益阳中考)不等式组 2x＋1＜3， 3x＋1≥－2 的解集在数轴上表示正确的是(A) 18 4．在平面直角坐标系中，线段 AB 的两个端点坐标分别为 A(－1，－1)，B(1，2)，平 移线段 AB，得到线段 A′B′，已知 A′的坐标为(3，－1)，则点 B′的坐标为(B) A．(4，2) B．(5，2) C．(6，2) D．(5，3) 5．如图，在△ABC 中，∠CAB＝75°，在同一平面内，将△ABC 绕点 A 旋转到△AB′C′ 的位置，使得 CC′∥AB，则∠BAB′等于(A) A．30° B．35° C．40° D．50° ,第 5 题图) ,第 6 题图) ,第 7 题 图) 6．在△ABC 中，∠C＝90°，AD 平分∠BAC，DE 垂直平分 AB，垂足为 E.若 CD＝2，则 BD 的长为(C) A．2 B．3 C．4 D．5 7．如图，AD⊥CD，AE⊥BE，垂足分别为 D，E，且 AB＝AC，AD＝AE.则下列结论：①△ ABE≌△ACD；②AM＝AN；③△ABN≌△ACM；④BO＝EO.其中正确的有(B) A．4 个 B．3 个 C．2 个 D．1 个 8．如图，函数 y1＝－2x 与 y2＝ax＋3 的图象相交于点 A(m，2)，则关于 x 的不等式－ 2x＞ax＋3 的解集是(D) A．x＞2 B．x＜2 C．x＞－1 D．x＜－1 ,第 8 题图) ,第 9 题图) ,第 10 题图) 9．如图，已知 MN 是△ABC 的边 AB 的垂直平分线，垂足为点 F，∠CAB 的平分线 AD 交 BC 于点 D，且 MN 与 AD 交于点 O，连接 BO 并延长交 AC 于点 E，则下列结论中不一定成立的 是(B) A．∠CAD＝∠BAD B．OE＝OF C．AF＝BF D．OA＝OB 10．如图，在等边△ABC 中，D 是边 AC 上一点，连接 BD，将△BCD 绕点 B 逆时针旋转 60°，得到△BAE，连接 ED，若 BC＝5，BD＝4，则下列结论错误的是(B) A．AE∥BC B．∠ADE＝∠BDC C．△BDE 是等边三角形 D．△ADE 的周长是 9 二、填空题(每小题 3 分，共 18 分) 11．(长春中考)如图，在△ABC 中，AB＝AC.以点 C 为圆心，以 CB 长为半径作圆弧，交 AC 的延长线于点 D，连结 BD.若∠A＝32°，则∠CDB 的大小为 37 度． ,第 11 题图) ,第 13 题图) 19 ,第 15 题图) 12．(兰州中考)不等式组 2（x＋1）≥5x－7， 4 3 x＋3＞1－2 3 x， 的解集为－1＜x≤3. 13．如图，在△ABC 中，∠C＝90°，AB＝5，AD 是△ABC 的角平分线，若 CD＝ 3，则 △ABD 的面积为5 3 2 . 14．一次生活常识竞赛一共有 25 道题，答对一题得 4 分，不答得 0 分，答错一题扣 2 分，小明有 2 题没答，竞赛成绩要超过 74 分，则小明最多答错 3 道题． 15．如图，点 E 是正方形 ABCD 内的一点，连接 AE，BE，CE，将△ABE 绕点 B 顺时针旋 转 90°到△CBE′的位置．若 AE＝1，BE＝2，CE＝3，则∠BE′C＝135°. 16．如图，在△ABC 中，∠ACB＝90°，AC＝BC，O 是 AB 的中点，点 D 在 AC 上，点 E 在 BC 上，且∠DOE＝90°.则下列结论：①OA＝OB＝OC；②CD＝BE；③△ODE 是等腰直角三 角形；④四边形 CDOE 的面积等于△ABC 的面积的一半；⑤AD2＋BE2＝2OD2；⑥CD＋CE＝ 2OA. 其中正确的有①②③④⑤⑥.(填序号) 三、解答题(共 72 分) 17．(6 分)解不等式组 1 2 （x＋1）≤2， x＋2 2 ≥x＋3 3 . 解：解不等式1 2 (x＋1)≤2，得 x≤3，解不等式x＋2 2 ≥x＋3 3 ，得 x≥0，则不等式组的解 集为 0≤x≤3 18．(6 分)如图，△ABO 与△CDO 关于 O 点成中心对称，点 E，F 在线段 AC 上，且 AF＝ CE.求证：FD＝BE. 解：根据中心对称的性质可得 BO＝DO，AO＝CO，又∵AF＝CE，∴AO－AF＝CO－CE，即 OF＝OE.在△ODF 和△OBE 中，DO＝BO，∠DOF＝∠BOE(对顶角相等)，OF＝OE，∴△ODF≌△ OBE(SAS)，∴FD＝BE 19．(6 分)如图，在△ABC 中，∠C＝90°，AD 平分∠CAB，交 CB 于点 D，过点 D 作 DE 20 ⊥AB 于点 E. (1)求证：△ACD≌△AED； (2)若∠B＝30°，CD＝1，求 BD 的长． 解：(1)∵AD 平分∠CAB，∴∠CAD＝∠EAD，∵∠C＝90°，DE⊥AB，∴∠C＝∠DEA＝90°， 又∵AD＝AD，∴△ACD≌△AED(AAS) (2)∵DE⊥AB，∴∠DEB＝90°，又∵由(1)得△ACD≌△AED，∴DE＝CD＝1，在 Rt△BDE 中，∵∠B＝30°，∴BD＝2DE＝2 20．(8 分)如图，OA⊥OB，OA＝45 海里，OB＝15 海里，我国某岛位于 O 点，我国渔政 船在点 B 处发现有一艘不明国籍的渔船，自 A 点出发沿着 AO 方向匀速驶向该岛所在地 O 点， 我国渔政船立即从 B 处出发以相同的速度沿某直线去拦截这艘渔船，结果在点 C 处截住了渔 船． (1)请用直尺和圆规作出 C 处的位置； (2)求我国渔政船行驶的航程 BC 的长. 解： (1)如答图，连接 AB，作 AB 的垂直平分线与 OA 交于点 C.点 C 即为所求 (2)连接 BC， 设 BC＝x 海里，则 CA＝x 海里，OC＝(45－x)海里，在 Rt△OBC 中，BO2＋OC2＝BC2，即 152 ＋(45－x)2＝x2，解得 x＝25.则我国渔政船行驶的航程 BC 为 25 海里 21．(8 分)如图，在平面直角坐标系中，Rt△ABC 的三个顶点分别是 A(－4，2)，B(0， 4)，C(0，2)． (1)将△ABC 以点 C 为旋转中心旋转 180°，画出旋转后对应的△A1B1C；平移△ABC，若 点 A 的对应点 A2 的坐标为(0，－4)，画出平移后对应的△A2B2C2； (2)若将△A1B1C 绕某一点旋转可以得到△A2B2C2；请直接写出旋转中心的坐标． 21 解：(1)图略 (2)(2，－1) 22．(8 分)如图，下列 4×4 网格图都是由 16 个相同小正方形组成，每个网格图中有 4 个小正方形已涂上阴影，请在空白小正方形中，按下列要求涂上阴影． (1)在图 1 中选取 2 个空白小正方形涂上阴影，使 6 个阴影小正方形组成一个中心对称 图形； (2)在图 2 中选取 2 个空白小正方形涂上阴影，使 6 个阴影小正方形组成一个轴对称图 形，但不是中心对称图形． 解：(1)答案如图所示： (2)答案如图所示： 23．(8 分)(贺州中考)某自行车经销商计划投入 7.1 万元购进 100 辆 A 型和 30 辆 B 型 自行车，其中 B 型车单价是 A 型车单价的 6 倍少 60 元． (1)求 A，B 两种型号的自行车单价分别是多少元？ (2)后来由于该经销商资金紧张，投入购车的资金不超过 5.86 万元，但购进这批自行车 的总数不变，那么至多能购进 B 型车多少辆？ 解：(1)设 A 型自行车的单价为 x 元/辆，B 型自行车的单价为 y 元/辆，根据题意得 y＝6x－60， 100x＋30y＝71000， 解得 x＝260， y＝1500. 答：A 型自行车的单价为 260 元/辆，B 型自行车的单价 为 1500 元/辆 (2)设购进 B 型自行车 m 辆，则购进 A 型自行车(130－m)辆，根据题意得 260(130－m) ＋1500m≤58600，解得 m≤20.答：至多能购进 B 型车 20 辆 22 24．(10 分)已知△ABC 是等边三角形，将一块含有 30°角的直角三角板 DEF 如图放置， 让三角板在 BC 所在的直线上向右平移．如图①，当点 E 与点 B 重合时，点 A 恰好落在三角 形的斜边 DF 上． (1)利用图①证明：EF＝2BC； (2)在三角板的平移过程中，在图②中线段 EB＝AH 是否始终成立(假定 AB，AC 与三角板 斜边的交点为 G，H)？如果成立，请证明；如果不成立，请说明理由． 解：(1)∵△ABC 是等边三角形，∴∠ACB＝60°，AC＝BC.∵∠F＝30°，∴∠CAF＝60° －30°＝30°，∴∠CAF＝∠F，∴CF＝AC.∴CF＝AC＝BC，∴EF＝2BC (2)成立．∵△ABC 是等边三角形，∴∠ACB＝60°，AC＝BC，∵∠F＝30°，∴∠CHF＝ 60°－30°＝30°.∴∠CHF＝∠F.∴CH＝CF.∵EF＝2BC，∴EB＋CF＝BC.又∵AH＋CH＝AC， AC＝BC，∴EB＝AH 25. (12 分)如图 1，已知 Rt△ABC 中，AB＝BC，AC＝2，把一块含 30°角的三角板 DEF 的直角顶点 D 放在 AC 的中点上(直角三角板的短直角边为 DE，长直角边为 DF)，点 C 在 DE 上，点 B 在 DF 上． (1)求重叠部分△BCD 的面积； (2)如图 2，将直角三角板 DEF 绕 D 点按顺时针方向旋转 30 度，DE 交 BC 于点 M，DF 交 AB 于点 N. ①求证：DM＝DN； ②在此条件下重叠部分的面积会发生变化吗？若发生变化，请求出重叠部分的面积，若 不发生变化，请说明理由； (3)如图 3，将直角三角板 DEF 绕 D 点按顺时针方向旋转α度(0＜α＜90)，DE 交 BC 于 点 M，DF 交 AB 于点 N，则 DM＝DN 的结论仍成立吗？重叠部分的面积会变吗？(请直接写出 结论，不需要说明理由) 解：(1)∵AB＝BC，AC＝2，D 是 AC 的中点，∴CD＝BD＝1 2 AC＝1，BD⊥AC.∴S△BCD＝1 2 CD·BD ＝1 2 ×1×1＝1 2 (2)①证明：连接 BD，则 BD 垂直平分 AC.∴BD＝CD，∠C＝∠NBD＝45°.由题意可知∠ EDC＝30°，∴∠NDA＝60°，∵BD 垂直平分 AC，∴∠BDA＝90°，∴∠BDN＝∠BDA－∠NDA 23 ＝30°，∴∠CDM＝∠BDN，∴△CDM≌△BDN(ASA)．∴DM＝DN ②由①知△CDM≌△BDN，∴S 四边形 BNDM＝S△BCD＝1 2 ，即此条件下重叠部分的面积不变，仍为 1 2 (3)DM＝DN 的结论仍成立，重叠部分的面积不会变 第四章检测题 (时间：120 分钟 满分：120 分) 一、选择题(每小题 3 分，共 30 分) 1．下列从左边到右边的变形，属于因式分解的是(C) A．(3－x)(3＋x)＝9－x2 B．(y＋1)(y－3)＝－(3－y)(y＋1) C．m4－n4＝(m2＋n2)(m＋n)(m－n) D．4yz－2y2z＋z＝2y(2z－yz)＋z 2．下列各组多项式中，没有公因式的是(D) A．(a－b)3 与(a－b)2 B．3m(x－y)与 n(y－x) C．2(a－3)2 与－a＋3 D．ax2＋by2 与 ax＋by 3．下列各式中，能用公式法分解因式的有(B) ①－x2－y2；②－1 4 a2b2＋1；③a2＋ab＋b2；④－x2＋2xy－y2；⑤1 4 －mn＋m2n2. A．2 个 B．3 个 C．4 个 D．5 个 4．(安徽中考)下列分解因式正确的是(C) A．－x2＋4x＝－x(x＋4) B．x2＋xy＋x＝x(x＋y) C．x(x－y)＋y(y－x)＝(x－y)2 D．x2－4x＋4＝(x＋2)(x－2) 5．一次数学课堂练习，小明同学做了如下四道因式分解题．你认为小明做得不够完整 的一题是(B) A．4x2－4x＋1＝(2x－1)2 B．x3－x＝x(x2－1) C．x2y－xy2＝xy(x－y) D．x2－y2＝(x＋y)(x－y) 6．小明用四张如图所示的纸片拼成一个大长方形，并据此写出一个多项式的因式分解， 正确的是(D) A．x2＋2x＝x(x＋2) B．x2－2x＋1＝(x－1)2 24 C．x2＋2x＋1＝(x＋1)2 D．x2＋3x＋2＝(x＋2)(x＋1) 7．已知多项式 2x2＋bx＋c 因式分解后为 2(x－3)(x＋1)，则 b，c 的值为(D) A．b＝3，c＝－1 B．b＝－6，c＝2 C．b＝－6，c＝－4 D．b＝－4，c＝－6 8．计算(－2)99＋(－2)100 的结果为(A) A．299 B．2100 C．－299 D．－2 9．对于任何整数 m，多项式(4m＋5)2－9 都能(A) A．被 8 整除 B．被 m 整除 C．被(m－1)整除 D．被(2m－1)整除 10．若三角形的三边长分别是 a，b，c，且满足 a2b－a2c＋b2c－b3＝0，则这个三角形是 (A) A．等腰三角形 B．直角三角形 C．等边三角形 D．三角形的形状不确定 二、填空题(每小题 3 分，共 18 分) 11．(潍坊中考)因式分解：(x＋2)x－x－2＝(x＋2)(x－1)． 12．(菏泽中考)若 a＋b＝2，ab＝－3，则代数式 a3b＋2a2b2＋ab3 的值为－12. 13．若多项式(3x＋2)(2x－5)＋(5－2x)(2x－1)可分解为(2x＋m)(x＋n)，其中 m，n 均为整数，则 mn 的值为－15. 14．计算：1.222×9－1.332×4＝6.32. 15．已知代数式 a2＋2a＋2，当 a＝－1 时，它有最小值，最小值为 1. 16．从边长为 a 的正方形纸板中挖去一个边长为 b 的小正方形纸板后，将其裁成四个相 同的等腰梯形，如图甲，然后拼成一个平行四边形，如图乙，那么通过计算两个图形阴影部 分的面积，可以验证成立的为 a2－b2＝(a＋b)(a－b)． 三、解答题(共 72 分) 17．(12 分)将下列各式分解因式： (1)2x2y－8xy＋8y; (2)a2(x－y)－9b2(x－y)； 解：2y(x－2)2 解：(x－y)(a＋3b)(a－3b) (3)(a＋b)3－4(a＋b); (4)(y2－1)2＋6(1－y2)＋9. 解：(a＋b)(a＋b＋2)(a＋b－2) 解：(y＋2)2(y－2)2 18．(8 分)先分解因式，再求值： 25 (1)已知 x－y＝－2 3 ，求(x2＋y2)2－4xy(x2＋y2)＋4x2y2 的值； 解：原式＝(x－y)4，当 x－y＝－2 3 时，原式＝16 81 (2)已知 x＋y＝1，xy＝－1 2 ，求 x(x＋y)(x－y)－x(x＋y)2 的值． 解：原式＝－2xy(x＋y)，当 x＋y＝1，xy＝－1 2 时，原式＝－2×(－1 2 )×1＝1 19．(6 分)下列三个多项式：1 2 x3＋2x2－x，1 2 x3＋4x2＋x，1 2 x3－2x2，请选择你喜欢的两 个多项式进行加法运算，再将结果因式分解． 解：1 2 x3＋2x2－x＋1 2 x3＋4x2＋x＝x3＋6x2＝x2(x＋6)(答案不唯一) 20．(6 分)甲，乙两同学分解因式 x2＋mx＋n，甲看错了 n，分解结果为(x＋2)(x＋4)； 乙看错了 m，分解结果为(x＋1)(x＋9)，请分析一下 m，n 的值及正确的分解过程． 解：∵(x＋2)(x＋4)＝x2＋6x＋8，甲看错了 n 的值，∴m＝6，又∵(x＋1)(x＋9)＝x2 ＋10x＋9，乙看错了 m 的值，∴n＝9，∴原式为 x2＋6x＋9＝(x＋3)2 21．(7 分)(大连中考)【观察】1×49＝49，2×48＝96，3×47＝141，…，23×27＝621， 24×26＝624，25×25＝625，26×24＝624，27×23＝621，…，47×3＝141，48×2＝96， 49×1＝49. 【发现】根据你的阅读回答问题： (1)上述内容中，两数相乘，积的最大值为________；(1 分) (2)设参与上述运算的第一个因数为 a，第二个因数为 b，用等式表示 a 与 b 的数量关系 是____________．(2 分) 【类比】观察下列两数的积：1×59，2×58，3×57，4×56，…，m×n，…，56×4， 57×3，58×2，59×1. 猜想 mn 的最大值为________，(2 分)并用你学过的知识加以证明．(2 分) 解：【发现】(1)625 (2)a＋b＝50 【类比】900.证明如下：由题意，可得 m＋n＝60，将 n＝60－m 代入 mn，得 mn＝－m2 26 ＋60m＝－(m－30)2＋900，∴m＝30 时，mn 的最大值为 900 22．(7 分)阅读下列解题过程： 已知 a，b，c 为三角形的三边，且满足 a2c2－b2c2＝a4－b4，试判断△ABC 的形状． 解：∵a2c2－b2c2＝a4－b4， (A) ∴c2(a2－b2)＝(a2＋b2)(a2－b2), (B) 则 c2＝a2＋b2, (C) ∴△ABC 为直角三角形. (D) (1)上述解题过程中，从哪一步开始出现错误？请写出该步的代号________；(1 分) (2) 错 误 的 原 因 ________________________________________________________________________；(2 分) (3)请写出正确的解答过程．(4 分) 解：(1)C (2)忽略了 a2－b2＝0，即 a＝b 的可能 (3)∵a2c2－b2c2＝a4－b4，∴c2(a2－b2)＝(a2＋b2)(a2－b2)，即 c2(a2－b2)－(a2＋b2)(a2－ b2)＝0，∴(a2－b2)(c2－a2－b2)＝0，∴a2－b2＝0 或 c2－a2－b2＝0，即 a＝b 或 c2＝a2＋b2， ∴△ABC 为等腰三角形或直角三角形 23．(8 分)如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神 秘数”．如：4＝22－02，12＝42－22，20＝62－42，因此 4，12，20 都是“神秘数”． (1)28 和 2020 这两个数是“神秘数”吗？为什么？(2 分) (2)设两个连续偶数为 2k＋2 和 2k(其中 k 取非负整数)，由这两个连续偶数构造的“神 秘数”是 4 的倍数吗？为什么？(3 分) (3)两个连续奇数的平方差(取正数)是“神秘数”吗？为什么？(3 分) 解：(1)因为 28＝82－62，2020＝5062－5042，所以 28 和 2020 都是“神秘数” (2)(2k＋2)2－(2k)2＝4(2k＋1)，因此由 2k＋2 和 2k 构造的“神秘数”是 4 的倍数 (3)由(2)知“神秘数”可表示为 4 的倍数但一定不是 8 的倍数．设两个连续奇数为 2k ＋1 和 2k－1，则(2k＋1)2－(2k－1)2＝8k，所以两个连续奇数的平方差不是“神秘数” 24．(8 分)有足够多的长方形和正方形的卡片，如图① 27 (1)如果选取 1 号，2 号，3 号卡片分别为 1 张，2 张，3 张(如图②)，可拼成一个长方 形(不重叠无缝隙)．请画出这个长方形的草图，并运用拼图前后面积之间的关系将多项式 a2＋3ab＋2b2 分解因式； (2)小明想用类似的方法将多项式 2a2＋7ab＋3b2 分解因式，那么需要 1 号卡片________ 张，2 号卡片________张，3 号卡片________张．试画出草图，写出将多项式 2a2＋7ab＋3b2 分解因式的结果． 解：(1)画图略．a2＋3ab＋2b2＝(a＋b)(a＋2b) (2)2 3 7.画图略.2a2＋7ab＋3b2＝(2a＋b)(a＋3b) 25. (10 分)阅读材料：若 m2－2mn＋2n2－8n＋16＝0，求 m，n 的值． 解：∵m2－2mn＋2n2－8n＋16＝0，∴(m2－2mn＋n2)＋(n2－8n＋16)＝0， ∴(m－n)2＋(n－4)2＝0，又∵(m－n)2≥0，(n－4)2≥0， ∴ （m－n）2＝0 （n－4）2＝0 ，解得 m＝4， n＝4. 请解答下面的问题： (1)已知 x2－2xy＋2y2＋6y＋9＝0，求 xy－x2 的值；(3 分) (2)已知△ABC 的三边长 a，b，c 都是互不相等的正整数，且满足 a2＋b2－4a－18b＋85 ＝0，求△ABC 的最长边 c 的值；(3 分) (3)已知 a2＋b2＝12，ab＋c2－16c＋70＝0，求 a＋b＋c 的值．(4 分) 解：(1)∵x2－2xy＋2y2＋6y＋9＝0，∴(x－y)2＋(y＋3)2＝0，解得 y＝－3，故 x＝y＝ －3，xy－x2＝－3×(－3)－(－3)2＝9－9＝0 (2)∵a2＋b2－4a－18b＋85＝0，∴(a－2)2＋(b－9)2＝0，解得 a＝2，b＝9，∴7＜c＜ 11，∵△ABC 的三边长 a，b，c 都是互不相等的正整数，∴△ABC 的最长边 c 的值为 10 (3)∵a2＋b2＝12，∴(a＋b)2－2ab＝12，∴ab＝1 2 (a＋b)2－6，∴ab＋c2－16c＋70＝0， 1 2 (a＋b)2－6＋(c－8)2＋6＝0，则1 2 (a＋b)2＋(c－8)2＝0，则 c＝8，a＋b＝0，∴a＋b＋c＝8 第五章检测题 (时间：120 分钟 满分：120 分) 28 一、选择题(每小题 3 分，共 30 分) 1．在式子1 a ，2xy π ，3ab2c 4 ， 5 6＋x ，x 7 ＋y 8 ，9x＋10 y ，x2 x 中，分式的个数是(B) A．5 B．4 C．3 D．2 2．(陇南中考)若分式x2－4 x 的值为 0，则 x 的值是(A) A．2 或－2 B．2 C．－2 D．0 3．分式4y＋3x 4a ，x2－1 x4－1 ，x2－xy＋y2 x＋y ，a2＋2ab ab－2b2中，最简分式有(C) A．1 个 B．2 个 C．3 个 D．4 个 4．下列各式从左到右的变形中正确的是(A) A. x－1 2 y 1 2 xy ＝2x－y xy B.0.2a＋b a＋2b ＝2a＋b a＋2b C．－x＋1 x－y ＝x－1 x－y D.a＋b a－b ＝a－b a＋b 5．若( 4 a2－4 ＋ 1 2－a )·w＝1，则 w＝(D) A．a＋2(a≠－2) B．－a＋2(a≠2) C．a－2(a≠2) D．－a－2(a≠－2) 6．(成都中考)分式方程x＋1 x ＋ 1 x－2 ＝1 的解是(A) A．x＝1 B．x＝－1 C．x＝3 D．x＝－3 7．若关于 x 的分式方程2x－a x－2 ＝1 2 的解为非负数，则 a 的取值范围是(C) A．a≥1 B．a＞1 C．a≥1 且 a≠4 D．a＞1 且 a≠4 8．(临沂中考)新能源汽车环保节能，越来越受到消费者的喜爱．各种品牌相继投放市 场．一汽贸公司经销某品牌新能源汽车．去年销售总额为 5000 万元，今年 1～5 月份，每辆 车的销售价格比去年降低 1 万元．销售数量与去年一整年的相同．销售总额比去年一整年的 少 20%，今年 1～5 月份每辆车的销售价格是多少万元？设今年 1～5 月份每辆车的销售价格 为 x 万元．根据题意，列方程正确的是(A) A.5000 x＋1 ＝5000（1－20%） x B.5000 x＋1 ＝5000（1＋20%） x C.5000 x－1 ＝5000（1－20%） x D.5000 x－1 ＝5000（1＋20%） x 9．已知1 a ＋ 1 2b ＝3，则代数式2a－5ab＋4b 4ab－3a－6b 的值为(D) A．3 B．－2 C．－1 3 D．－1 2 10．张华在一次数学活动中，利用“在面积一定的矩形中，正方形的周长最短”的结论， 推导出“式子 x＋1 x (x＞0)的最小值是 2”．其推导方法如下：在面积是 1 的矩形中设矩形的 29 一边长为 x，则另一边长是1 x ，矩形的周长是 2(x＋1 x )；当矩形成为正方形时，就有 x＝1 x (x ＞0)，解得 x＝1，这时矩形的周长 2(x＋1 x )＝4 最小，因此 x＋1 x (x＞0)的最小值是 2.模仿 张华的推导，你求得式子x2＋9 x (x＞0)的最小值是(C) A．2 B．1 C．6 D．10 二、填空题(每小题 3 分，共 18 分) 11．已知分式 x－3 x2－5x＋a ，当 x＝2 时，分式无意义，则 a＝6. 12．当 a＝1 2 时，代数式2a2－2 a－1 －2 的值为 1. 13．一个分数的分母比分子大 7，如果此分数的分子加 17，分母减 4，所得的新分数是 原分数的倒数，那么原分数是 3 10 . 14．(达州中考)若关于 x 的分式方程 x x－3 ＋ 3a 3－x ＝2a 无解，则 a 的值为 1 或1 2 . 15．(宿迁中考)为了改善生态环境，防止水土流失，红旗村计划在荒坡上种树 960 棵， 由于青年志愿者支援，实际每天种树的棵数是原计划的 2 倍，结果提前 4 天完成任务，则原 计划每天种树的棵数是 120 棵． 16．(眉山中考)已知关于 x 的分式方程 x x－3 －2＝ k x－3 有一个正数解，则 k 的取值范围 为 k＜6 且 k≠3. 三、解答题(共 72 分) 17．(8 分) 计算： (1)(山西中考)x－2 x－1 · x2－1 x2－4x＋4 － 1 x－2 . 解：原式＝x－2 x－1 ·（x－1）（x＋1） （x－2）2 － 1 x－2 ＝x＋1 x－2 － 1 x－2 ＝ x x－2 (2)(重庆中考)(a－1－4a－1 a＋1 )÷a2－8a＋16 a＋1 . 解：原式＝a2－1－4a＋1 a＋1 · a＋1 （a－4）2＝a（a－4） a＋1 · a＋1 （a－4）2＝ a a－4 18．(8 分)解分式方程： (1)5x－4 x－2 ＝4x＋10 3x－6 －1； 解：无解 30 (2) 3 2x＋1 － 2 2x－1 ＝ x＋1 4x2－1 . 解：去分母得 6x－3－4x－2＝x＋1，解得 x＝6，经检验，x＝6 是分式方程的解 19．(6 分)老师在黑板上书写了一个代数式的正确演算结果，随后用手掌捂住了一部分， 形式如下：( － x2－1 x2－2x＋1 )÷ x x＋1 ＝x＋1 x－1 ，求所捂部分化简后的结果． 解：设所捂部分为 A，则 A＝x＋1 x－1 · x x＋1 ＋ x2－1 x2－2x＋1 ＝ x x－1 ＋x＋1 x－1 ＝2x＋1 x－1 20．(6 分)(泰安中考)先化简，再求值：m2－4m＋4 m－1 ÷( 3 m－1 －m－1)，其中 m＝ 2－2. 解 ： 原 式 ＝ （m－2）2 m－1 ÷ ( 3 m－1 － m2－1 m－1 ) ＝ （m－2）2 m－1 ÷ 4－m2 m－1 ＝ （m－2）2 m－1 · m－1 －（m＋2）（m－2） ＝－m－2 m＋2 ，当 m＝ 2－2 时，原式＝－ 2－2－2 2－2＋2 ＝－ 2－4 2 ＝ －1＋2 2 21．(7 分)小明解方程1 x －x－2 x ＝1 的过程如下： 解：方程两边同乘 x，得 1－(x－2)＝1.① 去括号，得 1－x－2＝1.② 合并同类项，得－x－1＝1.③ 移项，得－x＝2.④ 解得 x＝－2.⑤ ∴原方程的解为 x＝－2.⑥ 请指出他解答过程中的错误，并写出正确的解答过程． 解：小明的解法有三处错误：步骤①去分母有误；步骤②去括号有误；步骤⑥前缺少“检 验”步骤．正确解法是：方程两边同乘 x，得 1－(x－2)＝x.去括号，得 1－x＋2＝x.移项， 得－x－x＝－2－1.合并同类项，得－2x＝－3.两边同除以－2，得 x＝3 2 .经检验，x＝3 2 是原 方程的解．所以原方程的解是 x＝3 2 31 22．(7 分)(徐州中考)徐州至北京的高铁里程约为 700 km，甲、乙两人从徐州出发，分 别乘坐“徐州号”高铁 A 与“复兴号”高铁 B 前往北京．已知 A 车的平均速度比 B 车的平均 速度慢 80 km/h，A 车的行驶时间比 B 车的行驶时间多 40%，两车的行驶时间分别为多少？ 解：设 B 车行驶的时间为 t 小时，则 A 车行驶的时间为 1.4t 小时，根据题意得700 t － 700 1.4t ＝80，解得 t＝2.5，经检验，t＝2.5 是原分式方程的解，且符合题意，∴1.4t＝3.5.答：A 车行驶的时间为 3.5 小时，B 车行驶的时间为 2.5 小时 23．(8 分)先化简：(2x2＋2x x2－1 － x2－x x2－2x＋1 )÷ x x＋1 ，然后解答下列问题： (1)当 x＝3 时，求代数式的值； (2)原代数式的值能等于－1 吗？为什么？ 解：原式＝[ 2x（x＋1） （x＋1）（x－1） －x（x－1） （x－1）2 ]·x＋1 x ＝( 2x x－1 － x x－1 )·x＋1 x ＝ x x－1 ·x＋1 x ＝x＋1 x－1 (1)当 x＝3 时，原式＝2 (2)原代数式的值不能等于－1，理由：如果x＋1 x－1 ＝－1，那么 x＋1＝－x＋1，∴x＝0. 当 x＝0 时，除式 x x＋1 ＝0.∴原代数式的值不能等于－1 24．(10 分)阅读下列材料： 在学习“分式方程及其解法”过程中，老师提出一个问题：若关于 x 的分式方程 a x－1 ＋ 3 1－x ＝1 的解为正数，求 a 的取值范围？ 经过小组交流讨论后，同学们逐渐形成了两种意见： 小明说：解这个关于 x 的分式方程，得到方程的解为 x＝a－2.由题意可得 a－2＞0，所 以 a＞2，问题解决． 小强说：你考虑的不全面．还必须保证 a≠3 才行． 老师说：小强所说完全正确． 请 回 答 ： 小 明 考 虑 问 题 不 全 面 ， 主 要 体 现 在 哪 里 ？ 请 你 简 要 说 明 ： ________________________________________________________________________. 完成下列问题： (1)已知关于 x 的方程2mx－1 x＋2 ＝1 的解为负数，求 m 的取值范围； (2)若关于 x 的分式方程3－2x x－3 ＋2－nx 3－x ＝－1 无解．直接写出 n 的取值范围． 解：小明没有考虑分式的分母不为 0(或分式必须有意义)这个条件 32 (1)解关于 x 的分式方程，得 x＝ 3 2m－1 ，∵方程有解，且解为负数，∴ 2m－1＜0， 3 2m－1 ≠－2，解 得 m＜1 2 且 m≠－1 4 (2)分式方程去分母，得 3－2x＋nx－2＝－x＋3，即(n－1)x＝2，由分式方程无解，得 到 x－3＝0，即 x＝3，代入整式方程得 n＝5 3 ；当 n－1＝0 时，整式方程无解，此时 n＝1， 综上，n＝1 或 n＝5 3 25. (12 分)(德阳中考)为配合“一带一路”国家倡议，某铁路货运集装箱物流园区正 式启动了 2 期扩建工程．一项地基基础加固处理工程由 A、B 两个工程公司承担建设，已知 A 工程公司单独建设完成此项工程需要 180 天，A 工程公司单独施工 45 天后，B 工程公司参 与合作，两工程公司又共同施工 54 天后完成了此项工程． (1)求 B 工程公司单独建设完成此项工程需要多少天？ (2)由于受工程建设工期的限制，物流园区管委会决定将此项工程划分成两部分，要求 两工程公司同时开工，A 工程公司建设其中一部分用了 m 天完成，B 工程公司建设另一部分 用了 n 天完成，其中 m，n 均为正整数，且 m＜46，n＜92，求 A、B 两个工程公司各施工建 设了多少天？ 解：(1)设 B 工程公司单独完成需要 x 天，根据题意得 45× 1 180 ＋54( 1 180 ＋1 x )＝1，解得 x＝120，经检验，x＝120 是分式方程的解，且符合题意，答：B 工程公司单独完成需要 120 天 (2)根据题意得 m× 1 180 ＋n× 1 120 ＝1，整理得 n＝120－2 3 m，∵m＜46，n＜92，∴120－2 3 m ＜92，解得 42＜m＜46，∵m 为正整数，∴m＝43，44，45，又∵120－2 3 m 为正整数，∴m＝ 45，n＝90.答：A，B 两个工程公司分别施工建设了 45 天和 90 天 第六章检测题 (时间：120 分钟 满分：120 分) 一、选择题(每小题 3 分，共 30 分) 1．如图，在平行四边形 ABCD 中，AB＝3，AD＝2，则 CD 等于(B) A．2 B．3 C．4 D．5 33 ,第 1 题图) ,第 3 题图) , 第 5 题图) 2．(宜宾中考)在▱ ABCD 中，若∠BAD 与∠CDA 的角平分线交于点 E，则△AED 的形状是 (B) A．锐角三角形 B．直角三角形 C．钝角三角形 D．不能确定 3．如图，平行四边形 ABCD 的对角线 AC，BD 相交于点 O，下列结论正确的是(A) A．S▱ ABCD＝4S△AOB B．AC＝BD C．AC⊥BD D．▱ ABCD 是轴对称图形 4．(铜仁中考)如果一个多边形的内角和是外角和的 3 倍，则这个多边形的边数是(A) A．8 B．9 C．10 D．11 5．(苏州中考)如图，在△ABC 中，延长 BC 至 D，使得 CD＝1 2 BC，过 AC 中点 E 作 EF∥CD(点 F 位于点 E 右侧)，且 EF＝2CD，连接 DF.若 AB＝8，则 DF 的长为(B) A．3 B．4 C．2 3 D．3 2 6．如图，在平面直角坐标系内，原点 O 恰好在▱ ABCD 对角线的交点处，若点 A 的坐标 为(2，3)，则点 C 的坐标为(C) A．(－3，－2) B．(－2，3) C．(－2，－3) D．(2，－3) ,第 6 题图) ,第 8 题图) ,第 9 题图) 7．(呼和浩特中考)顺次连接平面上 A，B，C，D 四点得到一个四边形，从①AB∥CD；② BC＝AD；③∠A＝∠C；④∠B＝∠D 四个条件中任取其中两个，可以得出“四边形 ABCD 是平 行四边形”这一结论的情况共有(C) A．5 种 B．4 种 C．3 种 D．1 种 8．如图，AD∥BC，∠ABC 的角平分线 BP 与∠BAD 的角平分线 AP 相交于点 P，作 PE⊥AB 于点 E.若 PE＝2，则两平行线 AD 与 BC 间的距离为(A) A．4 B．5 C．6 D．7 9．如图，平行四边形 ABCD 中，AE 平分∠BAD，交 BC 于点 E，且 AB＝AE，延长 AB 与 DE 的延长线交于点 F，下列结论中： ①△ABC≌△ADE；②△ABE 是等边三角形；③AD＝AF；④S△ABE＝S△CDE；⑤S△ABE＝S△CEF.其 中正确的是(C) 34 A．①②③ B．①②④ C．①②⑤ D．①③④ 10．(达州期末)如图，在平行四边形 ABCD 中，AB＝4，∠BAD 的平分线与 BC 的延长线 交于点 E，与 DC 交于点 F，且点 F 为边 DC 的中点，DG⊥AE，垂足为 G，若 DG＝1，则 AE 的 边长为(B) A．2 3 B．4 3 C．4 D．8 二、填空题(每小题 3 分，共 18 分) 11．如图，在▱ ABCD 中，AE＝CG，DH＝BF，连接 E，F，G，H，E，则四边形 EFGH 是平 行四边形． ,第 11 题图) ,第 12 题图) 12．(南京中考)如图，五边形 ABCDE 是正五边形．若 l1∥l2，则∠1－∠2＝72°. 13．(曲靖中考)如图，在△ABC 中，AB＝13，BC＝12，点 D，E 分别是 AB，BC 的中点， 连接 DE，CD，如果 DE＝2.5，那么△ACD 的周长是 18. ,第 13 题图) ,第 14 题图) 14．如图，在平行四边形 ABCD 中，AE⊥BC 于 E，AF⊥CD 于 F，∠EAF＝45°，且 AE＋ AF＝2 2，则平行四边形 ABCD 的周长是 8. 15．如图，分别以 Rt△ABC 的斜边 AB，直角边 AC 为边向外作等边△ABD 和△ACE，F 为 AB 的中点，DE，AB 相交于点 G.若∠BAC＝30°，下列结论：①EF⊥AC；②四边形 ADFE 为平 行四边形；③AD＝4AG；④△DBF≌△EFA.其中正确结论的序号是①②③④. ,第 15 题图) ,第 16 题图) 16．(无锡中考)如图，已知∠XOY＝60°，点 A 在边 OX 上，OA＝2.过点 A 作 AC⊥OY 于 点 C，以 AC 为一边在∠XOY 内作等边三角形 ABC，点 P 是△ABC 围成的区域(包括各边)内的 一点，过点 P 作 PD∥OY 交 OX 于点 D，作 PE∥OX 交 OY 于点 E.设 OD＝a，OE＝b，则 a＋2b 的取值范围是 2≤a＋2b≤5. 点拨：过 P 作 PH⊥OY 交于点 H，∵PD∥OY，PE∥OX，∴四边形 EODP 是平行四边形，∠ 35 HEP＝∠XOY＝60°，∴EP＝OD＝a，Rt△HEP 中，∠EPH＝30°，∴EH＝1 2 EP＝1 2 a，∴a＋2b＝ 2(1 2 a＋b)＝2(EH＋EO)＝2OH，当 P 在 AC 边上时，H 与 C 重合，此时 OH 的最小值为 OC＝1 2 OA ＝1，即 a＋2b 的最小值是 2；当 P 在点 B 时，OH 的最大值是 1＋3 2 ＝5 2 ，即(a＋2b)的最大值 是 5，∴2≤a＋2b≤5 三、解答题(共 72 分) 17．(6 分)(曲靖中考)如图，在平行四边形 ABCD 的边 AB，CD 上截取 AF，CE，使得 AF ＝CE，连接 EF，点 M，N 是线段 EF 上两点，且 EM＝FN，连接 AN, CM.求证：△AFN≌△CEM. 证明：∵四边形 ABCD 是平行四边形，∴CD∥AB，∴∠AFN＝∠CEM，∵FN＝EM，AF＝CE， ∴△AFN≌△CEM(SAS) 18．(6 分)如图，在▱ ABCD 中，对角线 AC 交 BD 于点 O，四边形 AODE 是平行四边形． 求证：四边形 ABOE 是平行四边形． 解：∵在▱ ABCD 中，对角线 AC 交 BD 于点 O，∴OB＝OD.又∵四边形 AODE 是平行四边形， ∴AE∥OD，AE＝OD，∴AE∥OB，AE＝OB，∴四边形 ABOE 是平行四边形 19．(7 分)如图，E，F 是▱ ABCD 对角线 BD 上的两点，给出下列三个条件：①BE＝DF； ②∠AEB＝∠DFC；③AF∥EC.请你从中选择一个适当的条件，使四边形 AECF 是平行四边形， 并证明你的结论． 解：选择条件①，∵在▱ ABCD 中，AC，BD 为对角线，∴OA＝OC，OB＝OD，又 BE＝DF， ∴OE＝OF，∴四边形 AECF 是平行四边形(答案不唯一) 36 20．(8 分)(青海中考)如图，在平行四边形 ABCD 中，E 为 AB 边上的中点，连接 DE 并延 长，交 CB 的延长线于点 F. (1)求证：AD＝BF； (2)若平行四边形 ABCD 的面积为 32，试求四边形 EBCD 的面积． 解：(1)∵E 是 AB 边上的中点，∴AE＝BE.∵AD∥BC，∴∠ADE＝∠F.在△ADE 和△BFE 中，∠ADE＝∠F，∠DEA＝∠FEB，AE＝BE，∴△ADE≌△BFE.∴AD＝BF (2)过点 D 作 DM⊥AB 与 M，则 DM 同时也是平行四边形 ABCD 的高．∴S△AED＝1 2 ×1 2 AB·DM ＝1 4 AB·DM＝1 4 ×32＝8，∴S 四边形 EBCD＝S▱ ABCD－S△ADE＝32－8＝24 21．(8 分)如图，D 是△ABC 的边 AB 上一点，CN∥AB，DN 交 AC 于点 M，若 MA＝MC. (1)求证：CD＝AN； (2)若 AC⊥DN，∠CAN＝30°，MN＝1，求四边形 ADCN 的面积． 解：(1)∵AB∥CN，∴∠BAC＝∠ACN，在△AMD 和△CMN 中，∠DAM＝∠NCM，AM＝CM，∠ AMD＝∠CMN，∴△AMD≌△CMN(ASA)，∴AD＝CN，又∵AD∥CN，∴四边形 ADCN 是平行四边形， ∴CD＝AN (2)∵AC⊥DN，∠CAN＝30°，MN＝1，∴AN＝2MN＝2，则 AM＝ AN2－MN2＝ 22－12＝ 3， ∴S△AMN＝1 2 AM·MN＝1 2 × 3×1＝ 3 2 ，∵四边形 ADCN 是平行四边形，∴S▱ ADCN＝4S△AMN＝2 3 22．(8 分)(巴中中考)如图，在▱ ABCD 中，过 B 点作 BM⊥AC 于点 E，交 CD 于点 M，过 D 点作 DN⊥AC 于点 F，交 AB 于点 N. (1)求证：四边形 BMDN 是平行四边形； (2)已知 AF＝12，EM＝5，求 AN 的长． 37 (1)证明：∵四边形 ABCD 是平行四边形，∴CD∥AB，∵BM⊥AC，DN⊥AC，∴DN∥BM，∴ 四边形 BMDN 是平行四边形 (2)解：∵四边形 BMDN 是平行四边形，∴DM＝BN，∵CD＝AB，CD∥AB，∴ CM＝AN，∠ MCE＝∠NAF，∵∠CEM＝∠AFN＝90°，∴△CEM≌△AFN，∴FN＝EM＝5，在 Rt△AFN 中，AN ＝ AF2＋FN2＝ 52＋122＝13 23．(8 分)如图，在△ABC 中，D 是边 BC 的中点，点 E 在△ABC 内，AE 平分∠BAC，CE ⊥AE，点 F 在边 AB 上，EF∥BC. (1)求证：四边形 BDEF 是平行四边形； (2)线段 BF，AB，AC 之间具有怎样的数量关系？证明你所得到的结论． 解：(1) 延长 CE 交 AB 于点 G，∵AE⊥CE，∴∠AEG＝∠AEC＝90°，在△AEG 和△AEC 中，∠GAE＝∠CAE，AE＝AE，∠AEG＝∠AEC，∴△AEG≌△AEC(ASA)，∴GE＝EC，又∵BD＝ CD，∴DE 为△CGB 的中位线，∴DE∥AB，又∵EF∥BC，∴四边形 BDEF 是平行四边形 (2)∵BF＝1 2 (AB－AC)．理由：∵四边形 BDEF 是平行四边形，∴BF＝DE，∵D，E 分别是 BC，GC 的中点，∴BF＝DE＝1 2 BG，∵△AGE≌△ACE，∴AG＝AC，∴BF＝1 2 (AB－AG)＝1 2 (AB－ AC) 24．(9 分)如图，在 Rt△ABC 中，∠ABC＝90°，DH 垂直平分 AB 交 AC 于点 E，连接 BE， CD，且 CD＝CE. (1)如图 1，求证：四边形 BCDE 是平行四边形；(4 分) (2)如图 2，点 F 在 AB 上，且 BF＝BC，连接 BD，若 BD 平分∠ABC，试判断 DF 与 AC 的 位置关系，并证明你的结论．(5 分) (1)证明：∵DH 垂直平分 AB 交 AC 于点 E，∴AE＝BE，∠AHE＝∠BHE＝90°，∴∠A＝∠ ABE，∠A＋∠AEH＝∠ABE＋∠BEH＝90°，∵∠ABC＝90°，∴∠A＋∠ACB＝90°，∴∠AEH ＝∠ACB＝∠BEH，∵CE＝CD，∴∠D＝∠CED，∵∠AEH＝∠CED，∴∠D＝∠BEH，∠CED＝∠ 38 ACB，∴BE∥CD，BC∥ED，∴四边形 BCDE 是平行四边形 (2)DF⊥AC，证明：∵四边形 BCDE 是平行四边形，∴DE＝BC，∵BC＝BF，∴BF＝DE，∵ BD 平分∠ABC，∠ABC＝90°，∴∠HBD＝45°，∵∠BHD＝90°，∴∠HBD＝∠HDB＝45°， ∴DH＝BH＝AH，∴DH－DE＝BH－BF，∴HE＝HF，在△DHF 和△AHE 中， DH＝AH， ∠DHF＝∠AHE， HF＝HE， ∴△ DHF≌△AHE，∴∠A＝∠FDH，∵∠A＋∠AEH＝90°，∠DEC＝∠AEH，∴∠FDH＋∠DEC＝90°， ∴∠EGD＝180°－90°＝90°，∴DF⊥AC 25. (12 分)如图，在▱ ABCD 中，BD 为对角线，EF 垂直平分 BD 分别交 AD、BC 的于点 E， F，交 BD 于点 O. (1)试说明：BF＝DE； (2)试说明：△ABE≌△CDF； (3)如果在▱ ABCD 中，AB＝5，AD＝10，有两动点 P，Q 分别从 B，D 两点同时出发，沿 △BAE 和△DFC 各边运动一周，即点 P 自 B→A→E→B 停止，点 Q 自 D→F→C→D 停止，点 P 运动的路程是 m，点 Q 运动的路程是 n，当四边形 BPDQ 是平行四边形时，求 m 与 n 满足的数 量关系．(画出示意图) (1)证明：∵四边形 ABCD 是平行四边形，∴AD∥BC，∴∠EDO＝∠FBO，∵EF 垂直平分 BD，∴OB＝OD，在△EOD 和△FOB 中，∵ ∠EOD＝∠FOB， OD＝OB， ∠EDO＝∠FBO， ∴△EOD≌△FOB(ASA)，∴BF＝DE (2)证明：∵△EOD≌△FOB，∴DE＝BF，∵四边形 ABCD 是平行四边形，∴∠A＝∠C，AB ＝CD，AD＝BC，∴AD－DE＝BC－BF，∴AE＝CF，在△ABE 和△CDF 中，∵ AB＝CD， ∠A＝∠C， AE＝CF， ∴△ABE ≌△CDF(SAS) (3)解：∵EF 垂直平分 BD，∴BF＝DF，∵△ABE≌△CDF，∴DF＝BE，AE＝CF，∴△DFC 的周长是 DF＋CF＋CD＝BF＋CF＋CD＝BC＋CD＝15，△ABE 的周长也是 15. ①当 P 在 AB 上，Q 在 CD 上，如图①，∵AB∥CD，∴∠BPO＝∠DQO，∵∠POB＝∠DOQ， OB＝OD，∴△BPO≌△DQO，∴BP＝DQ，∴m＋n＝BP＋DF＋CF＋CQ＝DF＋CF＋CQ＋DQ＝DF＋CF ＋CD＝15 ②当 P 在 AE 上，Q 在 CF 上，如图②，∵AD∥BC，∴∠PEO＝∠QFO，∵△EOD≌△FOB， ∴OE＝OF，∵∠PEO＝∠QFO，∠EOP＝∠FOQ，∴△PEO≌△QFO，∴PE＝QF，∵AE＝CF，∴CQ ＝AP，m＋n＝AB＋AP＋DF＋FQ＝CD＋CQ＋DF＋FQ＝DF＋CF＋CD＝15 ③当 P 在 BE 上，Q 在 DF 上，如图③，∵AD＝BC，AE＝CF，∴DE＝BF，∵DE∥BF，∴四 边形 BEDF 是平行四边形，∴BE＝DF，BE∥DF，∴∠PEO＝∠FQO，∵∠EOP＝∠FOQ，OE＝OF， ∴△PEO≌△QFO，∴PE＝FQ，∴m＋n＝AB＋AE＋PE＋DQ＝CD＋CF＋QF＋DQ＝DF＋CF＋CD＝15 39 期末检测题 (时间：120 分钟 满分：120 分) 一、选择题(每小题 3 分，共 30 分) 1．(德州中考)下列图形中，既是轴对称图形又是中心对称图形的是(B) 2．若分式|x|－1 x＋1 的值为零，则 x 的值是(A) A．1 B．－1 C．±1 D．2 3．(湘西州中考)不等式组 x＞－2 x≤1 的解集在数轴上表示正确的是(C) 4．(贺州中考)下列各式分解因式正确的是(A) A．x2＋6xy＋9y2＝(x＋3y)2 B．2x2－4xy＋9y2＝(2x－3y)2 C．2x2－8y2＝2(x＋4y)(x－4y) D．x(x－y)＋y(y－x)＝(x－y)(x＋y) 5．(甘孜州中考)若 x＝4 是分式方程a－2 x ＝ 1 x－3 的根，则 a 的值为(A) A．6 B．－6 C．4 D．－4 6．如图，在△ABC 中，点 D，E 分别是 AB，AC 的中点，∠A＝50°，∠ADE＝60°，则 ∠C 的度数为(C) A．50° B．60° C．70° D．80° ,第 6 题图) ,第 9 题图) ,第 10 题图) 7．在平面直角坐标系中，已知线段 AB 的两个端点分别是 A(4，－1)，B(1，1)．将线 段 AB 平移后得到线段 A′B′，若点 A′的坐标为(－2，2)，则点 B′的坐标为(A) A．(－5，4) B．(4，3) C．(－1，－2) D．(－2，－1) 8．(淄博中考)“绿水青山就是金山银山”．某工程队承接了 60 万平方米的荒山绿化任 40 务，为了迎接雨季的到来，实际工作时每天的工作效率比原计划提高了 25%，结果提前 30 天完成了这一任务．设实际工作时每天绿化的面积为 x 万平方米，则下面所列方程中正确的 是(C) A.60 x － 60 （1＋25%）x ＝30 B. 60 （1＋25%）x －60 x ＝30 C.60×（1＋25%） x －60 x ＝30 D.60 x －60×（1＋25%） x ＝30 9．一次函数 y1＝kx＋b 与 y2＝x＋a 的图象如图，则下列结论：①当 x＜3 时，y1＞0； ②当 x＜3 时，y2＞0；③当 x＞3 时，y1＜y2，正确的个数是(C) A．0 个 B．1 个 C．2 个 D．3 个 10．如图所示，在四边形 ABCD 中，AB＝CD，对角线 AC，BD 相交于点 O，AE⊥BD 于点 E， CF⊥BD 于点 F，连接 AF，CE，若 DE＝BF，则下列结论：①CF＝AE；②OE＝OF；③四边形 ABCD 是平行四边形；④图中共有四对全等三角形．其中正确结论的个数是(B) A．4 个 B．3 个 C．2 个 D．1 个 二、填空题(每小题 3 分，共 18 分) 11．(宜宾中考)分解因式：2a3b－4a2b2＋2ab3＝2ab(a－b)2. 12．(巴中中考)不等式组 3x≤2x－4， x－1 2 －1＜x＋1的整数解是 x＝－4. 13．(张家界中考)如图，将△ABC 绕点 A 逆时针旋转 150°，得到△ADE，这时点 B，C， D 恰好在同一直线上，则∠B 的度数为 15°. ,第 13 题图) ,第 14 题图) , 第 15 题图) 14．如图，在 Rt△ABC 中，∠B＝90°，AB＝4，BC＝3，AC 的垂直平分线 DE 分别交 AB， AC 于 D，E 两点，则 CD 的长为25 8 . 15．如图，在△ABC 中，AD 是中线，AE 是角平分线，CF⊥AE 于 F，AB＝5，AC＝2，则 DF 的长为 3 2 . 16．如图，平行四边形 ABCD 中，AB＝8 cm，AD＝12 cm，点 P 在 AD 边上以每秒 1 cm 的 速度从点 A 向点 D 运动，点 Q 在 BC 边上，以每秒 4 cm 的速度从点 C 出发，在 CB 间往返运 动，两个点同时出发，当点 P 到达点 D 时停止(同时点 Q 也停止)，在运动以后，以 P，D，Q， B 四点组成平行四边形的次数有 3 次． 三、解答题(共 72 分) 17．(8 分)解方程(或不等式组)： 41 (1) x x－1 －1＝ 3 （x－1）（x＋2） ； 解：去分母得 x(x＋2)－(x－1)(x＋2)＝3，去括号得 x2＋2x－x2－2x＋x＋2＝3，合并 同类项，得 x＝1，检验：当 x＝1 时，x－1＝0，不合题意，应舍去，∴原方程无解 (2) x＋6≤3x＋4， 1＋2x 3 ＞x－1. 解：解方程 x＋6≤3x＋4，得 x≥1，解方程1＋2x 3 >x－1，得 x<4，∴方程的解集为 1≤x ＜4 18．(6 分)(孝感中考)如图，B，E，C，F 在一条直线上，已知 AB∥DE，AC∥DF，BE＝ CF，连接 AD.求证：四边形 ABED 是平行四边形． 证明：∵AB∥DE，AC∥DF，∴∠B＝∠DEF，∠ACB＝∠F.∵BE＝CF，∴BE＋CE＝CF＋CE， ∴BC＝EF.在△ABC 和△DEF 中， ∠B＝∠DEF， BC＝EF， ∠ACB＝∠F， ∴△ABC≌△DEF(ASA)，∴AB＝DE.又∵AB∥ DE，∴四边形 ABED 是平行四边形 19．(6 分)(遵义中考)化简分式( a2－3a a2－6a＋9 ＋ 2 3－a )÷a－2 a2－9 ，并在 2，3，4，5 这四个数 中取一个合适的数作为 a 的值代入求值． 解：原式＝[a（a－3） （a－3）2 － 2 a－3 ]÷ a－2 （a＋3）（a－3） ＝( a a－3 － 2 a－3 )·（a＋3）（a－3） a－2 ＝ a－2 a－3 ·（a＋3）（a－3） a－2 ＝a＋3，∵a≠－3，2，3，∴a＝4 或 a＝5，当 a＝4 时，原式＝7 20．(7 分)(黄冈中考)如图，在▱ ABCD 中，分别以边 BC，CD 作等腰△BCF，△CDE，使 BC＝BF，CD＝DE，∠CBF＝∠CDE，连接 AF，AE. (1)求证：△ABF≌△EDA；(3 分) 42 (2)延长 AB 与 CF 相交于 G.若 AF⊥AE，求证：BF⊥BC.(4 分) (1)证明：∵四边形 ABCD 是平行四边形，∴AB＝CD，AD＝BC，∠ABC＝∠ADC，∵BC＝BF， CD＝DE，∴BF＝AD，AB＝DE，∵∠ADE＋∠ADC＋∠EDC＝360°，∠ABF＋∠ABC＋∠CBF＝360°， ∠EDC＝∠CBF，∴∠ADE＝∠ABF，∴△ABF≌△EDA (2)证明：延长 FB 交 AD 于 H.∵AE⊥AF，∴∠EAF＝90°，∵△ABF≌△EDA，∴∠EAD＝ ∠AFB，∵∠EAD＋∠FAH＝90°，∴∠FAH＋∠AFB＝90°，∴∠AHF＝90°，即 FB⊥AD，∵ AD∥BC，∴FB⊥BC 21．(7 分)△ABC 在平面直角坐标系中的位置如图所示． (1)作△ABC 关于点 C 成中心对称的△A1B1C；(3 分) (2)将△A1B1C 向右平移 4 个单位，作出平移后的△A2B2C2.(4 分) 解：画图略 22．(8 分)(邵阳中考)某公司计划购买 A，B 两种型号的机器人搬运材料．已知 A 型机 器人比 B 型机器人每小时多搬运 30 kg 材料，且 A 型机器人搬运 1000 kg 材料所用的时间与 B 型机器人搬运 800 kg 材料所用的时间相同． (1)求 A，B 两种型号的机器人每小时分别搬运多少材料； (2)该公司计划采购 A，B 两种型号的机器人共 20 台，要求每小时搬运材料不得少于 2800 kg，则至少购进 A 型机器人多少台？ 解：(1)设 B 型机器人每小时搬运 x 千克材料，则 A 型机器人每小时搬运(x＋30)千克材 料，根据题意，得 1000 x＋30 ＝800 x ，解得 x＝120.经检验，x＝120 是所列方程的解．当 x＝120 时，x＋30＝150.答：A 型机器人每小时搬运 150 千克材料，B 型机器人每小时搬运 120 千克 材料 (2)设购进 A 型机器人 a 台，则购进 B 型机器人(20－a)台，根据题意，得 150a＋120(20 43 －a)≥2800，解得 a≥40 3 .∵a 是整数，∴a≥14.答：至少购进 A 型机器人 14 台 23．(8 分)如图，在▱ ABCD 中，AE⊥BC，垂足为点 E，CE＝CD，点 F 为 CE 的中点，点 G 为 CD 上的一点，连接 DF，EG，AG，∠1＝∠2. (1)若 CF＝2，AE＝3，求 BE 的长； (2)求证：∠CEG＝1 2 ∠AGE. 解：(1)∵点 F 为 CE 的中点，∴CE＝CD＝2CF＝4.又∵四边形 ABCD 为平行四边形，∴AB ＝CD＝4.在 Rt△ABE 中，由勾股定理，得 BE＝ AB2－AE2＝ 7 (2)延长 AG，BC 交于点 H.∵∠2＝∠1，∠ECG＝∠DCF，CE＝CD，∴△CEG≌△CDF(AAS)， ∴CG＝CF.∵CD＝CE＝2CF，∴CG＝GD.∵在▱ ABCD 中，AD∥BC，∴∠DAG＝∠CHG，∠ADG＝ ∠HCG.∴△ADG ≌ △ HCG(AAS) ， ∴AG ＝ HG.∵∠AEH ＝ 90° ， ∴EG ＝ AG ＝ HG.∴∠CEG ＝ ∠H.∵∠AGE＝∠CEG＋∠H，∴∠AGE＝2∠CEG，即∠CEG＝1 2 ∠AGE 24．(10 分)【发现】 任意五个连续整数的平方和是 5 的倍数． 【验证】 (1)(－1)2＋02＋12＋22＋32 的结果是 5 的几倍？(3 分) (2)设五个连续整数的中间一个为 n，写出它们的平方和，并说明是 5 的倍数．(3 分) 【延伸】 任意三个连续整数的平方和被 3 除的余数是几呢？请写出理由．(4 分) 解：【验证】 (1)(－1)2＋02＋12＋22＋32＝1＋0＋1＋4＋9＝15，15÷5＝3，即(－1)2 ＋02＋12＋22＋32 的结果是 5 的 3 倍 (2)设五个连续整数的中间一个为 n，则其余的 4 个整数分别是 n－2，n－1，n＋1，n ＋2，它们的平方和为(n－2)2＋(n－1)2＋n2＋(n＋1)2＋(n＋2)2＝n2－4n＋4＋n2－2n＋1＋n2 ＋n2＋2n＋1＋n2＋4n＋4＝5n2＋10＝5(n2＋2)，又∵n 是整数，∴n2＋2 是整数，∴五个连续 整数的平方和是 5 的倍数 【延伸】 设三个连续整数的中间一个为 n，则其余的 2 个整数是 n－1，n＋1，它们的 平方和为(n－1)2＋n2＋(n＋1)2＝n2－2n＋1＋n2＋n2＋2n＋1＝3n2＋2，∵n 是整数，∴n2 是整 数，∴任意三个连续整数的平方和被 3 除的余数是 2 25. (12 分)如图①，点 A 是线段 BC 上一点，△ABD 和△ACE 都是等边三角形． (1)连接 BE，CD，求证：BE＝CD；(4 分) (2)如图②，将△ABD 绕点 A 顺时针旋转得到△AB′D′. ①当旋转角为 度时，边 AD′落在边 AE 上；(3 分) ②在①的条件下，延长 DD′交 CE 于点 P，连接 BD′，CD′，当线段 AB，AC 满足什么 44 数量关系时，△BDD′与△CPD′全等？并给予证明．(5 分) 解：(1)∵△ACE 和△ABD 都是等边三角形，∴AB＝AD，AE＝AC，∠BAD＝∠EAC＝60°， ∴∠BAD＋∠DAE＝∠EAC＋∠DAE，即∠BAE＝∠DAC，∴△BAE≌△DAC(SAS)，∴BE＝CD (2) ①60 ②当 AC＝2AB 时，△BDD′与△CPD′全等．证明：∵由旋转可知△ABD≌△AB′D′， ∵△ABD 为等边三角形，∴△AB′D′也为等边三角形，且它们的边长相等，∴AB＝BD＝DD′ ＝AD′，∠BDA＝∠D′DA＝60°，∴∠BDD′＝120°，∴∠DBD′＋∠DD′B＝60°，∵BD ＝DD′，∴∠DBD′＝∠DD′B＝1 2 ×60°＝30°，∵AC＝2AB，且 AB＝AD′，∴AC＝2AD′， 又∵△ACE 为等边三角形，∴AC＝AE，∴AE＝2AD′，∴D′为 AE 的中点，∴D′E＝AD′＝ DD′，∵△ADD′为等边三角形，∴∠AD′D＝60°，∴∠PD′E＝∠AD′D＝60°，又∵∠E ＝60°，∴∠EPD′＝60°，∴△PD′E 为等边三角形，∴PD′＝D′E，∴PD′＝DD′，∵ ∠EPD′＝60°，∴∠D′PC＝120°，∴∠BDD′＝∠CPD′＝120°，∵△ACE 为等边三角形， D′为 AE 的中点，∴∠PCD′＝1 2 ∠ACE＝30°，在△BDD′和△CPD′中，∠DBD′＝∠PCD′ ＝30°，∠BDD′＝∠CPD′＝120°，DD′＝PD′，∴△BDD′≌△CPD′(AAS)