华师版数学八年级上册同步练习课件-第13章-13三角形全等的判定 24页

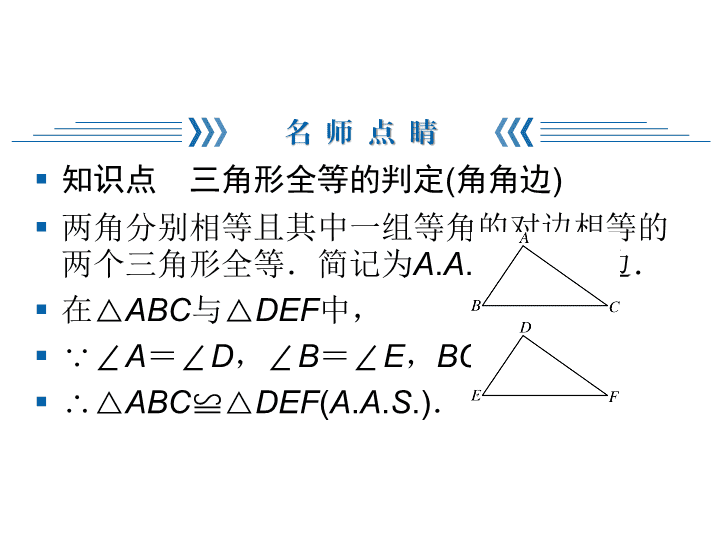
第13章　全等三角形 4　角边角(2)(第四课时) § 知识点　三角形全等的判定(角角边) § 两角分别相等且其中一组等角的对边相等的 两个三角形全等．简记为A.A.S.或角角边． § 在△ABC与△DEF中， § ∵∠A＝∠D，∠B＝∠E，BC＝EF， § ∴△ABC≌ △DEF(A.A.S.)． 2 § 注意：(1)要证两条线段相等或两个角相等， 我们可以证明它们所在的两个三角形全等， 从而利用全等三角形的性质得到结论． § (2)由三角形的内角和定理知，只要两个三角 形的两个角分别相等，则其第三个角也相等， 所以两角及一边分别相等的两个三角形一定 全等．即无论这一边是“对边”还是“夹 边”，只要相等即可判定两个三角形全等． 3 § 【典例】如图，点B、E、C、F在同一直线 上，AB＝DE，∠A＝∠D，AC∥DF.求证： △ABC≌ △DEF. § 分析：首先根据AC∥DF可得∠ACB＝∠F， 再由A.A.S.即可证明△ABC≌△DEF. 4 § 点评：无论是“角边角”还是“角角边”， 都要找出两组角和一组边相等． 5 § 1．在△ABC和△A′B′C′中，已知AB＝A′B′， ∠A＝∠A′，∠C＝∠C′，直接判定 △ABC≌ △A′B′C′的根据是 (　　) § A．S.S.S. B．A.S.A. § C．A.A.S. D．S.A.S. § 2．根据下列已知条件，能画出唯一△ABC 的是 (　　) § A．AB＝5，BC＝3，AC＝8 B．AB＝4， BC＝3，∠A＝30° § C．∠C＝90°，AB＝6 D．∠A＝60°， ∠B＝45°，AB＝4 6 C　 D　 § 3．如图，在△ABC中，∠B＝90°，AB＝3， BC＝4，AC＝5，∠1＝∠2，则点C到直线 AE的距离是 (　　) § A．3 § B．4 § C．4.5 § D．5 7 B　 § 4．【2018·贵州黔西南中考】如图，a、b、 c为三角形的边长，则甲、乙、丙三个三角形 和左侧△ABC全等的是 (　　) § A．甲和乙 B．乙和丙 § C．甲和丙 D．只有丙 8 B　 § 5．【2018·黑龙江牡丹江中考】如图，AC ＝BC，请你添加一对边或一对角相等的条件， 使AD＝BE.你所添加的条件是 ___________________________________ _________________. 9 ∠A＝∠B或∠ADC＝∠BEC或CE＝CD　 (答案不唯一)　 § 6．如图，直线a经过正方形ABCD的顶点A， 分别过正方形的顶点B、D作BF⊥a于点F， DE⊥a于点E，若DE＝8，BF＝5，则EF的 长为______. 10 13　 § 7．如图，已知AB＝CD，∠B＝∠C，AC和 BD相交于点O. § 求证：△AOB≌ △DOC. 11 § 8．【2018·四川宜宾中考】如图，已知∠1 ＝∠2，∠B＝∠D，求证：CB＝CD. 12 § 9．如图，已知∠DCE＝90°，∠DAC＝ 90°，BE⊥AC于点B，且DC＝EC，若BE ＝7，AB＝3，则AD的长为 (　　) § A．3 § B．5 § C．4 § D．不确定 13 C　 14 B　 § 11．如图，Rt△ABC中，AB⊥AC， AD⊥BC，BE平分∠ABC，交AD于点E， EF∥AC，下列结论一定成立的是 (　　) § A．AB＝BF § B．AE＝ED § C．AD＝DC § D．∠ABE＝∠DFE 15 A　 § 12．如图，在△ABC中，AD⊥BC于点D， BE⊥AC于点E，AD与BE相交于点F，若BF ＝AC，∠CAD＝25°，则∠ABE的度数为 (　　) § A．30° § B．15° § C．25° § D．20° 16 D　 § 13．如图，△ABC中，∠ACB＝90°，AC ＝BC＝5，BE⊥CE于点E，AD⊥CE于点D， AD＝4，BE＝3，则DE＝_____. 17 1　 § 14．如图，∠E＝∠F＝90°，∠B＝∠C， AE＝AF，给出下列结论：①∠1＝∠2； ②CD＝DN；③△ACN≌ △ABM；④BE＝ CF.其中正确的结论有__________. 18 ①③④　 § 15．如图，在四边形ABCD中，AB＝BC， ∠ABC＝∠CDA＝90°，BE⊥AD于点E， 且四边形ABCD的面积为12，则BE的长为 _______. 19 § 16．如图，在△ABC中，D是边AB上一点， E是边AC的中点，作CF∥AB交DE的延长线 于点F. § (1)证明：△ADE≌ △CFE； § (2)若AB＝AC，CE＝5，CF＝7，求DB. 20 21 § 17．如图1，在△ABC中，∠ACB＝90°， AC＝BC，过点C在△ABC外作直线MN， AM⊥MN于点M，BN⊥MN于点N. § (1)求证：MN＝AM＋BN； § (2)若过点C在△ABC内作直线MN， AM⊥MN于点M，BN⊥MN于点N，则AM、 BN与MN之间有什么关系？请说明理由． 22 23 24