正方形数学教案 3页

‎ 正方形 教学目标 ‎1、掌握正方形的概念﹑性质以及正方形的判定条件。‎ ‎2、 经历探索正方形概念﹑性质以及正方形判定条件的过程，在活动中发展学生的探究意识和有条理的表达能力。‎ ‎3 、在对正方形特殊性质的探索过程中，理解特殊与一般的关系，领会特殊事物的本质属性与其特殊性质的关系。‎ 教学重点 掌握正方形的概念﹑性质以及正方形的判定条件。‎ 教学难点 掌握正方形的概念﹑性质以及正方形的判定条件。‎ 教学过程 复习导入 ‎1.回顾平行四边形、矩形、菱形的形成过程。2.正方形是由哪个图形旋转得到的？‎ 探索活动 ‎1．思考：你能类比矩形、菱形的概念给正方形下个定义吗?‎ 正方形形的概念：____________并且____________ 的 _________ 是正方形。‎ ‎2.探究：（1）比较平行四边形、矩形、菱形、正方形之间的关系.‎ ‎（2）探索正方形的性质 ‎ 图形 性质 正方形 对称性 边 角 对角线 ‎（3）探索正方形的判定 活动一：如何从长方形木板中截出最大的正方形木板?‎ 活动二：怎样使菱形的衣帽架变成正方形的衣帽架? 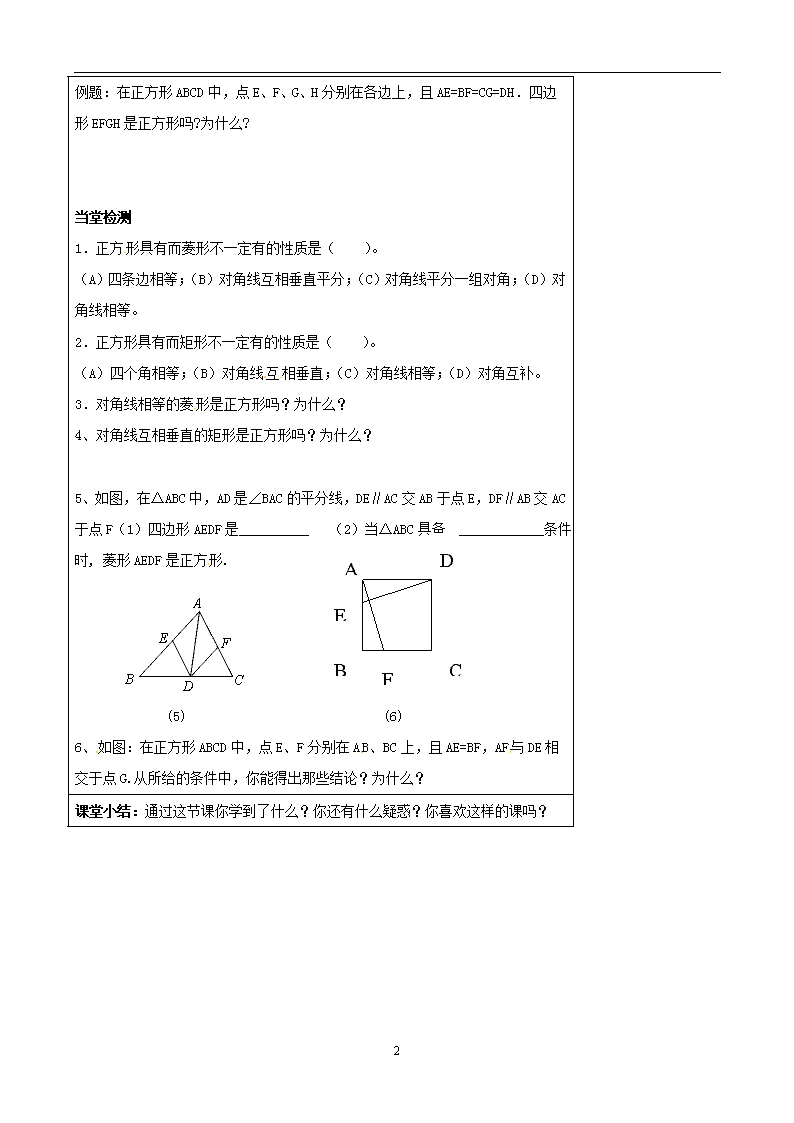‎ ‎（4）总结正方形的判定条件 例题教学 3‎ 例题：在正方形ABCD中，点E、F、G、H分别在各边上，且AE=BF=CG=DH．四边形EFGH是正方形吗?为什么? ‎ 当堂检测 ‎1．正方形具有而菱形不一定有的性质是（ ）。‎ ‎（A）四条边相等；（B）对角线互相垂直平分；（C）对角线平分一组对角；（D）对角线相等。‎ ‎2．正方形具有而矩形不一定有的性质是（ ）。‎ ‎（A）四个角相等；（B）对角线互相垂直；（C）对角线相等；（D）对角互补。‎ ‎3．对角线相等的菱形是正方形吗？为什么？‎ ‎4、对角线互相垂直的矩形是正方形吗？为什么？‎ A C B D F E ‎5、如图，在△ABC中，AD是∠BAC的平分线，DE∥AC交AB于点E，DF∥AB交AC于点F（1）四边形AEDF是__________ （2）当△ABC具备______________条件时, 菱形AEDF是正方形. ‎ ‎ (5) (6)‎ ‎6、如图：在正方形ABCD中，点E、F分别在AB、BC上，且AE=BF，AF与DE相交于点G.从所给的条件中，你能得出那些结论？为什么？‎ 课堂小结：通过这节课你学到了什么？你还有什么疑惑？你喜欢这样的课吗？‎ 3‎ 课外检测 ‎1、如图，等边三角形EBC在正方形ABCD内，连接DE，则∠CDE＝ °。‎ ‎2、在正方形ABCD中，AC、BD交于点O，OE⊥BC于点E，若OE＝2cm，则正方形ABCD的面积为 cm2。‎ ‎3．如图，点E在正方形ABCD的边BC的延长线上，如果BE=BD，那么 ‎（第1题）‎ ‎（第3题）‎ ‎（第4题）‎ ‎∠E＝_____°‎ ‎4、如图，E是在正方形ABCD的延长线上一点，且CE=AC，则∠E= 。‎ ‎5、正方形ABCD中，AB=1，点P是对角线AC上的一点，分别以AP、PC为对角线作正方形，则两个小正方形的周长的和是_________。‎ ‎6、已知：如图，在正方形ABCD中，G是CD上一点，延长BC到E，使CE＝CG，连接BG并延长交DE于F．‎ ‎（1）求证：△BCG≌△DCE； ‎ ‎（2）将△DCE绕点D顺时针旋转90°得到△DAE′，判断四边形E′BGD是什么特殊四边形？并说明理由。‎ 教后反思 3‎