矩形的性质学案 6页

‎ ‎ ‎3.5矩形的性质 班级 姓名 学号 ‎ 学习目标 知识与技能：探索并掌握矩形的有关性质，领会矩形的内涵．‎ 过程与方法：经历探索矩形有关性质的过程，在直观操作活动中学会简单说理，发展初步的合情推理能力和主动探究习惯，逐步掌握说理的基本方法．‎ ‎ 情感态度与价值观：形成良好的几何感知，体会几何学的逻辑内涵，发展思维．‎ 学习难点 理解和掌握矩形的性质,发展合情推理能力和主动探究习惯．‎ 教学过程 ‎ ‎ 一、回顾 ‎ 1．平行四边形有哪些特征？‎ ‎ 2．有几种方法可以识别四边形是平行四边形？‎ ‎ 3．平行四边形是中心对称图形吗？它的对称中心是什么样的点？平行四边形是轴对称图形吗？如果是，它的对称轴是怎样的直线？如果不是，请说明理由．‎ ‎ 二、创设问题情境，引入新课 ‎ 1．教师出示教具：“一个活动的平行四边形木框”，用两根橡皮筋分别套在相对的两个顶点上．‎ 拉动一对不相邻的顶点A、C，立即改变平行四边形的形状，如图所示．‎ ‎ 学生思考如下问题：‎ ‎ （1）无论∠α如何变化，四边形ABCD还是平行四边形吗？‎ ‎ （2）随着∠α的变化，两条对角线长度有没有变化？‎ ‎ 学生凭直觉可以很快地回答上述问题．‎ ‎ 随着∠α由锐角变成钝角时，过∠α顶角的对角线由长变短，而另一条对角线由短变长．‎ ‎ 当∠α是锐角时，学生可以用刻度尺量出两条对角线的长度，你可判别它们数量之间的关系吗？‎ ‎ 当∠α是钝角时，学生也可以用同样办法，得到两对角线的数量关系．‎ ‎ （3）当∠α为直角时，这个时候平行四边形就变成一个特殊的平行四边形──矩形．‎ ‎ 这就是你们以前学过的长方形．‎ ‎ 教师根据学生的回答．板书：矩形．‎ ‎ 这就是我们今天着手研究的一个课题．‎ 6‎ ‎ ‎ ‎ （4）那怎样的平行四边形是矩形呢？‎ ‎ 2．同学回答，老师板书：有一个内角为直角的平行四边形是矩形？‎ ‎ 如果人家问怎样的四边形是矩形呢？‎ ‎ 那就要说四个内角都是直角（或三个内角是直角）的四边形是矩形． 大家想一想矩形是平行四边形吗？９是）‎ ‎ 那么矩形就具有平行四边形的一切特征．‎ ‎ 即矩形是中心对称图形；对边分别平行；两组对边分别相等；两组对角分别相等；对角线互相平分．‎ ‎ 3．矩形除了以上特征外，还有它的特有的性质吗？‎ ‎ 学生思考以下问题：‎ ‎ （1）上面的活动架当∠α为直角时，它们的对角线有何关系？‎ ‎ （2）矩形是轴对称图形吗？如果是，它的对称轴是怎样的直线？如果不是请说明理由．‎ ‎ （3）说出日常生活中的矩形图象．‎ ‎ 4．让我们一起来归纳矩形的性质，并板书：‎ ‎ （1）矩形具有平行四边形的一切性质．‎ ‎ （2）矩形是轴对称图形．‎ ‎ （3）矩形的对角线相等．‎ ‎ （4）矩形的四个角都是直角．‎ ‎ 三、讲解例题 例1 矩形ABCD被两条对角线分成四个小三角形，如果四个小三角形周长的和为86cm，对角线长为13cm，那么矩形的周长是多少？‎ ‎ 学生思考交流后．‎ ‎ 师生共同分析：要求矩形ABCD的周长，就必要求出AB、BC、CD、AD的长度，由于AB=DC，AD=BC，那么只要求出AB、BC或CD、AD即可．‎ ‎ 而矩形的对角线相等且互相平分，又对角线AC=13cm，所以OA=OB=OC=OD=cm=6.5cm．‎ ‎ 这样通过四个小三角形的周长和得到答案．‎ ‎ 点拨：上面从求AB、BC、CD、AD的长度来考虑是一种常见的方法，这里是很难实现的与上次讲述的从整体考虑也是一种好方法，即求AB+BC+CD+AD的值，本题应该从这方面入手．‎ ‎ 解：因为△AOB、△BOC、△COD、△AOD的周长的和为86cm，四边形ABCD是矩形，‎ ‎ 所以AC=BD=13cm，AO=OB=OC=OD 6‎ ‎ ‎ ‎ 则AO+OB+AB+BO+OC+BC+CO+CD+OD+AO+OD+AD=86（cm）‎ ‎ 即AB+BC+CD+AD=86-2AC-2BD=86-2×13-2×13=34（cm）‎ ‎ 所以矩形ABCD的周长为34cm．‎ 练一练 ‎1.矩形的定义中有两个条件:一是____________,二是_________________。‎ ‎2.有一个角是直角的四边形是矩形。（ ）‎ ‎3.矩形的对角线互相平分。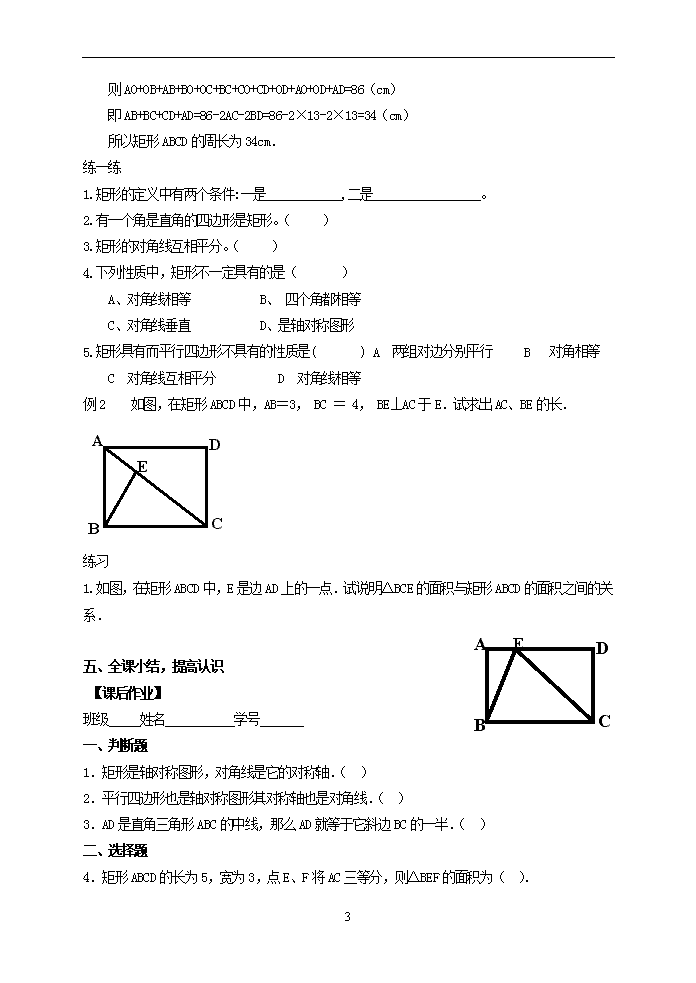（ ） ‎ ‎4.下列性质中，矩形不一定具有的是（ ）‎ ‎ A、对角线相等 B、 四个角都相等 ‎ C、对角线垂直 D、是轴对称图形 ‎ ‎5.矩形具有而平行四边形不具有的性质是( ) A 两组对边分别平行 B 对角相等 ‎ C 对角线互相平分 D 对角线相等 例2 如图，在矩形ABCD中，AB＝3， BC ＝ 4， BE⊥AC于E．试求出AC、BE的长．‎ A B D C E 练习 ‎1. 如图，在矩形ABCD中，E是边AD上的一点．试说明△BCE的面积与矩形ABCD的面积之间的关系．‎ E A B D C ‎ 五、全课小结，提高认识 ‎ 【课后作业】‎ 班级 姓名 学号 ‎ 一、判断题 ‎1．矩形是轴对称图形，对角线是它的对称轴．（ ）‎ ‎2．平行四边形也是轴对称图形其对称轴也是对角线．（ ）‎ ‎3．AD是直角三角形ABC的中线，那么AD就等于它斜边BC的一半．（ ）‎ 二、选择题 ‎4．矩形ABCD的长为5，宽为3，点E、F将AC三等分，则△BEF的面积为（ ）．‎ 6‎ ‎ ‎ ‎ A． D．5‎ ‎5．已知矩形ABCD的AB=2BC，在CD上取点E，使AE=EB，那么∠EBC等于（ ）．‎ ‎ A．60° B．45° C．30° D．15°‎ ‎6．已知E、F分别是矩形ABCD的对边BC和AD上的点，且BE=BC，AF=AD，连结AC、EF，那么（ ）．‎ ‎ A．AC平分EF，但EF不平分AC B．AC与EF互相平分 ‎ C．EF平分AC，但AC不平分EF D．AC与EF不会互相平分 ‎7．如果矩形ABCD的对角线AC和BD所成的锐角是60°，那么（ ）．‎ ‎ A．AC+BD=AB+BC+CD+DA B．BD=2AB C．AC+BD=AB+BC D．以上都不对 ‎8．一个矩形和一个平行四边形的边分别相等，若矩形面积为这个平行四边形的面积的2倍，则平行四边形的锐角的度数为（ ）．‎ ‎ A．15° B．30° C．45° D．60°‎ ‎9．过四边形各顶点分别作对角线的平行线，若这四条平行线围成一个矩形，则原四边形一定是（ ）．‎ ‎ A．对角线相等的四边形 B．对角线垂直的四边形 ‎ C．对角线互相平分且相等的四边形 D．对角线互相垂直且平分的四边形 ‎10．E为矩形ABCD的边CD上的一点，AB=AE=4，BC=2，则∠BEC是（ ）．‎ ‎ A．15° B．30° C．60° D．75°‎ ‎11．如图1所示，矩形ABCD的对角线交于O，AE⊥BD于E，∠1：∠2=2：1，则∠1的度数为（ ）．‎ A．22．5° B．45° C．30° D．60°‎ ‎ ‎ ‎ (1) (2) (3) (4)‎ ‎12．下列叙述错误的是（ ）．‎ ‎ A．平行四边形的对角线互相平分 B．对角线互相平分的四边形是平行四边形 ‎ C．矩形的对角线相等 D．对角线相等的四边形是矩形 ‎13．下列性质矩形不一定具备的是（ ）．‎ 6‎ ‎ ‎ ‎ A．对角线相等 B．四个内角都相等 C．对角线互相平分D．对角线互相垂直 三、填空题 ‎14．如图2所示，O为矩形ABCD的对角线交点，DF平分∠ADC交AC于E，BC于F，∠BDF=15°，则∠COF=______．‎ ‎15．矩形ABCD中，AB=8，BC=6，E、F、G是AD的四等分点，则△BEF的面积是_____．‎ ‎16．若矩形两邻边之比为3：4，周长为28cm，则它的边长为______．‎ ‎17．已知矩形的对角线与较长边所夹的角等于30°，那么较短边与两对角线所围成的三角形是________三角形．‎ ‎18．矩形ABCD的周长为40cm，O是它的对角线交点，△AOB比△AOD周长多4cm，则它的各边长之比为________．‎ ‎19．如图3所示，矩形ABCD中，AE⊥BD于E，∠DAE=3∠BAE，则∠BAE=_____，∠EAD=_____，∠EAC=_____．‎ ‎20．矩形ABCD中，M为AD的中点，MB⊥MC，矩形的周长为24，则AB=_____，BC=_______．‎ ‎21．O为矩形ABCD的对角线交点，∠AOB=2∠BOC，对角线AC=12，则CB=_______．‎ ‎22．如图4所示，在矩形ABCD中，AB=2BC，在CD上取点E，使AE=AB，则∠EAB=_____，∠BEC=________．‎ ‎23．M为矩形ABCD的BC上一点，DN⊥AM于N，AB=3，BC=7，AM=5，则DN=______．‎ 四、解答题 ‎24．如图所示，矩形ABCD中，AC、BD相交于O，AE平分∠BAD交BC于E，若∠CAE=15°的度数，求∠BOE的度数．‎ ‎25．如图所示，矩形ABCD中，对角线AC、BD交于O点，CE⊥BD于E，OF⊥AB于F，BE：DE=1：3，OF=2cm，求AC的长．‎ 6‎ ‎ ‎ ‎26．如图所示，矩形ABCD中，长为7，宽为6，点E、F将BD三等分，求△AEF的面积．‎ ‎27．如图所示，矩形ABCD沿AE折叠，使点D落在BC边长的点F处，如果∠BAE=60°，求∠DAE的度数．‎ 6‎