苏教版数学八年级上册教案1-3探索三角形全等的条件（4） 3页

- 1 - 1.3 探索三角形全等的条件（4） 教学目标 【知识与能力】 1．掌握“边边边（SSS）”的内容并会熟练应用。 2．尺规作图画角平分线，并能说出其作法正确的理由。 【过程与方法】 了解三角形的稳定性及其在生产生活中的广泛应用。 【情感态度价值观】 引导学生经历观察、只做、画图、猜想等活动，并鼓励学生充分的交流讨论、质疑说明、归 纳结论，协调发展学生的合情推理与演绎推理能力. 教学重难点 【教学重点】 掌握三角形全等的“边边边”条件. 【教学难点】 正确运用“边边边”条件判定三角形全等，解决实际问题. 课前准备 无 教学过程 一、知识回顾 三角形全等的判定方法。 二、创设情境 做一做：按下列画法,用圆规和刻度尺画一个三角形：⑴画线段 AB=4cm．⑵分别以点 A、B 为圆心，3cm、2cm 的长为半径画弧，两弧相交于点 C．⑶连接 AC、BC．你所画的三角形 与同学所画的三角形能够重合吗? 三、新知探索 1．用直尺和圆规作△ABC，使 AB=c，AC=b，BC=a。 点拨：理解作图语言的叙述。（课本 P23 页） 2．三角形全等的条件 4：三边分别（对应）相等的两个三角形全等，简写为“边边边”或 “SSS”。 几何语言：如图，在△ABC 和△DEF 中， AB=∠DE BC=EF AC=DF ∴△ABC≌△DEF（SSS）。 3．如果一个三角形三边的长度确定，那么这个三角形的形状和大小就完全确定．三角形的 这种性质叫做三角形的稳定性。 说明：1．四边形不具备稳定性（结合教具）。 问题：（1）四边形木框至少要钉 根木条可使其稳固？五边形、六边形呢？ c b a - 2 - （2）怎样使一个四边形的形状、大小唯一确定？——感受将四边形转化为三角形。 2．三角形稳定性的实例——工地上的塔吊、空调架、三轮车等。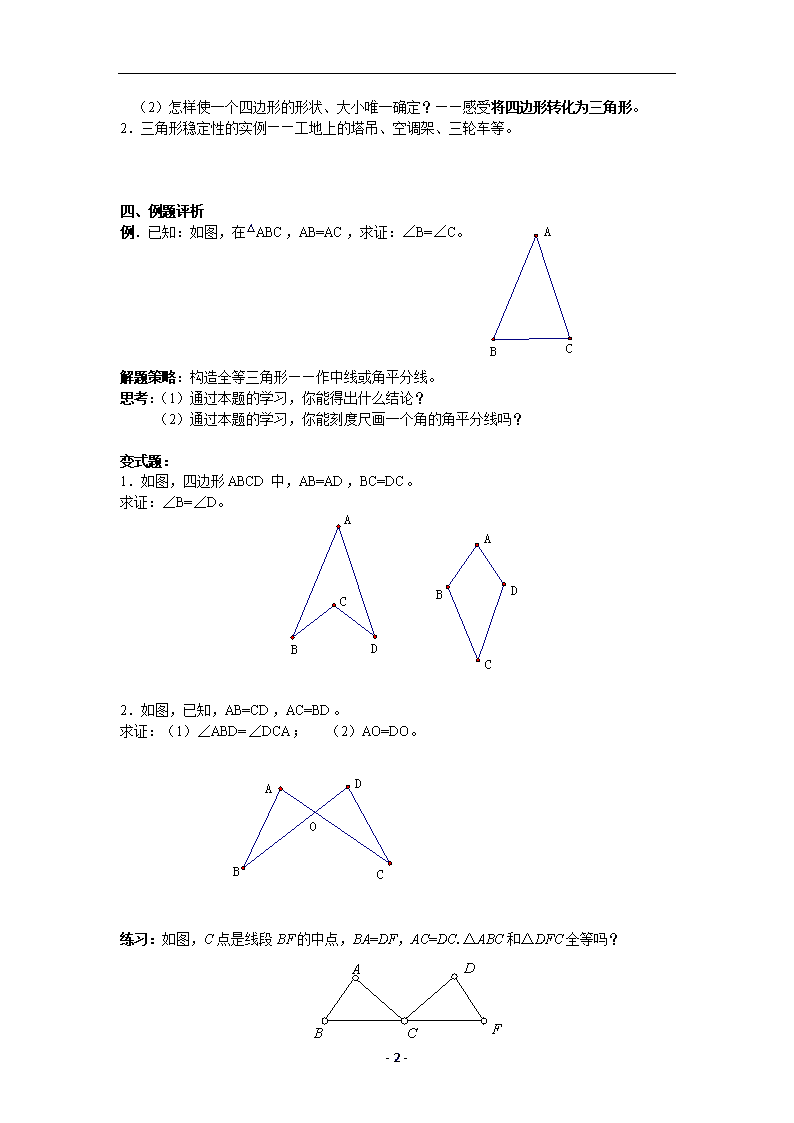 四、例题评析 例．已知：如图，在△ABC，AB=AC，求证：∠B=∠C。 解题策略：构造全等三角形——作中线或角平分线。 思考：（1）通过本题的学习，你能得出什么结论？ （2）通过本题的学习，你能刻度尺画一个角的角平分线吗？ 变式题： 1．如图，四边形 ABCD 中，AB=AD，BC=DC。 求证：∠B=∠D。 2．如图，已知，AB=CD，AC=BD。 求证：（1）∠ABD=∠DCA； （2）AO=DO。 练习：如图，C 点是线段 BF 的中点，BA=DF，AC=DC.△ABC 和△DFC 全等吗？ B F C A D CB A D C B A D C B A O D CB A - 3 - 变形 1：若将这两个三角形，向内侧移动形成下图，若 AB=DF，AC=DE，BE=CF.你能找到 一对全等三角形吗？说明你的理由. 变形 2：若将第一题中的两个三角形拉开，再翻折形成下图，如图，点 B、C、E、F 在同一 条直线上，AB=DF，BC=EF，AC=DE.那么∠B 与∠F 相等吗？为什么？ 五、课堂小结与反思 1．判断三角形全等的方法有：定义、SAS、ASA、AAS、SSS。除定义外，每种判定方法都 要有“三对元素”对应相等，且至少有一条边。因此，在判定两个三角形全等时，应先找对 应的“边”。 2．判定两个三角形全等的方法中，不存在边边角、角角边。 反例如右图。 3．证线段、角相等时，常借助证两个三角形全等。有时需要添加辅助线。 B F A C D E ED CB A DCB A