2019学年八年级数学下册 知识点总结 3页

知识点总结 平移与旋转 旋转 1. 旋转的定义：‎ ‎ 在平面内，将一个图形绕一个定点沿某个方向转动一个角度，这样的图形运动叫做旋转。‎ 2. 旋转的性质：‎ ‎ 旋转后得到的图形与原图形之间有：对应点到旋转中心的距离相等，旋转角相等。‎ 中心对称 1. 中心对称的定义：‎ ‎ 如果一个图形绕某一点旋转180度后能与另一个图形重合，那么这两个图形叫做中心对称。‎ 2. 中心对称图形的定义：‎ ‎ 如果一个图形绕一点旋转180度后能与自身重合，这个图形叫做中心对称图形。‎ 3. 中心对称的性质：‎ ‎ 在中心对称的两个图形中，连结对称点的线段都经过对称中心，并且被对称中心平分。‎ 轴对称 1. 轴对称的定义：‎ ‎ 如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对 称图形，这条直线叫做对称轴。‎ 2. 轴对称图形的性质：‎ ‎ ①角的平分线上的点到这个角的两边的距离相等。 ‎ ‎ ②线段垂直平分线上的点到这条线段两个端点的距离相等。 ‎ ‎ ③等腰三角形的“三线合一”。‎ ‎3.轴对称的性质：对应点所连的线段被对称轴垂直平分，对应线段/对应角相等。‎ 图形变换 图形变换的定义：图形的平移、旋转、和轴对称统称为图形变换。‎ 函数及其相关概念 ‎ ‎ ‎ ‎1、变量与常量 ‎ 在某一变化过程中，可以取不同数值的量叫做变量，数值保持不变的量叫做常量。‎ 一般地，在某一变化过程中有两个变量x与y，如果对于x的每一个值，y都有唯一确定的值与它对应，那么就说x是自变量，y是x的函数。‎ ‎2、函数解析式 用来表示函数关系的数学式子叫做函数解析式或函数关系式。‎ 使函数有意义的自变量的取值的全体，叫做自变量的取值范围。‎ ‎3、函数的三种表示法及其优缺点 ‎（1）解析法 两个变量间的函数关系，有时可以用一个含有这两个变量及数字运算符号的等式表示，这种表示法叫做解析法。‎ ‎（2）列表法 把自变量x的一系列值和函数y的对应值列成一个表来表示函数关系，这种表示法叫做列表法。‎ 3‎ ‎（3）图像法 用图像表示函数关系的方法叫做图像法。‎ ‎4、由函数解析式画其图像的一般步骤 ‎（1）列表：列表给出自变量与函数的一些对应值 ‎（2）描点：以表中每对对应值为坐标，在坐标平面内描出相应的点 ‎（3）连线：按照自变量由小到大的顺序，把所描各点用平滑的曲线连接起来。‎ 正比例函数和一次函数 ‎ ‎1、正比例函数和一次函数的概念 一般地，如果（k，b是常数，k0），那么y叫做x的一次函数。‎ 特别地，当一次函数中的b为0时，（k为常数，k0）。这时，y叫做x的正比例函数。‎ ‎2、一次函数的图像 所有一次函数的图像都是一条直线 ‎3、一次函数、正比例函数图像的主要特征：‎ 一次函数的图像是经过点（0，b）的直线；正比例函数的图像是经过原点（0，0）的直线。（如下图）‎ ‎4. 正比例函数的性质 一般地，正比例函数有下列性质：‎ ‎（1）当k>0时，图像经过第一、三象限，y随x的增大而增大；‎ ‎（2）当k<0时，图像经过第二、四象限，y随x的增大而减小。‎ ‎5、一次函数的性质 一般地，一次函数有下列性质：‎ ‎（1）当k>0时，y随x的增大而增大 ‎（2）当k<0时，y随x的增大而减小 ‎6、正比例函数和一次函数解析式的确定 确定一个正比例函数，就是要确定正比例函数定义式（k0）中的常数k。确定一个一次函数，需要确定一次函数定义式（k0）中的常数k和b。解这类问题的一般方法是待定系数法。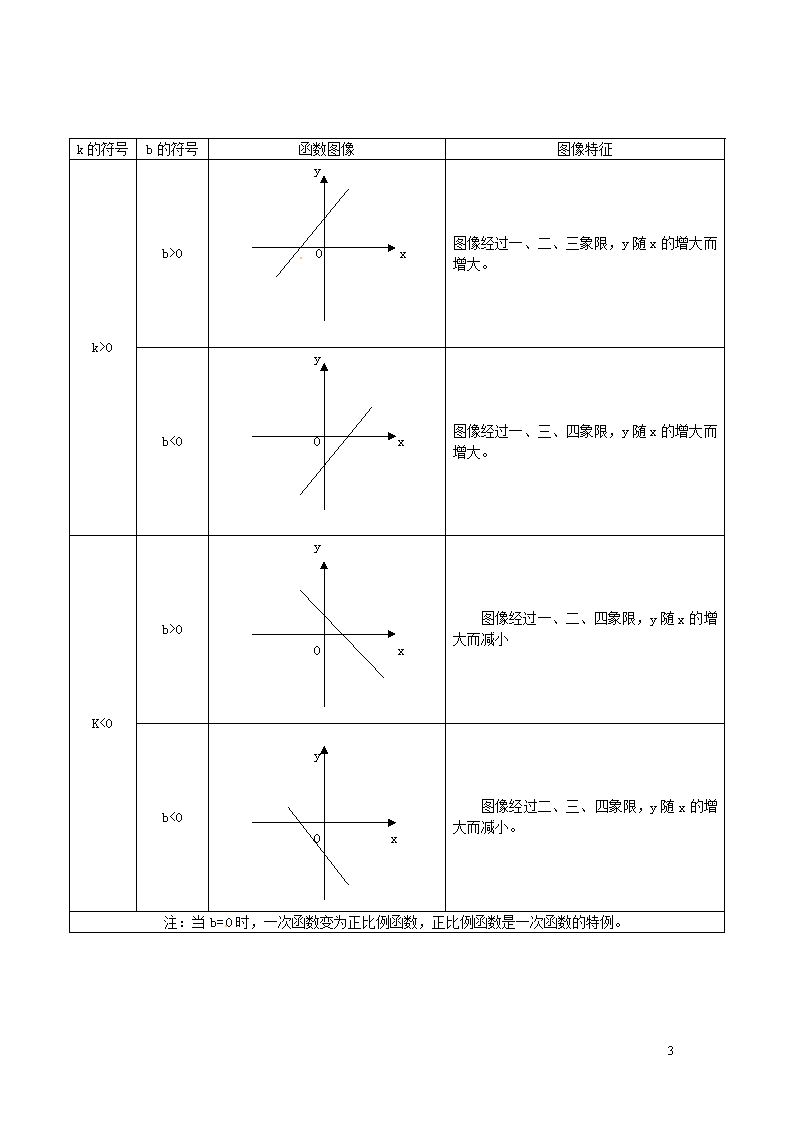‎ 3‎ k的符号 b的符号 函数图像 图像特征 k>0‎ b>0‎ ‎ y ‎ 0 x 图像经过一、二、三象限，y随x的增大而增大。‎ b<0‎ ‎ y ‎ 0 x 图像经过一、三、四象限，y随x的增大而增大。‎ K<0‎ b>0‎ ‎ y ‎ 0 x ‎ 图像经过一、二、四象限，y随x的增大而减小 b<0‎ ‎ y ‎ 0 x ‎ 图像经过二、三、四象限，y随x的增大而减小。‎ 注：当b=0时，一次函数变为正比例函数，正比例函数是一次函数的特例。‎ 3‎