2020-2021八年级数学上册等腰三角形与最短路径问题同步讲练（新人教版pdf格式） 73页

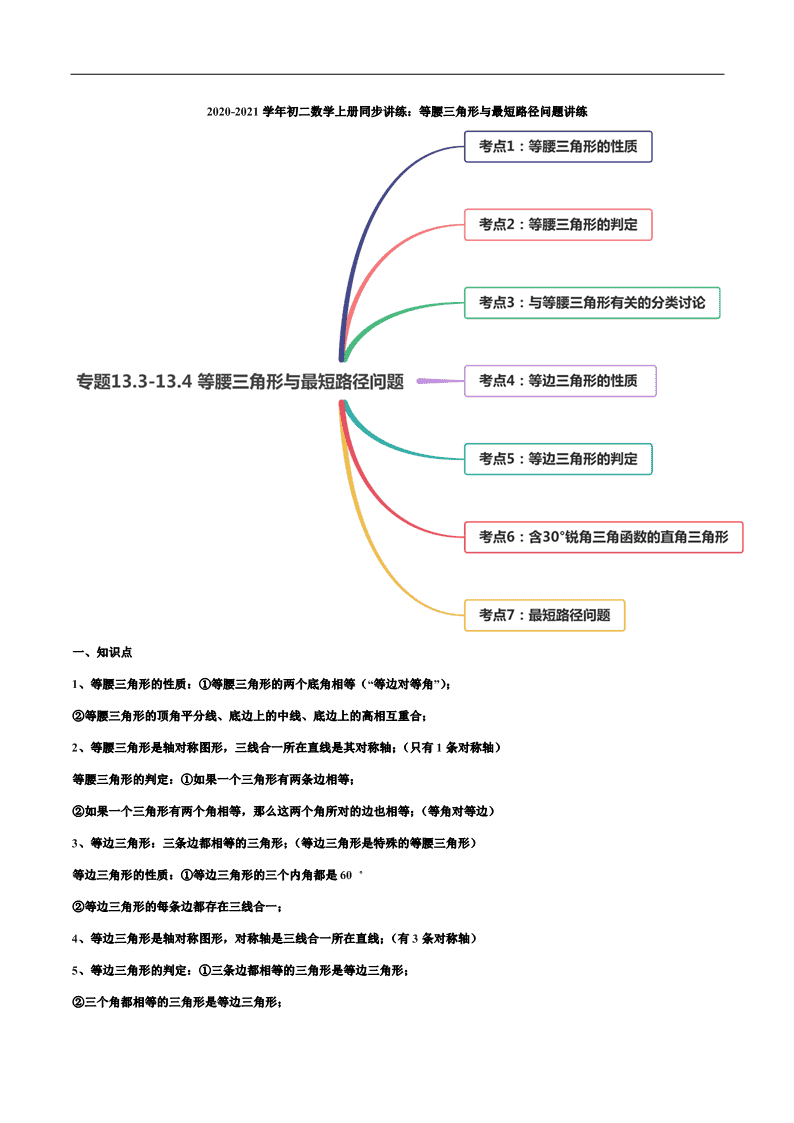
2020-2021 学年初二数学上册同步讲练：等腰三角形与最短路径问题讲练 一、知识点 1、等腰三角形的性质：①等腰三角形的两个底角相等（“等边对等角”）； ②等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合； 2、等腰三角形是轴对称图形，三线合一所在直线是其对称轴；（只有 1 条对称轴） 等腰三角形的判定：①如果一个三角形有两条边相等； ②如果一个三角形有两个角相等，那么这两个角所对的边也相等；（等角对等边） 3、等边三角形：三条边都相等的三角形；（等边三角形是特殊的等腰三角形） 等边三角形的性质：①等边三角形的三个内角都是 60〬 ②等边三角形的每条边都存在三线合一； 4、等边三角形是轴对称图形，对称轴是三线合一所在直线；（有 3 条对称轴） 5、等边三角形的判定：①三条边都相等的三角形是等边三角形； ②三个角都相等的三角形是等边三角形； ③有一个角是 60〬的等腰三角形是等边三角形； 6、在直角三角形中，如果一个锐角等于 30〬，那么它所对的直角边等于斜边的一半； 7、最短路径的选择 ①当两点在某一条 直线的两侧时,这两点的最短距离就是连接这两点的线段与直线的交点就是最短路径的点. ②当两点在某条直线的同 侧时,这两点到直线上某一 点的最短距离的作法: 作任意一个点关于这条直线的对称点,然后再连接 对称点与另一点之间的线段,与直线的交点就是最短距离的点的位置. 注意：在解决最短路径的问题时,我们通常利用平移、轴对称等变化把已知问题转化成容易解决的问 题,从而作出最短路径的 选择. 二、考点点拨与训练 考点 1：等腰三角形的性质 典例：（2020·河北河间初二期末）如图 1，△ABC 中，AD 是∠BAC 的平分线，若 AB=AC+CD，那么∠ACB 与∠B 有怎样的 数量关系？ 小明通过观察分析，形成了如下解题思路：如图 2，延长 AC 到 E，使 CE=CD，连接 DE．进而得到△ABD≌△AED，便可得 到∠ACB 与∠B 的数量关系．请结合小明的思路，写出两个角的数量关系，并证明结论． 【答案】∠ACB＝2∠ABC，证明见详解 【解析】∠ACB＝2∠ABC 证明：延长 AC 到 E，使 CE=CD，连接 DE ∴∠E＝∠CDE ∵AB=AC+CD ∴AE＝AB 又∵AD 是∠BAC 的平分线 ∴∠BAD＝∠CAD 又 AD=AD ∴△ABD≌△AED ∴∠B＝∠E 又∵∠ACB＝∠E+∠CDE ∴∠ACB＝2∠ABC 方法或规律点拨 本题考查了等腰三角形的性质，全等三角形的判定和性质，熟练掌握等腰三角形的性质是解题的关键． 巩固练习 1．（ 2020·山东芝罘初一期中）如图，△ABC 中，AB＝AC，腰 AB 的垂直平分线 DE 交 AB 于点 E，交 AC 于点 D，且∠DBC ＝15°，则∠A 的度数是 （ ） A．50° B．36° C．40° D．45° 【答案】A 【解析】解：∵AB 的垂直平分线 DE 交 AC 于 D， ∴AD=BD， ∴∠A=∠ABD， ∵AB=AC， ∴∠ABC=∠C， ∵∠DBC=15°， ∴∠ABC=∠C=∠A+15°， 在△ABC 中，∠A+∠ABC+∠C=180°， ∴∠A+∠A+15°+∠A+15°=180°， 解得∠A=50°． 故选：A． 2．（ 2020·四川成华初一期末）如图，在△ABC 中，AB=AC，∠C=70°，△AB′C′与△ABC 关于直线 EF 对称，∠CAF=10°， 连接 BB′，则∠ABB′的度数是（ ） A．30° B．35° C．40° D．45° 【答案】C 【解析】如图，连接 BB′ ∵△AB′C′与△ABC 关于直线 EF 对称， ∴△BAC≌△B′AC′， ∵AB=AC，∠C=70°， ∴∠ABC=∠AC′B′=∠AB′C′=70°， ∴∠BAC=∠B′AC′=40°， ∵∠CAF=10°， ∴∠C′AF=10°， ∴∠BAB′=40°+10°+10°+40°=100°， ∴∠ABB′=∠AB′B=40°， 故选 C． 3．（ 2020·陕西西安高新一中初一期末）如图， ABC 中， ,ABACAD 是 BAC 的角平分线， AC 的垂直平分线分 别交 ACADAB、 、 于点 E O F、 、 ，则下列结论不一定成立的是（ ） A． AD BC B． OC OD AD C． OA OB D． ACO BOF   【答案】D 【解析】∵ ,A B A C A D 是 BAC 的角平分线， ∴ AD BC ，故 A 正确； ∵EF 垂直平分 AC， ∴OA=OC， ∴AD=OA+OD=OC+OD，故 B 正确； ∵ 是 的角平分线， ∴CD=BD，AD⊥BC，即 AD 垂直平分 BC， ∴OB=OC， ∴OA=OB，故 C 正确； ∵ 是 的角平分线， ∴∠CAD=∠BAD， ∵OA=OC=OB， ∴∠ACO=∠CAD=∠BAD=∠ABO， ∵BF 与 OF 不一定相等， ∴∠BOF 与∠ABO 不一定相等， ∴∠ACO 与∠BOF 不一定相等，故 D 错误 故选：D. 4．（ 2020·四川龙泉驿初一期末）如图所示，在△ABC 中，AB＝AC，点 D 在 AC 上，且 BD＝BC＝AD，则∠A 等于( ) A．30° B．40° C．45° D．36° 【答案】D 【解析】 ∵AD＝BD， ∴∠A＝∠ABD， ∴∠BDC＝2∠A. ∵BD＝BC， ∴∠C＝∠BDC＝2∠A． ∵AB＝AC， ∴∠ABC＝∠C＝2∠A， 由三角形内角和定理，得∠A+2∠A+2∠A＝180°， 即∠A＝36°． 故选 D. 5．（ 2020·山东槐荫初一期末）如图，在第 1 个△A1BC 中，∠B＝30°，A1B＝CB；在边 A1B 上任取一点 D，延长 CA1 到 A2， 使 A1A2＝A1D，得到第 2 个△A1A2D；在边 A2D 上任取一点 E，延长 A1A2 到 A3，使 A2A3＝A2E，得到第 3 个△A2A3E，…按 此做法继续下去，则第 n 个三角形中以 An 为顶点的底角度数是（ ） A．（ 1 2 ）n•75° B．（ ）n﹣1•65° C．（ ）n﹣1•75° D．（ ）n•85° 【答案】C 【解析】解：∵在△CBA1 中，∠B＝30°，A1B＝CB， ∴∠BA1C＝ 180 2 B   ＝75°， ∵A1A2＝A1D，∠BA1C 是△A1A2D 的外角， ∴∠DA2A1＝ ∠BA1C＝ ×75°； 同理可得， ∠EA3A2＝（ ）2×75°，∠FA4A3＝（ ）3×75°， ∴第 n 个三角形中以 An 为顶点的底角度数是（ ）n﹣1×75°． 故选：C． 6．（ 2020·河南罗山初二期末）如图，AD，CE 分别是△ABC 的中线和角平分线．若 AB=AC，∠CAD=20°，则∠ACE 的度数 是（ ） A．20° B．35° C．40° D．70° 【答案】B 【解析】∵AD 是△ABC 的中线，AB=AC，∠CAD=20°， ∴∠CAB=2∠CAD=40°，∠B=∠ACB= 1 2 （180°-∠CAB）=70°． ∵CE 是△ABC 的角平分线， ∴∠ACE= ∠ACB=35°． 故选 B． 7．（ 2020·山东中区济南外国语学校初二期末）如图，在 ABC△ 中， A B A C ， 130BAC ，AB 的垂直平分线交 AB 于点 E，交 BC 于点 F，连接 AF，则 FAB 的度数（ ） A． 50  B． 35 C． 30  D． 25 【答案】D 【解析】解：∵AB=AC，∠BAC=130°， ∴∠B=（180°-130°）÷2=25°， ∵EF 垂直平分 AB， ∴BF=AF， ∴∠BAF=∠B=25°． 故选 D. 8．（ 2020·浙江南浔初三其他）如图“三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能 三等分任一角．这个三等分角仪由两根有槽的棒 OA，OB 组成，两根棒在 O 点相连并可绕 O 转动，C 点固定，OC=CD=DE， 点 D、E 可在槽中滑动，若∠BDE=72°，则∠CDE 的度数是（ ） A．63° B．65° C．75° D．84° 【答案】D 【解析】∵OC=CD=DE， ∴∠O=∠ODC，∠DCE=∠DEC， ∴∠DCE=∠O+∠ODC=2∠ODC， ∵∠O+∠OED=3∠ODC=∠BDE=72°， ∴∠ODC=24°， ∵∠CDE+∠ODC=180°﹣∠BDE=108°， ∴∠CDE=108°﹣∠ODC=84°． 故选：D． 9．（ 2020·山东历下初一期末）如图，已知∠AOB＝10°，且 OC＝CD＝DE＝EF＝FG＝GH，则∠BGH＝ （ ） A．50° B．60° C．70° D．80° 【答案】B 【解析】解：∵∠AOB＝10°，OC＝CD＝DE＝EF＝FG＝GH， ∴∠ODC=10°， ∴∠BCD=∠AOB+∠ODC=20°， ∵CD=DE， ∴∠DEC=∠BCD=20°， ∴∠ADE=∠CED+∠AOB=30°， ∵ED=EF， ∴∠EFD=30°， ∴∠BEF=∠EFD+∠AOB=40°， ∵FE=FG， ∴∠FGE=40°， ∴∠GFH=∠FGE+∠AOB=50°， ∵GF=GH， ∴∠GHF=50°， ∴∠BGH=∠GHF+∠AOB=60°， 故选 B． 10．（ 2019·河南宜阳初二期末）如图，在△ABC 中，AB=AD=DC，∠B=70°，则∠C=______． 【答案】35° 【解析】∵△ABD 中，AB=AD，∠B=70°， ∴∠B=∠ADB=70°， ∴∠ADC=180°﹣∠ADB=110°， ∵AD=CD， ∴∠C=（180°﹣∠ADC）÷2=（180°﹣110°）÷2=35°. 11．（ 2020·广东龙岗初一期末）如图，点 O 为线段 AB 上的任意一点（不于 A、B 重合），分别以 AO，BO 为一腰在 AB 的同 侧作等腰△AOC 和△BOD，OA=OC，OB=OD，∠AOC 与∠BOD 都是锐角，且∠AOC=∠BOD，AD 与 BC 交于点 P，AD 交 CO 于点 M，BC 交 DO 于点 N． （1）试说明：CB=AD； （2）若∠COD=70°，求∠APB 的度数． 【答案】（1）证明见解析；（2）∠APB=125° 【解析】 （1）∵∠AOC=∠BOD， ∴∠AOD=∠COB， 又∵OA=OC，OB=OD， ∴△AOD≌△COB（SAS）， ∴CB=AD； （2）∵∠COD=70°， ∴∠AOC=∠BOD= 180 70 2    =55°， ∴∠AOD=∠COD+∠BOD=125°=∠COB， ∵△AOD≌△COB， ∴∠DAO=∠BCO， ∴∠DAO+∠CBO=∠BCO+∠CBO， ∴180°-∠APB=180°-∠COB， ∴∠APB=∠COB=125°． 12．（ 2020·陕西渭滨初一期末）如图，在△ABC 中，∠ACB＝90°，CA＝CB，延长 BC 至 D，使 BD＝BA，连接 AD．点 E 在 AC 上，且 CE＝CD，连接 BE 并延长 BE 交 AD 于点 F． （1）求证：△ACD≌△BCE； （2）求证：BF 是 AD 的垂直平分线； （3）连接 DE，若 AB＝10，求△DCE 的周长． 【答案】（1）见解析；（2）见解析；（3）10 【解析】（1）证明： ∵∠ACB＝90°，CD 是 BC 延长线， ∴∠ACD=∠ACB=90°． 在△ACD 和△BCE 中， CACB ACDBCE CDCE      ， ∴△ACD≌△BCE（SAS）． （2）由（1）知△ACD≌△BCE 则∠CAD=∠CBE， 又∵∠AEF=∠BEC， ∴在△AEF 与△BEC 中∠AFE=∠BCE＝90°， ∴BF⊥AD， 又∵BD＝BA， ∴BF 是 AD 的垂直平分线． （3）∵EF 是 AD 的垂直平分线， ∴EA=ED， 又∵BC=AC，AB=BD=10， ∴△DEC 的周长=ED+EC+CD=AC+CD=BC+CD=AB=10． 考点 2：等腰三角形的判定 典例：（2020·黑龙江牡丹江）在等腰 ABC 中， ABBC ，点 D，E 在射线 BA 上，BDDE ，过点 E 作 //EFBC ， 交射线 CA 于点 F．请解答下列问题： （1）当点 E 在线段 AB 上， CD 是 ACB△ 的角平分线时，如图①，求证： AEBCCF；（提示：延长 ， FE 交于点 M．） （2）当点 E 在线段 的延长线上， 是 的角平分线时，如图②；当点 E 在线段 的延长线上， 是 的外角平分线时，如图③，请直接写出线段 AE ， BC ， CF 之间的数量关系，不需要证明； （3）在（1）、（ 2）的条件下，若 26DE AE，则 CF  ___________． 【答案】（1）见解析；（2）BC=AE+CF 或 AE=CF+BC；（ 3）18 或 6． 【解析】（1）如图①，延长 CD ， FE 交于点 M． ∵ A B B C ， //EF BC ∴∠A=∠BCA=∠EFA， ∴AE=EF ∴ //M F B C ∴∠MED=∠B， ∠M=∠BCD 又∵∠FCM=∠BCM， ∴∠M=∠FCM ∴CF=MF 又∵BD=DE ∴  MEDCBDAAS ∴ME=BC ∴CF=MF=ME+EF=BC+AE 即 AE+BC=CF； （2）当点 E 在线段 BA 的延长线上， 是 ACB△ 的角平分线时，BC=AE+CF， 如图②，延长 ，EF 交于点 M． 由①同理可证 ， ∴ME=BC 由①证明过程同理可得出 MF=CF，AE=EF， ∴BC=ME=EF+MF=AE+CF； 当点 E 在线段 BA 的延长线上， CD 是 A C B△ 的外角平分线时，AE=CF+BC. 如图③，延长 交 EF 于点 M， 由上述证明过程易得  MEDCBDAAS ，BC=EM， CF=FM， 又∵AB=BC， ∴∠ACB=∠CAB=∠FAE ∵ //EFBC ∴∠F=∠FCB， ∴EF=AE， ∴AE=FE=FM+ME=CF+BC （3）CF=18 或 6 当 DE=2AE=6 时，图①中，由（1）得：AE=3，BC=AB=BD+DE+AE=15， ∴CF=AE+BC=3+15=18； 图②中，由（2）得：AE=AD=3，BC=AB=BD+AD=9， ∴CF=BC-AE=9-3=6； 图③中，DE 小于 AE，故不存在． 故答案为 18 或 6． 方法或规律点拨 本题是考查了角平分线、平行线和等腰三角形及全等三角形的综合题，关键是添加恰当的辅助线，构建角平分线加平行的模 型，是一道较好的中考真题． 巩固练习 1．（ 2019·薛城区祁连山路中学初一期中）如图，在 ABC 中， ABC 和 ACB 的平分线交于点 O ，过点 作 //EF BC ， 交 AB 于 E ，交 AC 于 F ，若 3 , 2B E C F，则线段 EF 的长为（ ） A．8 B．． 7 C．6 D．5 【答案】D 【解析】∵∠ABC、∠ACB 的平分线相交于点 O， ∴∠OBE=∠OBC，∠OCF=∠OCB， ∵EF∥BC， ∴∠EOB=∠OBC，∠FOC=∠BCO， ∴∠OBE=∠EOB，∠FCO=∠FOC， ∴BE=OE，FC=FO， ∴EF=EO+FO， 即 EF=BE+CF． ∵ ∴EF=5 ， 故选 D． 2．（ 2020·湖北黄州初二期末）如图，∠ABC，∠ACB 的平分线相交于点 F，过点 F 作 DE∥BC，交 AB 于 D，交 AC 于 E， 那么下列结论：①△BDF，△CEF 都是等腰三角形；②DE=BD+CE；③△ADE 的周长为 AB+AC；④BD=CE．其中正确的是 ____． 【答案】①②③ 【解析】解：①∵BF 是∠ABC 的角平分线， ∴∠ABF＝∠CBF， 又∵DE∥BC， ∴∠CBF＝∠DFB， ∴DB＝DF 即△BDF 是等腰三角形， 同理∠ECF＝∠EFC， ∴EF＝EC， ∴△BDF，△CEF 都是等腰三角形；故正确． ②∵△BDF，△CEF 都是等腰三角形， ∴DF＝DB，EF＝EC， ∴DE＝DF＋EF＝BD＋EC，故正确． ③∵①△BDF，△CEF 都是等腰三角形 ∴BD＝DF，EF＝EC， △ADE 的周长＝AD＋DF＋EF＋AE＝AD＋BD＋AE＋EC＝AB＋AC；故正确， ④无法判断 BD＝CE，故错误， 故答案为：①②③． 3．（ 2020·广东英德初二期中）如图所示，在四边形 A B C D 中， //ADBC ， 5BC  ， 4AB  ， AE 平分 BAD 交 BC 边于点 E ，求 CE 的长． 【答案】1 【解析】解： //ADBC ， DAEBEA?? ． AE∵ 平分 ， DAE BAE   ． BAEBEA  ， BE AB． 5 4 1CE BC BE      ． 4．（ 2020·广东高州初三月考）如图，已知等腰△ABC 顶角∠A=36°． （1）尺规作图：在 AC 上作一点 D，使 AD=BD；（保留作图痕迹，不必写作法和证明） （2）求证：△BCD 是等腰三角形． 【答案】（1）见解析；（2）△BCD 是等腰三角形 【解析】（1）如图 1，作 AB 的垂直平分线，分别以点 A、B 为圆心，以大于 2 AB 为半径在 AB 上方画弧，在 AB 上方两圆 弧交点为点 M，分别以点 A、B 为圆心以大于 为半径在 AB 下方画弧，在 AB 下方两圆弧交点为点 N．过点 M、N 作直 线 MN，交 AC 于点 D，点 D 即为所求． （2）∵在等腰△ABC 顶角∠A=36° ∴  1 18036722ABCACB   ∵AD=BD ∴∠ABD=∠A=36° 则∠DBC=36° 在△BCD 中∠ACB=72° ∠DBC=36° ∠BDC=72°=∠ACB ∴△BCD 是等腰三角形 5．（ 2020·广东佛山初二月考）如图，在 ABC 和 DCB 中， 90AD   ， AC BD ，AC 与 BD 相交于点 O. （1）求证： A B C D C B   ； （2） OBC 是何种三角形？ 【答案】（1）见解析；（2）△OBC 是等腰三角形，理由见解析. 【解析】（1）∵∠A＝∠D＝90°， ∴在 Rt△ABC 和 Rt△DCB 中， AC BD BC CB    ， ∴Rt△ABC≌Rt△DCB（HL）； （2）△OBC 是等腰三角形， 理由：∵Rt△ABC≌Rt△DCB， ∴∠ACB＝∠DBC， ∴OB＝OC， ∴△OBC 是等腰三角形. 6．（ 2020·江苏海安初二月考）已知∠MAN=30°，点 B 在射线 AM 上，且 AB=6，点 C 在射线 AN 上． （1）若△ABC 是直角三角形，求 AC 的长； （2）若△ABC 是等腰三角形，则满足条件的 C 点有 个； （3）设 BC=x，当△ABC 唯一确定时， 直接写出 x 的取值范围． 【答案】（1） 43或 33；（ 2）3；（ 2）x =3 或 x≥6 【解析】（1）当∠ABC=90°时，如图所示， ∵∠A=30° ∴BC= 1 2 AC ∴设 BC=x，则 AC=2x 在 Rt△ABC 中，由勾股定理得 2236 4xx 解得 x= 23 ∴AC= 43 当∠ACB=90°时，如图所示， ∵∠A=30° ∴BC= 1 32 AB  ∴AC= 33 （2）当 AB 为腰时，等腰三角形有两个，如图， 当 AB 为底时，等腰三角形有 1 个，如图 ∴△ABC 是等腰三角形，则满足条件的 C 点有 3 个 （3）根据三角形三边关系可知，△ABC 唯一确定时，由（1）、（ 2）得，BC=3 或 BC≥6. 故 x=3 或 x≥6. 7．（ 2020·黑龙江南岗初三其他）已知:在 ABC 中, AC AB BC<< ,线段 AB 的垂直平分线交 BC 于点 D ,点 E 在 上， 且 B E A B ,连接 ,,3.ADAEAECBAD  1 如图 1 ,求证: ;A D A E  2 如图 2,当 2BCAE 时.在不添加任何辅助线情况下,请直接写出图 2 中的四个等腰三角形． 【答案】 见解析； ABD ， ABE ， ADE ， A C D 【解析】 证明：令 B  ， 线段 的垂直平分线交 于点 ， ADBD， BADB   ， 2ADE B BAD      ， 33AEC BAD     ， 32BAE AEC B          ， A B B E ， 2AEBBAEADE    ， AD AE；  2 如图 2， ∵AB 的垂直平分线交 BC 于 D， ∴AD=BD， ∴ ABD 是等腰三角形； ∵AB=BE， ∴△ABE 是等腰三角形； 由（1）知 2AEBBAEADE    ， ∴△ADE 是等腰三角形； ∵ 2BAE ， BAD ， ∴ DAE  ∵ 2BCAE ， ∴ 1 2CAE ， ∴ 3 2DAC ， 3 2CAEBCAE    ， ∴∠DAC=∠C， ∴AD=CD， ∴△ACD 是等腰三角形； ∴图中的等腰三角形是： ， ABE ， ADE ， ACD . 8．（ 2020·黑龙江哈尔滨初三二模）图 1、图 2 分别是 86 的网格，网格中每个小正方形的边长均为 1，线段 AB 的端点在 小正方形的顶点上，请在图 1、图 2 中各画一个图形，分别满足以下要求： （1）在图 1 中画一个 ABC ，使得 是面积为 10 的直角三角形，所画图形的各顶点必须在小正方形的顶点上； （2）在图 2 中画一个以线段 为一边的钝角等腰三角形，并且面积等于 10，所画等腰三角形的各顶点必须在小正方形的 顶点上． 【答案】（1）见解析；（2）见解析 【解析】（1）图形如下(答案不唯一)： （2）图形如下： 9．（ 2020·镇江实验学校初三一模）（1）如图 1,△ABC 中,∠C=90°,请用直尺和圆规作一条直线,把△ABC 分割成两个等腰三角 形(不写作法,但须保留作图痕迹). （2）已知内角度数的两个三角形如图 2,图 3 所示.请你判断,能否分别画一条直线把它们分割成两个等腰三角形?若能,请写出 分割成的两个等腰三角形顶角的度数. 【答案】（1）见解析；（2）图 2 能画一条直线分割成两个等腰三角形，分割成的两个等腰三角形的顶角分别是 132°和 84°； 图 3 不能分割成两个等腰三角形. 【解析】（1）如图,直线 CE 即为所求； （2）图 2 能画一条直线分割成两个等腰三角形, 分割成的两个等腰三角形的顶角分别是 132°和 84°. 图 3 不能分割成两个等腰三角形. 10．（ 2018·额尔古纳市三河中学初二期末）如图，在四边形 ABCD 中， //AD BC ， E 是 AB 的中点，连接 DE 并延长 交 CB 的延长线于点 F ，点 G 在边 BC 上，且 GDFADF ． （1）求证： ADE ≌ BFE ． （2）连接 EG ，判断 与 DF 的位置关系并说明理由． 【答案】（1）见解析；（2） EGDF ，见解析 【解析】（1）证明：∵AD∥BC， ∴∠ADE＝∠BFE， ∵E 为 AB 的中点， ∴AE＝BE， 在△ADE 和△BFE 中， ADE BFE AED BEF AE BE         ， ∴△ADE≌△BFE（AAS）； （2）EG⊥DF， 理由如下：连接 EG， ∵∠GDF＝∠ADE，∠ADE＝∠BFE， ∴∠GDF＝∠BFE， ∴DG＝FG， 由（1）得：△ADE≌△BFE ∴DE＝FE， 即 GE 为 DF 上的中线， 又∵DG＝FG， ∴EG⊥DF． 考点 3：与等腰三角形有关的分类讨论 典例：（2020·福建宁德初一期末）如图，已知等腰△ABC 中，AB=AC，∠A＜90°，CD 是△ABC 的高，BE 是△ABC 的角平 分线，CD 与 BE 交于点 P．当∠A 的大小变化时，△EPC 的形状也随之改变． （1）当∠A=44°时，求∠BPD 的度数； （2）设∠A=x°，∠EPC=y°，求变量 y 与 x 的关系式； （3）当△EPC 是等腰三角形时，请直接写出∠A 的度数． 【答案】（1）56°；（ 2）y= 45 4 x ；（ 3）36°或 180 7 °. 【解析】解：（1）∵AB=AC，∠A=44°， ∴∠ABC=∠ACB=（180-44）÷2=68°， ∵CD⊥AB， ∴∠BDC=90°， ∵BE 平分∠ABC， ∴∠ABE=∠CBE=34°， ∴∠BPD=90-34=56°； （2）∵∠A=x°， ∴∠ABC=（180°-x°）÷2=（ 90 2 x ）°， 由（1）可得：∠ABP= 1 2 ∠ABC=（ 45 4 x ）°，∠BDC=90°， ∴∠EPC=y°= ∠BPD=90°-（ ）°= （ 45 4 x ）°， 即 y 与 x 的关系式为 y= ； （3）①若 EP=EC， 则∠ECP=∠EPC=y， 而∠ABC=∠ACB= ，∠ABC+∠BCD=90°， 则有： +（ -y）=90°，又 y= ， ∴ + -（ ）=90°， 解得：x=36°； ②若 PC=PE， 则∠PCE=∠PEC=（180-y）÷2= 90 2 y ， 由①得：∠ABC+∠BCD=90°， ∴ +[ -（ ）]=90，又 y= ， 解得：x= 180 7 °； ③若 CP=CE， 则∠EPC=∠PEC=y，∠PCE=180-2y， 由①得：∠ABC+∠BCD=90°， ∴ + -（180-2y）=90，又 y= ， 解得：x=0，不符合， 综上：当△EPC 是等腰三角形时，∠A 的度数为 36°或 180 7 °. 方法或规律点拨 本题考查了等腰三角形的性质，二元一次方程组的应用，高与角平分线的定义，有一定难度，关键是找到角之间的等量关系. 巩固练习 1．（ 2020·河北河间初二期末）已知实数 x，y 满足|x﹣4|+（y﹣8）2＝0，则以 x，y 的值为两边长的等腰三角形的周长是（ ） A．20 或 16 B．20 C．16 D．以上答案均不对 【答案】B 【解析】解：根据题意得，x﹣4＝0，y﹣8＝0， 解得 x＝4，y＝8， ①4 是腰长时，三角形的三边分别为 4、4、8， ∵4+4＝8， ∴不能组成三角形； ②4 是底边时，三角形的三边分别为 4、8、8， 能组成三角形，周长＝4+8+8＝20． 所以，三角形的周长为 20． 故选：B． 2．（ 2020·鸡东县第三中学初一期中）已知等腰三角形的周长为 17cm，一边长为 4cm，则它的腰长为（ ） A．4cm B．6.5cm 或 9cm C．6.5cm D．4cm 或 6.5cm 【答案】C 【解析】解：若腰长为 4，则底边长为：17-4-4=9， ∵4+4=8＜9， ∴不能组成三角形，舍去； 若底边长为 4，则腰长为： 17 4 2  =6.5， ∵4+6.5  6.5， ∴能组成三角形， ∴该等腰三角形的腰长为：6.5． 故答案为 C． 3．（ 2020·山东中区济南外国语学校初二期末）如果一个等腰三角形的两边长为 4、9，则它的周长为( ) A．17 B．22 C．17 或 22 D．无法计算 【答案】B 【解析】解：（1）若 4 为腰长，9 为底边长， 由于 4+4＜9，则三角形不存在； （2）若 9 为腰长，则符合三角形的两边之和大于第三边． 所以这个三角形的周长为 9+9+4=22． 故选：B． 4．（ 2020·广东龙岗初一期末）如果等腰三角形的一个内角为 50°，那么其它两个内角为（ ） A．50°，80° B．65°，65° C．50°，65° D．50°，80°或 65°，65° 【答案】D 【解析】解：当 50°是底角时，顶角为 180°-50°×2=80°， 当 50°是顶角时，底角为（180°-50°）÷2=65°． 故这个等腰三角形的另外两个内角度数分别是 50°，80°或 65°，65°． 故选：D． 5．（ 2020·山东招远初一期末）等腰三角形一腰上的高与另一腰的夹角为 60 ，则顶角的度数为（ ） A． 30° B． C． 或 120  D． 或 150 【答案】D 【解析】解：①当为锐角三角形时，如图 1， ∵∠ABD=60°，BD⊥AC， ∴∠A=90°-60°=30°， ∴三角形的顶角为 30°； ②当为钝角三角形时，如图 2， ∵∠ABD=60°，BD⊥AC， ∴∠BAD=90°-60°=30°， ∵∠BAD+∠BAC=180°， ∴∠BAC=150° ∴三角形的顶角为 150°， 故选：D． 6．（ 2018·河南孟津初二期末）如图，已知每个小方格的边长为 1，A，B 两点都在小方格的格点（顶点）上，请在图中找一 个格点 C，使△ABC 是以 AB 为腰的等腰三角形，这样的格点 C 有（ ） A．4 个 B．5 个 C．6 个 D．7 【答案】C 【解析】当 AB 为腰时，分别以 A、B 点为顶点，以 AB 为半径作圆，可找出格点点 C 的个数有 6 个； 使△ABC 是以 AB 为腰的等腰三角形，这样的格点 C 有 6 个． 故选 C． 7．（ 2019·河南偃师初二期末）在一张长为 10cm，宽为 8cm 的矩形纸片上，要剪下一个腰长为 5cm 的等腰三角形（要求：等 腰三角形的一个顶点与矩形的顶点 A 重合，其余的两个顶点都在矩形边上），这个等腰三角形有几种剪法（ ） A．1 B．2 C．3 D．4 【答案】B 【解析】有两种情况： ①当∠A 为顶角时，如图 1，此时 AE=AF=5cm． ②当∠A 为底角时，如图 2，此时 AE=EF=5cm． 故选 B． 8．（ 2020·四川前锋初三其他）在平面直角坐标系 xOy 中，已知点 P（2，2），点 Q 在 y 轴上，△PQO 是等腰三角形，则满足 条件的点 Q 共有 A．5 个 B．4 个 C．3 个 D．2 个 【答案】B 【解析】如图：满足条件的点 Q 共有（0，2）（ 0，2 2 ）（ 0，-2 ）（ 0，4）． 故选 B． 9．（ 2020·贵州松桃初三其他）平面直角坐标系中，已知 A（2，2）、 B（4，0）．若在坐标轴上取点 C，使△ABC 为等腰三角形， 则满足条件的点 C 的个数是（ ） A．5 B．6 C．7 D．8 【答案】A 【解析】构造等腰三角形，①分别以 A，B 为圆心，以 AB 的长为半径作圆；②作 AB 的中垂线．如图，一共有 5 个 C 点， 注意，与 B 重合及与 AB 共线的点要排除．故答案选 A. 10．（ 2020·四川内江初一期末）已知等腰三角形的两边长是 5 和 12，则它的周长是______________； 【答案】29 【解析】解：当 5 为腰长时， ∵5+5<12，故不能组成三角形， 当 12 为腰长时，边长分别为：5，12，12， ∵5+12>12，故能组成三角形， 故周长为：5+12+12=29； 故答案为：29． 考点 4：等边三角形的性质 典例：（2020·四川凉山中考真题）如图，点 P、Q 分别是等边 ABC 边 AB、BC 上的动点（端点除外），点 P、点 Q 以相同 的速度，同时从点 A、点 B 出发． （1）如图 1，连接 AQ、CP 求证： A B Q C A P   （2）如图 1，当点 P、Q 分别在 AB、BC 边上运动时，AQ、CP 相交于点 M， Q M C 的大小是否变化？若变化，请说明 理由；若不变，求出它的度数 （3）如图 2，当点 P、Q 在 AB、BC 的延长线上运动时，直线 AQ、CP 相交于 M， 的大小是否变化？若变化，请 说明理由；若不变，求出它的度数． 【答案】（1）证明见解析；（2）不变；60°；（ 3）不变；120°． 【解析】解：（1）证明：∵三角形 ABC 为等边三角形， ∴AB=AC，∠ABC=∠CAB=60°， ∵点 P、点 Q 以相同的速度，同时从点 A、点 B 出发， ∴BQ=AP， 在△ABQ 与△CAB 中， ABAC ABCCAB BQAP      ∴  ABQCAPSAS  ． （2）角度不变，60°，理由如下： ∵ ∴∠CPA=∠AQB， 在△AMP 中， ∠AMP=180°-（∠MAP+∠CPA）=180°-（∠MAP+∠AQB）=∠ABC=60°， ∴∠QMC=∠AMP=60°， 故∠QMC 的度数不变，度数为 60°． （3）角度不变，120°，理由如下： 当点 P、Q 在 AB、BC 的延长线上运动时， 有 AP=BQ，∴BP=CQ ∵∠ABC=∠BCA=60°， ∴∠CBP=∠ACQ=120°， BCAC CBPACQ BPCQ      ∴  CBPACQSAS△ △ ∴∠Q=∠P， ∵∠QCM=∠BCP， ∴∠QMC=∠CBP=120°， 故∠QMC 的度数不变，度数为 120°． 方法或规律点拨 本题考查等边三角形的性质、全等三角形的判定和性质、三角形内角和定理，灵活运用等边三角形的性质证全等是解题的关 键． 巩固练习 1．（ 2020·内蒙古林西初二期末）如图，已知 C 是线段 AB 上的任意一点（端点除外），分别以 AC、BC 为边并且在 AB 的同一 侧作等边△ACD 和等边△BCE，连接 AE 交 CD 于 M，连接 BD 交 CE 于 N．给出以下三个结论：①AE=BD ； ②CN=CM； ③ MN∥AB； ④∠CDB=∠NBE． 其中正确结论的个数是（ ） A．4 B．3 C．2 D．1 【答案】A 【解析】∵△ACD 和△BCE 是等边三角形 ∴∠ACD=∠BCE=60°，AC=DC，EC=BC ∴∠ACD+∠DCE=∠DCE+∠ECB 即∠ACE=∠DCB ∴△ACE≌△DCB（SAS） ∴AE=BD，故①正确； ∴∠EAC=∠NDC ∵∠ACD=∠BCE=60° ∴∠DCE=60° ∴∠ACD=∠MCN=60° ∵AC=DC ∴△ACM≌△DCN（ASA） ∴CM=CN，故②正确； 又∠MCN=180°-∠MCA-∠NCB=180°-60°-60°=60° ∴△CMN 是等边三角形 ∴∠NMC=∠ACD=60° ∴MN∥AB，故③正确； 在△DCN 和△BNE， ∠DNC+∠DCN+∠CDB=180° ∠ENB+∠CEB+∠NBE=180° ∵∠DNC=∠ENB，∠DCN=∠CEB ∴∠CDB=∠NBE，故④正确． 故选：A． 2．（ 2020·山东槐荫初一期末）如图，△DAC 和△EBC 均是等边三角形，A、C、B 三点共线，AE 与 BD 相交于点 P，AE 与 BD 分别与 CD、CE 交于点 M、N，有如下结论：①△ACE≌△DCB；②∠DPA＝60°；③AC＝DN；④EM＝BN；⑤DC∥EB，其 中正确结论是__________（填序号） 【答案】①②④⑤ 【解析】解：∵△DAC 和△EBC 都是等边三角形， ∴∠ACD=∠BCE=60°， ∴∠ACE=∠DCB=120°， 在△ACE 与△DCB 中， AC DC ACE DCB CB CE    ＝ ＝ ＝ ∴△ACE≌△DCB（SAS），故①正确； 在△DMP 和△ACM 中 ∵△ACE≌△DCB， ∴∠BDC=∠EAC 又∠DMP=∠AMC ∴∠DPA=∠DCA=60°，故②正确； ∵△ACE≌△DCB， ∴∠BDC=∠EAC 又∠ACD=∠BCE=60°，AC=CD 在△ACM 和△DCN 中 BDCEAC DCAC ACDBCE       ∴△ACM≌△DCN（ASA） ∴AM=DN 又根据三角形外角性质得到∠AMC＞∠MCE， 则∠AMC＞∠ACM， ∴AC＞AM ∴AC＞DN，故③错误； 由②中△ACM≌△DCN 可得 AM=DN 又△ACE≌△DCB ∴AE=DB ∴EM=BN，故④正确； ∵△DAC 和△EBC 均是等边三角形， ∴∠ACD=∠BCE=60°， ∴∠DCE=60°， ∴∠DCE=∠BEC， ∴CD∥BE，故⑤正确． 故答案为：①②④⑤ 3．（ 2020·武汉市梅苑学校初二期中）如图， ABC 和 C D E△ 都是等边三角形，∠EBD=78°，则∠AEB=_________度． 【答案】138 【解析】解：∵△ABC 和△CDE 都是等边三角形， ∴BC=AC，∠ABC=∠ACB=∠BAC=∠DCE=60°，CD=CE， ∴∠BCD=∠ACE， 在△BCD 和△ACE 中， BCAC BCDACE CDCE      ， ∴△BCD≌△ACE（SAS）， ∴∠CBD=∠CAE， ∵∠EBD=78°， ∴∠CBD=∠ABE+（78°-60°） ∴∠ABE=∠CAE-18°， ∵∠ABE+∠BAE=∠CAE+∠BAE-18°=∠BAC-18°=42°， ∴∠AEB=180°-42°=138°； 故答案为：138． 4．（ 2020·河南嵩县初二期末）如图，在等边三角形 ABC 中，点 D 在边 AB 上，点 E 在边 AC 上，将△ADE 折叠，使点 A 落在 BC 边上的点 F 处，则∠BDF+∠CEF＝_____． 【答案】120° 【解析】∵三角形 ABC 是等边三角形， ∴∠A=60º， ∴∠ADE+∠AED=180º-60º=120º， 由折叠性质得：∠ADE=∠EDF,∠AED=∠DEF， ∴∠BDF+∠CEF=(180º-2∠ADE)+(180º-2∠AED) =360º-2(∠ADE+∠AED) =360º-240º =120º， 故答案为：120º． 5．（ 2020·广东新丰初三其他）如图，点 1236,,, AAAA 在射线 OA 上，点 123,,,  kBBBB 在射线 OB 上， 1 1OB  ， 1 30AOB ，△ 12A B B 、△ 223A B B 、  △ 1nnnABB  均为等边三角形，则 20192020AA 的长为__． 【答案】 201823 【解析】解：∵△A1B1B2 是等边三角形， ∴∠A1B1B2＝60°， ∵∠A1OB1＝30° ∴∠OA1B1＝30°， ∴B1A1＝OB1＝1， ∵∠OA1B1＝30°，∠B1A1B2＝60°， ∴∠B2A1A2＝90°， ∵∠A2B2B3＝60°， ∴∠A1B2A2＝60°， ∴A1A2＝ 3 A1B2＝ ＝20 ，B2A2＝2A1B2＝2＝21， 同理 A2A3＝21 ，A3B3＝2A2B3＝4＝22，A3A4＝22 ，A4B4＝2A3B4＝8＝23， … 以此类推，AnAn＝2n−1 ， ∴A2019A2020 的长为 22018 ， 故答案为：22018 ． 6．（ 2020·宁夏银川市教育局初三其他）如图，是由 9 个等边三角形拼成的一个六边形，如果中间最小的等边三角形的边长是 1，则右上角的最大的正三角形的边长是_____． 【答案】6 【解析】如图，设第二小的等边三角形的边长为 x，而中间的小等边三角形的边长是 1， 所以其它等边三角形的边长分别 x+1，x+2，x+3， 由图形得，x+3=2x， 解得 x=3， 则 x+3=6， 故答案为：6． 7．（ 2020·福建安溪初三二模）如图，△ABC 与△ADE 均为等边三角形，点 B、D、E 在同一直线上，连接 CE．求证：BD＝ CE． 【答案】证明见详解 【解析】证明：连接 CE， ∵△ABC 和△ADE 为等边三角形， ∴AB=AC，AD=AE，∠BAC=∠DAE=60°， ∴∠BAC-∠DAC=∠DAE-∠DAC， 即∠BAD=∠CAE， 在△BAD 和△CAE 中， A B A C B A D C A E A D A E     ＝ ＝ ＝ ∴△BAD≌△CAE（SAS） ∴BD=CE． 8．（ 2020·山东章丘初一期末）(1)问题发现：如图 1，△ACB 和△DCE 均为等边三角形，点 A、D、E 在同一直线上，连接 BE． ①请直接写出∠AEB 的度数为_____； ②试猜想线段 AD 与线段 BE 有怎样的数量关系，并证明； (2)拓展探究：图 2， △ACB 和△DCE 均为等腰三角形，∠ACB＝∠DCE＝90°，点 A、D、E 在同－直线上， CM 为△DCE 中 DE 边上的高，连接 BE，请判断∠AEB 的度数线段 CM、AE、BE 之间的数量关系，并说明理由． 【答案】（1）①60°；②AD=BE.证明见解析；（2）∠AEB＝90°；AE=2CM+BE；理由见解析. 【解析】（1）①∵∠ACB=∠DCE，∠DCB=∠DCB， ∴∠ACD=∠BCE， 在△ACD 和△BCE 中， ACBC ACDBCE CDCE      , ∴△ACD≌△BCE， ∴AD=BE，∠CEB=∠ADC=180°−∠CDE=120°， ∴∠AEB=∠CEB−∠CED=60°； ②AD=BE. 证明：∵△ACD≌△BCE， ∴AD=BE． （2）∠AEB＝90°；AE=2CM+BE；理由如下： ∵△ACB 和△DCE 均为等腰直角三角形，∠ACB =∠DCE= 90°， ∴AC = BC， CD = CE， ∠ACB =∠DCB =∠DCE－∠DCB， 即∠ACD = ∠BCE， ∴△ACD≌△BCE， ∴AD = BE，∠BEC = ∠ADC=135°． ∴∠AEB =∠BEC－∠CED =135°－ 45°= 90°． 在等腰直角△DCE 中，CM 为斜边 DE 上的高， ∴CM =DM= ME，∴DE = 2CM． ∴AE = DE+AD=2CM+BE． 9．（ 2020·广东龙岗初二期末）如图，已知 ABC 为等边三角形，点 D、E 分别在 BC、AC 边上，且 AE=CD，AD 与 BE 相 交于点 F． （1）求证：BE=AD； （2）求∠BFD 的度数． 【答案】（1）见解析；（2）60° 【解析】解：（1）∵△ABC 是等边三角形， ∴AB=AC，∠BAC=∠C=60°， 又∵AE=CD， ∴△ABE≌△CAD（SAS）， ∴BE=AD； （2）∵△ABE≌△CAD， ∴∠ABE=∠CAD， ∴∠BFD=∠ABE+∠BAD=∠CAD+∠BAD=∠BAC=60°． 10．（ 2020·江西广丰初一期末）在同一平面内，将两块正三角形的纸板的两个顶点重合在一起． （1）如图 1 重叠部分∠AOD=30°，求∠COB 的大小； （2）如图 2 重叠部分∠AOD=15°，求∠COB 的大小； （3）如图 3，若两图形除 O 外没有重叠，∠AOD=10°，求∠COB 的大小； （4）求∠AOD 和∠COB 的数量关系． 【答案】（1）∠COB=90°；（ 2）∠COB=105°；（ 3）∠COB=130°；（ 4）①当∠AOD 是两个角的重叠的角，∠COB=120°-∠AOD； ②当∠AOD 是两个角的相离时的角，且小于或等于 60°，∠COB=120°+∠AOD；③当∠AOD 是两个角的相离时的角，且大于 60°，∠COB=240°-∠AOD． 【解析】解：（1）∵△COD 和△AOB 为两块正三角形 ∴∠COD=∠AOB=60° ∴∠COB=∠COD+∠AOB －∠AOD=60°＋60°－30°=90°； （2）同理∠COB=∠COD+∠AOB －∠AOD=60°＋60°－15°=105° （3）∠COB=∠COD＋∠AOB +∠AOD =60°+60°+10°=130°； （4）①当∠AOD 是两个角的重叠的角， 那么∠COB=120°－∠AOD； ②当∠AOD 是两个角的相离时的角，且小于或等于 60°， 那么∠COB=120°+∠AOD； ③当∠AOD 是两个角的相离时的角，且大于 60°， 那么∠COB=360°-(120°+∠AOD)=240°－∠AOD． 11．（ 2020·陕西西安初一期末）（2020•锦州模拟）问题情境：已知，在等边△ABC 中，∠BAC 与∠ACB 的角平分线交于点 O， 点 M、N 分别在直线 AC，AB 上，且∠MON＝60°，猜想 CM、MN、AN 三者之间的数量关系． 方法感悟：小芳的思考过程是在 CM 上取一点，构造全等三角形，从而解决问题； 小丽的思考过程是在 AB 取一点，构造全等三角形，从而解决问题； 问题解决：（1）如图 1，M、N 分别在边 AC，AB 上时，探索 CM、MN、AN 三者之间的数量关系，并证明； （2）如图 2，M 在边 AC 上，点 N 在 BA 的延长线上时，请你在图 2 中补全图形，标出相应字母，探索 CM、MN、AN 三者 之间的数量关系，并证明． 【答案】（1）CM＝AN+MN，详见解析；（2）CM＝MN﹣AN，详见解析 【解析】解：（1）CM＝AN+MN， 理由如下：在 AC 上截取 CD＝AN，连接 OD， ∵△ABC 为等边三角形，∠BAC 与∠ACB 的角平分线交于点 O， ∴∠OAC＝∠OCA＝30°， ∴OA＝OC， 在△CDO 和△ANO 中， OCOA OCDOAN CDAN      ， ∴△CDO≌△ANO（SAS） ∴OD＝ON，∠COD＝∠AON， ∵∠MON＝60°， ∴∠COD+∠AOM＝60°， ∵∠AOC＝120°， ∴∠DOM＝60°， 在△DMO 和△NMO 中， ODON DOMNOM OMOM      ， ∴△DMO≌△NMO， ∴DM＝MN， ∴CM＝CD+DM＝AN+MN； （2）补全图形如图 2 所示： CM＝MN﹣AN， 理由如下：在 AC 延长线上截取 CD＝AN，连接 OD， 在△CDO 和△ANO 中， 150 CDAN OCDOAN OCOA     ， ∴△CDO≌△ANO（SAS） ∴OD＝ON，∠COD＝∠AON， ∴∠DOM＝∠NOM， 在△DMO 和△NMO 中， OD ON DOM NOM OM OM       ， ∴△DMO≌△NMO（SAS） ∴MN＝DM， ∴CM＝DM﹣CD＝MN﹣AN． 考点 5：等边三角形的判定 典例：（2018·山西吕梁初二期末）问题情景：数学课上，老师布置了这样一道题目，如图 1，△ABC 是等边三角形，点 D 是 BC 的中点，且满足∠ADE＝60°，DE 交等边三角形外角平分线于点 E．试探究 AD 与 DE 的数量关系． 操作发现：（1）小明同学过点 D 作 DF∥AC 交 AB 于 F，通过构造全等三角形经过推理论证就可以解决问题，请您按照小明 同学的方法确定 AD 与 DE 的数量关系，并进行证明． 类比探究：（2）如图 2，当点 D 是线段 BC 上任意一点(除 B、C 外)，其他条件不变，试猜想 AD 与 DE 之间的数量关系，并 证明你的结论． 拓展应用：（3）当点 D 在线段 BC 的延长线上，且满足 CD＝BC，在图 3 中补全图形，直接判断△ADE 的形状(不要求证明)． 【答案】（1）AD＝DE，见解析；（2）AD＝DE，见解析；（3）见解析，△ADE 是等边三角形， 【解析】（1）如下图，数量关系：AD＝DE. 证明：∵ ABC 是等边三角形 ∴AB＝BC， 60B BAC BCA   ＝ ＝ ＝ ∵DF∥AC ∴ BFD BAC＝ ，∠BDF＝∠BCA ∴ 60BBFDBDF＝ ＝ ＝ ∴ B D F 是等边三角形， 120AFD＝ ∴DF＝BD ∵点 D 是 BC 的中点 ∴BD＝CD ∴DF＝CD ∵CE 是等边 ABC 的外角平分线 ∴ 120DCE AFD  ＝ ＝ ∵ 是等边三角形，点 D 是 BC 的中点 ∴AD⊥BC ∴ 90A D C＝ ∵ 60BDF ADE  ＝ ＝ ∴ 30ADF EDC  ＝ ＝ 在 ADF 与 E D C 中 AFD ECD DF CD ADF EDC    ＝ ＝ ＝ ∴ ()ADFEDCASA≌ ∴AD＝DE； （2）结论：AD＝DE. 证明：如下图，过点 D 作 DF∥AC，交 AB 于 F ∵ 是等边三角形 ∴AB＝BC， 60B BAC BCA   ＝ ＝ ＝ ∵DF∥AC ∴ BFD BAC BDF BCA   ＝ ， ＝ ∴ 60BBFDBDF＝ ＝ ＝ ∴ B D F 是等边三角形， 120AFD＝ ∴BF＝BD ∴AF＝DC ∵CE 是等边 ABC 的外角平分线 ∴ 120DCE AFD  ＝ ＝ ∵∠ADC 是 ABD 的外角 ∴ 60ADC B FAD FAD    ＝ ＋ ＝ ＋ ∵ 60ADC ADE CDE CDE    ＝ ＋ ＝ ＋ ∴∠FAD＝∠CDE 在 AFD 与 DCE 中 AFDDCE AFCD FADEDC    ＝ ＝ ＝ ∴ ()AFDDCEASA≌ ∴AD＝DE； （3）如下图， ADE 是等边三角形. 证明：∵ BCCD ∴ ACCD ∵CE 平分 ACD ∴CE 垂直平分 AD ∴AE=DE ∵ 60ADE ∴ 是等边三角形. 方法或规律点拨 本题主要考查了等边三角形的性质及判定，三角形全等的判定及性质，平行线的性质，垂直平分线的性质等相关内容，熟练 掌握三角形综合解决方法是解决本题的关键. 巩固练习 1．（ 2020·山东广饶初一期末）如图，在四边形 ABCD 中，对角线 AC 与 BD 相交于点 E，若 AC 平分∠DAB，且 AB=AC， AC=AD，有四个结论：①AC⊥BD；②BC=DC；③△ABC≌△ADC；④△ABD 是等边三角形．其中正确的是( ) A．①②③ B．①②④ C．②③④ D．①③④ 【答案】A 【解析】①∵AB=AC，AC=AD， ∴△ABD 是等腰三角形， ∵AC 平分∠DAB， ∴AC⊥BD，故①正确； ②∵AC⊥BD，BE=DE， ∴点 C 在 BD 的线段垂直平分线上， ∴BC=DC，故②正确； ③∵AB=AC，AC=AD，BC=CD， ∴△ABC≌△ADC，故③正确； ④∵∠BAD 不一定等于 60°， ∴△ABD 不一定是正三角形，故④错误． 所以正确结论有①②③，故选 A． 2．（ 2019·山东肥城初二开学考试）如图，D、E、F 分别是等边△ABC 各边上的点，且 AD=BE=CF，则△DEF 的形状是（ ）． A．等边三角形 B．腰和底边不相等的等腰三角形 C．直角三角形 D．不等边三角形 【答案】A 【解析】∵△ABC 为等边三角形，且 AD=BE=CF， ∴AE=BF=CD， 又∵∠A=∠B=∠C=60°， ∴△ADE≌△BEF≌△CFD（SAS）， ∴DF=ED=EF， ∴△DEF 是等边三角形， 故选 A. 3．（ 2019·湖南长沙初二期中）已知，如图，等腰△ABC，AB＝AC，∠BAC＝120°，AD⊥BC 于点 D，点 P 是 BA 延长线上 一点，点 O 是线段 AD 上一点，OP＝OC，下列结论：①AC 平分∠PAD；②∠APO＝∠DCO；③△OPC 是等边三角形；④AC ＝AO+AP；其中正确的序号是（ ） A．①③④ B．②③ C．①②④ D．①③ 【答案】A 【解析】解：①∵AB＝AC，∠BAC＝120°，AD⊥BC； ∴∠CAD＝ 1 2 ∠BAC＝60°，∠PAC＝180°﹣∠CAB＝60°， ∴∠PAC＝∠DAC， ∴AC 平分∠PAD，故①正确； ②由①知：∠APO＝∠ABO，∠DCO＝∠DBO， ∵点 O 是线段 AD 上一点， ∴∠ABO 与∠DBO 不一定相等，则∠APO 与∠DCO 不一定相等， 故②不正确； ③∵∠APC+∠DCP+∠PBC＝180°， ∴∠APC+∠DCP＝150°， ∵∠APO+∠DCO＝30°， ∴∠OPC+∠OCP＝120°， ∴∠POC＝180°﹣（∠OPC+∠OCP）＝60°， ∵OP＝OC， ∴△OPC 是等边三角形； 故③正确； ④如图，在 AC 上截取 AE＝PA， ∵∠PAE＝180°﹣∠BAC＝60°， ∴△APE 是等边三角形， ∴∠PEA＝∠APE＝60°，PE＝PA， ∴∠APO+∠OPE＝60°， ∵∠OPE+∠CPE＝∠CPO＝60°， ∴∠APO＝∠CPE， ∵OP＝CP， 在△OPA 和△CPE 中， PAPE APOCPE OPCP      ， ∴△OPA≌△CPE（SAS）， ∴AO＝CE， ∴AC＝AE+CE＝AO+AP； 故④正确． 故选：A． 4．（ 2019·北京师大附中初二期中）如图，∠AOB=120°，OP 平分∠AOB，且 OP=2.若点 M，N 分别在 OA，OB 上，且△PMN 为等边三角形，则满足上述条件的△PMN 有（ ） A．1 个 B．2 个 C．3 个 D．3 个以上 【答案】D 【解析】解：如图在 OA、OB 上截取 OE=OF=OP，作∠MPN=60°． ∵OP 平分∠AOB， ∴∠EOP=∠POF=60°， ∵OP=OE=OF， ∴△OPE，△OPF 是等边三角形， ∴EP=OP，∠EPO=∠OEP=∠PON=∠MPN=60°， ∴∠EPM=∠OPN， 在△PEM 和△PON 中， PEM PON PE PO EPM OPN    ＝ ＝ ＝ ， ∴△PEM≌△PON． ∴PM=PN，∵∠MPN=60°， ∴△PNM 是等边三角形， ∴只要∠MPN=60°，△PMN 就是等边三角形， 故这样的三角形有无数个． 故选 D． 5．（ 2019·东安县舜德学校初二期中）如图所示，E 是等边 ABC 中 AC 边上的点， 1= 2，BE CD ， 则对 ADE 的形状判断最准确的是( ) A．等腰三角形 B．等边三角形 C．不等边三角形 D．不能确定形状 【答案】B 【解析】解：判断△ADE 是等边三角形 理由如下：∵△ABC 是全等三角形， ∴AB＝AC，∠BAC＝60º, 在△ABE 和△ACD 中， 12 ABAC BECD    ＝ ＝ ＝ ∴△ABE≌△ACD（SAS）， ∴AE＝AD，∠CAD＝∠BAC＝60º， ∴△ADE 是等边三角形 故选：B 6．（ 2019·山东曹县）如图， ABC 为等边三角形， D 为 BC 延长线上一点，CE=BD， CE 平分 A C D ，下列结论:(1) BACDAE  ；(2) AEAD ；(3) ADE 是等边三角形，其中正确的个数为( ) A．0 个 B．1 个 C．2 个 D．3 个 【答案】D 【解析】 ABC 是等边三角形， A B A C ， 60BACBACB   ， 120A C D   ， CE 平分 A C D ， 1 602ACEACD  ， A C E B   ， 在 ABD△ 和 A C E△ 中 A B A C B A CE B D CE        ()ABDACESAS ， AD AE ，故（2）正确； ∴ C A E B A D   ∴ =60DAE BAC    ，故（1）正确； ∴ ADE 是等边三角形，故（3）正确． ∴正确有结论有 3 个． 故选：D． 7．（ 2020·广西初三三模）如图， RtABC 中， ACB=90，AC=CB=42 ， BAD=ADE=60 ， A D = 5 ， CE 平分 A C B ， DE 与 相交于点 E ，则 的长等于_____. 【答案】3 【解析】如图，延长 CE、DE，分别交 AB 于 G、H， ∵∠BAD=∠ADE=60°， ∴△ADH 是等边三角形， ∴DH=AD=AH=5，∠DHA=60°， ∵AC=BC，CE 平分∠ACB，∠ACB=90°， ∴AB= 22AC CB =8，AG= 1 2 AB=4，CG⊥AB， ∴GH=AH=AG=5-4=1， ∵∠DHA=60°， ∴∠GEH=30°， ∴EH=2GH=2 ∴DE=DH-EH=5=2=3. 故答案为 3 8．（ 2019·广西兴宾初二期中）如图，在△ABC 中，AB=AC，AH⊥BC，垂足为 H，D 为直线 BC 上一动点(不与点 B、C 重合)， 在 AD 的右侧作△ADE，使得 AE=AD，∠DAE=∠BAC，连接 CE． （1）求证：BD=CE； （2）若点 D 在线段 BC 上，问点 D 运动到何处时，AC⊥DE？请说明理由； （3）当 CE∥AB 时，若△ABD 中最小角为 20°，试探究∠ADB 的度数．(直接写出结果，无需写出求解过程) 【答案】（1）证明见解析；（2）当点 D 运动到 BC 中点(H 点)时，AC⊥DE．理由见解析；（3）∠ADB 的度数为 20°或 40°或 100°． 【解析】证明：（1）如图 1． ∵∠DAE=∠BAC ∴∠BAD=∠CAE 在△BAD 和△CAE 中， AB AC BAD CAE AD AE    ＝ ＝ ＝ ， ∴△BAD≌△CAE(SAS)， ∴BD=CE． （2）当点 D 运动到 BC 中点(H 点)时，AC⊥DE 理由是：如图 2． ∵AB=AC，AH⊥BC ∴∠BAH=∠CAH ∵∠BAH=∠CAE， ∴∠CAH=∠CAE ∵AH=AE， ∴AC⊥DE． （3）∠ADB 的度数为 20°或 40°或 100°． 理由如下： ①如图 3 中，当点 D 在 CB 的延长线上时， ∵CE∥AB， ∴∠BAE=∠AEC，∠BCE=∠ABC． ∵△DAB≌△EAC， ∴∠ADB=∠AEC，∠ABD=∠ACE， ∴∠BAC=∠BAE+∠EAC=∠AEC+∠EAC=180°-∠ACE=180°-∠ABD=∠ABC=∠ACB，∴△ABC 是等边三角形， ∴∠ABC=60° ∵△ABD 中的最小角是∠BAD=20°， 则∠ADB=∠ABC-∠BAD=40°． ②当点 D 在线段 BC 上时，最小角只能是∠DAB=20°， 同理可得：∠ADB=180°-20°-60°=100°． ③当点 D 在 BC 延长线上时，最小角只能是∠ADB=20°， 综上所述：满足条件的∠ABD 的值为 20°或 40°或 100°． 9．（ 2020·佛山市南海区桂城街道映月中学初二月考）如图，在△ABC 中，AD 是 BC 边上的高，BE 平分∠ABC 交 AC 边于 E， 两线相交于 F 点． （1）若∠BAC=60°，∠C=70°，求∠AFB 的大小； （2）若 D 是 BC 的中点，∠ABE=30°，求证：△ABC 是等边三角形． 【答案】（1）115°；（ 2）证明见解析 【解析】（1）∵∠BAC=60°，∠C=70°， ∴∠ABC= 180°﹣60°﹣70°=50°， ∵BE 平分∠ABC， ∴∠FBD= 1 2 ∠ABC=25°， ∵AD⊥BC， ∴∠BDF=90°， ∴∠AFB=∠FBD+∠BDF=115°． （2）证明：∵∠ABE=30°，BE 平分∠ABC， ∴∠ABC=60°， ∵BD=DC，AD⊥BC， ∴AB=AC， ∴△ABC 是等边三角形． 考点 6：含 30°锐角三角函数的直角三角形 典例：（2020·广西东兰初二期末） 如图，已知 ABC 为等边三角形，AE=CD, AD , BE 相交于点 F, BQAD 于点 Q． （1）求证： ADC ≌ BEA ； （2）若 4, 1FQ EF，求 AD 的长． 【答案】（1）证明见解析；（2）AD=9． 【解析】（1）证明：∵△ABC 为等边三角形， ∴AB=CA，∠BAE=∠C=60°， 在△AEB 与△CDA 中， A B CA B A E C A E CD        ， ∴△AEB≌△CDA（SAS）， （2）由（1）可知 A D C ≌ BEA ， ∴ ABFDAC  ,AD=BE 又 60BFQ=ABF+ BAF=DAC+ BAF= BQAD  9030FBQBFQ , BF=2FQ=8， ∴BE=BF+EF=8+1=9 ∴AD=9 方法或规律点拨 本题考查了全等三角形的判定与性质、含 30 度角的直角三角形，在判定三角形全等时，关键是选择恰当的判定条件． 巩固练习 1．（ 2020·甘肃兰州初二期末）如图，在 ABC中， ABAC10， BAC 120  ，AD 是 的中线，AE 是 BAD 的角平分线， DF / /AB交 AE 的延长线于点 F，则 DF 的长是 ( ) A．2 B．4 C．5 D． 5 2 【答案】C 【解析】∵AB=AC=10，∠BAC=120°，AD 是中线， ∴∠ABD=∠ACD= 1 2 （180°-120°）=30°，AD⊥BC， ∴AD= AB=5， ∵DF//AB， ∴∠DFA=∠BAF， ∵AF 是∠BAD 的角平分线， ∴∠BAF=∠DAF， ∴∠DAF=∠DFA， ∴DF=AD=5. 故选 C. 2．（ 2020·内蒙古杭锦后旗初二期末）如图，∠AOB＝150°，OC 平分∠AOB，P 为 OC 上一点，PD∥OA 交 OB 于点 D，PE⊥ OA 于点 E．若 OD＝4，则 PE 的长为（ ） A．2 B．2.5 C．3 D．4 【答案】A 【解析】解：∵PD∥OA，∠AOB=150° ∴∠PDO+∠AOB=180° ∴∠PDO=30° 过 O 作 OF⊥PD 于 F ∵OD=4 ∴OF= 1 2 ×OD=2 ∵PE⊥OA ∴FO=PE=2. 故选 A. 3．（ 2020·广西防城港初二期中）如图 5，一棵大树在一次强台风中于离地面 5 米处折断倒下，倒下部分与地面成 30°夹角， 这棵大树在折断前的高度为（ ） A．10 米 B．15 米 C．25 米 D．30 米 【答案】B 【解析】解：如图，在 Rt△ABC 中，∵∠ABC=30°， ∴AB=2AC， 而 CA=5 米， ∴AB=10 米， ∴AB+AC=15 米． 所以这棵大树在折断前的高度为 15 米． 故选 B． 4．（ 2020·山东岚山初二期末）如图，边长为 12 的等边三角形 ABC 中，E 是高 AD 上的一个动点，连结 CE，将线段 CE 绕点 C 逆时针旋转 60°得到 CF，连结 DF．则在点 E 运动过程中，线段 DF 长度的最小值是__________． 【答案】3 【解析】解：如图，取 AC 的中点 G，连接 EG， ∴ 1 2AG CG AC ． ∵旋转角为 60°， ∴∠ECD+∠DCF=60°， 又∵∠ECD+∠GCE=∠ACB=60°，∠ECD=∠ECD， ∴∠DCF=∠GCE， ∵AD 是等边△ABC 底边 BC 的高，也是中线， ∴ 1 2C D B C ， ∴CD=CG， 又∵CE 旋转到 CF， ∴CE=CF， 在△DCF 和△GCE 中， CECF DCFGCE CDCG      ， ∴△DCF≌△GCE（SAS）， ∴DF=EG， 根据垂线段最短，EG⊥AD 时，EG 最短，即 DF 最短， 此时 1 60302CAD  ， 1112622AGAC ， 116322EGAG ， ∴DF=EG=3． 故答案为：3． 5．（ 2020·湖南渌口初三其他）如图，△ABC 中，∠C＝90°，AC＝3，∠B＝30°，点 P 是 BC 边上的动点，则在①3.6②4，③ 5.5，④7，这四个数中 AP 长不可能是_____ （填序号） 【答案】④ 【解析】根据垂线段最短，可知 AP 的长不可小于 3； ∵△ABC 中，∠C＝90°，AC＝3，∠B＝30°， ∴AB＝6， ∴AP 的长不能大于 6． 故答案为：④ 6．（ 2020·广东南海初二期末）如图，在 Rt△ABC 中，∠C＝90°，∠ABC＝30°，AB＝10，将 △ABC 沿 CB 方向向右平移得到△DEF．若 四边形 ABED 的面积为 20，则平移距离为___________． 【答案】4 【解析】解：在 Rt△ABC 中，∵∠ABC=30°， ∴AC= 1 2 AB=5， ∵△ABC 沿 CB 向右平移得到△DEF， ∴AD=BE，AD // BE， ∴四边形 ABED 为平行四边形， ∵四边形 ABED 的面积等于 20， ∴AC•BE=20，即 5BE=20， ∴BE=4，即平移距离等于 4． 故答案为：4． 7．（ 2020·贵州铜仁伟才学校初二期中）如图，△ABC 中，∠C=90°，∠ABC=60°，BD 平分∠ABC，若 AD=6，则 CD=_______. 【答案】3 【解析】∵∠C=90°，∠ABC=60°， ∴∠A=30°． ∵BD 平分∠ABC， ∴∠CBD=∠ABD=∠A=30°， ∴BD=AD=6， ∴CD= 1 2 BD=6× =3． 故答案为 3． 8．（ 2020·山西寿阳初二期中）如图，将一幅三角尺如图所示叠放在一起，若 AB=24cm，则阴影部分的面积是__． 【答案】72cm2 【解析】∵∠B=30°，∠ACB=90°，AB=24cm， ∴AC= 1 2 AB=12cm． 由题意可知 BC∥ED， ∴∠AFC=∠ADE=45°， ∴AC=CF=12cm． 故 S△ACF= ×12×12=72（cm2）． 故答案为：72cm2． 9．（ 2020·广东高州初二期中）如图，已知在 ABC 中，ABAC ，D 为 BC 边的中点，过点 作 DE AB ，DF AC ， 垂足分别为 E ， F . （1）求证： DE DF ； （2）若 60A   ， 1BE  ，求 ABC 的周长. 【答案】（1）见解析；（2）12 【解析】（1）证明: ∵DE⊥AB,DF⊥A， ∴∠BED=∠CFD=90°， ∵AB=AC， ∴∠C=∠B， ∵D 是 BC 的中点， ∴.BD=CD， 在△BED 和△CFD 中, BEDCFD BC BDCD      , ∴△BED≌△CFD， ∴DE=DF ； （2）解：∵AB=AC, ∠A=60°， ∴△ABC 为等边三角形， .∴∠B=60°， ∵∠BED=90°， ∴∠BDE=30°， ∴ 1 2BEBD ， ∵BE=1， ∴BD=2， ∴BC=2BD=4. ∴△ABC 的周长为 12. 10．（ 2020·甘肃省武威市第十中学初三三模）如图，已知∠AOB＝60°，点 P 在边 OA 上，OP＝12，点 M，N 在边 OB 上， PM＝PN，若 MN＝2，求 OM 的长． 【答案】OM＝5． 【解析】解：过 P 作 PD⊥OB，交 OB 于点 D， 在 Rt△OPD 中，∠AOB=60º，OP＝12，∴OD＝ 1 2 OP=6， ∵PM＝PN，PD⊥MN，MN＝2， ∴MD＝ND＝ MN＝1， ∴OM＝OD－MD＝6－1＝5． 考点 7：最短路径问题 典例：（2019·湖北十堰初二期中）如图，在平面直角坐标系中 （1）做出△ABC 关于 y 轴对称的 1 1 1A B C ,并求出 三个顶点的坐标； （2）计算△ABC 的面积； （3）在 x 轴上画点 P，使 PA+PC 最小． 【答案】（1） 111(1,2),(3,1),(4,3)ABC ；（ 2）2.5；（ 3）见解析 【解析】解：（1）如图所示： （2）如图，将 ABC 补成矩形 E F D C ，则 1AE  ， 3EC  ， 1AF  ， 2BF  ， 1BD  ， 2CD  ， 2EF  ， 3FD  ， ABCAECAFBBCDEFDCSSSSS 矩 1 1 1 2 2 2EF FD AE EC AF BF BD CD        11123131212222 61.511 2.5 （3）如图所示 方法或规律点拨 本题考查了作坐标系中的对称图形，利用构造法来求三角形面积和将军饮马的问题，熟练掌握相关知识点是解决本题的关键． 巩固练习 1．（ 2020·山东槐荫初一期末）某平原有一条很直的小河和两个村庄，要在此小河边的某处修建一个水泵站向这两个村庄供水. 某同学用直线（虛线） l 表示小河， ,PQ两点表示村庄，线段（实线）表示铺设的管道，画出了如下四个示意图，则所需管 道最短的是（ ）. A． B． C． D． 【答案】C 【解析】根据题意，所需管道最短，应过点 P 或点 Q 作对称点，再连接另一点，与直线 l 的交点即为水泵站 M，故选项 A、 B、D 均错误，选项 C 正确， 故选：C. 2．（ 2020·河南内黄初二期末）如图，在直角坐标系中，点 A、B 的坐标分别为（1，4）和（3，0），点 C 是 y 轴上的一个动 点，且 A、B、C 三点不在同一条直线上，当△ABC 的周长最小时，点 C 的坐标是 A．（ 0，0） B．（ 0，1） C．（ 0，2） D．（ 0，3） 【答案】D 【解析】解：作 B 点关于 y 轴对称点 B′点，连接 AB′，交 y 轴于点 C′， 此时△ABC 的周长最小， ∵点 A、B 的坐标分别为（1，4）和（3，0）， ∴B′点坐标为：（-3，0），则 OB′=3 过点 A 作 AE 垂直 x 轴，则 AE=4，OE=1 则 B′E=4，即 B′E=AE，∴∠EB′A=∠B′AE， ∵C′O∥AE， ∴∠B′C′O=∠B′AE， ∴∠B′C′O=∠EB′A ∴B′O=C′O=3， ∴点 C′的坐标是（0，3），此时△ABC 的周长最小． 故选 D． 3．（ 2019·河南汝州初二期末）如图，等腰三角形 ABC 的底边 BC 长为 4 ，面积是16 ， 腰 AC 的垂直平分线 EF 分别交 ,AC AB 边于 ,EF点．若点 D 为 边的中点，点 M 为线段 EF 上一动点，则 CDM 周长的最小值为（ ） A． 6 B． 8 C． 10 D． 12 【答案】C 【解析】解：连接 AD， ∵△ABC 是等腰三角形，点 D 是 BC 边的中点， ∴AD⊥BC， ∴S△ABC= 1 2 BC•AD= ×4×AD=16，解得 AD=8， ∵EF 是线段 AC 的垂直平分线， ∴点 C 关于直线 EF 的对称点为点 A， ∴AD 的长为 CM+MD 的最小值， ∴△CDM 的周长最短=（CM+MD）+CD 1184821022ADBC 故选：C． 4．（ 2020·山东历下初一期末）如图，点 P 是∠AOB 内任意一点，OP＝8，M、N 分别是射线 OA 和 OB 上的动点，若△PMN 周长的最小值为 8，则∠AOB＝__________． 【答案】30° 【解析】解：分别作点 P 关于 OA、OB 的对称点 C、D，连接 CD，分别交 OA、OB 于点 M、N，连接 OC、OD、PM、PN、 MN，如图所示： ∵点 P 关于 OA 的对称点为 D，关于 OB 的对称点为 C， ∴PM=DM，OP=OD，∠DOA=∠POA； ∵点 P 关于 OB 的对称点为 C， ∴PN=CN，OP=OC，∠COB=∠POB， ∴OC=OP=OD，∠AOB= 1 2 ∠COD， ∵△PMN 周长的最小值是 8， ∴PM+PN+MN=8， ∴DM+CN+MN=8，即 CD=8=OP， ∴OC=OD=CD，即△OCD 是等边三角形， ∴∠COD=60°， ∴∠AOB=30°， 故答案为：30°． 5．（ 2020·山东历下初一期末）如图，AD 为等边△ABC 的高，E、F 分别为线段 AD、AC 上的动点，且 AE＝CF，当 BF＋CE 取得最小值时，∠AFB＝_______°． 【答案】105° 【解析】解：如图，作 CH⊥BC，且 CH＝BC，连接 BH 交 AD 于 M，连接 FH， ∵△ABC 是等边三角形，AD⊥BC， ∴AC＝BC，∠DAC＝30°， ∴AC＝CH， ∵∠BCH＝90°，∠ACB＝60°， ∴∠ACH＝90°−60°＝30°， ∴∠DAC＝∠ACH＝30°， ∵AE＝CF， ∴△AEC≌△CFH， ∴CE＝FH，BF＋CE＝BF＋FH， ∴当 F 为 AC 与 BH 的交点时，BF＋CE 的值最小， 此时∠FBC＝45°，∠FCB＝60°， ∴∠AFB＝105°， 故答案为：105°. 6．（ 2020·武汉市梅苑学校初二期中）如图，在 Rt ABC 中，AC⊥BC，若 AC＝7，BC＝24，AB＝25，将 Rt 折叠， 使得点 C 恰好落在 AB 边的点 E 处，折痕为 AD，点 P 为 AD 上一动点，则 PEB△ 的周长最小值为___________． 【答案】42 【解析】解：连接 CP， 由于折叠可得：点 C 和点 E 关于 AD 对称， ∴CP=EP， 在△PEB 中，BE 固定不变， PE 和 PB 随点 P 的位置变化， ∴当点 P 在点 D 的位置上时， PC+PB 最小，即 PE+PB 最小， ∵AC=7，BC＝24，AB＝25， ∴AE=7，BE=18， ∴PE+PB 的最小值为 CD+BD=BC=24， ∴△PEB 的周长最小值为 PE+PB+BE=24+18=42. 故答案为：42. 7．（ 2020·沈阳市第一二七中学初一期中）如图，等边△ABC 中，BD⊥AC 于点 D，AD＝3.5cm，点 P、Q 分别为 AB、AD 上 的两个定点且 BP＝AQ＝2cm，若在 BD 上有一动点 E 使 PE＋QE 最短，则 PE＋QE 的最小值为_____cm 【答案】5 【解析】 如图，过 BD 作 P 的对称点 P  ,连接 P ，Q ，Q 与 BD 交于一点 E，再连接 PE，此时 PE＋QE 最小. ∵ 与 P 关于 BD 对称， ∴PE= E，BP=B =2cm， ∴PE＋QE= Q ， 又∵等边△ABC 中，BD⊥AC 于点 D，AD＝3.5cm， ∴AC=BC=AB=7cm， ∵BP＝AQ＝2cm， ∴QC=5cm， ∵B =2cm， ∴C =5cm， ∴△Q C 为等边三角形， ∴Q =5cm. ∴PE＋QE=5cm. 所以答案为 5. 8．（ 2020·上饶市广信区第七中学初二月考）如图，等腰三角形 A B C 的底边 BC 长为 6，面积是 36，腰 AC 的垂直平分线 EF 分别交 ， AB 边于 E ， F 点，若点 D 为 边的中点，点 M 为线段 上一动点，则 C D M 周长的最小值____． 【答案】15 【解析】解：连接 AD， ∵△ABC 是等腰三角形，点 D 是 BC 边的中点， ∴AD⊥BC， ∴S△ABC= 1 2 BC•AD= ×6×AD=36，解得 AD=12， ∵EF 是线段 AC 的垂直平分线， ∴点 C 关于直线 EF 的对称点为点 A， ∴AD 的长为 CM+MD 的最小值， ∴△CDM 的周长最短=（CM+MD）+CD=AD+ BC=12+ ×6=12+3=15． 故答案为：15． 9．（ 2020·重庆南岸初一期末）如图所示，在街道 l 的同一侧，有两个居民区 A，B，两个居民区门口到街道的距离分别为 AC， BD．现准备在街道 旁设置一个快递中转站． （1）如果设置的快递中转站到 A，B 两个小区的距离相等，如图 1，当∠A=∠BPD 时，请说明 AC+BD=CD 的理由； （2）如果设置的快递中转站到 A，B 两个小区的距离之和最短，请在图 2 中作出点 P 的位置，连接 AP，BP，直接写出此时 ∠PAC 与∠PBD 的数量关系； （3）为了能错峰进行取送快递，决定设置的快递中转站到 A，B 两个小区的距离之差最大，请在图 3 中作出点 P 的位置，连 接 AP，BP，直接写出此时∠PAC 与∠PBD 的数量关系． 【答案】（1）理由见解析；（2）∠PAC=∠PBD；（ 3）∠PAC=∠PBD． 【解析】（1）∵ AC，BD 分别是点 A，B 到直线 l 的距离， ∴ ∠ACP=∠BDP=90°， 在△ACP 和△PDB 中， ACPPDB ADPB APBP      ， ∴ △ACP≌△PDB（AAS）， ∴ AC=PD，PC=BD， ∴CD=CP+PD=BD+AC； （2）如图 1 所示，∠A＝∠B， 理由：由作图知， AC＝ AC ， AA ⊥l， ∴∠A＝∠ A  A， ∵A ∥BD， ∴∠ ＝∠B， ∴∠A＝∠B； （3）如图 2 所示， ∵∠ACD＝∠BDC＝90°， ∴∠ACD＋∠BDC＝180°， ∴AC∥BD， ∴∠PAC＝∠PBD． 10．（ 2019·河南汝州初一期末）如图，在正方形网格中，每个小正方形的边长都为 1，网格中有两个格点 A、B 和直线 l ． （1）求作点 A 关于直线 的对称点 1A ； （2） P 为直线 上的点，连接 BP 、 AP ，求 ABP△ 周长的最小值． 【答案】（1）详见解析；（2）10 【解析】解：（1）如图所示 （2）连接 、 B 交直线 于点 ，连接 AB ， ，则 1AP A P ．根据两点之间线段最短可知 AP BP 的最小值 1 6AB ，即 的周长的最小值 6 4 10   ．