人教版八年级上册数学同步练习课件-第11章-数学活动——平面镶嵌 17页

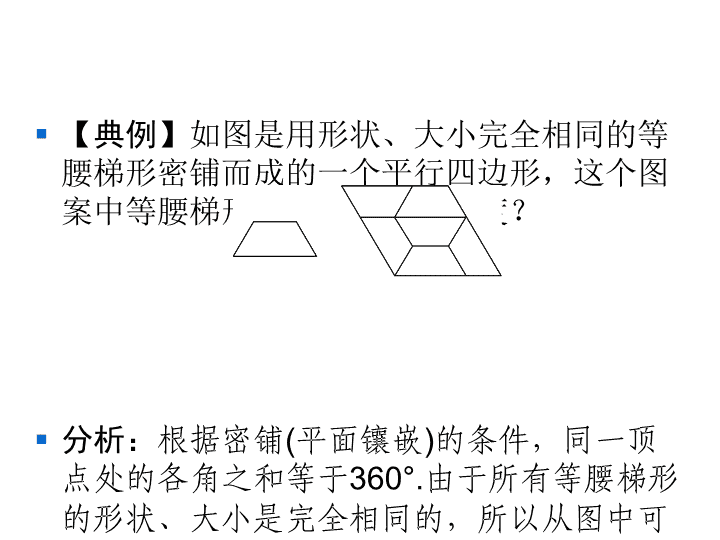
第十一章　三角形 数学活动——平面镶嵌(第三课时) § 知识点1　平面镶嵌问题 § 用一些不重叠摆放的多边形把平面的一部分 完全覆盖，通常把这类问题叫做用多边形覆 盖平面(或平面镶嵌)． § 知识点2　平面镶嵌的条件 § (1)拼接在同一个顶点处的各个角的和恰好等 于360°； § (2)相邻的多边形有公共边． § 注意：(1)能够进行平面镶嵌的同一种正多边 形只有：正三角形、正方形和正六边形； § (2)能够进行平面镶嵌的两种正多边形组合有： 正三角形与正方形，正三角形与正六边形， 正方形与正八边形等． 2 § 【典例】如图是用形状、大小完全相同的等 腰梯形密铺而成的一个平行四边形，这个图 案中等腰梯形的内角各是多少度？ § 分析：根据密铺(平面镶嵌)的条件，同一顶 点处的各角之和等于360°.由于所有等腰梯 形的形状、大小是完全相同的，所以从图中 可以看出，三个同样的钝角拼在了一起，所 以每个钝角是120°，锐角是60°. 3 § 解答：设等腰梯形的钝角度数为x. § 观察图案，得3x＝360°， § 解得x＝120°. § 所以锐角为180°－120°＝60°， § 所以等腰梯形的各内角分别为60°，120°， 120°，60°. § 点评：利用多边形进行平面镶嵌，满足顶点 处构成一个周角即可． 4 § 1．只用下列哪一种正多边形，可以进行平面 镶嵌(　　) § A．正五边形　　 B．正六边形　　 § C．正八边形　　 D．正十边形 § 2．在正三角形、正方形、正五边形和正六边 形四种图形中，能够单独铺满平面的有(　　) § A．4种　　 B．3种　　 § C．2种　　 D．1种 5 B 　 B § 3．为了美化城市，建设中的某小广场准备用 边长相等的正方形和正八边形两种地砖镶嵌 地面，在每一个顶点周围，正方形、正八边 形地砖的块数分别是(　　) § A．1,2　　 B．2,1　　 § C．2,3　　 D．3,2 § 解析：正方形的每个内角是90°，正八边形 的每个内角为180°－360°÷8＝ 135°.∵90°＋2×135°＝360°，∴正方 形、正八边形地砖的块数分别是1,2. § 4．在正三角形、正四边形、正五边形和正六 边形中不能单独密铺的是____________. 6 A 　 正五边形　 § 5．下面的图形，只通过平移方式就能进行平 面镶嵌(即平面密铺)的有__________.(写出 所有正确答案的序号) 7 ②③　 § 解析：①正三角形，虽然能平面镶嵌但是需 通过旋转操作，故错误；②正方形，每个内 角等于90°，通过平移就能进行平面镶嵌， 故正确；③长方形，每个内角等于90°，通 过平移就能进行平面镶嵌，故正确；④正五 边形，每个内角等于108°，不能平面镶嵌， 故错误． 8 § 6．用如图所示的图形作平面镶嵌，同一顶点 周围，该图形的个数为_________个． § 7．一幅图案在某个顶点处由三个边长相等的 正多边形镶嵌而成．其中的两个分别是正方 形和正六边形，求第三个正多边形的边数是 __________. § 解析：∵正方形的每个内角是90°，正六边 形的每个内角是120°，相加得210°， 360°－210°＝150°，∴第三个正多边形 的边数为：360°÷(180°－150°)＝12. 9 6　 12　 § 8．请你设计出一个用边长相等的正三角形和 正六边形进行平面镶嵌的图案？请画出来． § 解：如图所示． 10 § 9．下列美妙的图案中，是由正三角形、正方 形、正六边形、正八边形中的三种镶嵌而成 的为(　　) 11 D 　 12 B 　 § 11．一个边长为16 m的正方形展厅，准备用 边长分别为1 m和0.5 m的两种正方形地板砖 铺设地面．要求正中心一块是边长为1 m的 大地板砖，然后从内到外一圈小地板砖、一 圈大地板砖相间镶嵌(如图所示)，则铺好整 个展厅地面共需要边长为1 m的大地板砖 ___________块． 13 181　 解析：分层：正中心1块，第三层：1×3×4＝12(块)，第 五层：2×3×4＝24(块)，第七层3×3×4＝36(块)，第九层： 4×3×4＝48(块)，第十一层：5×3×4＝60(块)(此时边长为16 m)， 则铺好整个展厅地面共需要边长为1 m的大地板砖1＋12＋24＋36 ＋48＋60＝181(块)． § 12．用黑白两种正六边形地面瓷砖按如图所 示规律拼成若干图案，求第n个图案中白色地 面瓷砖的块数． § 解：由图知，第1个图案白色瓷砖的块数是6； 第2个图案白色瓷砖的块数是10＝6＋4；第3 个图案白色瓷砖的块数是14＝6＋4×2；…； 以此类推，第n个图案白色瓷砖的块数是6＋ 4(n－1)＝4n＋2. 14 § 13．一个正m边形恰好被正n边形围住(无重 叠，无间隙，如图所示的m＝4，n＝8的情 形)，按下列要求解答： § (1)当m＝10，n＝_________； § (2)用你学过的多边形的知识，说明第(1)题的 正确性． § 解：∵正十边形的每个内角为144°，正五 边形的每个内角为108°，∴144°＋ 2×108°＝360°，∴第(1)题中的n＝5是正 确的． 15 5　 § 14．黑色正三角形与白色正六边形的边长相 等，用它们镶嵌图案，方法如下：白色正六 边形分上下两行，上面一行的正六边形个数 比下面一行少一个，正六边形之间的空隙用 黑色的正三角形嵌满．按第1,2,3个图案(如图) 所示规律依次下去，则第n个图案中，黑色正 三角形和白色正六边形的个数分别是(　　) § A．n2＋n＋2,2n＋1　　 § B．2n＋2,2n＋1 § C．4n，n2－n＋3　　 § D．4n,2n＋1 16 D 　 § 解析：第1个图案中，黑色正三角形和白色正 六边形的个数分别是4,2×1＋1＝3；第2个 图案中，黑色正三角形和白色正六边形的个 数分别是2×4＝8,2×2＋1＝5；第3个图案 中，黑色正三角形和白色正六边形的个数分 别是3×4＝12,2×3＋1＝7；…，第n个图案 中，黑色正三角形和白色正六边形的个数分 别是4n,2n＋1. 17