河南省信阳市罗山县2020届九年级上学期期末质量监测数学试题 10页

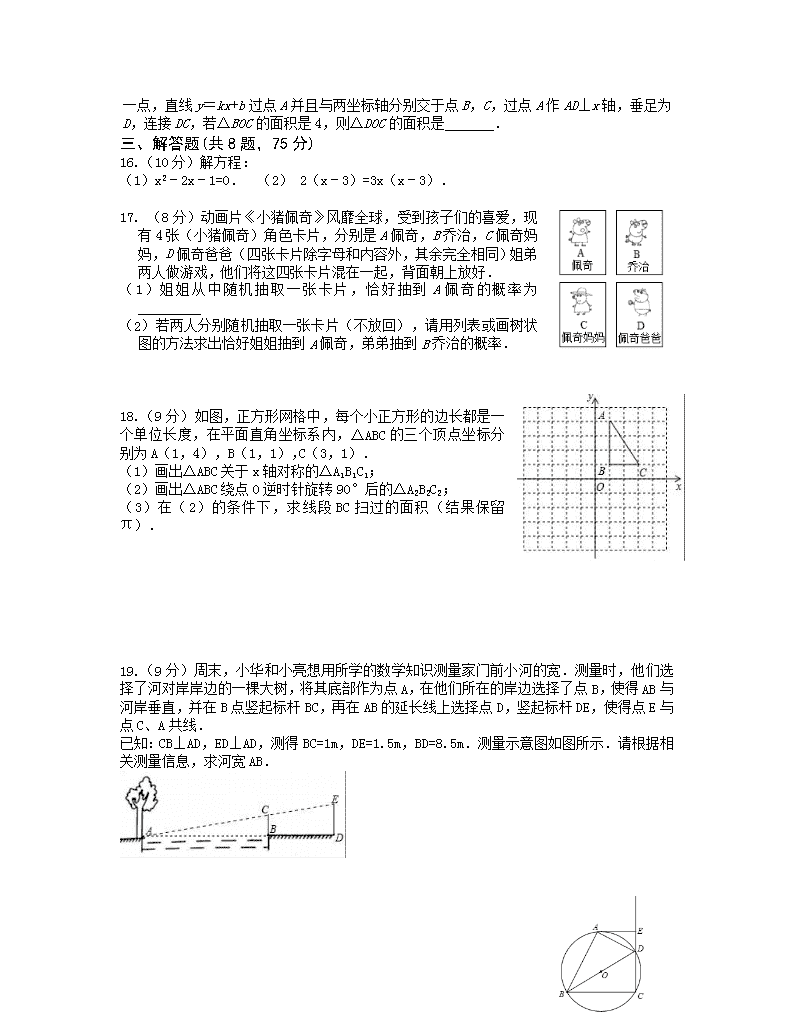
‎2019—2020学年度上期期末质量监测试卷 九年级数学 一． 选择题(每小题3分，共30分)‎ ‎1.抛物线y=3（x﹣2）2+5的顶点坐标是（　　）‎ A．（﹣2，5） B．（﹣2，﹣5） C．（2，5） D．（2，﹣5）‎ ‎2.某校九年级共有1、2、3、4四个班，现从这四个班中随机抽取两个班进行一场篮球比赛，则恰好抽到1班和2班的概率是（　　）‎ A． B． C． D．‎ ‎3.如图是用围棋棋子在6×6的正方形网格中摆出的图案，棋子的位置用有序数对表示，如A点为（5，1），若再摆一黑一白两枚棋子，使这9枚棋子组成的图案既是轴对称图形又是中心对称图形，则下列摆放正确的是（ ）‎ A.黑，白 B.黑，白 C.黑，白 D.黑，白 ‎ 3题图 4题图 5题图 ‎4.如图，在平面直角坐标系中，将△ABC绕A点逆时针旋转90°后，B点对应点的坐标为（ ）‎ A. B. C. D.‎ ‎5.如图，在三角形中，，，将三角形绕点按顺时针方向旋转到三角形的位置，使得点、、在一条直线上，那么旋转角等于（ ）‎ A.145° B. 70° C.125° D.55°‎ ‎6.宾馆有50间房供游客居住，当每间房每天定价为180元时，宾馆会住满；当每间房每天的定价每增加10元时，就会空闲一间房．如果有游客居住，宾馆需对居住的每间房每天支出20元的费用．当房价定为多少元时，宾馆当天的利润为10890元？设房价定为x元．则有（　　）‎ A．（180+x﹣20）（50﹣）=10890 B．（x﹣20）（50﹣）=10890‎ C．x（50﹣）﹣50×20=10890 D．（x+180）（50﹣）﹣50×20=10890‎ ‎7.如图，点B，C，D在⊙O上，若∠BCD＝130°，则∠BOD的度数是（　　）‎ A．50° B．60° C．80° D．100°‎ A B C D E F ‎ ‎ ‎ 7题图 8题图 9题图 ‎8.如图，在矩形中，在上，，交于，连结，则图中与 一定相似的三角形是（ ）‎ A． B． ‎ C． D．和 ‎ ‎9.如图，等腰直角△ABC中，AB=AC=8，以AB为直径的半圆O交斜边BC于D，则阴影部分面积为（结果保留π）（　　） ‎ A.24﹣4π B． 32﹣4π C． 32﹣8π D． 16‎ ‎10.如图，二次函数y=ax2+bx+c的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，2）与（0，3）之间（不包括这两点），对称轴为直线x=2．‎ 下列结论：①abc＜0；②9a+3b+c＞0；③若点M（，y1），点N（，y2）是函数图象上的两点，则y1＜y2；④﹣＜a＜﹣．‎ 其中正确结论有（　　）‎ A．1个  B．2个  C．3个  D．4个 二、选择题(每小题3分，共15分)‎ 11. 在一个布袋中装有四个完全相同的小球，它们分别写有“美”、“丽”、“罗”、“山”的文字．先从袋中摸出1个球后放回，混合均匀后再摸出1个球，求两次摸出的球上是含有“美”“丽”二字的概率为　 　.‎ 12. 关于x的一元二次方程kx2+3x﹣1＝0有实数根，则k的取值范围是k　 　‎ ‎13.已知A（﹣4，y1），B（﹣1，y2）,C(1,y3） 是反比例函数y=﹣图象上的两个点，把y1与y2、y3的的值用小于号连接表示为　 　．‎ ‎14.如图，在矩形ABCD中，E是边AB的中点，连接DE交对角线AC于点F，若AB=4，AD=3，则CF的长为　 　．‎ 15． 如图，点A是反比例函数y＝（x＞0）图象上 14题图 15题图 ‎ 一点，直线y＝kx+b过点A并且与两坐标轴分别交于点B，C，过点A作AD⊥x轴，垂足为 ‎ D，连接DC，若△BOC的面积是4，则△DOC的面积是　 　．‎ 三、解答题(共8题，75分)‎ ‎16.（10分）解方程：‎ ‎（1）x2﹣2x﹣1=0． （2） 2（x﹣3）=3x（x﹣3）．‎ ‎17. （8分）动画片《小猪佩奇》风靡全球，受到孩子们的喜爱，现有4张（小猪佩奇）角色卡片，分别是A佩奇，B乔治，C佩奇妈妈，D佩奇爸爸（四张卡片除字母和内容外，其余完全相同）姐弟两人做游戏，他们将这四张卡片混在一起，背面朝上放好．‎ ‎（1）姐姐从中随机抽取一张卡片，恰好抽到A佩奇的概率为_________‎ ‎（2）若两人分别随机抽取一张卡片（不放回），请用列表或画树状图的方法求出恰好姐姐抽到A佩奇，弟弟抽到B乔治的概率．‎ ‎18.（9分）如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系内，△ABC的三个顶点坐标分别为A（1，4），B（1，1），C（3，1）．‎ ‎（1）画出△ABC关于x轴对称的△A1B1C1；‎ ‎（2）画出△ABC绕点O逆时针旋转90°后的△A2B2C2；‎ ‎（3）在（2）的条件下，求线段BC扫过的面积（结果保留π）．‎ ‎19.（9分）周末，小华和小亮想用所学的数学知识测量家门前小河的宽．测量时，他们选择了河对岸岸边的一棵大树，将其底部作为点A，在他们所在的岸边选择了点B，使得AB与河岸垂直，并在B点竖起标杆BC，再在AB的延长线上选择点D，竖起标杆DE，使得点E与点C、A共线．‎ 已知：CB⊥AD，ED⊥AD，测得BC=1m，DE=1.5m，BD=8.5m．测量示意图如图所示．请根据相关测量信息，求河宽AB．‎ ‎[来源:学*科*网]‎ ‎20.如图，四边形ABCD内接于⊙O，BD是⊙O的直径，AE⊥CD于点E，DA平分∠BDE ‎（1）求证：AE是⊙O的切线；‎ ‎（2）若∠DBC=30°，DE=1cm，求BD的长；‎ ‎21．（9分）如图，A（4，3）是反比例函数y=在第一象限图象上一点，连接OA，过A作AB∥x轴，截取AB=OA（B在A右侧），连接OB，交反比例函数y=的图象于点P．‎ ‎（1）求反比例函数y=的表达式；‎ ‎（2）求点B的坐标；‎ ‎（3）求△OAP的面积．‎ ‎22．（9分）为积极响应新旧动能转换，提高公司经济效益，某科技公司近期研发出一种新型高科技设备，每台设备成本价为30万元，经过市场调研发现，每台售价为40万元时，年销售量为600台；每台售价为45万元时，年销售量为550台．假定该设备的年销售量y（单位：台）和销售单价x（单位：万元）成一次函数关系．‎ ‎（1）求年销售量y与销售单价x的函数关系式；‎ ‎（2）根据相关规定，此设备的销售单价不得高于70万元，如果该公司想获得10000万元的年利润，则该设备的销售单价应是多少万元？‎ ‎23.（11分）已知在平面直角坐标系中，抛物线y=-+bx+c与x轴相交于点A，B，与y轴相交于点C，直线y=x+4经过A，C两点，‎ ‎（1）求抛物线的表达式；‎ ‎（2）如果点P，Q在抛物线上（P点在对称轴左边），且PQ∥AO，PQ=2AO，求P，Q的坐标；‎ ‎（3）动点M在直线y=x+4上，且△ABC与△COM相似，求点M的坐标．‎ ‎[来源:学§科§网]‎ ‎2019—2020学年度上期期末质量监测试卷 九年级数学参考答案 一、选择题（每小题3分，共18分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7[来源:学科网ZXXK]‎ ‎8‎ ‎9‎ ‎10‎ 答案 C B D A C B D B A D 二、填空题（每小题3分，共27分）‎ 题号 ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ 答案 y3＜y1＜y2‎ ‎2 ﹣2‎ 三．解答题 ‎16.解方程（过程不唯一）‎ 解：（1）a=1，b=﹣2，c=﹣1，‎ ‎△=b2﹣4ac=4+4=8＞0，-------1分 方程有两个不相等的实数根，‎ x===1，-----4分 则x1=1+，x2=1﹣．-------5分 ‎　‎ (2) ‎ 2（x﹣3）=3x（x﹣3），‎ 移项得：2（x﹣3）﹣3x（x﹣3）=0，-----2分 整理得：（x﹣3）（2﹣3x）=0，----3分 x﹣3=0或2﹣3x=0，------4分 解得：x1=3或x2=．-------5分 ‎17.‎ ‎ ‎ ‎ --- -------3分 ‎ ----- -------7分 ‎ ------9分 九年级数学答案 第5页（共4页）‎ ‎18.解：（1）△ABC关于x轴对称的△A1B1C1如图所示；---3分 ‎（2）△ABC绕点O逆时针旋转90°后的△A2B2C2如图所示；-6分 ‎（3）BC扫过的面积=﹣=﹣‎ ‎=2π．--------9分 ‎19.解：∵BC∥DE，‎ ‎∴△ABC∽△ADE，-------3分[来源:学科网]‎ ‎∴=，------4分 ‎∴=，-----6分 ‎∴AB=17（m），----8分 经检验：AB=17是分式方程的解，‎ 答：河宽AB的长为17米．------9分 ‎20.（1）证明：连接OA，‎ ‎∵OA=OD， ∴∠OAD=∠ODA，-----1分 ‎∵DA平分∠EDB， ∴∠EDA=∠ODA，‎ ‎∴∠OAD=∠EDA，------3分 ‎∴OA∥CE， ∵AE⊥CD，‎ ‎∴OA⊥AE，-------4分 ‎∵OA是⊙O的半径，‎ ‎∴AE是⊙O的切线．-------5分 ‎（2）解：∵BD是⊙O的直径，‎ ‎∴∠BCD=∠BAD=90°，‎ ‎∵∠DBC=30°， ∴∠CDB=60°，‎ ‎∴∠EDA=∠ADB=（180°-60°）=60°，-----6分 ‎∵AE⊥CD， ∴∠AEC=90°， ∴∠EAD=30°， ∵DE=1cm，‎ ‎∴AD=2DE=2cm，--------------7分 ‎∵∠BAD=90°，∠ADB=60°， ∴∠ABD=30°，‎ ‎∴BD=2AD=4cm，‎ 答：BD的长是4cm．-------9分 ‎22.解：（1）将点A（4，3）代入y=，得：k=12，‎ 则反比例函数解析式为y=；--------3分 九年级数学答案 第5页（共4页）‎ ‎（2）如图，过点A作AC⊥x轴于点C，‎ 则OC=4、AC=3，‎ ‎∴OA==5，---------5分 ‎∵AB∥x轴，且AB=OA=5，‎ ‎∴点B的坐标为（9，3）；-----------6分 ‎（3）∵点B坐标为（9，3），‎ ‎∴OB所在直线解析式为y=x，‎ 由可得点P坐标为（6，2），--------7分 过点P作PD⊥x轴，延长DP交AB于点E，‎ 则点E坐标为（6，3），‎ ‎∴AE=2、PE=1、PD=2，--------8分 则△OAP的面积=×（2+6）×3﹣×6×2﹣×2×1=5．-------9分 ‎22.解：（1）设年销售量y与销售单价x的函数关系式为y=kx+b（k≠0），‎ 将（40，600）、（45，550）代入y=kx+b，得：‎ ‎，解得：，--------3分 ‎∴年销售量y与销售单价x的函数关系式为y=﹣10x+1000．------4分 ‎（2）设此设备的销售单价为x万元/台，则每台设备的利润为（x﹣30）万元，销售数量为（﹣10x+1000）台，-------5分 根据题意得：（x﹣30）（﹣10x+1000）=10000，---------7分 整理，得：x2﹣130x+4000=0，‎ 解得：x1=50，x2=80．---------8分 ‎∵此设备的销售单价不得高于70万元，‎ ‎∴x=50．[来源:学.科.网]‎ 答：该设备的销售单价应是50万元/台．--------9分 ‎23.解：（1）当x=0时，y=4，即C（0，4），‎ 当y=0时，x+4=0，解得x=﹣4，即A（﹣4，0），‎ 将A、C点坐标代入函数解析式，得 ‎，‎ 解得，‎ 抛物线的表达式为y=﹣﹣x+4；---------3分 ‎（2）PQ=2AO=8，‎ 又PQ∥AO，即P、Q关于对称轴x=﹣1对称，‎ PQ=8，﹣1﹣4=﹣5，--------4分 九年级数学答案 第5页（共4页）‎ 当x=﹣5时，y=﹣×（﹣5）2﹣（﹣5）+4=﹣，即P（﹣5，﹣）；‎ ‎﹣1+4=3，即Q（3，﹣）；‎ P点坐标（﹣5，﹣），Q点坐标（3，﹣）；----------7分 ‎（3）∠MCO=∠CAB=45°，‎ ‎①当△MCO∽△CAB时， =，即=，‎ CM=．‎ 如图1，‎ 过M作MH⊥y轴于H，MH=CH=CM=，‎ 当x=﹣时，y=﹣+4=，‎ ‎∴M（﹣，）；‎ 当△OCM∽△CAB时， =，即=，解得CM=3，‎ 如图2，‎ 过M作MH⊥y轴于H，MH=CH=CM=3，‎ 当x=﹣3时，y=﹣3+4=1，‎ ‎∴M（﹣3，1），‎ 综上所述：M点的坐标为（﹣，），（﹣3，1）．--------11分 ‎　‎ 九年级数学答案 第5页（共4页）‎ 九年级数学答案 第5页（共4页）‎