- 1.85 MB
- 2021-10-27 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2021 希望数学少年俱乐部——八年级培训 80 题
1. 解方程:
1 1 1
3, 0
x b c x c a x a b
a b c a b c
2. 设 3 2x ,则 7 6 5 4 3 23 10 29 2 1x x x x x x x =_________.
3. 设 a、b、c、d 为正实数,aad.有一个三角形的三边长分别
为
2 22 2 2 2, ,a c b d b a d c ,则此三角形的面积为________.
4. 分解因式: )5()4)(3)(2)(1( xxxxxx =______________.
5. a、b、c 是正整数,并且满足等式 20041 cbabcacababc ,那
么 a+b+c 的最小值是____________.
6. a、b、c 为正整数,且 432 cba ,求 c 的最小值是_______.
7. 满足方程组
44
23
ab bc
ac bc
的正整数组(a,b,c)的个数是_________.
8. 已知方程组:
2 2
2 2
1
1
0
a b
c d
ac bd
,求 ab+cd 的值.
9. 已知关于 x 的方程 4 3 22 3 2 2 0x x k x k x k 有实根,并且所有实
根的乘积为 – 2,则所有实根的平方和为 .
10. 设一元二次方程 x2+bx+c=0 的两根为 98,99.在二次函数 y=x2+bx+c 中,
若 x 取 0,1,2,3,……,100,则 y 的值能被 6 整除的个数是_______.
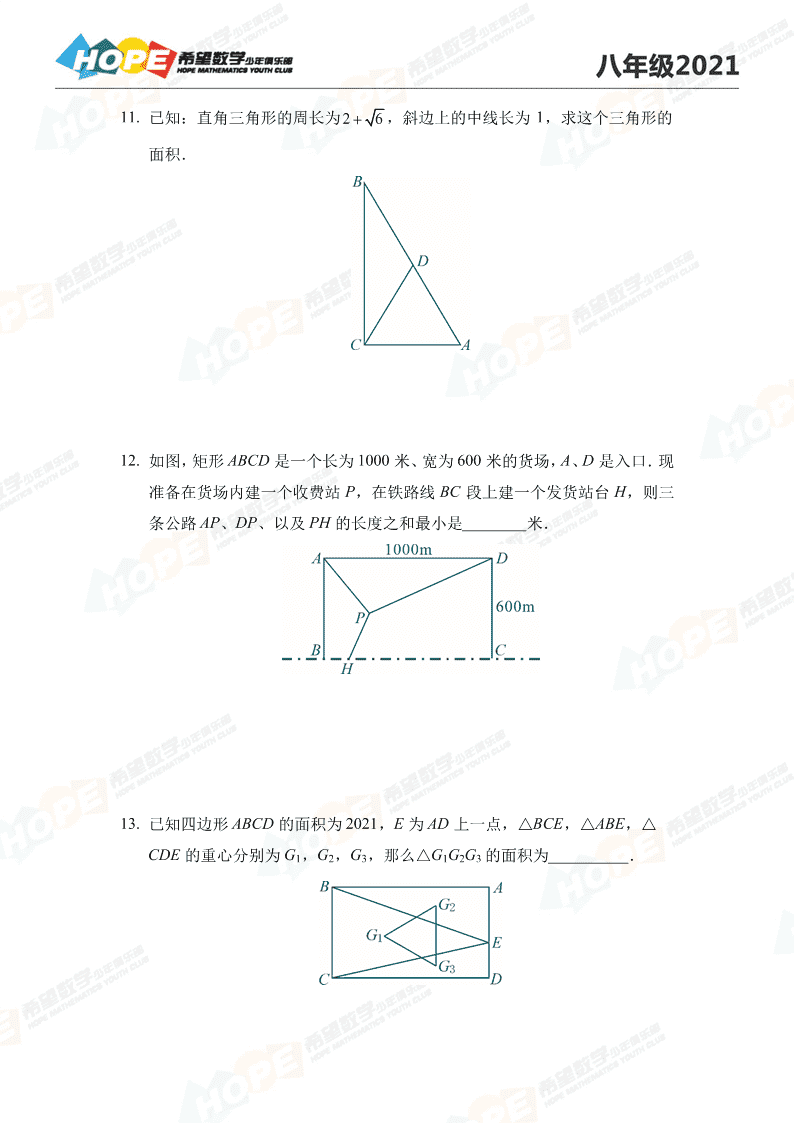
11. 已知:直角三角形的周长为 2 6 ,斜边上的中线长为 1,求这个三角形的
面积.
12. 如图,矩形 ABCD 是一个长为 1000 米、宽为 600 米的货场,A、D 是入口.现
准备在货场内建一个收费站 P,在铁路线 BC 段上建一个发货站台 H,则三
条公路 AP、DP、以及 PH 的长度之和最小是________米.
13. 已知四边形 ABCD 的面积为 2021,E 为 AD 上一点,△BCE,△ABE,△
CDE 的重心分别为 G1,G2,G3,那么△G1G2G3 的面积为__________.
14. 2009x y 的正整数解(x, y)中,x + y 的最大值为________.
15. 已知∠BAC=90°,四边形 ADEF 是正方形且边长为 1,求
1 1 1
AB BC CA
的
最大值.
16. 设 a 为 3+ 5 3 5 的小数部分,b 为 6+3 3 6 3 3 的小数部分,
则
1
b a
的值为___________.
17. 设 [x] 表示不大于 x 的最大整数,例如 [3.15]=3,[3.7]=3,[3]=3,则
3 3 3 31 2 3 2 3 4 3 4 5 2000 2001 2002
=__________.
18. 解不等式:
2
2
4
2 9
1 1 2
x
x
x
.
19. 若 3, 6, 9,
ab bc ac
a b b c a c
则
c
ab
=________.
20. 已 知 方 程 组
1
2
a x y c
a x y c
的 解 是
2
7
x
y
, 则 关 于 x , y 的 方 程 组
1 1 1
2 2 2
3
3
a x y a c
a x y a c
的解是( ).
A.
1
3
7
5
x
y
B.
1
3
5
7
x
y
C.
3
5
x
y
D.
1
3
5
7
x
y
21. 如图所示,在平行四边形 ABCD 中,点 E,F,G,H 分别是 AD, CD, AB,
BC 的中点,点 I 是线段 EF 的中点,则△GHI 与四边形 AEIG 的面积的比是
________.
22. 凸 n 边形恰有 5 个钝角,这 5 个角的和等于 780°,那么 n 的值是________.
23. 如图,在正方形 ABCD中 E 是 BC 边的中点,折叠正方形使点 A 与 E 重合,
折痕为MN ,若正方形的面积为 64,则梯形 ADMN 的面积为________.
24. 将直径 AB = 1 的半圆形纸片平放在桌面上,然后让它绕直径的一个端点旋转
到某个位置,这时它扫过的面积为 π,则 AB 旋转的角度为________°.
25. 如图所示,圆柱体饮料瓶的高是 8 厘米,上、下底面的直径是 8 厘米.上底
面开有一个小孔供插吸管用,小孔距离上底面圆心 2 厘米,那么吸管在饮料
瓶中的长度最多是________厘米.
26. 直角三角形有一条直角边为 13,另外两边的长是自然数,那么它的周长等于
________.
27. 计算机将信息转换成二进制数来处理.二进制是“逢二进一”,如二进制数
10011 转换成十进制数是 4 3 2 1 01 2 0 2 0 2 1 2 1 2 19 ,那么二进制
数 2
2021 1
(111 111)
个
转换成十进制数是( ) .
A. 20212 B. 20212 C. 20222 D. 20212
28. 如图,在△ABC 中,若
7 3 21 2 4
2
AC AC AC
AB
,则 BC 边上的
中线 AD 的取值范围是( ).
A. 2 16AD B. 0 16AD C. 1 8AD D. 3 8AD
29. 计算: 2019 2020 2021 2022 1 2021 =________.
30. 已知 2021 201 的整数部分是 m,小数部分是 n,则
2021
201
m
n
=________.
31. | 2021| | 2022 |x x 的最大值与最小值的差为________.
32. 比较大小:
4 4 4 5
1 1 1 1
+ + + +
2 2 +1 2 +2 2 1
_______1(填“>”,“<”或“=”).
33. 已知质数 p 与 q 满足 5p+7q=101,则(p+1)(q+2) = ________.
34. 某工程的施工费用不得超过 230 万元.该工程若由甲公司承担,需用 18 天,
每天付费 15 万元;若由乙公司承担,需用 27 天,每天付费 8 万元.为缩短
工期,决定由甲公司先工作 m 天,余下的工作由乙公司完成.那么 m=
________时,总工期最短.
35. 在平面直角坐标系 xOy 中,若将直线 y=3x+2 先沿 y 轴方向向上平移 9 个
单位,再沿 x 轴方向向右平移_______个单位,最后得到的直线与原直线重
合.
36. 已知△ABC 三边的长 a、b、c 满足
4 1 3
a c b
,那么∠A 是________(填“锐
角”,“直角”,“补角”).
37. 如图所示,过原点的直线与反比例函数
6
y
x
的图象交于点 A,C,过点 A,
C 分别作 x 轴的垂线,垂足为 B,D,那么四边形 ABCD 的面积为________.
38. 如图所示, 等边△ABC 位于第一象限内, B 点的坐标为(1,4), AC 平行
于 y 轴, AC=3, 若反比例函数 ( 0)
k
y
x
的图像与等边△ABC 有交点,
则 k 的最小值是________.
39. 在平面直角坐标系中,点 A 的坐标为(4,0),点 B 的坐标为(4,10),点 C 在
y 轴上,且△ABC 是直角三角形,则满足条件的 C 点有________个.
40. 如图,P 为边长为 2 的正三角形中任意一点,连接 PA、PB、P C,过 P 点分
别做三边的垂线,垂足分别为 D、E、F,则阴影部分的面积为__________.
41. 如图,若①②③④⑤五个平行四边形拼成一个含 30°内角的菱形 EFGH(不
重复、无缝隙).已知①②③④四个平行四边形面积的和为 14,四边形 ABCD
的面积为 11,则菱形 EFGH 的周长为 .
42. 如图,等腰梯形 ABCD 中,AD∥BC,∠B=45°,P 是 BC 边上一点,△PAD
的面积为
2
1
,∠APD=90°,则 AD 的最小值为 .
43. 如果一条直线 l 经过不同三点 A a b B b a C a b b a , , , , , ,那么直线 l 经
过( )
A.二、四象限 B.一、二、三象限
C.二、三、四象限 D.一、三、四象限
44. 如图,在反比例函数
2
y
x
( 0)x 的图象上,有点 1 2 3 4P P P P, , , ,它们的横坐标
依次为 1,2,3,4.分别过这些点作 x 轴与 y 轴的垂线,图中所构成的阴影
部分的面积从左到右依次为 1 2 3S S S, , ,则 1 2 3S S S ________.
45. 一个凸 n 边形的内角和小于 2021°,那么 n 的最大值是______.
46. 已知: 3 3 34 2 1a ,那么
2 3
3 3 1
a a a
=________.
47. 若实数 x,y,z 满足 4
1
y
x , 1
1
z
y ,
3
71
x
z ,则 xyz 的值为________.
48. 如图所示,在△ABC 中,AB=AC,AD=AE, 60BAD ,则 EDC ________
度.
49. 如图所示,在梯形 ABCD 中,AD∥BC (BC>AD), 90D ,BC=CD=12,
45ABE ,若 AE=10,则 CE 的长为________.
50. 一个正方形纸片,用剪刀沿一条不过任何顶点的直线将其剪成两部分;拿出
其中一部分,再沿一条不过任何顶点的直线将其剪成两部分;又从得到的三
部分中拿出其中之一,还是沿一条不过任何顶点的直线将其剪成两部分……
如此下去,最后得到了 34 个六十二边形和一些多边形纸片,则至少要剪的
刀数是______.
51. 10 个学生参加 n 个课外小组,每一个小组至多 5 个人,每两个学生至少都参
加某一个小组,任意两个课外小组,至少可以找到两个学生,他们都不在这
两个课外小组中.求 n 的最小值.
52. 方程 的整数解(x,y)的个数是( ).
(A)0 (B)1 (C)3 (D)无穷多
53. 已 知 对 于 任 意 正 整 数 n , 都 有 , 则
________.
3 2 36 5 2x x x y y
3
1 2 na a a n
2 3 100
1 1 1
1 1 1a a a
54. 如图,在四边形 ABCD 中,∠B=135°,∠C=120°,AB= 2 3 ,BC= 4 2 2 ,
CD= 4 2 ,则 AD 边的长为( ).
(A) 2 6 (B) 64 (C) 64 (D) 622
55. 如图,在平面直角坐标系 xOy 中,多边形 OABCDE 的顶点坐标分别是 O(0,
0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线 l 经过
点 M(2,3),且将多边形 OABCDE 分割成面积相等的两部分,则直线 l 的
函数表达式是________.
56. 如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形. ,
AD = 3,BD = 5,则 CD 的长为________.
57. 如图,点 D,E 分别是△ABC 的边 AC,AB 上的点,直线 BD 与 CE 交于点
F,已知△CDF,△BFE,△BCF 的面积分别为 3,4,5,则四边形 AEFD 的
面积是____________.
58. 设 a= 3 3 ,b 是 a2 的小数部分,则(b+2)3 的值为____________.
59. 如图,在 Rt△OAB 中,∠AOB=30°,AB=2,将 Rt△OAB 绕 O 点顺时针旋转
90°得到 Rt△OCD,则 AB 扫过的面积为________.
60. 已知 ABC 的最大边 BC 上的高线 AD 和中线 AM 恰好把 BAC 三等分,
3AD ,则 AM ________.
61. 已知正实数 x,y,z 满足: 1xy yz zx ,且
2 2 2 2 2 2( 1)( 1) ( 1)( 1) ( 1)( 1)
4
x y y z z x
xy yz zx
,求
1 1 1
xy yz zx
的值.
62. 不超过 615 的最大整数是( )
A.1142 B.1145 C.1148 D.1151
63. 如图,小悦测出家里的瓷砖的长为 24 厘米,宽为 10 厘米,而且还测出了边
上的中间线段均为 4 厘米,那么中间菱形的面积是多少平方厘米?
64. 如图,面积为 1 的正方形 ABCD 以 C 为旋转中心,顺时针旋转 45 度得到正
方形 CEFG,再顺时针旋转 45 度得到正方形 CHID.BD 交 CG 于 M,ME 交
DH 于 O,求四边形 FGMO 的面积.
65. 如果 a,b,c 是正数,且满足 a+b+c=9,
1 1 1 10
9a b b c c a
,那么
c a b
a b b c c a
_________.
66. P 是三角形 ABC 内一点,已知 20ABC , 30ACB , 10PBC ,
20PCB ,求 PAB 的度数.
67. 如图,ABCD 为正方形, 90BEC , 35BE , 21CE ,则阴影部分面积
为_______.
68. 计算:
)6435)(6427)(6419)(6411)(643(
)6439)(6431)(6423)(6415)(647(
44444
44444
=__________.
69. 如图,已知△ABC 中,AB = AC,P,Q 分别为 AC,AB 上的点,且 AP = PQ
= QB = BC,求∠PCQ.
70. 如图,在△ABC中,∠BAC = 120°,P是△ABC内一点,若记 ,
,则( ).
A. B. C. D. 与 y 的大小关系不确定
x PA PB PC
y AB AC
x y x y x y x
71. 如图,在△ABC 中,∠BAC =∠BCA = 44°,M 为△ABC 内一点,使∠MCA
= 30°,∠MAC = 16°,求∠BMC 度数.
72. 比 6( 6 5) 大的最小整数是多少?
73. 设实数 x,y 满足 2 2( 1)( 1) 1x x y y ,求 x+y 的值.
74. 求代数式 2 8 41 4 13x x x x 的最小值.
75. 若 3 5 2 , 3 2 5x y x y ,则 xy = _____.
76. 计算 14 6 5 14 6 5 的值为_______.
A.1 B. 5 C. 2 5 D. 5
77. a,b,c 为有理数,且等式 2 3 5 2 6a b c 成立,则 2a+999b+1001c
的值是_______.
A.1999 B. 2000 C. 2001 D. 不能确定
78. 如图,在矩形 ABCD 中,AB=20cm,BC=10cm.若在 AC,AB 上各取一点 M,
N,使 BM+MN 的值最小,那么这个最小值为多少 cm?
79. 如图,已知边长为 4 的正方形钢板,有一个角锈蚀,其中 AF = 2,BF = 1.为
了合理利用这块钢板,将在五边形 EABCD 内截取一个矩形块 MDNP,使点
P 在 AB 上,且要求面积最大,求钢板的最大利用率.
80. 如图,圆锥的母线长 OA = 6,底面圆的半径为 2.一小虫在圆锥底面的点 A
处绕圆锥侧面一周又回到点 A,则小虫所走的最短距离为_______.
A.12 B.4π C.6 2 D.6 3
2021 希望数学少年俱乐部——八年级培训 80 题答案
1. 解方程:
1 1 1
3, 0
x b c x c a x a b
a b c a b c
答案:x=a+b+c
2. 设 3 2x ,则 7 6 5 4 3 23 10 29 2 1x x x x x x x =_________.
答案: 23 3 2 10 6
3. 设 a、b、c、d 为正实数,aad.有一个三角形的三边长分别
为
2 22 2 2 2, ,a c b d b a d c ,则此三角形的面积为________.
答案:
1
2
bc ad
4. 分解因式: )5()4)(3)(2)(1( xxxxxx =______________.
答案: 2( 5 3)( 5 8)x x x x
5. a、b、c 是正整数,并且满足等式 20041 cbabcacababc ,那
么 a+b+c 的最小值是____________.
答案:171
6. a、b、c 为正整数,且 432 cba ,求 c 的最小值是_______.
答案:6
7. 满足方程组
44
23
ab bc
ac bc
的正整数组(a,b,c)的个数是_________.
答案:2
8. 已知方程组:
2 2
2 2
1
1
0
a b
c d
ac bd
,求 ab+cd 的值.
答案: 0
9. 已知关于 x 的方程 4 3 22 3 2 2 0x x k x k x k 有实根,并且所有实
根的乘积为 – 2,则所有实根的平方和为 .
答案:5
10. 设一元二次方程 x2+bx+c=0 的两根为 98,99.在二次函数 y=x2+bx+c 中,
若 x 取 0,1,2,3,……,100,则 y 的值能被 6 整除的个数是_______.
答案:67
11. 已知:直角三角形的周长为 2 6 ,斜边上的中线长为 1,求这个三角形的
面积.
答案:0.5
12. 如图,矩形 ABCD 是一个长为 1000 米、宽为 600 米的货场,A、D 是入口.现
准备在货场内建一个收费站 P,在铁路线 BC 段上建一个发货站台 H,则三
条公路 AP、DP、以及 PH 的长度之和最小是________米.
答案:500 3 600
13. 已知四边形 ABCD 的面积为 2021,E 为 AD 上一点,△BCE,△ABE,△
CDE 的重心分别为 G1,G2,G3,那么△G1G2G3 的面积为__________.
答案:
2021
9
14. 2009x y 的正整数解(x, y)中,x + y 的最大值为________.
答案:1517
15. 已知∠BAC=90°,四边形 ADEF 是正方形且边长为 1,求
1 1 1
AB BC CA
的
最大值.
答案:
2
1
4
16. 设 a 为 3+ 5 3 5 的小数部分,b 为 6+3 3 6 3 3 的小数部分,
则
2 1
b a
的值为___________.
答案: 6 2 1
17. 设 [x] 表示不大于 x 的最大整数,例如 [3.15]=3,[3.7]=3,[3]=3,则
3 3 3 31 2 3 2 3 4 3 4 5 2000 2001 2002
=__________.
答案:2001000
18. 解不等式:
2
2
4
2 9
1 1 2
x
x
x
.
答案:
1 45
0, 0
2 8
x x
19. 若 3, 6, 9,
ab bc ac
a b b c a c
则
c
ab
=________.
答案:
35
36
20. 已 知 方 程 组
1
2
a x y c
a x y c
的 解 是
2
7
x
y
, 则 关 于 x , y 的 方 程 组
1 1 1
2 2 2
5
3
a x y a c
a x y a c
的解是( ).
A.
1
3
7
5
x
y
B.
1
3
5
7
x
y
C.
3
5
x
y
D.
1
3
5
7
x
y
答案:A
21. 如图所示,在平行四边形 ABCD 中,点 E,F,G,H 分别是 AD, CD, AB,
BC 的中点,点 I 是线段 EF 的中点,则△GHI 与四边形 AEIG 的面积的比是
________.
答案:1:1
22. 凸 n 边形恰有 5 个钝角,这 5 个角的和等于 780°,那么 n 的值是________.
答案:7
23. 如图,在正方形 ABCD中 E 是 BC 边的中点,折叠正方形使点 A 与 E 重合,
折痕为MN ,若正方形的面积为 64,则梯形 ADMN 的面积为________.
答案:24
24. 将直径 AB = 1 的半圆形纸片平放在桌面上,然后让它绕直径的一个端点旋转
到某个位置,这时它扫过的面积为 π,则 AB 旋转的角度为________°.
答案:315
25. 如图所示,圆柱体饮料瓶的高是 8 厘米,上、下底面的直径是 8 厘米.上底
面开有一个小孔供插吸管用,小孔距离上底面圆心 2 厘米,那么吸管在饮料
瓶中的长度最多是________厘米.
答案:10
26. 直角三角形有一条直角边为 13,另外两边的长是自然数,那么它的周长等于
________.
答案:182
27. 计算机将信息转换成二进制数来处理.二进制是“逢二进一”,如二进制数
10011 转换成十进制数是 4 3 2 1 01 2 0 2 0 2 1 2 1 2 19 ,那么二进制
数 2
2021 1
(111 111)
个
转换成十进制数是( ) .
A. 20212 B. 20212 C. 20222 D. 20212
答案:D
28. 如图,在△ABC 中,若
7 3 21 2 4
2
AC AC AC
AB
,则 BC 边上的
中线 AD 的取值范围是( ).
A. 2 16AD B. 0 16AD C. 1 8AD D. 3 8AD
答案:C
29. 计算: 2019 2020 2021 2022 1 2021 =________.
答案:4080398
30. 已知 2021 201 的整数部分是 m,小数部分是 n,则
2021
201
m
n
=________.
答案:–1
31. | 2021| | 2022 |x x 的最大值与最小值的差为________.
答案:8086
32. 比较大小:
4 4 4 5
1 1 1 1
+ + + +
2 2 +1 2 +2 2 1
_______1(填“>”,“<”或“=”).
答案:<
33. 已知质数 p 与 q 满足 5p+7q=101,则(p+1)(q+2) = ________.
答案:45
34. 某工程的施工费用不得超过 230 万元.该工程若由甲公司承担,需用 18 天,
每天付费 15 万元;若由乙公司承担,需用 27 天,每天付费 8 万元.为缩短
工期,决定由甲公司先工作 m 天,余下的工作由乙公司完成.那么 m=
________时,总工期最短.
答案:4
35. 在平面直角坐标系 xOy 中,若将直线 y=3x+2 先沿 y 轴方向向上平移 9 个
单位,再沿 x 轴方向向右平移_______个单位,最后得到的直线与原直线重
合.
答案:3
36. 已知△ABC 三边的长 a、b、c 满足
4 1 3
a c b
,那么∠A 是________(填“锐
角”,“直角”,“补角”).
答案:锐角
37. 如图所示,过原点的直线与反比例函数
6
y
x
的图象交于点 A,C,过点 A,
C 分别作 x 轴的垂线,垂足为 B,D,那么四边形 ABCD 的面积为________.
答案:12
38. 如图所示, 等边△ABC 位于第一象限内, B 点的坐标为(1,4), AC 平行
于 y 轴, AC=3, 若反比例函数 ( 0)
k
y
x
的图像与等边△ABC 有交点,
则 k 的最小值是________.
答案:4
39. 在平面直角坐标系中,点 A 的坐标为(4,0),点 B 的坐标为(4,10),点 C 在
y 轴上,且△ABC 是直角三角形,则满足条件的 C 点有________个.
答案:4
40. 如图,P 为边长为 2 的正三角形中任意一点,连接 PA、PB、P C,过 P 点分
别做三边的垂线,垂足分别为 D、E、F,则阴影部分的面积为__________.
答案:
3
2
41. 如图,若①②③④⑤五个平行四边形拼成一个含 30°内角的菱形 EFGH(不
重复、无缝隙).已知①②③④四个平行四边形面积的和为 14,四边形 ABCD
的面积为 11,则菱形 EFGH 的周长为 .
答案:24
42. 如图,等腰梯形 ABCD 中,AD∥BC,∠B=45°,P 是 BC 边上一点,△PAD
的面积为
2
1
,∠APD=90°,则 AD 的最小值为 .
答案: 2
43. 如果一条直线 l 经过不同三点 A a b B b a C a b b a , , , , , ,那么直线 l 经
过( )
A.二、四象限 B.一、二、三象限
C.二、三、四象限 D.一、三、四象限
答案:A
44. 如图,在反比例函数
2
y
x
( 0)x 的图象上,有点 1 2 3 4P P P P, , , ,它们的横坐标
依次为 1,2,3,4.分别过这些点作 x 轴与 y 轴的垂线,图中所构成的阴影
部分的面积从左到右依次为 1 2 3S S S, , ,则 1 2 3S S S ________.
答案:1.5
45. 一个凸 n 边形的内角和小于 2021°,那么 n 的最大值是______.
答案:13
46. 已知: 3 3 34 2 1a ,那么
2 3
3 3 1
a a a
=________.
答案:1
47. 若实数 x,y,z 满足 4
1
y
x , 1
1
z
y ,
3
71
x
z ,则 xyz 的值为________.
答案:1
48. 如图所示,在△ABC 中,AB=AC,AD=AE, 60BAD ,则 EDC ________
度.
答案:30
49. 如图所示,在梯形 ABCD 中,AD∥BC (BC>AD), 90D ,BC=CD=12,
45ABE ,若 AE=10,则 CE 的长为________.
答案:4 或 6
50. 一个正方形纸片,用剪刀沿一条不过任何顶点的直线将其剪成两部分;拿出
其中一部分,再沿一条不过任何顶点的直线将其剪成两部分;又从得到的三
部分中拿出其中之一,还是沿一条不过任何顶点的直线将其剪成两部分……
如此下去,最后得到了 34 个六十二边形和一些多边形纸片,则至少要剪的
刀数是______.
答案:2005
51. 10 个学生参加 n 个课外小组,每一个小组至多 5 个人,每两个学生至少都参
加某一个小组,任意两个课外小组,至少可以找到两个学生,他们都不在这
两个课外小组中.求 n 的最小值.
答案:6
52. 方程 的整数解(x,y)的个数是( ).
(A)0 (B)1 (C)3 (D)无穷多
答案:A
53. 已 知 对 于 任 意 正 整 数 n , 都 有 , 则
________.
答案:
54. 如图,在四边形 ABCD 中,∠B=135°,∠C=120°,AB= 2 3 ,BC= 4 2 2 ,
CD= 4 2 ,则 AD 边的长为( ).
(A) 2 6 (B) 64 (C) 64 (D) 622
答案:D
55. 如图,在平面直角坐标系 xOy 中,多边形 OABCDE 的顶点坐标分别是 O(0,
0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线 l 经过
点 M(2,3),且将多边形 OABCDE 分割成面积相等的两部分,则直线 l 的
函数表达式是________.
答案:
1 11
3
y x +
3 2 36 5 2x x x y y
3
1 2 na a a n
2 3 100
1 1 1
1 1 1a a a
33
100
56. 如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形. ,
AD = 3,BD = 5,则 CD 的长为________.
答案:4
57. 如图,点 D,E 分别是△ABC 的边 AC,AB 上的点,直线 BD 与 CE 交于点
F,已知△CDF,△BFE,△BCF 的面积分别为 3,4,5,则四边形 AEFD 的
面积是____________.
答案:
204
13
58. 设 a= 3 3 ,b 是 a2 的小数部分,则(b+2)3 的值为____________.
答案:9
59. 如图,在 Rt△OAB 中,∠AOB=30°,AB=2,将 Rt△OAB 绕 O 点顺时针旋转
90°得到 Rt△OCD,则 AB 扫过的面积为________.
答案:π
60. 已知 ABC 的最大边 BC 上的高线 AD 和中线 AM 恰好把 BAC 三等分,
3AD ,则 AM ________.
答案:2
61. 已知正实数 x,y,z 满足: 1xy yz zx ,且
2 2 2 2 2 2( 1)( 1) ( 1)( 1) ( 1)( 1)
4
x y y z z x
xy yz zx
,求
1 1 1
xy yz zx
的值.
答案:1
62. 不超过 615 的最大整数是( )
A.1142 B.1145 C.1148 D.1151
答案:C
63. 如图,小悦测出家里的瓷砖的长为 24 厘米,宽为 10 厘米,而且还测出了边
上的中间线段均为 4 厘米,那么中间菱形的面积是多少平方厘米?
答案:64
64. 如图,面积为 1 的正方形 ABCD 以 C 为旋转中心,顺时针旋转 45 度得到正
方形 CEFG,再顺时针旋转 45 度得到正方形 CHID.BD 交 CG 于 M,ME 交
DH 于 O,求四边形 FGMO 的面积.
答案:0.5
65. 如果 a,b,c 是正数,且满足 a+b+c=9,
1 1 1 10
9a b b c c a
,那么
c a b
a b b c c a
_________.
答案:7
66. P 是三角形 ABC 内一点,已知 20ABC , 30ACB , 10PBC ,
20PCB ,求 PAB 的度数.
答案:100°
67. 如图,ABCD 为正方形, 90BEC , 35BE , 21CE ,则阴影部分面积
为_______.
答案:300
68. 计算:
)6435)(6427)(6419)(6411)(643(
)6439)(6431)(6423)(6415)(647(
44444
44444
=__________.
答案:337
69. 如图,已知△ABC 中,AB = AC,P,Q 分别为 AC,AB 上的点,且 AP = PQ
= QB = BC,求∠PCQ.
答案:30°
70. 如图,在△ABC中,∠BAC = 120°,P是△ABC内一点,若记 ,
,则( ).
A. B. C. D. 与 y 的大小关系不确定
答案:C
71. 如图,在△ABC 中,∠BAC =∠BCA = 44°,M 为△ABC 内一点,使∠MCA
= 30°,∠MAC = 16°,求∠BMC 度数.
答案:150°
x PA PB PC
y AB AC
x y x y x y x
72. 比 6( 6 5) 大的最小整数是多少?
答案:10582
73. 设实数 x,y 满足 2 2( 1)( 1) 1x x y y ,求 x+y 的值.
答案:0
74. 求代数式 2 8 41 4 13x x x x 的最小值.
答案: 2 17
75. 若 3 5 2 , 3 2 5x y x y ,则 xy = _____.
答案: 5 2
76. 计算 14 6 5 14 6 5 的值为_______.
A.1 B. 5 C. 2 D. 5
答案:C
77. a,b,c 为有理数,且等式 2 3 5 2 6a b c 成立,则 2a+999b+1001c
的值是_______.
A.1999 B. 2000 C. 2001 D. 不能确定
答案:B
78. 如图,在矩形 ABCD 中,AB=20cm,BC=10cm.若在 AC,AB 上各取一点 M,
N,使 BM+MN 的值最小,那么这个最小值为多少 cm?
答案:16
79. 如图,已知边长为 4 的正方形钢板,有一个角锈蚀,其中 AF = 2,BF = 1.为
了合理利用这块钢板,将在五边形 EABCD 内截取一个矩形块 MDNP,使点
P 在 AB 上,且要求面积最大,求钢板的最大利用率.
答案:80%
80. 如图,圆锥的母线长 OA = 6,底面圆的半径为 2.一小虫在圆锥底面的点 A
处绕圆锥侧面一周又回到点 A,则小虫所走的最短距离为_______.
A.12 B.4π C.6 2 D.6 3
答案:D