江苏省南京市秦淮区2019-2020学年度第二学期八年级 期末试题 11页

‎2019/2020学年度第二学期第二阶段学业质量监测试卷 八年级数学 注意事项：‎ ‎1．本试卷共6页．全卷满分100分．考试时间为100分钟．‎ 一、选择题（本大题共6小题，每小题2分，共12分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卷相应位置上）‎ ‎1．下列交通标志中，是中心对称图形的是 ‎ ‎ ‎ A． B． C． D．‎ ‎2．下列调查中，不适合用普查的是 A．了解全班同学每周体育锻炼的时长 ‎ B．“新冠”肺炎疫情期间检测地铁乘客的体温 C．某学校招艺术特长生，对报名学生进行面试 ‎ D．了解全国中学生每天写作业的时长 ‎3．下列运算中，正确的是 A．＋＝ B．－＝1‎ C．×＝ D．÷＝ ‎4．下列事件中，是必然事件的是 A．购买一张彩票，中奖 ‎ B．打开电视，正在播放广告 C．抛掷一枚质地均匀且6个面上分别标上数字1~6的骰子，朝上一面的数字小于7 ‎ D．一个不透明的袋子中只装有2个黑球，搅匀后从中随机摸出一个球，结果是红球 ‎5．下列分式变形中，正确的是 A．＝ B．＝ C．＝ D．＝ 八年级数学 第11页 （共6页）‎ 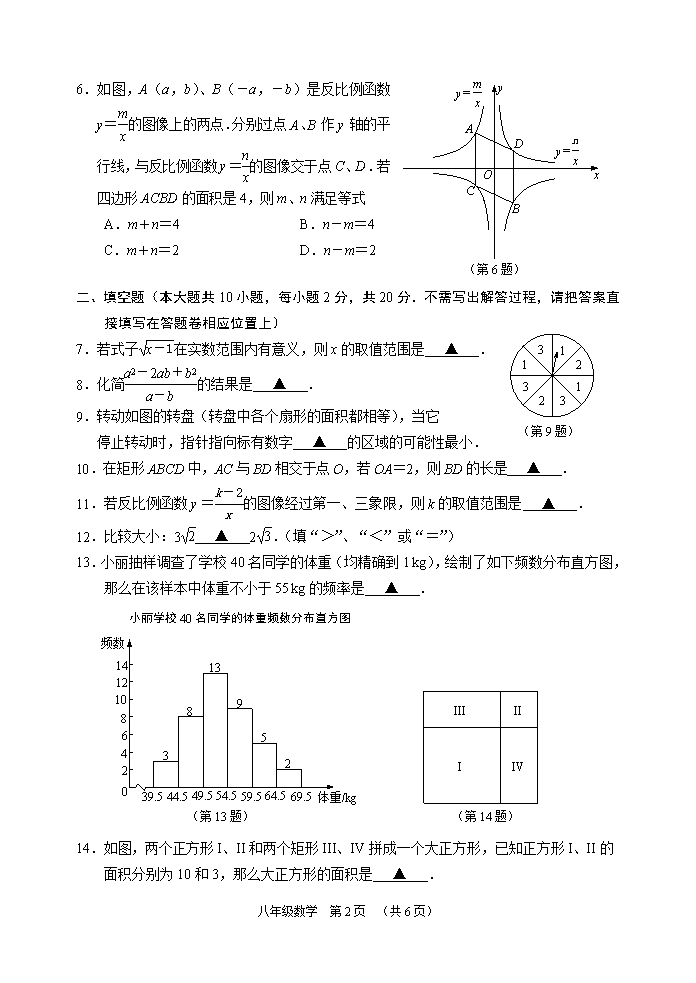y＝ y＝ ‎（第6题）‎ x y O A C B D ‎6．如图，A（a，b）、B（－a，－b）是反比例函数 y＝的图像上的两点．分别过点A、B作y轴的平行线，与反比例函数y＝的图像交于点C、D．若四边形ACBD的面积是4，则m、n满足等式 A．m＋n＝4 B．n－m＝4 ‎ C．m＋n＝2 D．n－m＝2‎ ‎（第9题）‎ ‎1‎ ‎1‎ ‎3‎ ‎2‎ ‎2‎ ‎3‎ ‎3‎ ‎1‎ 二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请把答案直接填写在答题卷相应位置上）‎ ‎7．若式子在实数范围内有意义，则x的取值范围是 ▲ ．‎ ‎8．化简的结果是 ▲ ．‎ ‎9．转动如图的转盘（转盘中各个扇形的面积都相等），当它 停止转动时，指针指向标有数字 ▲ 的区域的可能性最小．‎ ‎10．在矩形ABCD中，AC与BD相交于点O，若OA＝2，则BD的长是 ▲ ．‎ ‎11．若反比例函数y的图像经过第一、三象限，则k的取值范围是 ▲ ．‎ ‎12．比较大小：3 ▲ 2．（填“＞”、“＜”或“＝”）‎ ‎13．小丽抽样调查了学校40名同学的体重（均精确到1 kg），绘制了如下频数分布直方图，那么在该样本中体重不小于55 kg的频率是 ▲ ． ‎ ‎（第14题）‎ I II III IV 小丽学校40名同学的体重频数分布直方图 ‎3‎ ‎8‎ ‎13‎ ‎9‎ ‎2‎ ‎0‎ ‎2‎ ‎4‎ ‎6‎ ‎8‎ ‎10‎ ‎12‎ ‎14‎ ‎39.5‎ ‎69.5‎ 体重/kg 频数 ‎44.5‎ ‎49.5‎ ‎54.5‎ ‎59.5‎ ‎64.5‎ ‎（第13题）‎ ‎5‎ ‎14．如图，两个正方形I、II和两个矩形III、IV拼成一个大正方形，已知正方形I、II的 ‎ 面积分别为10和3，那么大正方形的面积是 ▲ ．‎ 八年级数学 第11页 （共6页）‎ ‎15．如图，已知∠AOB＝45°，将射线OA绕点O逆时针旋转α°（0＜α＜360），得到射线OA′．若OA′⊥OB，则α的值是 ▲ ． ‎ A B C P ‎（第16题）‎ ‎（第15题）‎ A B O ‎16．如图，在△ABC中，∠BAC＝90°，AB＝AC，P是△ABC内一点．若PA＝1，PC＝2，∠APC＝135°，则PB的长为 ▲ ．‎ 三、解答题（本大题共10小题，共68分．请在答题卷指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）‎ ‎17．（8分）解方程：（1）＝； （2）＋＝0．‎ ‎18．（8分）计算：（1）·（a≥0）； （2）×．‎ ‎19．（6分）先化简，再求值：÷，其中x＝－1．‎ ‎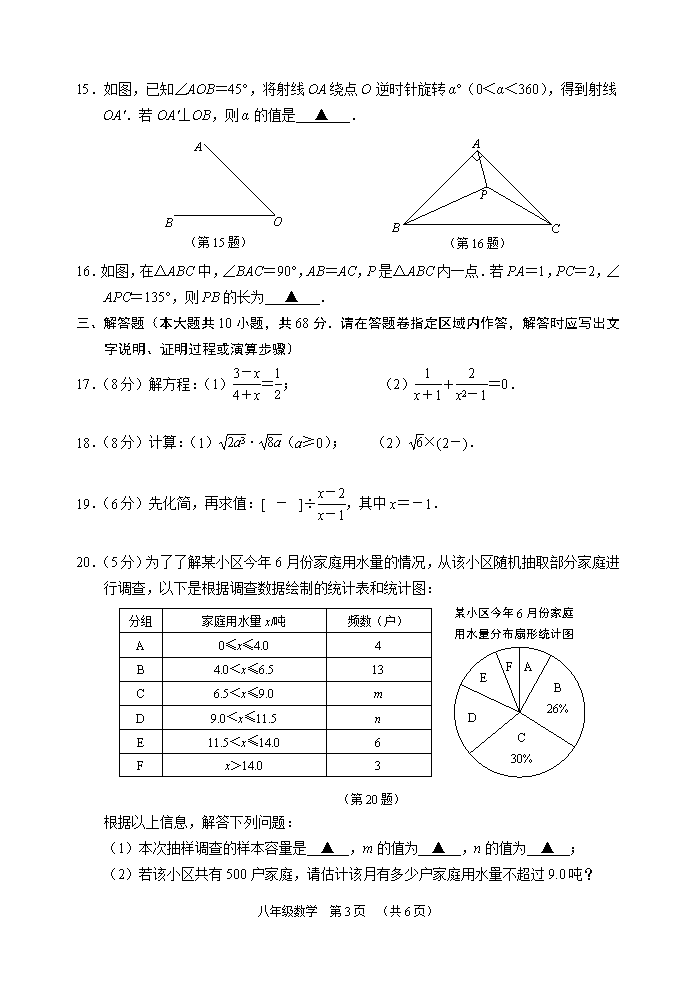20．（5分）为了了解某小区今年6月份家庭用水量的情况，从该小区随机抽取部分家庭进行调查，以下是根据调查数据绘制的统计表和统计图：‎ 分组 家庭用水量x/吨 频数（户）‎ A ‎0≤x≤4.0‎ ‎4‎ B ‎4.0＜x≤6.5‎ ‎13‎ C ‎6.5＜x≤9.0‎ m D ‎9.0＜x≤11.5‎ n E ‎11.5＜x≤14.0‎ ‎6‎ F x＞14.0‎ ‎3‎ ‎（第20题）‎ A B ‎26%‎ C ‎30%‎ D E F 某小区今年6月份家庭 用水量分布扇形统计图 根据以上信息，解答下列问题：‎ ‎（1）本次抽样调查的样本容量是　▲　，m的值为　▲　，n的值为　▲　；‎ ‎（2）若该小区共有500户家庭，请估计该月有多少户家庭用水量不超过9.0吨？‎ 八年级数学 第11页 （共6页）‎ ‎21．（6分）在压力不变的情况下，某物体所受到的压强p（Pa）与它的受力面积S（m2）之间成反比例函数关系，其图像如图所示．‎ ‎（1）求p与S之间的函数表达式；‎ ‎（第21题）‎ ‎2000‎ ‎1000‎ ‎4000‎ ‎0.1‎ ‎0.2‎ ‎0.3‎ ‎0.4‎ ‎0.5‎ S/m2‎ p/Pa ‎3000‎ O ‎（2）当S＝0.4 m2时，求该物体所受到的压强p．‎ A B C D E F ‎（第22题）‎ G H ‎22．（6分）如图，四边形ABCD是菱形，E、F、G、H分别是边AB、BC、CD、DA的中点，连接EF、FG、GH、HE．‎ 求证：四边形EFGH是矩形．‎ ‎23．（6分）甲、乙两公司为“见义勇为基金会”各捐款30 000元．已知乙公司比甲公司人均多捐20元，且甲公司的人数比乙公司的人数多20%．‎ ‎ 设乙公司有x人． ‎ ‎（1）用含x的代数式填表（结果不需要化简）：‎ 人均捐款额（元/人）‎ 人数 捐款总额（元）‎ 甲公司 ‎ ▲ ·‎ ‎ ▲ ·‎ ‎30 000‎ 乙公司 ‎ ▲ ·‎ ‎ x·‎ ‎30 000‎ ‎（2）求x的值．‎ ‎ ‎ 八年级数学 第11页 （共6页）‎ 如图，已知线段AB、BC．用直尺和圆规作□ABCD．‎ ‎（保留作图痕迹，不写作法）‎ A ‎ ‎ B ‎ ‎ C ‎24．（6分）题目：‎ ‎ ‎ ‎（小明作的图）‎ A B C D ‎（1）下图是小明所作的图，根据作图痕迹，可以知道他作图的依据是“ ▲ 的四边形是平行四边形”；‎ ‎（2）请你以“对角线互相平分的四边形是平行四边形”为依据完成题目中的作图．‎ ‎ ‎ ‎25．（8分）‎ ‎ （1）分式有意义的条件是 ▲ ，该分式的值 ▲ （填“会”或“不会”）为零，由此可以判断出反比例函数y＝的图像与y轴和x轴都没有公共点．‎ ‎（2）类比（1），下列直线中，与函数y＝－2的图像没有公共点的是 ▲ ．（填写所有满足要求的选项的序号）‎ ‎①经过点（1，0）且平行于y轴的直线；‎ ‎②经过点（－1，0）且平行于y轴的直线；‎ ‎③经过点（0，2）且平行于x轴的直线；‎ ‎④经过点（0，－2）且平行于x轴的直线．‎ ‎ （3）已知函数y＝－2的图像可以由y＝的图像平移得到．请你结合（2）中的结论，画出函数y＝－2的图像，并写出该函数的两条不同类型的性质．‎ 八年级数学 第11页 （共6页）‎ ‎26．（9分）我们知道，平行四边形的对边平行且相等．利用这一性质，可以为证明线段之间的位置关系和数量关系提供帮助．‎ ‎ 重温定理，识别图形 ‎ （1）如图①，我们在探究三角形中位线DE和第三边BC的关系时，所作的辅助线为“延长DE到点F，使EF＝DE，连接CF”，此时DE与DF在同一直线上且DE＝DF，又可证图中的四边形 ▲ 为平行四边形，可得BC与DF的关系是 ▲ ，于是推导出了“DE∥BC，DE＝BC”．‎ ‎①‎ A C B D E F ‎②‎ A B C D E F G H ‎ 寻找图形，完成证明 ‎（2）如图②，四边形ABCD和四边形AEFG都是正方形，△BEH是等腰直角三角形，‎ ‎∠EBH＝90°，连接CF、CH．求证CF＝BE．‎ ‎③‎ A B C D E F G ‎ 构造图形，解决问题 ‎（3）如图③，四边形ABCD和四边形AEFG 都是菱形，∠ABC＝∠AEF＝120°，‎ 连接BE、CF．‎ 直接写出CF与BE的数量关系．‎ 八年级数学 第11页 （共6页）‎ ‎2019-2020学年度第二学期第二阶段学业质量监测 八年级数学参考答案及评分标准 说明：本评分标准每题给出了一种或几种解法供参考，如果考生的解法与本解答不同，参照本评分标准的精神给分．‎ 一、选择题（每小题2分，共计12分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 答案 A D C C B D 二、填空题（每小题2分，共计20分）‎ ‎7．x≥1 8．a－b 9．2 10．4 11．k＞2‎ ‎12．＞ 13．0.4 14．13＋2 15．135或315 16． 三、解答题（本大题共10小题，共计68分）‎ ‎17．（本题8分）‎ 解：（1）方程两边同乘2(4＋x)，得2(3－x)＝4＋x． 2分 解这个方程，得x＝． 3分 检验：当x＝时，2(4＋x)＝≠0，x＝是原方程的解． 4分 ‎（2）方程两边同乘(x＋1)(x－1)，得x－1＋2＝0． 6分 解这个方程，得x＝－1． 7分 检验：当x＝－1时，(x＋1)(x－1)＝0，x＝－1是增根，原方程无解． 8分 ‎18．（本题8分）‎ 解：（1）原式＝ 1分 ‎ ‎＝ 2分 ‎＝4a2． 4分 ‎（2）原式＝×2－× 5分 ‎＝12－ 7分 ‎＝11． 8分 ‎19．（本题6分）‎ 解：方法一 原式＝· 2分 ‎＝· 3分 ‎＝· 4分 八年级数学 第11页 （共6页）‎ ‎＝． 5分 当x＝－1时，原式＝＝－． 6分 方法二 原式＝·－· 1分 ‎ ‎＝－ 3分 ‎＝ 4分 ‎＝． 5分 当x＝－1时，原式＝＝－． 6分 ‎20．（本题5分）‎ 解：（1）50，15，9． 3分 ‎ （2）(4＋13＋15)÷50＝0.64，‎ ‎500×0.64＝320（户）．‎ ‎ 答：估计该月用水量不超过9.0吨的家庭数为320户． 5分 ‎ （说明：不写答，但答案中有单位，不扣分．）‎ ‎21．（本题6分）‎ 解：（1）设p与S之间的函数表达式为p＝． 1分 图像经过点（0.1，1000），‎ 把S＝0.1，p＝1000代入p＝，得1000＝． 2分 解得k＝100． 3分 所以p与S之间的函数表达式为p＝． 4分 ‎（2）当S＝0.4 m2时，p＝＝250（Pa）． 5分 答：当S＝0.4 m2时，该物体所受到的压强p为250 Pa． 6分 A B C D E F ‎（第22题）‎ G H O P ‎22．（本题6分）‎ 证明：连接AC、BD，AC与BD相交于点O，AC与EH相交于点P．‎ 八年级数学 第11页 （共6页）‎ ‎∵E、F分别是边AB、BC的中点，‎ ‎∴EF∥AC，EF＝AC． 1分 同理GH∥AC，GH＝AC． 2分 ‎∴EF∥GH，EF＝GH．∴四边形EFGH是平行四边形． 3分 ‎∵四边形ABCD是菱形，∴AC⊥BD，即∠AOB＝90°． 4分 ‎∵E、H分别是边AB、AD的中点，∴EH∥BD．‎ ‎∴∠APE＝∠AOB＝90°．‎ ‎∵EF∥AC，∴∠FEH＝∠APE＝90°． 5分 ‎∴四边形EFGH是矩形． 6分 ‎23．（本题6分）‎ 解：（1）答案不唯一，如分别填，(1＋20%)x，． 3分 ‎（2）本题方程不唯一，如根据（1）填的代数式，可得－＝20． 4分 ‎ 解这个方程，得x＝250． 5分 ‎ 经检验，x＝250是原方程的解． 6分 ‎24．（本题6分）‎ A B C D ‎（第24题）‎ 解：（1）一组对边平行且相等． 2分 ‎（2）‎ ‎ ‎ ‎ 如图，□ABCD即为所求． 6分 ‎ （说明：不写结论，扣1分．）‎ ‎25．（本题8分）‎ 解：（1）x≠0；不会． 2分 八年级数学 第11页 （共6页）‎ ‎（2）①④． 4分 ‎（3）列表：‎ x ‎…‎ ‎－2‎ ‎－1‎ ‎0‎ ‎1 ‎1 ‎2‎ ‎3‎ ‎4‎ ‎…‎ y＝－2‎ ‎…‎ ‎－2 ‎－2 ‎－3‎ ‎－4‎ ‎－5‎ ‎1‎ ‎0‎ ‎－1‎ ‎－1 ‎－1 ‎…‎ ‎（第25题）‎ x y O ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎5‎ ‎4‎ ‎3‎ ‎2‎ ‎1‎ ‎-1‎ ‎-2‎ ‎-3‎ ‎-4‎ ‎-5‎ ‎-5‎ ‎-4‎ ‎-3‎ ‎-2‎ ‎-1‎ ‎ 描点、连线．‎ ‎ 如图所示：‎ ‎ 图像正确． 6分 ‎ （说明：图像正确，但没有列表，不扣分．）‎ ‎ 函数的性质有：①当x＜1或x＞1时，y随x的增大而减小； 7分 ‎ ②该图像关于点（1，－2）对称． 8分 ‎26．（本题9分）‎ 解：（1）DBCF；BC∥DF，BC＝DF． 2分 ‎ （2）在正方形ABCD和等腰直角三角形BEH中，‎ ‎∠ABC＝∠EBH＝90°，BA＝BC，BE＝BH．‎ ‎∴∠ABE＝∠CBH．‎ ‎∴△ABE≌△CBH．‎ ‎②‎ A B C D E F G H ‎∴AE＝CH，∠AEB＝∠CHB． 3分 在正方形AEFG中，AE＝EF，∠AEF＝90°．‎ ‎∴EF＝CH．‎ 在等腰直角三角形BEH中，∠BEH＝∠BHE＝45°．‎ ‎∴∠AEB＋∠FEH＝360°－∠BEH－∠AEF＝225°．‎ 八年级数学 第11页 （共6页）‎ ‎∴∠CHB＋∠FEH＝225°．‎ ‎∵∠BHE＝45°，‎ ‎∴∠CHE＋∠FEH＝225°－45°＝180°．‎ ‎∴EF∥CH． 4分 ‎∴四边形EHCF是平行四边形． 5分 ‎∴CF＝EH． 6分 ‎∵EH＝＝＝BE，∴CF＝BE． 7分 ‎（3）CF＝BE． 9分 ‎（方法如下：‎ 作等腰△BEH，使BH＝BE，∠EBH＝120°，连接CH．‎ 在菱形ABCD和等腰三角形BEH中，‎ ‎（第26题）‎ ‎③‎ A B C D E F G H ‎∵∠ABC＝∠EBH＝120°，∴∠ABE＝∠CBH．‎ ‎∵BA＝BC，BE＝BH，∴△ABE≌△CBH． ‎ ‎∴AE＝CH，∠AEB＝∠CHB．‎ 在菱形AEFG中，∵AE＝EF，∴EF＝CH．‎ ‎∵∠BEH＝(180°－∠EBH)÷2＝30°，∠AEF＝120°，‎ ‎∴∠AEB＋∠FEH＝360°－∠BEH－∠AEF＝210°．‎ ‎∴∠CHB＋∠FEH＝210°．‎ ‎∵∠BHE＝(180°－∠EBH)÷2＝30°，‎ ‎∴∠CHE＋∠FEH＝210°－30°＝180°．∴EF∥CH．‎ ‎∴四边形EHCF是平行四边形．∴CF＝EH．‎ 在△BEH中，易证EH＝BE．∴CF＝BE．）‎ 八年级数学 第11页 （共6页）‎