华师版数学八年级下册同步课件-第17章 函数及其图象-17 24页

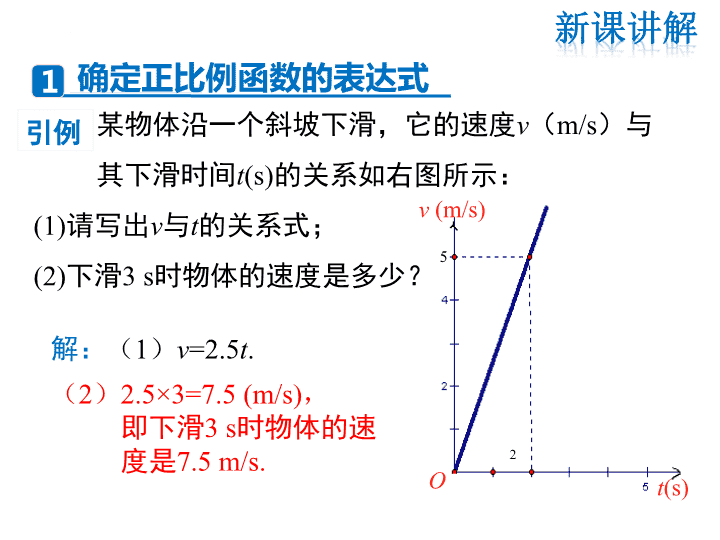
第17章 函数及其图象 17.3 一次函数 4 求一次函数的表达式 　　前面，我们学习了一次函数及其图象和性质， 你能写出两个具体的一次函数表达式吗？如何画出 它们的图象？ 2 3y x=- +3 1y x= - 两点法——两点确定一条直线 反过来，已知一个一次函数图象经过的两个具 体的点，你能求出它的表达式吗？ 思考 某物体沿一个斜坡下滑，它的速度v（m/s）与 其下滑时间t(s)的关系如右图所示： (1)请写出v与t的关系式； (2)下滑3 s时物体的速度是多少？ v (m/s) t(s)O 解：（1）v=2.5t. （2）2.5×3=7.5 (m/s)， 即下滑3 s时物体的速 度是7.5 m/s. 5 2 确定正比例函数的表达式1 引例 　　 求正比例函数 的表达式． 解：由正比例函数的定义，得 m2－15＝1且m－4≠0， ∴m＝－4， ∴y＝－8x. 解题技巧：利用正比例函数的定义确定表达式： 自变量的指数为1，系数不为0. 152 )4(  mxmy例1 确定正比例函数的表达式需要几个条件？ 确定一次函数的表达式呢？ 一个 两个 想一想 如图，已知一次函数的图象经过P（0，-1）、 Q（1，1）两点，怎样确定这个一次函数的表达式呢？ 确定一次函数的表达式2 一次函数的一般形式是y=kx+b（k、b为常数， k≠0），要求出一次函数的表达式，关键是要确 定k和b的值（即待定系数）. 函数表达式 y=kx+b 满足条件的两点 (x1，y1)，(x2，y2) 一次函数的图象 直线l 选取 解出 画出 选取 因为P（0，-1） 和Q（1，1）都在该函数图象上， 因此它们的坐标应满足y=kx+b ， 将这两点坐标代入 该式，得到一个关于k、b的二元一次方程组： 解这个方程组，得 所以，这个一次函数的表达式为 y = 2x- 1. 0 1 1 . k b k b        ， 2 1. k b     ， 温度计是利用水银或酒精热胀冷缩的工作原理 制作的，温度计中水银柱的高度y是温度x的一次函数. 某种型号的实验用水银温度计能测量-20 ℃至100 ℃ 的温度.已知10 ℃ 时水银柱高10厘米，50 ℃时水银 柱高18厘米，求这个函数的表达式. 解：设所求的函数表达式为y=kx+b(k≠0).根据题意，得 10k+b=10， k=0.2， 50k+b=18， b=8. 所以，所求的函数表达式是y=0.2x+8.  解得 例2 如果知道一个一次函数，当自变量 x=4时，函数值y=5；当x=5时，y=2.你能 画出它的图象，并写出函数表达式吗？ 4  解：设函数表达式为y=kx+b. 由题意，得 解得 4k+b=5， 5k+b=2， 所以，函数表达式为 y=-3x+17，图象如图所示. k=-3， b=17.5  2  5  例3 利用二元一次方程组求一次函数表达式的一般步骤： 1.用含字母的系数设出一次函数的表达式：y=kx+b. 2.将已知条件代入上述表达式中，得到关于k、b的二 元一次方程组. 3.解这个二元一次方程组，求得k、b. 4.写出一次函数的表达式. 1.已知一次函数y=kx+5的图象经过点（-1，2）， 则k=______. 2.已知函数y=2x+b的图象经过点（a，7）和（-2，a）， 则这个函数的表达式为____________. 3 y=2x+5 练一练 正比例函数与一次函数的图象如图所示，它们的 交点为A(4，3)，B为一次函数的图象与y轴的交点，且 OA＝2OB.求正比例函数与一次函数的表达式． 解：设正比例函数的表达式为y1＝k1x， 一次函数的表达式为y2＝k2x＋b. ∵点A(4，3)是它们的交点， ∴代入上述表达式中， 得3＝4k1，3＝4k2＋b， ∴k1＝ 即正比例函数的表达式为y＝ x. 3.4 3 4 例4 ∵OA＝ ＝5，且OA＝2OB， ∴OB＝ . ∵点B在y轴的负半轴上， ∴点B的坐标为 又∵点B在一次函数y2＝k2x＋b的图象上， ∴ ＝b. 代入3＝4k2＋b中，得k2＝ . ∴一次函数的表达式为y2＝ x－ . 2 23 4 5 2 50 .2     ， 5- 2 11 8 5 2 11 8 某种拖拉机的油箱可储油40 L，加满油并开始工作 后，油箱中的剩余油量y（L）与工作时间x（h） 之间为一次函数关系，函数图象如图所示. （1）求y关于x的函数表达式； （2）一箱油可供拖拉机工作 几小时？ y = -5x + 40. 8 h 练一练 根据图象确定一次函数的表达式的方法： 从图象上选取两个已知点的坐标，然后运用待 定系数法将两点的横、纵坐标代入所设表达式中求 出待定系数，从而得到函数的表达式． 1.一次函数y=kx+b(k≠0)的图象如图，则下列结论正 确的是 ( ) A．k=2　　B．k=3　　C．b=2　　D．b=3 D y xO 2 3 2. 如图，直线l是一次函数y=kx+b的图象，填空: 　(1)b=______,k=______； (2)当x=30时，y=_____； (3)当y=30时，x=______. 1  2  3  4  5  1 2 3 4 O x y2 2 3  -18 -42 l x y 3.已知一次函数的图象经过(0，5)，(2，－5)两点， 求一次函数的表达式． 解：设一次函数的表达式为y＝kx＋b. 根据题意，得 ∴一次函数的表达式为y＝－5x＋5. 5 5 2 5 5. b k k b b         ， ，解得， 解：设直线l为y=kx+b. 　　∵l与直线y=-2x平行， ∴k= -2. 又∵直线l过点（0，2）， ∴b=2， ∴直线l的表达式为y=-2x+2. 4.已知直线l与直线y=-2x平行，且与y轴交于点(0，2)， 求直线l的表达式. 5.在弹性限度内，弹簧的长度y（厘米）是所挂物体 质量x（千克）的一次函数.一根弹簧不挂物体时长 14.5厘米；当所挂物体的质量为3千克时，弹簧长 16厘米.请写出y与x之间的关系式，并求当所挂物 体的质量为4千克时弹簧的长度. 解：设y=kx+b(k≠0)，则 所以在弹性限度内，y=0.5x+14.5. 当x=4时，y＝0.5×4＋14.5=16.5. 故当所挂物体的质量为4千克时，弹簧的长度为 16.5厘米. 14.5 0.5 3 16 14.5. b k k b b         ， ，解得， 6.已知一次函数的图象过点（0，2），且与两坐标轴 围成的三角形的面积为2，求此一次函数的表达式. 解：设一次函数的表达式为y=kx+b(k≠0). ∵一次函数y=kx+b的图象过点（0，2）， ∴b=2， ∴一次函数的图象与x轴的交点是 ∴ 解得k=1或-1.1 22 2,2 k     2 0k     ， ， ∴此一次函数的表达式为y=x+2或y=-x+2. 用待定系数 法求一次函 数的表达式 2.列：根据已知条件列出关于k、 b的方程组 1. 设：设所求的一次函数表达式 为y=kx+b 3. 解：解方程，求出k、b 4. 代：把求出的k、b代回表达式 即可