华师版数学八年级上册同步课件-第12章-12幂的运算 15页

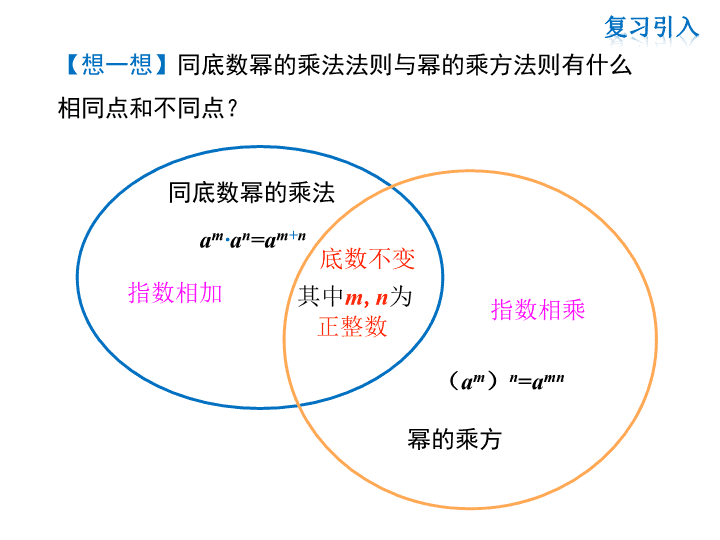
第12章 整式的乘除 12.1 幂的运算 第3课时 积的乘方 1.计算： （1） 10×102× 103 =______ ； （2） (x5 )2=_________.x10 106 2.（1）同底数幂的乘法 ：am·an= ( m，n为正整数)；am+n （2）幂的乘方：(am)n= (m,n为正整数）.amn 底数不变 指数相乘 指数相加 同底数幂的乘法 幂的乘方 其中m,n为 正整数 （am）n=amn am·an=am+n 【想一想】同底数幂的乘法法则与幂的乘方法则有什么 相同点和不同点？ 积的乘方运算 【问题1】下列两题有什么特点？ 2( ) ;a b 3( ) .a b(1) (2) 底数为两个因式相乘，积的形式. 这种形式为 积的乘方。 我们学过的幂的 乘方的运算性质 适用吗？ 1 2( )ab ( ) ( )ab ab  ( ) ( )aa bb  2 2a b 同理： （乘方的意义） （乘法交换律、结合律） （同底数幂相乘的法则） 3( )ab ( ) ( ) ( )ab ab ab   ( ) ( )aa a bbb  3 3a b 【问题2】根据乘方的意义及乘法交换律、结合律进行计算： (ab)n =? (ab) n= (ab)· (ab)· ··· ·(ab) n个ab =(a·a· ··· ·a)·(b·b· ··· ·b) n个a n个b =anbn. 证明： 【思考】积的乘方(ab)n =? 【猜想】 由此可得：(ab)n=anbn (n为正整数). (ab)n=anbn (n为正整数) 这就是说，积的乘方，把积的每一个因式分别 _____，再把所得的幂________. 【想一想】三个或三个以上的积的乘方等于什么？ 乘方 相乘 【例1】 计算： (1) (2a)3 ； (2) (-5b)3 ； (3) (xy2)2 ； (4) (-2x3)4. 解：(1)原式= (2)原式= (3)原式= (4)原式= = 8a3. =-125b3. =x2y4. =16x12. 23·a3 (-5)3·b3 x2·(y2)2 (-2)4·(x3)4 运用积的乘方法则进行计算时，注意每个因式都 要乘方，尤其是字母的系数不要漏乘方． . 4 101 2 4       42 101 2 2           解：原式 8 101 2 2       8 8 21 2 2 2        8 21 2 2 2        .4 【例2】 计算: an·bn = (ab)n am+n =am·an amn =(am)n 注意：逆用积的乘法法则，有时可使运算更加简便快捷！ 积的乘方法则的逆用2 (1)（ab2)3=ab6 ( ) × × × (2) (3xy)3=9x3y3 ( ) ×(3) (-2a2)2=-4a4 ( ) (4) -(-ab2)2=a2b4 ( ) 1.判断： 2.下列运算正确的是（ ） A. x.x2=x2 B. (xy)2=xy2 C.(x2)3=x6 D.x2+x2=x4 C (1) (ab)8 ; (2) (2m)3 ; (3) (-xy)5; (4) (5ab2)3 ; (5) (2×102)2 ; (6) (-3×103)3. 3.计算： 解：(1)原式=a8·b8. (2)原式= 23 ·m3=8m3. (3)原式=(-x)5 ·y5=-x5y5. (4)原式=53 ·a3 ·(b2)3=125a3b6. (5)原式=22×(102)2=4×104. (6)原式=(-3)3 ×(103)3=-27 ×109=-2.7 ×1010. （1) 2(x3)2·x3-(3x3)3+(5x)2·x7; （2）(3xy2)2+(-4xy3) · (-xy) ; （3）(-2x3)3·(x2)2. 解：原式=2x6·x3-27x9+25x2·x7 = 2x9-27x9+25x9 = 0. 解：原式=9x2y4 +4x2y4 =13x2y4. 解：原式= -8x9·x4 =-8x13. 注意：运算顺序 是先乘方，再乘 除，最后加减. 4.计算: 5.如果（an·bm·b)3=a9b15，求m，n的值.  （an）3·（bm）3·b3=a9b15，  a3n ·b3m·b3=a9b15，  a3n ·b3m+3=a9b15，  3n=9，3m+3=15. n=3，m=4. 解：∵（an·bm·b)3=a9b15， 幂的运算 性质 性 质 am·an=am+n (am)n=amn (ab)n=anbn ( m，n为正整数) 逆 用 am+n =am · an amn =(am)n (ab)n= an·bn （可使某些计算简捷） 注 意 公式中的a，b代表任何代数式； 每一个因式都要“乘方”；注意 结果的符号、幂指数及其逆用 （混合运算要注意运算顺序）