2019-2020学年江苏省南京市鼓楼区八年级（下）期末数学试卷 (解析版) 32页

‎2019-2020学年江苏省南京市鼓楼区八年级（下）期末数学试卷 一、选择题 ‎1．化简的结果是（　　）‎ A．﹣2 B．‎2 ‎C．±2 D．4‎ ‎2．若分式有意义，则x的取值范围是（　　）‎ A．x＞1 B．x＝‎1 ‎C．x＜1 D．x≠1‎ ‎3．在下列事件中，是必然事件的是（　　）‎ A．3天内将下雨 ‎ B．367人中至少有2人的生日相同 ‎ C．买一张电影票，座位号是奇数号 ‎ D．在某妇幼保健医院里，下一个出生的婴儿是女孩 ‎4．南京奧林匹克体育中心是亚洲A级体育馆、世界第五代体育建筑的代表，如图是体育馆俯视图的示意图．下列说法正确的是（　　）‎ A．这个图形是轴对称图形，但不是中心对称图形 ‎ B．这个图形是中心对称图形，但不是轴对称图形 ‎ C．这个图形既是中心对称图形，也是轴对称图形 ‎ D．这个图形既不是中心对称图形，也不是轴对称图形 ‎5．已知点P（x1，y1）、Q（x2，y2）在反比例函数y＝﹣的图象上，若y1＜y2＜0，则x1与x2的大小关系是（　　）‎ A．x1＜x2 B．x1＞x‎2 ‎C．x1＝x2 D．无法确定 ‎6．如图，在四边形ABCD中，AD∥BC，AD＝‎6cm，BC＝‎12cm，点P从A出发以lcm/s的速度向D运动，点Q从C出发以‎2cm/s的速度向B运动，两点同时出发，当点P运动到点D时，点Q也随之停止运动．若运动时间为t秒时，以A、B、C、D、P、Q任意四个点为顶点的四边形中同时存在两个平行四边形，则t的值是（　　）‎ A．1 B．‎2 ‎C．3 D．4‎ 二、填空题 ‎7．化简：＝　 　．‎ ‎8．若式子在实数范围内有意义，则x的取值范围是　 　．‎ ‎9．方程（x﹣1）﹣1＝2的解是　 　．‎ ‎10．某种油菜籽在相同条件下发芽试验的结果如表：‎ 每批粒数 ‎50‎ ‎100‎ ‎300‎ ‎400‎ ‎600‎ ‎1000‎ 发芽的频数 ‎45‎ ‎96‎ ‎283‎ ‎380‎ ‎571‎ ‎948‎ 这种油菜籽发芽的概率的估计值是　 　．（结果精确到0.01）‎ ‎11．比较大小：4﹣　 　．（填“＞”、“＜”或“＝”）．‎ ‎12．如图，在△ABC中，∠ACB＝90°，AB＝‎13cm，BC＝‎12cm，点D在边AB上，AD＝AC，AE⊥CD，垂足为E，点F是BC的中点，则EF＝　 　cm．‎ ‎13．如图，在△ABC中，∠C＝90°，△ABC绕点A按顺时针方向旋转26°得到△AED，若AD∥BC，则∠BAE＝　 　°．‎ ‎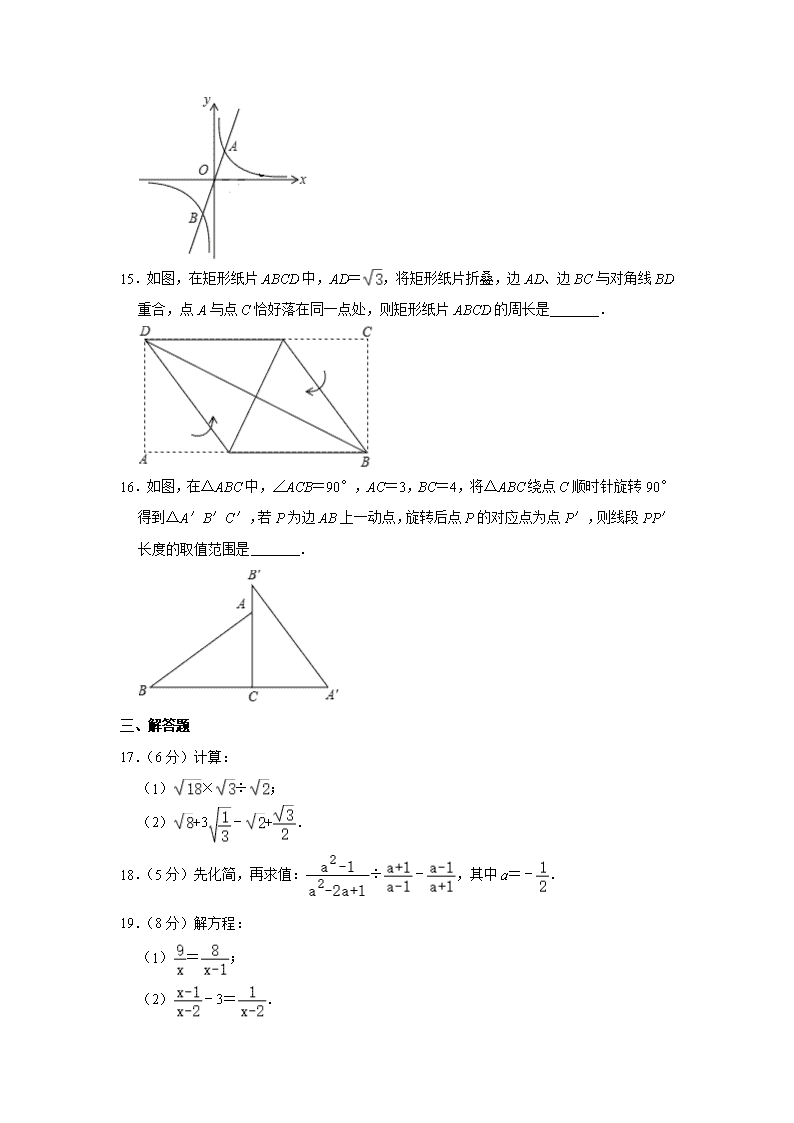14．如图，正比例函数y＝k1x与反比例函数y＝的图象交于点A、B，若点A的坐标为（1，2），则关于x的不等式k1x＞的解集是　 　．‎ ‎15．如图，在矩形纸片ABCD中，AD＝，将矩形纸片折叠，边AD、边BC与对角线BD重合，点A与点C恰好落在同一点处，则矩形纸片ABCD的周长是　 　．‎ ‎16．如图，在△ABC中，∠ACB＝90°，AC＝3，BC＝4，将△ABC绕点C顺时针旋转90°得到△A′B′C′，若P为边AB上一动点，旋转后点P的对应点为点P′，则线段PP′长度的取值范围是　 　．‎ 三、解答题 ‎17．（6分）计算：‎ ‎（1）×÷；‎ ‎（2）+3﹣+．‎ ‎18．（5分）先化简，再求值：÷﹣，其中a＝﹣．‎ ‎19．（8分）解方程：‎ ‎（1）＝；‎ ‎（2）﹣3＝．‎ ‎20．（6分）防疫期间，甲、乙两工厂每小时共做3500个KN95口罩，甲工厂做1600个KN95口罩所用的时间与乙工厂做1200个KN95口罩所用的时间相等．甲、乙两工厂每小时各做多少个KN95口罩？‎ ‎21．（6分）为了调查某校八年级360名学生的身高情况，随机抽取了20名男生与20名女生的身高数据，得到下列图表（图表中身高分组‎153cm～‎158cm表示大于或等于‎153cm而小于‎158cm，其他类同）：‎ 身高分组（cm）‎ 频数 ‎153～158‎ ‎1‎ ‎158～163‎ ‎2‎ ‎163～168‎ ‎6‎ ‎168～173‎ ‎7‎ ‎173～178‎ ‎3‎ ‎178～183‎ ‎1‎ ‎（1）写出本次调查的总体与样本：　 　；‎ ‎（2）根据调查结果，绘制抽取的40名学生的身高频数分布直方图；‎ ‎（3）估计该校八年级学生身高在‎163cm～‎183cm范围内的学生人数．‎ ‎22．（5分）已知∠MAN，按要求完成下列尺规作图（不写作法，保留作图痕迹）．‎ ‎（1）如图①，B，C分别在射线AM、AN上，求作▱ABDC；‎ ‎（2）如图②，点O是∠MAN内一点，求作线段PQ，使P、Q分别在射线AM、AN上，且点O是PQ的中点．‎ ‎23．（7分）在5×5的方格纸中，每个小正方形的边长为1，我们把三个顶点都是格点的三角形称为格点三角形，按要求完成下列问题：‎ ‎（1）在图①中，以AB为边画一个格点三角形，使其为等腰三角形；‎ ‎（2）在图②中，以AB为边画一个格点三角形，使其为钝角三角形且周长为6+3；‎ ‎（3）如图③，若以AB为边的格点三角形的面积为3，则这个三角形的周长为　 　．‎ ‎24．（8分）如图，在菱形ABCD中，点O是对角线AC的中点，过点O的直线EF与边AD、BC交于点E、F，∠CAE＝∠FEA，连接AF、CE．‎ ‎（1）求证：四边形AFCE是矩形；‎ ‎（2）若AB＝5，AC＝2，直接写出四边形AFCE的面积．‎ ‎25．（8分）如图，点A，B是反比例函数y＝的图象上的两个动点，过A、B分别作AC⊥x轴、BD⊥x轴，分别交反比例函数y＝﹣的图象于点C、D，四边形ACBD是平行四边形．‎ ‎（1）若点A的横坐标为﹣4．‎ ‎①直接写出线段AC的长度；‎ ‎②求出点B的坐标；‎ ‎（2）当点A、B不断运动时，下列关于▱ACBD的结论：①▱ACBD可能是矩形；②▱ACBD可能是菱形；③▱ACBD可能是正方形；④▱ACBD的周长始终不变；⑤▱ACBD的面积始终不变．其中所有正确结论的序号是　 　．‎ ‎26．（9分）已知，四边形ABCD是正方形，点E是正方形ABCD所在平面内一动点（不与点D重合），AB＝AE，过点B作DE的垂线交DE所在直线于点F，连接CF．‎ 提出问题：当点E运动时，线段CF与线段DE之间的数量关系是否发生变化？‎ 探究问题：‎ ‎（1）首先考察点E的一个特殊位置：当点E与点B重合（如图①时），点F与点B 也重合．用等式表示线段CF与线段DE之间的数量关系：　 　．‎ ‎（2）然后考察点E的一般位置，分两种情况：‎ 情况1：当点E是正方形ABCD内部一点（如图②时）；‎ 情况2：当点E是正方形ABCD外部一点（如图③时）．‎ 在情况1或情况2下，线段CF与线段DE之间的数量关系与（1）中结论是否相同？如果都相同，请选择一种情况证明；如果只在一种情况下相同或在两种情况下都不相同，请说明理由；‎ 拓展问题：‎ ‎（3）连接AF，用等式表示线段AF、CF、DF三者之间的数量关系：　 　．‎ ‎2019-2020学年江苏省南京市鼓楼区八年级（下）期末数学试卷 参考答案与试题解析 一、选择题 ‎1．化简的结果是（　　）‎ A．﹣2 B．‎2 ‎C．±2 D．4‎ ‎【分析】由于表示4的算术平方根，根据算术平方根的定义即可求出结果．‎ ‎【解答】解：∵2的平方是4，‎ ‎∴4算术平方根为2．‎ 故选：B．‎ ‎2．若分式有意义，则x的取值范围是（　　）‎ A．x＞1 B．x＝‎1 ‎C．x＜1 D．x≠1‎ ‎【分析】根据分式有意义，分母不等于0列不等式求解即可．‎ ‎【解答】解：由题意得，x﹣1≠0，‎ 解得x≠1．‎ 故选：D．‎ ‎3．在下列事件中，是必然事件的是（　　）‎ A．3天内将下雨 ‎ B．367人中至少有2人的生日相同 ‎ C．买一张电影票，座位号是奇数号 ‎ D．在某妇幼保健医院里，下一个出生的婴儿是女孩 ‎【分析】必然事件就是一定发生的事件，即发生的概率是1的事件．‎ ‎【解答】解：A．3天内将下雨是随机事件；‎ B．367人中至少有2人的生日相同是必然事件；‎ C．买一张电影票，座位号是奇数号是随机事件；‎ D．在某妇幼保健医院里，下一个出生的婴儿是女孩是随机事件；‎ 故选：B．‎ ‎4．南京奧林匹克体育中心是亚洲A级体育馆、世界第五代体育建筑的代表，如图是体育馆俯视图的示意图．下列说法正确的是（　　）‎ A．这个图形是轴对称图形，但不是中心对称图形 ‎ B．这个图形是中心对称图形，但不是轴对称图形 ‎ C．这个图形既是中心对称图形，也是轴对称图形 ‎ D．这个图形既不是中心对称图形，也不是轴对称图形 ‎【分析】根据中心对称图形和轴对称图形对各选项分析判断即可得解．‎ ‎【解答】解：这个图形既是中心对称图形，也是轴对称图形．‎ 故选：C．‎ ‎5．已知点P（x1，y1）、Q（x2，y2）在反比例函数y＝﹣的图象上，若y1＜y2＜0，则x1与x2的大小关系是（　　）‎ A．x1＜x2 B．x1＞x‎2 ‎C．x1＝x2 D．无法确定 ‎【分析】根据反比例函数图象性质可得k＝﹣1＜0，图象过第二、四象限，进而可以得出当y1＜y2＜0时x1与x2的大小关系．‎ ‎【解答】解：∵反比例函数y＝﹣的图象过第二、四象限，‎ 当y1＜y2＜0时，‎ 则x1＜x2，‎ 故选：A．‎ ‎6．如图，在四边形ABCD中，AD∥BC，AD＝‎6cm，BC＝‎12cm，点P从A出发以lcm/s的速度向D运动，点Q从C出发以‎2cm/s的速度向B运动，两点同时出发，当点P运动到点D时，点Q也随之停止运动．若运动时间为t秒时，以A、B、C、D、P、Q任意四个点为顶点的四边形中同时存在两个平行四边形，则t的值是（　　）‎ A．1 B．‎2 ‎C．3 D．4‎ ‎【分析】根据题意计算AP、PD、BQ、CQ，再根据平行四边形的判定方法进行判定．‎ ‎【解答】解：A．t＝1时，AP＝‎1cm，PD＝‎5cm，CQ＝‎2cm，BQ＝‎10cm，此时构不成平行四边形，不符合题意；‎ B．t＝2时，AP＝‎2cm，PD＝‎4cm，CQ＝‎4cm，BQ＝‎8cm，因AD∥BC，此时只构成一个平行四边形PDCQ，不符合题意；‎ C．t＝3时，AP＝PD＝‎3cm，CQ＝BQ＝‎6cm，则CQ＝BQ＝AD，因AD∥BC，此时有2个平行四边形：平行四边形ADCQ和平行四边形ADQB，符合题意；‎ D．t＝4时，AP＝‎4cm，PD＝‎2cm，CQ＝‎8cm，BQ＝‎4cm，因AD∥BC，此时只构成一个平行四边形APQB，不符合题意．‎ 故选：C．‎ 二、填空题 ‎7．化简：＝　　．‎ ‎【分析】直接利用分式的性质化简得出答案．‎ ‎【解答】解：＝．‎ 故答案为：．‎ ‎8．若式子在实数范围内有意义，则x的取值范围是　x≥2　．‎ ‎【分析】根据被开方数是非负数，可得答案．‎ ‎【解答】解：由题意，得 x﹣2≥0，‎ 解得x≥2，‎ 故答案为：x≥2．‎ ‎9．方程（x﹣1）﹣1＝2的解是　x＝　．‎ ‎【分析】先将原方程转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解；‎ ‎【解答】解：将原方程式转化为整式方程为：‎ ‎﹣2x+3＝0，‎ 解得：x＝，‎ 经检验x＝是原分式方程的解；‎ 故答案为：x＝．‎ ‎10．某种油菜籽在相同条件下发芽试验的结果如表：‎ 每批粒数 ‎50‎ ‎100‎ ‎300‎ ‎400‎ ‎600‎ ‎1000‎ 发芽的频数 ‎45‎ ‎96‎ ‎283‎ ‎380‎ ‎571‎ ‎948‎ 这种油菜籽发芽的概率的估计值是　0.95　．（结果精确到0.01）‎ ‎【分析】利用大量重复试验下事件发生的频率可以估计该事件发生的概率直接回答即可．‎ ‎【解答】解：观察表格得到这种油菜籽发芽的频率稳定在0.95附近，‎ 则这种油菜籽发芽的概率的估计值是0.95，‎ 故答案为：0.95．‎ ‎11．比较大小：4﹣　＜　．（填“＞”、“＜”或“＝”）．‎ ‎【分析】因为≈3.6056，所以4﹣＜0.5＝，由此即可求解．‎ ‎【解答】解：因为≈3.6056，＝0.5，‎ 所以4﹣＜，‎ 故答案为：＜．‎ ‎12．如图，在△ABC中，∠ACB＝90°，AB＝‎13cm，BC＝‎12cm，点D在边AB上，AD＝AC，AE⊥CD，垂足为E，点F是BC的中点，则EF＝　‎4　cm．‎ ‎【分析】根据勾股定理求出AC，得到BD的长，根据等腰三角形的性质得到CE＝DE，根据三角形中位线定理解答即可．‎ ‎【解答】解：在△ABC中，∠ACB＝90°，‎ ‎∴AC＝＝＝5，‎ ‎∴AD＝AC＝5，‎ ‎∴BD＝AB﹣AD＝13﹣5＝8，‎ ‎∵AC＝AD，AE⊥CD，‎ ‎∴CE＝DE，‎ ‎∵CE＝DE，CF＝BF，‎ ‎∴EF是△CBD的中位线，‎ ‎∴EF＝BD＝4，‎ 故答案为：4．‎ ‎13．如图，在△ABC中，∠C＝90°，△ABC绕点A按顺时针方向旋转26°得到△AED，若AD∥BC，则∠BAE＝　38　°．‎ ‎【分析】由旋转的性质可得∠DAB＝∠EAC＝26°，由平行线的性质可得∠B＝∠DAB＝26°，由直角三角形的性质可得∠BAC＝64°，即可求解．‎ ‎【解答】解：∵△ABC绕点A按顺时针方向旋转26°得到△AED，‎ ‎∴∠DAB＝∠EAC＝26°，‎ ‎∵AD∥BC，‎ ‎∴∠B＝∠DAB＝26°，‎ ‎∵∠C＝90°，‎ ‎∴∠BAC＝64°，‎ ‎∴∠BAE＝∠BAC﹣∠EAC＝64°﹣26°＝38°，‎ 故答案为：38°．‎ ‎14．如图，正比例函数y＝k1x与反比例函数y＝的图象交于点A、B，若点A的坐标为（1，2），则关于x的不等式k1x＞的解集是　﹣1＜x＜0或x＞1　．‎ ‎【分析】先利用正比例函数图象和反比例函数图象的性质得正比例函数y＝k1x与反比例函数y＝的图象的另一个交点坐标为（﹣1，﹣2），然后利用函数图象，写出一次函数图象在反比例函数图象上方所对应的自变量的范围即可．‎ ‎【解答】解：∵正比例函数y＝k1x与反比例函数y＝的图象交于点A（1，2），‎ ‎∴正比例函数y＝k1x与反比例函数y＝的图象的另一个交点坐标为（﹣1，﹣2），‎ ‎∴不等式k1x＞的解集为﹣1＜x＜0或x＞1．‎ 故答案为﹣1＜x＜0或x＞1．‎ ‎15．如图，在矩形纸片ABCD中，AD＝，将矩形纸片折叠，边AD、边BC与对角线BD重合，点A与点C恰好落在同一点处，则矩形纸片ABCD的周长是　6+2　．‎ ‎【分析】由题意BD＝2AD＝2，利用勾股定理求出AB即可解决问题．‎ ‎【解答】解：∵四边形ABCD是矩形，‎ ‎∴∠A＝90°，AD＝BC＝，AB＝CD，‎ 由翻折的性质可知，BD＝2AD＝2，‎ ‎∴AB＝CD＝＝＝3，‎ ‎∴四边形ABCD的周长为6+2，‎ 故答案为6+2．‎ ‎16．如图，在△ABC中，∠ACB＝90°，AC＝3，BC＝4，将△ABC绕点C顺时针旋转90°得到△A′B′C′，若P为边AB上一动点，旋转后点P的对应点为点P′，则线段PP′‎ 长度的取值范围是　≤PP'≤4　．‎ ‎【分析】过点C作CH⊥AB于H，由勾股定理可求AB的长，由三角形面积公式可求CH的长，由旋转的性质可得PC＝P'C，∠PCP'＝90°，可得PP'＝CP，则当点P与点B重合时，CP有最大值为4，当点P与点H重合时，CP有最小值为，即可求解．‎ ‎【解答】解：如图，过点C作CH⊥AB于H，‎ ‎∵∠ACB＝90°，AC＝3，BC＝4，‎ ‎∴AB＝＝＝5，‎ ‎∵S△ABC＝×3×4＝×5×CH，‎ ‎∴CH＝，‎ ‎∵将△ABC绕点C顺时针旋转90°得到△A′B′C′，‎ ‎∴PC＝P'C，∠PCP'＝90°，‎ ‎∴PP'＝CP，‎ ‎∵P为边AB上一动点，‎ ‎∴当点P与点B重合时，CP有最大值为4，当点P与点H重合时，CP有最小值为，‎ ‎∴≤PP'≤4，‎ 故答案为：≤PP'≤4．‎ 三、解答题 ‎17．（6分）计算：‎ ‎（1）×÷；‎ ‎（2）+3﹣+．‎ ‎【分析】（1）利用二次根式的乘除法则运算；‎ ‎（2）先把二次根式化为最简二次根式，然后合并即可．‎ ‎【解答】解：（1）原式＝‎ ‎＝3；‎ ‎（2）原式＝2+﹣+‎ ‎＝+．‎ ‎18．（5分）先化简，再求值：÷﹣，其中a＝﹣．‎ ‎【分析】先把除法变成乘法，算乘法，再算减法，最后代入求出即可．‎ ‎【解答】解：原式＝﹣‎ ‎＝1﹣‎ ‎＝‎ ‎＝，‎ 当a＝﹣时，原式＝＝4．‎ ‎19．（8分）解方程：‎ ‎（1）＝；‎ ‎（2）﹣3＝．‎ ‎【分析】两分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．‎ ‎【解答】解：（1）方程两边同乘x（x﹣1）得：‎ ‎9（x﹣1）＝8x，‎ 解得：x＝9，‎ 经检验x＝9是分式方程的解；‎ ‎（2）方程两边同乘x﹣2得：‎ x﹣1﹣3（x﹣2）＝1，‎ 解得：x＝2，‎ 经检验x＝2是增根，分式方程无解．‎ ‎20．（6分）防疫期间，甲、乙两工厂每小时共做3500个KN95口罩，甲工厂做1600个KN95口罩所用的时间与乙工厂做1200个KN95口罩所用的时间相等．甲、乙两工厂每小时各做多少个KN95口罩？‎ ‎【分析】设甲工厂每小时做x个KN95口罩，则乙工厂每小时做（3500﹣x）个KN95口罩，根据工作时间＝工作总量÷工作效率结合甲工厂做1600个KN95口罩所用的时间与乙工厂做1200个KN95口罩所用的时间相等，即可得出关于x的分式方程，此题得解．‎ ‎【解答】解：设甲工厂每小时做x个KN95口罩，则乙工厂每小时做（3500﹣x）个KN95口罩，‎ 由题意得：，‎ 解得：x＝2000，‎ 经检验：x＝2000是原分式方程的解，‎ 则3500﹣2000＝1500（个）．‎ 答：甲工厂每小时做2000个KN95口罩，则乙工厂每小时做1500个KN95口罩．‎ ‎21．（6分）为了调查某校八年级360名学生的身高情况，随机抽取了20名男生与20名女生的身高数据，得到下列图表（图表中身高分组‎153cm～‎158cm表示大于或等于‎153cm而小于‎158cm，其他类同）：‎ 身高分组（cm）‎ 频数 ‎153～158‎ ‎1‎ ‎158～163‎ ‎2‎ ‎163～168‎ ‎6‎ ‎168～173‎ ‎7‎ ‎173～178‎ ‎3‎ ‎178～183‎ ‎1‎ ‎（1）写出本次调查的总体与样本：　总体：某校八年级360名学生的身高情况的全体；‎ 样本：抽取的20名男生与20名女生的身高情况　；‎ ‎（2）根据调查结果，绘制抽取的40名学生的身高频数分布直方图；‎ ‎（3）估计该校八年级学生身高在‎163cm～‎183cm范围内的学生人数．‎ ‎【分析】（1）根据总体、样本的意义，结合具体问题情境教学回答即可，‎ ‎（2）计算女生的各个段的频数，即可补全频数分布直方图，‎ ‎（3）求360人的40%即可．‎ ‎【解答】解：（1）总体：某校八年级360名学生的身高情况的全体；‎ 样本：抽取的20名男生与20名女生的身高情况；‎ 故答案为：总体：某校八年级360名学生的身高情况的全体，样本：抽取的20名男生与20名女生的身高情况；‎ ‎（2）20×10%＝2（名），20×20%＝4（名），20×40%＝8（名），‎ 各身高段的频数为：‎ 绘制抽取的40名学生的身高频数分布直方图；‎ ‎（3）360×＝279（名），‎ 答：该校八年级学生身高在‎163cm～‎183cm范围内的学生人数为279人．‎ ‎22．（5分）已知∠MAN，按要求完成下列尺规作图（不写作法，保留作图痕迹）．‎ ‎（1）如图①，B，C分别在射线AM、AN上，求作▱ABDC；‎ ‎（2）如图②，点O是∠MAN内一点，求作线段PQ，使P、Q分别在射线AM、AN上，且点O是PQ的中点．‎ ‎【分析】（1）分别以B、C点为圆心，以AC、AB为半径画弧．两弧相交于点D，则四边形ABDC满足条件；‎ ‎（2）连接AO，延长AO到G使OG＝AO，再作∠PGA＝∠OAN交AM于P，连接PO并延长交AN于Q，则PQ满足条件．‎ ‎【解答】解：（1）如图①，平行四边形ABCD为所作；‎ ‎（2）如图②，PQ为所作．‎ ‎23．（7分）在5×5的方格纸中，每个小正方形的边长为1，我们把三个顶点都是格点的三角形称为格点三角形，按要求完成下列问题：‎ ‎（1）在图①中，以AB为边画一个格点三角形，使其为等腰三角形；‎ ‎（2）在图②中，以AB为边画一个格点三角形，使其为钝角三角形且周长为6+3；‎ ‎（3）如图③，若以AB为边的格点三角形的面积为3，则这个三角形的周长为　2++3或4+2或2+3+　．‎ ‎【分析】（1）利用网格在图①中，以AB为边画格点三角形，使其为等腰三角形即可；‎ ‎（2）利用网格在图②中，以AB为边画格点三角形，使其为钝角三角形且周长为6+3即可；‎ ‎（3）利用网格在图③中，以AB为边的格点三角形的面积为3，即可求出这个三角形的周长．‎ ‎【解答】解：（1）如图①所示：△ABC1、△ABC2、△ABC3、△ABC4 即为所求；‎ ‎（2）如图②所示：△ABC1、△ABC2 即为所求；‎ 两个三角形为钝角三角形且周长为6+3；‎ ‎（3）如图③所示：以AB为边的格点三角形的面积为3，‎ 则这个三角形的周长为：2++3、4+2、2+3+．‎ 故答案为：2++3、4+2、2+3+．‎ ‎24．（8分）如图，在菱形ABCD中，点O是对角线AC的中点，过点O的直线EF与边AD、BC交于点E、F，∠CAE＝∠FEA，连接AF、CE．‎ ‎（1）求证：四边形AFCE是矩形；‎ ‎（2）若AB＝5，AC＝2，直接写出四边形AFCE的面积．‎ ‎【分析】（1）求出OA＝OE＝OC＝OF，根据平行四边形的判定得出四边形AFCE是平行四边形，再根据矩形的判定得出即可；‎ ‎（2）根据勾股定理得出AF2＝AB2﹣BF2＝AC2﹣CF2，即52﹣（5﹣x）2＝（2）2﹣x2，求出x，即得出CF＝4，根据勾股定理求出AF，再求出矩形AFCE的面积即可．‎ ‎【解答】（1）证明：∵∠OAE＝∠OEA，‎ ‎∴OA＝OE，‎ ‎∵四边形ABCD是菱形，‎ ‎∴AD∥BC，‎ ‎∴∠OCF＝∠OAE，∠OFC＝∠OEA，‎ ‎∴∠OFC＝∠OCF，‎ ‎∵OF＝OC，‎ ‎∵O为AC的中点，‎ ‎∴OA＝OC，‎ ‎∴OA＝OC＝OE＝OF，‎ ‎∴四边形AFCE是平行四边形，AC＝EF，‎ ‎∴四边形AFCE是矩形；‎ ‎（2）解：设CF＝x，‎ ‎∵四边形ABCD是菱形，AB＝5，‎ ‎∴BC＝AB＝5，‎ ‎∴BF＝5﹣x，‎ ‎∵四边形AFCE是矩形，‎ ‎∴∠AFC＝90°＝∠AFB，‎ 在Rt△AFB和Rt△AFC中，由勾股定理得：AF2＝AB2﹣BF2＝AC2﹣CF2，‎ 即52﹣（5﹣x）2＝（2）2﹣x2，‎ 解得：x＝4，‎ 即CF＝4，‎ 则AF＝＝＝2，‎ ‎∴四边形AFCE的面积是AF×CF＝2×4＝8．‎ ‎25．（8分）如图，点A，B是反比例函数y＝的图象上的两个动点，过A、B分别作AC⊥x轴、BD⊥x轴，分别交反比例函数y＝﹣的图象于点C、D，四边形ACBD是平行四边形．‎ ‎（1）若点A的横坐标为﹣4．‎ ‎①直接写出线段AC的长度；‎ ‎②求出点B的坐标；‎ ‎（2）当点A、B不断运动时，下列关于▱ACBD的结论：①▱ACBD可能是矩形；②▱ACBD可能是菱形；③▱ACBD可能是正方形；④▱ACBD的周长始终不变；⑤▱ACBD的面积始终不变．其中所有正确结论的序号是　②⑤　．‎ ‎【分析】（1）①根据A点的横坐标分别求得A、C两点的坐标，进而得AC；‎ ‎②设B点坐标为（t，），则D点坐标为（t，﹣），根据AC＝BD列出t的方程求出t，便可求得B点坐标；‎ ‎（2）设A（a，），B（b，），则C（a，﹣），D（b，﹣），由平行四边形的性质AC＝BD列出方程求得a、b的关系，进而得B、C的坐标，根据坐标可以判断BC不与x轴平行，从而判断AC与BD垂直，进而判断①、③错误；根据随着|a|不断变小，AC起来越大，BC起来越小，可以判断AC有可能与BC相等，进而判断②的正误；根据a的两个特殊值，计算出▱ACBD的两个周长不相等，从而判断④的正误；计算出AC与BD间的距离，再根据平行四边形的面积公式计算出面积，便可判断⑤的正误．‎ ‎【解答】解：（1）①把x＝﹣4代入中，得y＝﹣2，‎ ‎∴A（﹣4，﹣2），‎ 把x＝﹣4代入中，得y＝，‎ ‎∴，‎ ‎∴；‎ ‎②∵四边形ABCD是平行四边形，‎ ‎∴BD＝AC＝，‎ 设B点坐标为（t，），则D点坐标为（t，﹣），‎ 则，‎ 解得，t＝4，‎ ‎∴B（4，2）；‎ ‎（2）设A（a，），B（b，），则C（a，﹣），D（b，﹣），‎ ‎∵AC＝BD，‎ ‎∴，‎ ‎∴a＝﹣b，‎ ‎∴，‎ ‎∴AC与BC不可能垂直，‎ 故①、③错误；‎ ‎∵随着|a|不断变小，AC起来越大，BC起来越小，‎ ‎∴AC有可能与BC相等，‎ 故②正确；‎ 当a＝﹣1时，▱ACBD的周长＝2（AC+BC）＝2（10+2）＝20+4，‎ 当a＝﹣2时，▱ACBD的周长＝2（AC+BC）＝2（5+2）＝10+4，‎ ‎∵两个▱ACBD的周长不相等，‎ ‎∴④错误；‎ ‎∵BD＝，AC、BD之间的距离为b﹣a＝b﹣（﹣b）＝2b，‎ ‎∴，‎ 故⑤正确，‎ 综上，本题的正确答案是②⑤．‎ 故答案为②⑤．‎ ‎26．（9分）已知，四边形ABCD是正方形，点E是正方形ABCD所在平面内一动点（不与点D重合），AB＝AE，过点B作DE的垂线交DE所在直线于点F，连接CF．‎ 提出问题：当点E运动时，线段CF与线段DE之间的数量关系是否发生变化？‎ 探究问题：‎ ‎（1）首先考察点E的一个特殊位置：当点E与点B重合（如图①时），点F与点B也重合．用等式表示线段CF与线段DE之间的数量关系：　DE＝CF　．‎ ‎（2）然后考察点E的一般位置，分两种情况：‎ 情况1：当点E是正方形ABCD内部一点（如图②时）；‎ 情况2：当点E是正方形ABCD外部一点（如图③时）．‎ 在情况1或情况2下，线段CF与线段DE之间的数量关系与（1）中结论是否相同？如果都相同，请选择一种情况证明；如果只在一种情况下相同或在两种情况下都不相同，请说明理由；‎ 拓展问题：‎ ‎（3）连接AF，用等式表示线段AF、CF、DF三者之间的数量关系：　AF+CF＝DF或AF﹣CF＝DF或CF﹣AF＝DF　．‎ ‎【分析】（1）易证△BCD是等腰直角三角形，得出DB＝CB，即可得出结果；‎ ‎（2）情况1：过点C作CG⊥CF，交DF于G，设BC交DF于P，由ASA证得△CDG≌△CBF，得出DG＝FB，CG＝CF，则△GCF是等腰直角三角形，FG＝CF，连接BE，设∠CDG＝α，则∠CBF＝α，∠DEA＝∠ADE＝90°﹣α，求出∠DAE＝2α，则∠EAB＝90°﹣2α，∠BEA＝∠ABE＝（180°﹣∠EAB）＝45°+α，∠CBE＝45°﹣α，推出∠FBE＝45°，得出△BEF是等腰直角三角形，则EF＝BF，推出EF＝DG，DE＝FG，得出DE＝CF；‎ 情况2：过点C作CG⊥CF交DF延长线于G，连接BE，设CD交BF于P，由ASA证得△CDG≌△CBF，得出DG＝FB，CG＝CF，则△GCF是等腰直角三角形，得FG＝CF，设∠CDG＝α，则∠CBF＝α，证明△BEF是等腰直角三角形，得出EF＝BF，推出DE ‎＝FG，得出DE＝CF；‎ ‎（3）①当F在BC的右侧时，作HD⊥DF交FA延长线于H，由（2）得△BEF是等腰直角三角形，EF＝BF，由SSS证得△ABF≌△AEF，得出∠EFA＝∠BFA＝∠BFE＝45°，则△HDF是等腰直角三角形，得HF＝DF，DH＝DF，∵∠HDF＝∠ADC＝90°，由SAS证得△HDA≌△FDC，得CF＝HA，即可得出AF+CF＝DF；‎ ‎②当F在AB的下方时，作DH⊥DE，交FC延长线于H，在DF上取点N，使CN＝CD，连接BN，证明△BFN是等腰直角三角形，得BF＝NF，由SSS证得△CNF≌△CBF，得∠NFC＝∠BFC＝∠BFD＝45°，则△DFH是等腰直角三角形，得FH＝DF，DF＝DH，由SAS证得△ADF≌△CDH，得出CH＝AF，即可得出AF+CF＝DF；‎ ‎③当F在DC的上方时，连接BE，作HD⊥DF，交AF于H，由（2）得△BEF是等腰直角三角形，EF＝BF，由SSS证得△ABF≌△AEF，得∠EFA＝∠BFA＝∠BFE＝45°，则△HDF是等腰直角三角形，得出HF＝DF，DH＝DF，由SAS证得△ADC≌△HDF，得出AH＝CF，即可得出AF﹣CF＝DF；‎ ‎④当F在AD左侧时，作HD⊥DF交AF的延长线于H，连接BE，设AD交BF于P，证明△BFE是等腰直角三角形，得EF＝BF，由SSS证得△ABF≌△AEF，得∠EFA＝∠BFA＝∠BFE＝45°，则∠DFH＝∠EFA＝45°，△HDF是等腰直角三角形，得DH＝DF，HF＝DF，由SAS证得△HDA≌△FDC，得出AF＝CF，即可得出CF﹣AF＝DF．‎ ‎【解答】解：（1）∵四边形ABCD是正方形，‎ ‎∴CD＝CB，∠BCD＝90°，‎ ‎∴△BCD是等腰直角三角形，‎ ‎∴DB＝CB，‎ 当点E、F与点B重合时，则DE＝CF，‎ 故答案为：DE＝CF；‎ ‎（2）在情况1或情况2下，线段CF与线段DE之间的数量关系与（1）中结论相同；理由如下：‎ 情况1：∵四边形ABCD是正方形，‎ ‎∴CD＝CB＝AD＝AB＝AE，∠BCD＝∠DAB＝∠ABC＝90°，‎ 过点C作CG⊥CF，交DF于G，如图②所示：‎ 则∠BCD＝∠GCF＝90°，‎ ‎∴∠DCG＝∠BCF，‎ 设BC交DF于P，‎ ‎∵BF⊥DE，‎ ‎∴∠BFD＝∠BCD＝90°，‎ ‎∵∠DPC＝∠FPB，‎ ‎∴∠CDP＝∠FBP，‎ 在△CDG和△CBF中，，‎ ‎∴△CDG≌△CBF（ASA），‎ ‎∴DG＝FB，CG＝CF，‎ ‎∴△GCF是等腰直角三角形，‎ ‎∴FG＝CF，‎ 连接BE，‎ 设∠CDG＝α，则∠CBF＝α，∠ADE＝90°﹣α，‎ ‎∵AD＝AE，‎ ‎∴∠DEA＝∠ADE＝90°﹣α，‎ ‎∴∠DAE＝180°﹣2（90°﹣α）＝2α，‎ ‎∴∠EAB＝90°﹣2α，‎ ‎∵AB＝AE，‎ ‎∴∠BEA＝∠ABE＝（180°﹣∠EAB）＝（180°﹣90°+2α）＝45°+α，‎ ‎∴∠CBE＝90°﹣（45°+α）＝45°﹣α，‎ ‎∴∠FBE＝∠CBE+∠CBF＝45°﹣α+α＝45°，‎ ‎∵BF⊥DE，‎ ‎∴△BEF是等腰直角三角形，‎ ‎∴EF＝BF，‎ ‎∴EF＝DG，‎ ‎∴EF+EG＝DG+EG，即DE＝FG，‎ ‎∴DE＝CF；‎ 情况2：过点C作CG⊥CF交DF延长线于G，连接BE，设CD交BF于P，如图③所示：‎ ‎∵∠GCF＝∠BCD＝90°，‎ ‎∴∠DCG＝∠BCF，‎ ‎∵∠FPD＝∠BPC，‎ ‎∴∠FDP＝∠PBC，‎ 在△CDG和△CBF中，，‎ ‎∴△CDG≌△CBF（ASA），‎ ‎∴DG＝FB，CG＝CF，‎ ‎∴△GCF是等腰直角三角形，‎ ‎∴FG＝CF，‎ 设∠CDG＝α，则∠CBF＝α，‎ 同理可知：∠DEA＝∠ADE＝90°﹣α，∠DAE＝2α，‎ ‎∴∠EAB＝90°+2α，‎ ‎∵AB＝AE，‎ ‎∴∠BEA＝∠ABE＝45°﹣α，‎ ‎∴∠FEB＝∠DEA﹣∠AEB＝90°﹣α﹣（45°﹣α）＝45°，‎ ‎∵BF⊥DE，‎ ‎∴△BEF是等腰直角三角形，‎ ‎∴EF＝BF，‎ ‎∴EF＝DG，‎ ‎∴DE＝FG，‎ ‎∴DE＝CF；‎ ‎（3）①当F在BC的右侧时，作HD⊥DF交FA延长线于H，如图④所示：‎ 由（2）得：△BEF是等腰直角三角形，EF＝BF，‎ 在△ABF和△AEF中，，‎ ‎∴△ABF≌△AEF（SSS），‎ ‎∴∠EFA＝∠BFA＝∠BFE＝45°，‎ ‎∴△HDF是等腰直角三角形，‎ ‎∴HF＝DF，DH＝DF，‎ ‎∵∠HDF＝∠ADC＝90°，‎ ‎∴∠HDA＝∠FDC，‎ 在△HDA和△FDC中，，‎ ‎∴△HDA≌△FDC（SAS），‎ ‎∴CF＝HA，‎ ‎∴DF＝HF＝HA+AF＝CF+AF，即AF+CF＝DF；‎ ‎②当F在AB的下方时，作DH⊥DE，交FC延长线于H，在DF上取点N，使CN＝CD，连接BN，如图⑤所示：‎ 设∠DAE＝α，则∠CDN＝∠CND＝90°﹣α，‎ ‎∴∠DCN＝2α，‎ ‎∴∠NCB＝90°﹣2α，‎ ‎∵CN＝CD＝CB，‎ ‎∴∠CNB＝∠CBN＝（180°﹣∠NCB）＝（180°﹣90°+2α）＝45°+α，‎ ‎∵∠CNE＝180°﹣∠CND＝180°﹣（90°﹣α）＝90°+α，‎ ‎∴∠FNB＝90°+α﹣（45°+α）＝45°，‎ ‎∴△BFN是等腰直角三角形，‎ ‎∴BF＝NF，‎ 在△CNF和△CBF中，，‎ ‎∴△CNF≌△CBF（SSS），‎ ‎∴∠NFC＝∠BFC＝∠BFD＝45°，‎ ‎∴△DFH是等腰直角三角形，‎ ‎∴FH＝DF，DF＝DH，‎ ‎∵∠ADC＝∠HDE＝90°，‎ ‎∴∠ADF＝∠CDH，‎ 在△ADF和△CDH中，‎ ‎，‎ ‎∴△ADF≌△CDH（SAS），‎ ‎∴CH＝AF，‎ ‎∴FH＝CH+CF＝AF+CF，‎ ‎∴AF+CF＝DF；‎ ‎③当F在DC的上方时，连接BE，作HD⊥DF，交AF于H，如图⑥所示：‎ 由（2）得：△BEF是等腰直角三角形，EF＝BF，‎ 在△ABF和△AEF中，‎ ‎，‎ ‎∴△ABF≌△AEF（SSS），‎ ‎∴∠EFA＝∠BFA＝∠BFE＝45°，‎ ‎∴△HDF是等腰直角三角形，‎ ‎∴HF＝DF，DH＝DF，‎ ‎∵∠ADC＝∠HDF＝90°，‎ ‎∴∠ADH＝∠CDF，‎ 在△ADC和△HDF中，，‎ ‎∴△ADC≌△HDF（SAS），‎ ‎∴AH＝CF，‎ ‎∴HF＝AF﹣AH＝AF﹣CF，‎ ‎∴AF﹣CF＝DF；‎ ‎④当F在AD左侧时，作HD⊥DF交AF的延长线于H，连接BE，设AD交BF于P，如图⑦所示：‎ ‎∵AB＝AE＝AD，‎ ‎∴∠AED＝∠ADE，‎ ‎∵∠PFD＝∠PAB＝90°，∠FPD＝∠BPA，‎ ‎∴∠ABP＝∠FDP，‎ ‎∴∠FEA＝∠FBA，‎ ‎∵AB＝AE，‎ ‎∴∠AEB＝∠ABE，‎ ‎∴∠FEB＝∠FBE，‎ ‎∴△BFE是等腰直角三角形，‎ ‎∴EF＝BF，‎ 在△ABF和△AEF中，‎ ‎，‎ ‎∴△ABF≌△AEF（SSS），‎ ‎∴∠EFA＝∠BFA＝∠BFE＝45°，‎ ‎∴∠DFH＝∠EFA＝45°，‎ ‎∴△HDF是等腰直角三角形，‎ ‎∴DH＝DF，HF＝DF，‎ ‎∵∠HDF＝∠CDA＝90°，‎ ‎∴∠HDA＝∠FDC，‎ 在△HDA和△FDC中，‎ ‎，‎ ‎∴△HDA≌△FDC（SAS），‎ ‎∴AF＝CF，‎ ‎∴AH﹣AF＝CF﹣AF＝HF，‎ ‎∴CF﹣AF＝DF，‎ 综上所述，线段AF、CF、DF三者之间的数量关系：AF+CF＝DF或AF﹣CF＝DF或CF﹣AF＝DF，‎ 故答案为：AF+CF＝DF或AF﹣CF＝DF或CF﹣AF＝DF．‎