华师版数学八年级下册同步练习课件-第18章-平行四边形复习与巩固18 16页

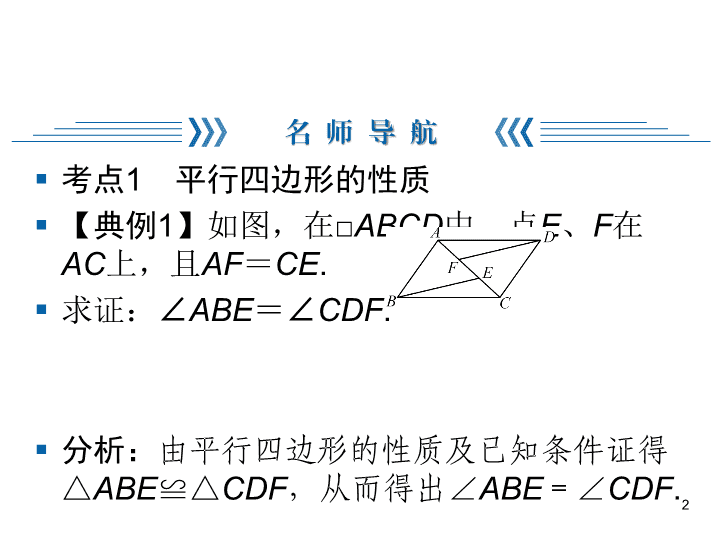
第18章　平行四边形 《平行四边形》复习与巩固 § 考点1　平行四边形的性质 § 【典例1】如图，在□ABCD中，点E、F在 AC上，且AF＝CE. § 求证：∠ABE＝∠CDF. § 分析：由平行四边形的性质及已知条件证得 △ABE≌△CDF，从而得出∠ABE＝∠CDF.2 § 点评：证明两条线段相等或两个角相等，一般是通过证明线段或角所在 的三角形全等来解决，而根据平行四边形的性质可以得出三角形全等的 条件． 3 § 【典例2】已知□ABCD的周长为30 cm，它 的对角线AC和BD交于点O，且△AOB的周 长比△BOC的周长长5 cm，求AB、AD的 长． 4 § 解答：∵△AOB的周长比△BOC的周长长5 cm， § ∴AO＋AB＋BO－(BO＋OC＋BC)＝5 cm. § ∵四边形ABCD是平行四边形， § ∴AD＝BC，AO＝OC， § ∴AB－BC＝5 cm. § ∵□ABCD的周长为30 cm， § ∴AB＋BC＝15 cm， § ∴AB＝10 cm，BC＝5 cm， § ∴AD＝BC＝5 cm. § 点评：平行四边形的两条对角线互相平分，把平行四边形分成两 对全等的三角形，相邻的两个三角形的周长差等于平行四边形邻 边的长度差． 5 § 考点2　平行四边形的判定 § 【典例3】如图，E、F为□ABCD的对角线 AC所在直线上的两点，且AE＝CF.求证：四 边形EBFD是平行四边形． § 分析：(方法一)由四边形ABCD是平行四边形， 可知AB∥CD，AB＝CD，则∠BAC＝ ∠DCA，故∠BAE＝∠DCF.又AE＝CF，从 而可得△BAE≌△DCF，则BE＝DF.同理可 得DE＝BF，即可证得结论；(方法二)从对角 线入手，这两个四边形具有共同的对角线BD， 因此连结BD，证出EF、BD互相平分，亦可 证得结论． 6 § 证明：(方法一)∵四边形ABCD为平行四边形， § ∴AB∥CD，AB＝CD，∴∠BAC＝∠DCA，∴∠BAE＝∠DCF. § 又∵AE＝CF，∴△BAE≌△DCF，∴BE＝DF. § 同理可得DE＝BF. § ∴四边形EBFD是平行四边形． § (方法二)连结BD交AC于点O. § ∵四边形ABCD为平行四边形，∴AO＝CO，BO＝DO. § 又∵AE＝CF，∴AO＋AE＝CO＋CF，即OE＝OF， § ∴四边形EBFD是平行四边形． § 点评：(1)各种判定方法互相关联，认真观察题中的条件，选择恰 当的判定方法．(2)平行四边形的判定经常与性质联系在一起，要 注意它们的区别和联系． 7 § ★考点1　平行四边形的性质 § 1．如图，□ABCD的对角线AC、BD相交于点O，EF过点O与AD、 BC分别相交于点E、F，若AB＝4，BC＝5，OE＝1.5，那么四边 形EFCD的周长为(　　) § A．16 B．14 § C．12 D．10 8 C 　 § 2．如图，在□ABCD中，已知AD＝12 cm，AB＝6 cm，AE平分 ∠BAD交BC于点E，则CE的长等于(　　) § A．8 cm B．6 cm § C．4 cm D．2 cm § 3．如图，□ABCD的对角线AC、BD相交于点O，则下列说法一 定正确的是 § (　　) § A．AO＝OD B．AO⊥OD § C．AO＝OC D．AO⊥AB 9 B 　 C 　 10 6　 6　 § 6．【江苏无锡中考】如图，平行四边形 ABCD中，E、F分别是边BC、AD的中点， 求证：∠ABF＝∠CDE. 11 § ★考点2　平行四边形的判定 § 1．在下列给出的条件中，不能判定四边形ABCD是平行四边形的 是(　　) § A．AB＝CD，AD＝BC B．AB∥CD，AD＝BC § C．AB∥CD，AB＝CD D．AB∥CD，AD∥BC § 2．如图，在△ABC中，AB＝6，AC＝10，点D、E、F分别是AB、 BC、AC的中点，则四边形ADEF的周长为(　　) § A．8 B．10 § C．12 D．16 12 B 　 D 　 § 3．【安徽中考】□ABCD中，E、F是对角 线BD上不同的两点．下列条件中，不能得出 四边形AECF一定为平行四边形的是(　　) § A．BE＝DF B．AE＝CF § C．AF∥CE D．∠BAE＝∠DCF § 解析：如图，连结AC与BD相交于点O.在 □ABCD中，OA＝OC，OB＝OD，要使四 边形AECF为平行四边形，只需证得OE＝OF 即可．若BE＝DF，则OB－BE＝OD－DF， 即OE＝OF，故A不符合题意；若AE＝CF， 则无法判断OE＝OF，故B符合题意；由 AF∥CE能够利用“角边角”证得 △AOF≌△COE，从而得到OE＝OF，故C 不符合题意；由∠BAE＝∠DCF能够利用 “角边角”证得△ABE≌△CDF，从而得到 BE＝DF，然后同A，故D不符合题意．故选 B． 13 B 　 § 4．如图，四边形ABCD的对角线交于点O，从下列条件： ①AD∥BC；②AB＝CD；③AO＝CO；④∠ABC＝∠ADC中， 选出两个可使四边形ABCD是平行四边形，则你选的两个条件是 ____________________.(填写一组序号即可) 14 ①③(答案不唯一)　 § 5．如图，在四边形ABCD中，AD∥BC，延长 BC到点E，使CE＝BC，连结AE交CD于点F，点 F是CD的中点．求证： § (1)△ADF≌ △ECF； § (2)四边形ABCD是平行四边形． 15 § 6．如图，四边形ABCD中，BD垂直平分AC， 垂足为F，E为四边形ABCD外一点，且 ∠ADE＝∠BAD，AE⊥AC. § (1)求证：四边形ABDE是平行四边形； § (2)如果DA平分∠BDE，AB＝5，AD＝6，求 AC的长． 16