人教版八年级上册数学同步练习课件-第13章-13等边三角形 16页

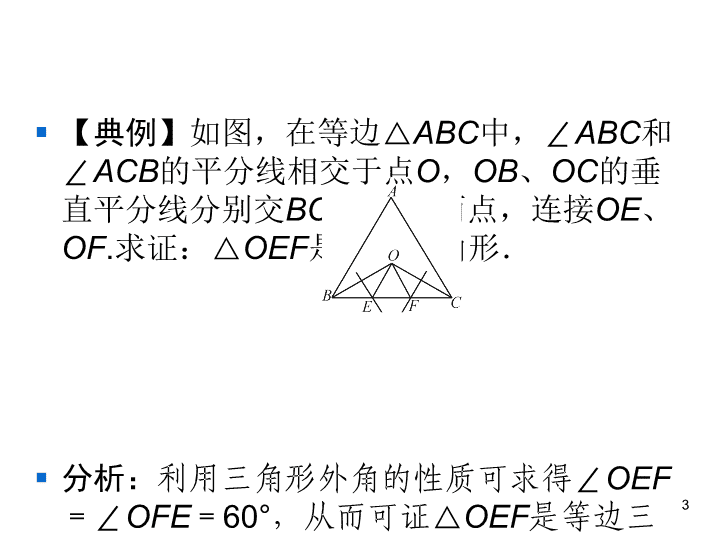
第十三章　轴对称 13.3　等腰三角形 第三课时　等边三角形的性质和判定 13.3.2　等边三角形 § 知识点1　等边三角形的概念 § 三边都相等的三角形是等边三角形． § 知识点2　等边三角形的性质 § (1)等边三角形的三边都相等． § (2)等边三角形的三个内角都相等，并且每一 个角都等于60°. § (3)等边三角形是特殊等腰三角形，它具有等 腰三角形的一切性质． § 知识点3　等边三角形的判定 § (1)三条边都相等的三角形是等边三角形． § (2)三个角都相等的三角形是等边三角形． § (3)有一个角是60°的等腰三角形是等边三角 形． 2 § 【典例】如图，在等边△ABC中，∠ABC和 ∠ACB的平分线相交于点O，OB、OC的垂 直平分线分别交BC于E、F两点，连接OE、 OF.求证：△OEF是等边三角形． § 分析：利用三角形外角的性质可求得∠OEF ＝∠OFE＝60°，从而可证△OEF是等边三 角形． 3 § 证明：∵E、F分别是OB、OC的垂直平分线 上的点， § ∴OE＝BE，OF＝CF， § ∴∠OBE＝∠BOE，∠OCF＝∠COF. § ∵△ABC是等边三角形，且OB、OC分别平 分∠ABC、∠ACB， § ∴∠OBE＝∠BOE＝∠OCF＝∠COF＝30°， § ∴∠OEF＝∠OFE＝60°， § ∴△OEF是等边三角形． 4 § 1．如图，直线l∥m∥n，等边△ABC的顶点B、C分 别在直线n、m上，边BC与直线n所夹锐角为25°， 则∠α的度数为(　　) § A．25°　　 B．45°　　 § C．35°　　 D．30° § 2．【2018·湖南湘潭中考】如图，在等边△ABC中， 点D是边BC的中点，则∠BAD＝___________. 5 C 　 30°　 § 3．如图，AB＝6 cm，AD平分∠BAC，则 △ABC是__________三角形，CD＝ _________cm. § 4．在△ABC中，AD⊥BC，垂足为点D，且 BD＝DC，再补充下面的一个条件：①AB＝ AC；②AB＝BC；③∠B＝60°，其中能使 △ABC是等边三角形的是___________.(填 序号) 6 等边　 3　 ②或③　 § 5．如图，在等边△ABC中，点D、E分别在 边BC、AC上，且DE∥AB，过点E作 EF⊥DE，交BC的延长线于点F. § (1)求∠F的度数； § (2)若CD＝2，求DF的长． § 解：(1)∵△ABC为等边三角形，∴∠B＝ 60°.∵DE∥AB，∴∠EDC＝∠B＝ 60°.∵EF⊥DE，∴∠DEF＝90°，∴∠F ＝90°－∠EDC＝30°.　(2)∵△ABC为等 边三角形，DE∥AB，∴∠EDF＝∠B＝∠A ＝∠DEC＝60°，∴EC＝DC＝2.∵EF⊥DE， ∴∠DEF＝90°，∴∠CEF＝90°－∠DEC ＝30°＝∠F，∴CE＝CF，∴DF＝DC＋CF ＝2CD＝4. 7 § 6．已知：如图，点D在等边 △ABC的边AB上，点F在边AC上， 连接DF并延长交BC的延长线于 点E，FE＝FD. § 求证：AD＝CE. § 证明：过点D作DM∥BE，交AC 于点M，则有∠MDF＝∠E.在 △MDF和△CEF中，∠MFD＝ ∠CFE，FD＝FE, ∠MDF＝∠E， ∴△MDF≌△CEF，∴DM＝ CE.∵△ABC为等边三角形， ∴∠A＝∠B＝∠ACB＝ 60°.∵DM∥BE，∴∠ADM＝ ∠B＝60°，∠AMD＝∠ACB＝ 60°，∴△ADM为等边三角形， ∴DM＝AD，∴AD＝CE. 8 § 7．如图，∠AOB＝120°，OP平分∠AOB， 且OP＝2.若点M、N分别在OA、OB上，且 △PMN为等边三角形，则满足上述条件的 △PMN有(　　) § A．1个　　 B．2个　　 § C．3个　　 D．3个以上 9 D 　 等边三角形　　 § 9．如图，在等边△ABC中，点D、 E分别在边BC、AB上，且BD＝ AE，AD与CE交于点F，则 ∠DFC的度数为___________. § 10．如图，在等边△ABC中，AB ＝8，E是BA延长线上一点，且 EA＝4，D是BC上一点，且ED＝ EC，则BD的长为_________. 10 60°　 4　 § 11．学完“等边三角形”一节后，老师布置 了一道思考题：如图，点M、N分别是等边三 角形ABC的BC、CA边上的点且BM＝CN， AM、BN交于点Q.求证：∠BQM＝60°. 11 (1)请你完成这道思考题； (2)做完(1)后，同学们在老师的启发下进行了反思，提出 了许多问题，如： ①若将题中“BM＝CN”与“∠BQM＝60°”的位置交 换，得到的是否仍是真命题？ ②若将题中的点M、N分别移动到BC、CA的延长线上， 是否仍能得到∠BQM＝60°？ § 请你作出判断，在下列横线上填写“是”或 “否”：①_________；②_________.并对 ①②的判断，选择一个给出证明． § (1)证明：∵△ABC是等边三角形，∴∠ABM ＝∠BCN，AB＝BC.又∵BM＝CN， ∴△ABM≌△BCN，∴∠BAM＝∠CBN， ∴∠BQM＝∠BAM＋∠ABQ＝∠CBN＋ ∠ABQ＝∠ABC＝60°.　(2)②的证明： ∵△ABC是等边三角形，∴∠BAC＝∠ACB ＝60°，AB＝BC＝AC.∵BM＝CN，∴CM ＝AN，∠ACM＝∠BAN＝120°， ∴△ACM≌△BAN，∴∠AMC＝∠BNA， ∴∠NQA＝∠NBC＋∠BMQ＝∠NBC＋ ∠BNA＝180°－60°＝120°，∴∠BQM ＝180°－∠NQA＝60°. 12 是　 是　 § 12．在数学探究课上，老师出示了这样的探 究问题，请你一起探究： § 已知：C为线段AB所在的平面内的任意一点， 分别以AC、BC为边，在AB同侧作等边 △ACE和等边△BCD，连接AD、BE交于点P. § (1)如图1，当点C在线段AB上移动时，线段 AD与BE的数量关系是_____________； 13 AD＝BE　 § (2)如图2，当点C在直线AB外， 且 ∠ACB<120°时，上面的结论是否还成立？ 若成立请证明，不成立说明理由．此时 ∠APE是否随着∠ACB的大小发生变化，若 变化，写出变化规律；若不变，请求出 ∠APE的度数； § (3)如图3，在(2)的条件下，以AB为边在AB 另一侧作等边△ABF，连接AD、BE和CF交 于点P，求证：PB＋PC＋PA＝BE. 14 15 16