华师版数学八年级上册课件-第12章-12乘法公式 13页

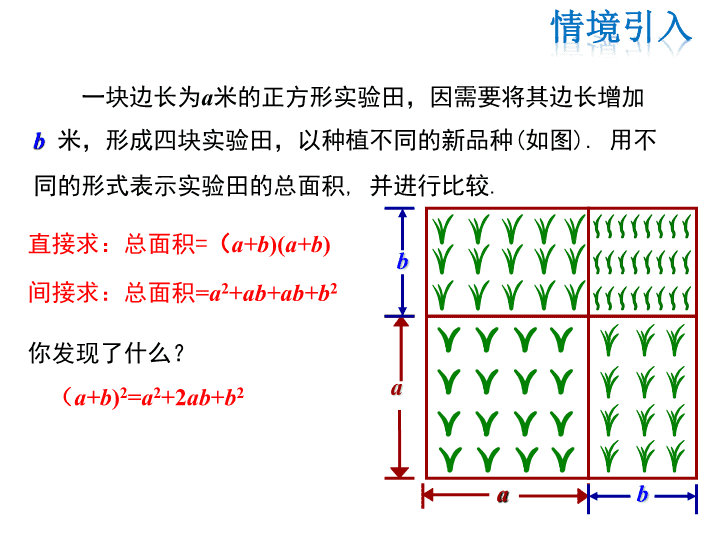
第12章 整式的乘除 12.3 乘法公式 第2课时 两数和（差）的平方 直接求：总面积=（a+b)(a+b) 间接求：总面积=a2+ab+ab+b2 你发现了什么？ （a+b)2=a2+2ab+b2 完全平方公式 计算下列多项式的积，你能发现什么规律？ （1） （p+1)2=(p+1)(p+1)= ；p2+2p+1 （2） （m+2)2=(m+2)(m+2)= ；m2+4m+4 （3） （p-1)2=(p-1)(p-1)= ；p2-2p+1 （4） （m-2)2=(m-2)(m-2)= .m2-4m+4 根据上面的规律，你能直接下面式子的写出答案吗？ （a+b)2= .a2+2ab+b2 （a+b）2= .a2+2ab+b2 这就是说，两数和的平方，等于这两数的平方和加上它 们的积的2倍. 这个公式叫做两数和的平方公式. 简记为：“首平方，尾平方，积的2倍放中间”. 公式特征： 4.公式中的字母a，b可以表示数、单项式或多项式. 1.积为二次三项式； 2.积中两项为两数的平方和； 3.另一项是两数积的2倍； a 2 b2 ab ab a b a+b a + b a b a 2 ab ab b2 (a+b)2 = a2 + 2ab + b 2 (a+b)2 a2 + 2ab + b2= 【试一试】 观察下图，用等式表示下图中图形面积的运算： 【例1】 计算： (1)(2x+3y)2; 2 (2) 2 .2 ba    解：（1）(2x+3y)2 =(2x)2+2•2x•3y+(3y)2 =4x2+12xy+9y2. 2 2 2 2 2 2 2 2 (2 ) 2 2 2 4 2 .4 b ba ba a ba ab                    （2） 【试一试】 推导两数差的平方公式（a-b）2. 2 2 2 2 2 2 ( ) [ ( )] 2 ( ) ( ) 2 a b a b a a b b a ab b             注意a-b=a+(-b)， 也可以利用两数 和的平方公式来 计算. 这样就得到了两数差的平方公式： （a-b)2= .a2-2ab+b2 这就是说，两数差的平方，等于这两数的平方和减 去它们的积的2倍. 【例2 】计算： (1)(3x-2y)3; 21(2) 1 .2 m     解：（1）(3x-2y)2=(3x)2-2•3x•2y+(2y)2=9x2-12xy+4y2. 2 2 2 2 2 2 2 2 2 1 1 1 11 1.2 2 2 4 1 1 1 1 11 = - 1 2 1 1 .2 2 2 2 4 - 2 1 1 - m m m m m m m m m m m                                                   解法1 解法2 1 （2） 【思考】 (a+b)2与(-a-b)2相等吗? (a-b)2与(b-a)2相等吗? (a-b)2与a2-b2相等吗? 为什么? (a+b)2与(-a-b)2相等.理由如下： (-a-b)2=(-a)2-2·(-a) ·b+b2=a2+2ab+b2=(a+b)2. (a-b)2与(b-a)2相等.理由如下： (b-a)2=b2-2ba+a2=a2-2ab+b2=(a-b)2. (a-b)2与a2-b2不一定相等.只有当b=0或a=b时，(a-b)2=a2-b2. (1) 1022； 解： 1022 = (100+2)2 =10 000+400+4 =10 404. (2) 992. 992 = (100 –1)2 =10 000 -200+1 =9801. 1.运用完全平方公式计算： 解题技巧：利用完全平方公式计算时，先根据式子的特点 选择公式，再准确代入公式，最后进行化简. 2. 运用乘法公式计算: (1) (x+2y-3)(x-2y+3) ; (2) (a+b+c)2. 原式=[x+(2y–3)][x-(2y-3)] = x2-(2y-3)2 = x2-(4y2-12y+9) = x2-4y2+12y-9. 解:(1) (2)原式= [(a+b)+c]2 = (a+b)2+2(a+b)c+c2 = a2+2ab+b2+2ac+2bc+c2 = a2+b2+c2+2ab+2bc+2ac. 解题技巧：第(1)题选用平方差公式进行计算，需要分组， 分组方法是“符号相同的为一组，符号相反的为另一组”. 第(2)题要把其中两项看成一个整体，再按照完全平方公式 进行计算. 3.若a+b=5，ab=-6，求a2+b2，a2-ab+b2. 4.已知x+y=8，x-y=4，求xy. 解：∵a+b=5，ab=-6， ∴a2+b2=（a+b)2-2ab=52-2×(-6)=37； 解：∵x+y=8，∴(x+y)2=64，即x2+y2+2xy=64①. ∵x-y=4， ∴(x-y)2=16，即x2+y2-2xy=16②. ①-②，得4xy=48， ∴xy=12. a2-ab+b2=a2+b2-ab=37-(-6)=43. 完全平方 公 式 法 则 注 意 (a±b)2= a2±2ab+b2 1.项数、符号、字母及其指数 2.不能直接应用公式进行计算的 式子，可能需要先添括号变形成 符合公式要求的 常 用 结 论 3.明确完全平方公式和平方差公 式的区别（从公式结构特点及结 果两方面区分） a2+b2=(a+b)2-2ab=(a-b)2+2ab; 4ab=(a+b)2-(a-b)2