华师版数学八年级上册同步练习课件-第13章-专项训练4解决与等腰三角形有关的问题 20页

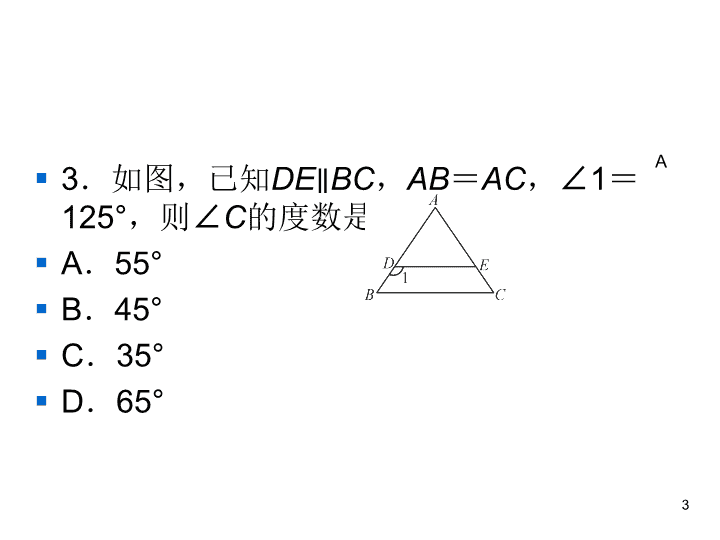
第13章　全等三角形 专项训练四　解决与等腰三角形有关的问题 § 类型1　利用等腰(或等边)三角形的性质求边角 § 1．等腰三角形的两边长分别为3和6，则这个等腰三角形的周长为 (　　) § A．12 B．15 § C．12或15 D．18 § 2．已知等边△ABC的中线BD、CE相交于点O，∠BOC等于 (　　) § A．60° B．150° § C．30° D．120° 2 重难突破 B　 D　 § 3．如图，已知DE∥BC，AB＝AC，∠1＝ 125°，则∠C的度数是(　　) § A．55° § B．45° § C．35° § D．65° 3 A　 § 4．如图，等边三角形ABC与互相平行的直 线a，b相交，若∠1＝25°，则∠2的大小为 (　　) § A．25° § B．35° § C．45° § D．55° 4 B　 § 5．【2018·四川成都中考】等腰三角形的一 个底角为50°，则它的顶角的度数为 ________. § 6．如图，已知△ABC是等腰三角形，D是 BC边的中点，则∠1＋∠C＝______度． 5 80°　 90　 § 7．如图，在等腰三角形纸片ABC中，AB＝ AC，∠A＝50°，折叠该纸片，使点A落在 点B处，折痕为DE，则∠CBE＝________. 6 15°　 § 8．如图，已知AB＝AC＝AD，且AD∥BC. 求证：∠C＝2∠D. § 证明：∵AB＝AC＝AD， § ∴∠C＝∠ABC，∠D＝∠ABD，∴∠ABC ＝∠CBD＋∠D.∵AD∥BC，∴∠CBD＝ ∠D，∴∠ABC＝2∠D.又∵∠C＝∠ABC， ∴∠C＝2∠D. 7 § 类型2　等腰(或等边)三角形的判定 § 9．如图，在△ABC中，∠ABC和∠ACB的 平分线交于点E，过点E作MN∥BC交AB于 点M，交AC于点N，若MN＝9，则BM＋CN 的长为 (　　) § A．6 B．7 § C．8 D．9 8 D　 § 10．【湖北武汉中考】如图，在Rt△ABC中， ∠C＝90°，以△ABC的一边为边画等腰三 角形，使得它的第三个顶点在△ABC的其他 边上，则可以画出的不同的等腰三角形的个 数最多为 (　　) § A．4 § B．5 § C．6 § D．7 9 D　 § 11．如图，AB＝AC，DB＝DC，若∠ABC 为60°，BE＝3 cm，则AB＝_____ cm. 10 6　 § 12．如图，已知△ABC，∠ACB的平分线CD交AB于点D，DE∥BC交 AC于点E.如果EC＝2AE，AC＝5，则DE＝______. 11 § 13．如图，在Rt△ABC中，在斜边 AB和直角边AC上分别取一点D、E， 使DE＝DA，延长DE交BC的延长 线于点F.△DFB是等腰三角形吗？ 请说明你的理由． § 解：△DFB是等腰三角形．理由如 下：∵DE＝DA，∴∠A＝ ∠AED.∵∠AED＝∠CEF，∴∠A ＝∠CEF.∵∠ACB＝∠ECF＝ 90°，∴∠A＋∠B＝∠CEF＋∠F， ∴∠B＝∠F，∴DB＝DF， ∴△DFB是等腰三角形． 12 § 14．如图，在等边△ABC中，点D、E分别在 边BC、AC上，且DE∥AB，过点E作EF⊥DE， 交BC的延长线于点F. § (1)求∠F的度数； § (2)若CD＝3，求DF的长． 13 解：(1)∵△ABC是等边三角形，∴∠B＝60°.∵DE∥AB，∴∠EDC＝∠B＝ 60°.∵EF⊥DE，∴∠DEF＝90°，∴∠F＝90°－∠EDC＝30°.　(2)∵∠ACB＝ 60°，∠EDC＝60°，∴△EDC是等边三角形，∴CE＝DC＝3.∵∠ACB＝60°， ∠F＝30°，∴∠CEF＝∠F＝30°，∴CF＝CE＝3，∴DF＝DC＋CF＝6. § 类型3　等腰(或等边)三角形在实际生活中的 应用 § 15．同学们都玩过跷跷板，如图是一跷跷板 的示意图，立柱OC与地面垂直，OA＝OB， 当跷跷板的一头A着地时，∠OAC＝25°， 则当跷跷板的另一头B着地时，∠AOA′等 于 (　　) § A．25° B．50° § C．60° D．130° 14 B　 § 16．如图，上午8时，一艘轮船从A处出发以 每小时20海里的速度向正北航行，10时到达 B处，轮船在A处测得灯塔C在北偏西36°， 航行到B处时，又测得灯塔C在北偏西72°， 则从B到灯塔C的距离是__________. 15 40海里　 16 17 § 18．已知，在△ABC中，点D在BC上，点E 在BC的延长线上，且BD＝BA，CE＝CA. § (1)如图1，若∠BAC＝90°，∠B＝45°， 试求∠DAE的度数； § (2)若∠BAC＝90°，∠B＝60°，求∠DAE 的度数； § (3)如图2，若∠BAC＞90°，其余条件不变， 探究∠DAE与∠BAC之间有怎样的数量关系？ 18 图1 图2 19 20