人教版八年级上册数学同步练习课件-第11章-三角形 复习与巩固11 16页

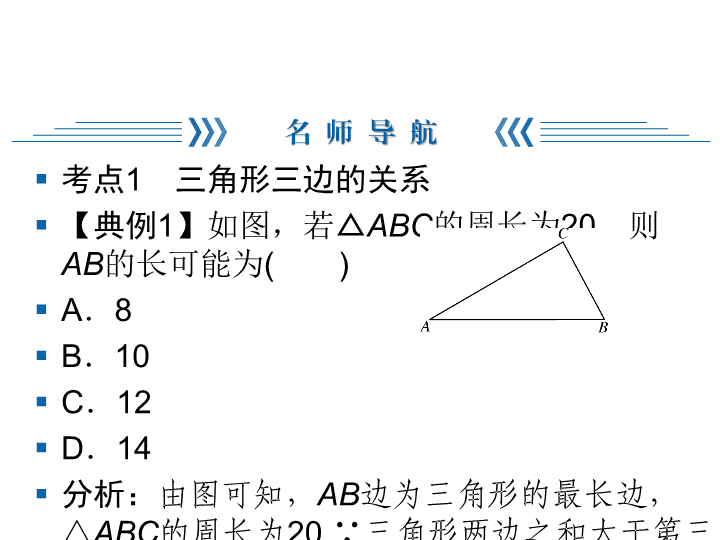
《三角形》复习与巩固 § 考点1　三角形三边的关系 § 【典例1】如图，若△ABC的周长为20，则 AB的长可能为(　　) § A．8　　 § B．10 § C．12　　 § D．14 § 分析：由图可知，AB边为三角形的最长边， △ABC的周长为20.∵三角形两边之和大于第 三边，∴AB的长小于10. § 答案：A 2 § 考点2　与三角形有关的角的计算 § 【典例2】如图，△ABC中，∠A＝30°， ∠B＝62°，CE平分∠ACB，CD⊥AB于点 D，DF⊥CE于点F，求∠CDF的度数． § 分析：若想求∠CDF的度数，则可求∠CDF 的余角∠FCD，∠FCD＝∠FCB－∠DCB.又 ∠FCB是∠ACB的一半，∠ACB可利用 △ABC的内角和定理求出；∠DCB可通过 ∠B的余角求出．这样就可求出∠CDF的度 数． 3 4 § 考点3　三角形外角性质的应用 § 【典例3】如图，已知D是△ABC边BC延长 线上一点，DF⊥AB于点F，交AC于点E， ∠A＝35°，∠D＝42°.求： § (1)∠ACD的度数； § (2)∠AEF的度数． § 分析：(1)若想求∠ACD的度数，则可由 ∠ACD是△ABC的外角求得，即∠ACD＝ ∠B＋∠A，其中∠B通过是∠D的余角求得； (2)若想求∠AEF的度数，可由△AEF的内角 和求得． 5 § 解答：(1)∵DF⊥AB，∴∠B＝90°－∠D＝ 48°. § ∵∠ACD是△ABC的一个外角，∴∠ACD＝ ∠A＋∠B＝83°. § (2)∵DF⊥AB，∴∠AFD＝90°，∴∠AEF ＝90°－∠A＝55°. 6 § 考点4　多边形内、外角和的应用 § 【典例4】正多边形的一个内角的度数恰好等 于它的相邻外角的度数的3倍，则这个正多边 形的边数为________． § 分析：设正多边形的一个外角等于x°. § ∵正多边形一个内角的度数恰好等于它的外 角的度数的3倍， § ∴这个正多边形的一个内角为3x°， § ∴x＋3x＝180，解得x＝45. § ∴这个多边形的边数是360°÷45°＝8. § 答案：8 7 § ★考点1　三角形三边的关系 § 1．一个等腰三角形一边长为4 cm，另一边 长为5 cm，那么这个等腰三角形的周长是(　 　) § A．13 cm　　 B．14 cm § C．13 cm或14 cm　　 D．以上都不对 8 C 　 § 2．已知三角形三边长分别为2，x,13，若x为 正整数，则这样的三角形个数为 § (　　) § A．2　　 B．3　　 § C．5　　 D．13 § 解析：∵11＜x＜15，且x为整数，则x＝ 12,13,14，∴有3个三角形． § 3．已知三角形三边长分别为a、b、c，其中 a、b满足(a－6)2＋|b－8|＝0，求这个三角形 最长边c的取值范围． § 解：∵(a－6)2＋|b－8|＝0，∴a－6＝0，b－ 8＝0，∴a＝6，b＝8.∵这个三角形的最长 边为c，∴b