等腰三角形的轴对称性教案（2） 3页

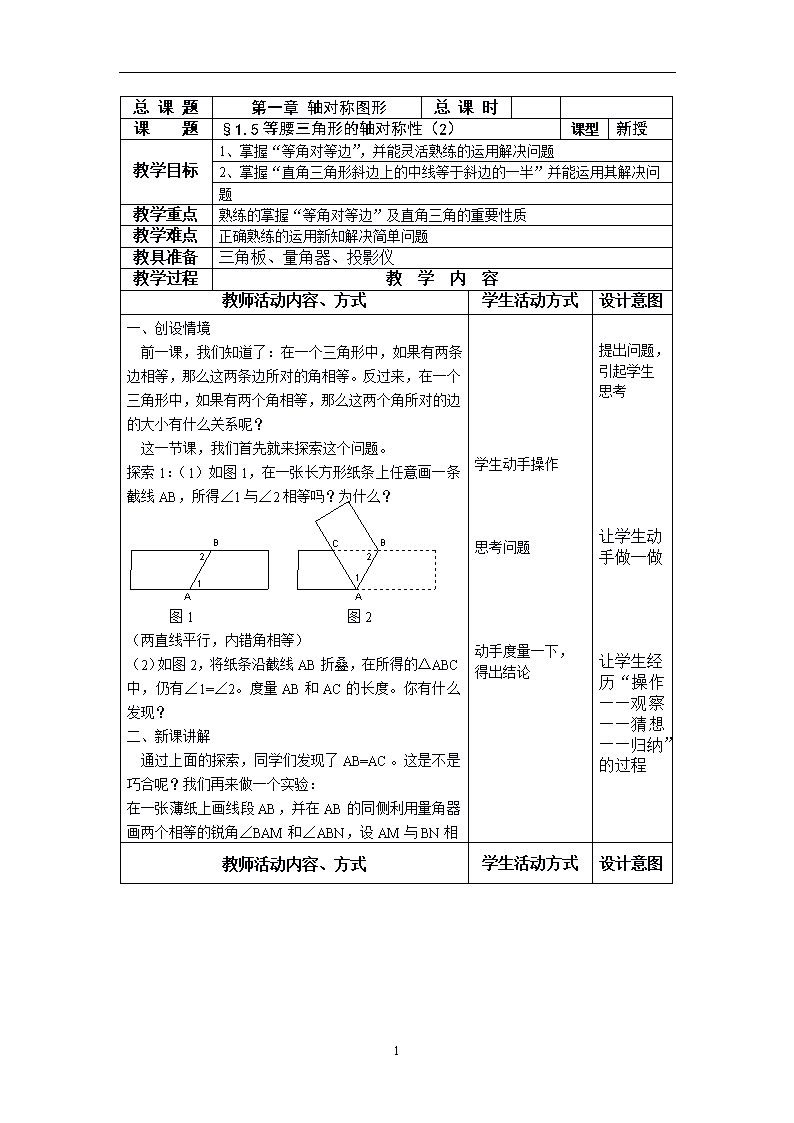
‎ ‎ 总 课 题 第一章 轴对称图形 总 课 时 课 题 ‎§1.5等腰三角形的轴对称性（2）‎ 课型 新授 教学目标 ‎1、掌握“等角对等边”，并能灵活熟练的运用解决问题 ‎2、掌握“直角三角形斜边上的中线等于斜边的一半”并能运用其解决问 题 教学重点 熟练的掌握“等角对等边”及直角三角的重要性质 教学难点 正确熟练的运用新知解决简单问题 教具准备 三角板、量角器、投影仪 教学过程 教 学 内 容 教师活动内容、方式 学生活动方式 设计意图 一、创设情境 ‎ 前一课，我们知道了：在一个三角形中，如果有两条边相等，那么这两条边所对的角相等。反过来，在一个三角形中，如果有两个角相等，那么这两个角所对的边的大小有什么关系呢？‎ ‎ 这一节课，我们首先就来探索这个问题。‎ 探索1：（1）如图1，在一张长方形纸条上任意画一条截线AB，所得∠1与∠2相等吗？为什么？‎ ‎ 图1 图2‎ ‎（两直线平行，内错角相等）‎ ‎（2）如图2，将纸条沿截线AB折叠，在所得的△ABC中，仍有∠1=∠2。度量AB和AC的长度。你有什么发现？‎ 二、新课讲解 ‎ 通过上面的探索，同学们发现了AB=AC。这是不是巧合呢？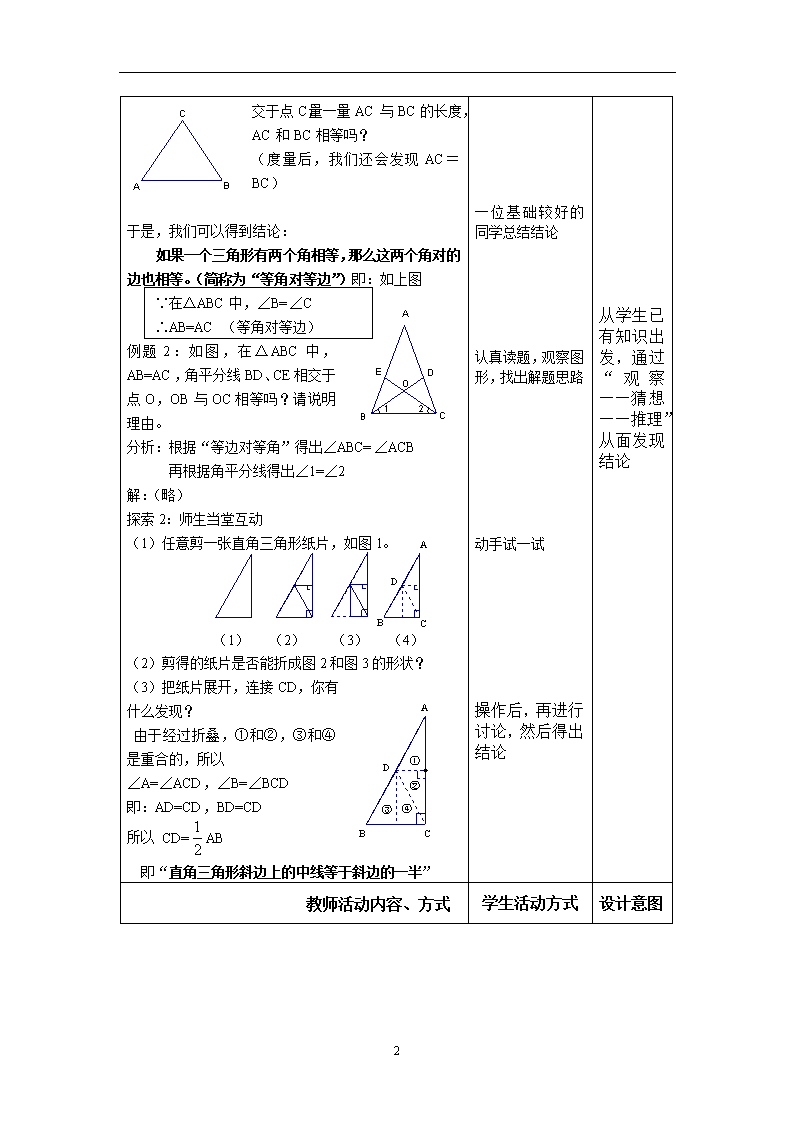我们再来做一个实验：‎ 在一张薄纸上画线段AB，并在AB的同侧利用量角器画两个相等的锐角∠BAM和∠ABN，设AM与BN相 学生动手操作 思考问题 动手度量一下，‎ 得出结论 提出问题，‎ 引起学生 思考 让学生动 手做一做 让学生经 历“操作——观察——猜想——归纳”的过程 教师活动内容、方式 学生活动方式 设计意图 3‎ ‎ ‎ 交于点C，量一量AC与BC的长度，AC和BC相等吗？‎ ‎（度量后，我们还会发现AC＝BC）‎ 于是，我们可以得到结论：‎ 如果一个三角形有两个角相等，那么这两个角对的边也相等。（简称为“等角对等边”）即：如上图 ‎∵在△ABC中，∠B=∠C ‎∴AB=AC （等角对等边）‎ 例题2：如图，在△ABC中，AB=AC，角平分线BD、CE相交于点O，OB与OC相等吗？请说明理由。‎ 分析：根据“等边对等角”得出∠ABC=∠ACB ‎ 再根据角平分线得出∠1=∠2‎ 解：（略）‎ 探索2：师生当堂互动 ‎（1）任意剪一张直角三角形纸片，如图1。‎ ‎（1） （2） （3） （4）‎ ‎（2）剪得的纸片是否能折成图2和图3的形状？‎ ‎（3）把纸片展开，连接CD，你有什么发现？‎ ‎ 由于经过折叠，①和②，③和④是重合的，所以 ‎∠A=∠ACD，∠B=∠BCD 即：AD=CD，BD=CD 所以 CD=AB ‎ 即“直角三角形斜边上的中线等于斜边的一半”‎ 一位基础较好的同学总结结论 认真读题，观察图形，找出解题思路 动手试一试 操作后，再进行讨论，然后得出结论 从学生已有知识出发，通过“观察——猜想——推理”从面发现结论 ‎　　　　　　　　　教师活动内容、方式 学生活动方式 设计意图 3‎ ‎ ‎ 补例：1. 如图，在△ABC中，∠ACB = 90°，CD是AB边上的中线且CD = 5cm，则AB= 。‎ 三、课堂练习 P26练习T1、2、3‎ 四、课堂小结：‎ 探究得到了一判定一个三角形是等腰三角形的条件以及“直角三角形斜边上的中线等于斜边的一半”这个性质，在应用这些结论解决问题的过程中进一步提高了说理、分析、识图和归纳的能力。‎ 课后作业：补充 学生口答，并说明理由 巩固新知识并学会应用 ‎　　　　　　　　　　　　　‎ 3‎