人教版八年级数学上册期中测试题及答案【精品10套】，高分必备 78页

人教版八年级数学上册 期中测试题及答案【精品 10 套】，高分必备 初二数学第一学期期中试卷 （考试时间：100 分钟 满分：100 分） 一．选择题（本大题共 10 小题，每题 3 分，共 30 分.） 1．下列美丽的图案中是轴对称图形的个数有……………………………………（ ） A. 1 个 B. 2 个 C. 3 个 D. 4 个 2．一个等腰三角形的两边长分别是 3 和 7，则它的周长是……………………（ ） A.17 B.15 C. 13 D. 13 或 17 3．下列说法正确的是………………………………………………………………（ ） A. 全等三角形是指形状相同的两个三角形 B. 全等三角形是指面积相等的两个三角形 C. 两个等边三角形是全等三角形 D. 全等三角形是指两个能完全重合的三角形 4. 如图，在边长为 1 个单位长度的小正方形组成的网格中， A、B 都是格点，则线段 AB 的长度为…………………………………………（ ） A. 5 B. 6 C.7 D. 25 5．已知△ABC 中，a、b、c 分别是∠A、∠B、∠C 的对边，下列条件不能判断△ABC 是直角 三角形的是…………………………………………………………………（ ） A. ∠A＝∠C－∠B B. a:b:c＝2:3:4 C. a2＝b2－c2 D.a＝3 4 ，b＝5 4 ，c＝1 6．如图，在△ABC 中，AB＝AC，∠A＝36º，BD、CE 分别是∠ABC、∠BCD 的角平分线，则 图中的等腰三角形有……………………………………………………（ ） A. 5 个 B. 4 个 C. 3 个 D. 2 个 7．如图，四边形 ABC D 关于直线l 是对称的，有下面的结论：①AB∥CD；②AC⊥BD；③AO ＝CO；④AB⊥BC，其中正确的结论有……………………………………（ ） A．①② B．②③ C．①④ D．② 8．如图，将三角形纸片 ABC 折叠，使点 C 与点 A 重合，折痕为 DE. 若∠B＝82º， ∠BAE＝26º，则∠EAD 的度数为………………………………………………（ ） A.28º B. 30º C.36º D.45º 9．如图，∠AOB 的平分线上一点 P 到 OA 的距离为 5，Q 是 OB 上任意一点，则（ ） A．PQ≥5 B．PQ＞5 C．PQ≤5 D．PQ＜5 10．如图，已知∠AOB＝60º，点 P 在边 OA 上，OP＝12，点 M，N 在边 OB 上，PM＝PN， 若 MN＝2，则 OM 的长为……………………………………………………（ ） （第 4 题图） C （第 6 题图） （第 7 题图） l D A B O C P B Q O A （第 9 题图） （第 10 题图） A BO M N 60º （第 8 题图） B A E D （第 19 题图） A B C D EO A B D C （第 16 题图） C AB E D （第 17 题图） O A E B CD P （第 20 题图） A B D C （第 18 题图） A.3 B.4 C.5 D. 6 二．填空题（本大题共 10 小题，每空 2 分，共 20 分.） 11．正方形是一个轴对称图形，它有 条对称轴. 12．等腰三角形的顶角是 80°，一腰上的高与底边的夹角是 °． 13．某直角三角形三条边的平方和为 98，则这个直角三角形的斜边长为 ． 14．直角三角形的一直角边长 6cm，斜边长 10cm，则其斜边上的高是 cm. 15．在△ABC 中，∠A＝80°，当∠B＝ °时，△ABC 是等腰三角形. 16．如图，已知 AD 是线段 BC 的垂直平分线，且 BD＝3cm，△ABC 的周长为 20cm，则 AC ＝ ． 17．如图，△OAD≌△OBC，且∠O＝70°，∠AEB＝100°，则∠C＝ °． 18. 如图，四边形 ABCD 中，BC＝AC＝DC，BC⊥CD，且∠B＝60°，则∠BAD 的度数是 ． 19. 如图，已知 OB、OC 为△ABC 的角平分线，过点 O 作 DE∥BC 交 AB、AC 于 D、E，若 AB ＝7，AC＝5，则△ADE 的周长为 ． 20. 如图，E 为正方形 ABCD 边 AB 上一点，BE＝3AE＝3，P 为对角线 BD 上一个动点，则 PA ＋PE 的最小值是 . 三．解答题（本大题共 6 小题，共 50 分. 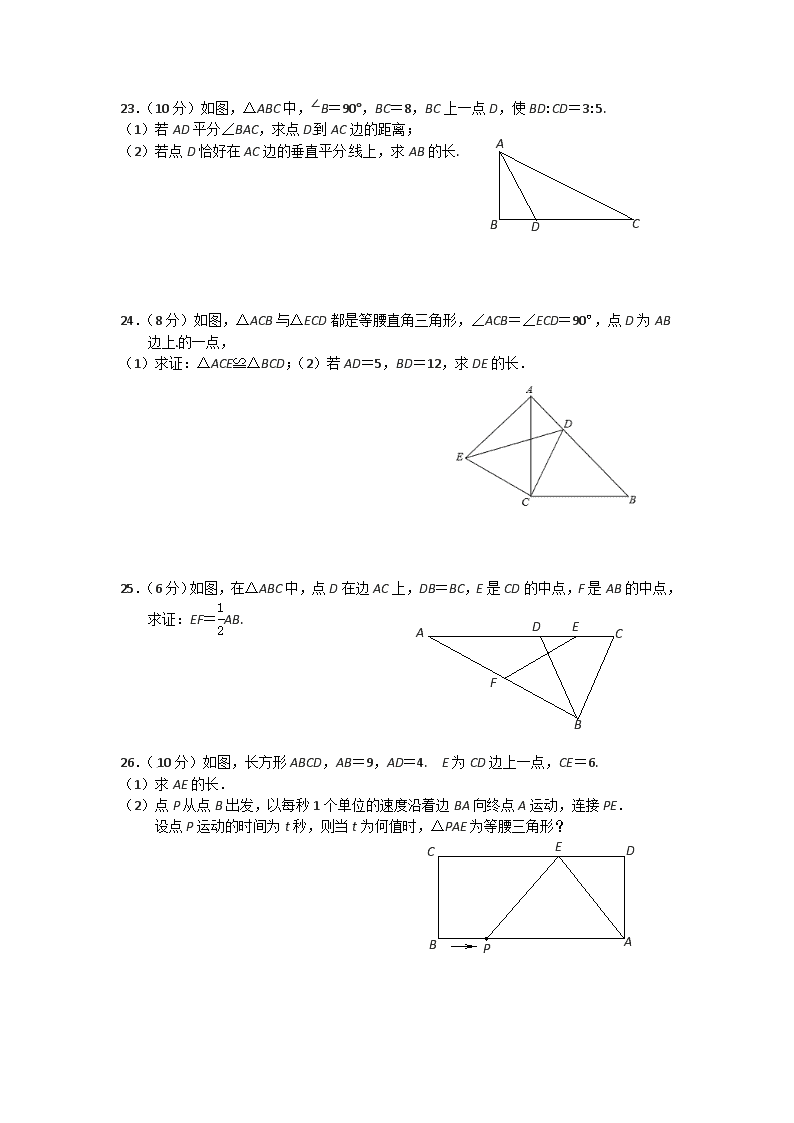解答需写出必要的文字说明或演算步骤） 21．（8 分） （2）如图，在边长为 1 个单位长度的小正方形组成的网格中，按要求作图． ①利用尺规作图在 AC 边上找一点 D，使点 D 到 AB、 BC 的距离相等．（不写作法，保留作图痕迹）； ②在网格中，△ABC 的下方，直接画出△EBC， 使△EBC 与△ABC 全等． 22．（8 分）已知：如图，AB＝AC，∠DAM＝∠DNE＝∠BAC， 求证：△ABD≌△ACE． （1）如图，已知△ABC（AC＜BC），用尺规 在 BC 上确定一点 P，使 PA＋PC＝BC． （不写作法，保留作图痕迹.） B C A A E M C D BN 23．（10 分）如图，△ABC 中，∠B＝90°，BC＝8，BC 上一点 D，使 BD:CD＝3:5. （1）若 AD 平分∠BAC，求点 D 到 AC 边的距离； （2）若点 D 恰好在 AC 边的垂直平分线上，求 AB 的长. 24．（8 分）如图，△ACB 与△ECD 都是等腰直角三角形，∠ACB＝∠ECD＝90º，点 D 为 AB 边上的一点， （1）求证：△ACE≌△BCD；（2）若 AD＝5，BD＝12，求 DE 的长． 25．（6 分）如图，在△ABC 中，点 D 在边 AC 上，DB＝BC，E 是 CD 的中点，F 是 AB 的中点， 求证：EF＝1 2 AB. 26．（10 分）如图，长方形 ABCD，AB＝9，AD＝4. E 为 CD 边上一点，CE＝6. （1）求 AE 的长． （2）点 P 从点 B 出发，以每秒 1 个单位的速度沿着边 BA 向终点 A 运动，连接 PE． 设点 P 运动的时间为 t 秒，则当 t 为何值时，△PAE 为等腰三角形？ P AB E DC A B CD A B CD E F 初二数学期中考试参考答案与评分标准 一、选择题（每题 3 分）C A D A B A D C A C 二、填空题（每空 2 分） 11. 4 12. 40º 13. 7 14. 4.8 15. 80º或 50 º或 20º 16. 7cm 17.15 18. 135 º 19. 12 20. 5 三、解答题 21.（1）作 AB 的垂直平分线，与 BC 的交点即为点 P………………………………（3 分） （2）①作∠ABC 的角平分线，与 AC 的交点即为点 D…………………………（6 分） ②符合条件的点 E 有两个……………………………………………………（8 分） 22. 先证∠DAB＝∠EAC…………………………………………………………………（2 分） 再证∠D＝∠E………………………………………………………………………（5 分）又∵AB＝AC，∴△ABD ≌△ACE．………………………………………………（8 分） 23. ∵BC＝8，且 BD:CD＝3:5，∴BD＝3，CD＝5…………………………………（2 分） （1）作 DH⊥AC 于 H………………………………………………………………（3 分） 又∵AD 平分∠BAC，∠B＝90°，∴DH＝BD＝3…………………………（5 分） 即点 D 到 AC 边的距离是 3…………………………………………………（6 分） （2）∵点 D 恰好在 AC 边的垂直平分线上，∴AD＝CD＝5……………………（8 分） 在 Rt△ABD 中，AD＝5，BD＝3，∴AB＝4………………………………（10 分） 24.（1）先证∠ECA＝∠DCB……………………………………………………………（2 分） 又有 EC＝DC，AC＝BC………………………………………………………（3 分） ∴△ACE≌△BCD………………………………………………………………（4 分） （2）∴AE＝BD＝12，∠EAC＝∠B＝45°……………………………………………（6 分） ∴∠EAD＝∠EAC＋∠CAD＝90°………………………………………………（7 分） 在 Rt△ADE 中，AD＝5，AE＝12，∴DE＝13………………………………（8 分） 25. 证明：连结 BE（图略）……………………………………………………………（1 分） ∵在△BCD 中，DB＝BC，E 是 CD 的中点，∴BE⊥CD……………………（4 分） 在 Rt△ABE 中，EF 是斜边 AB 上的中线，∴EF＝1 2 AB………………………（6 分） 26. （1）在长方形 ABCD 中，∠D＝90°，CD＝AB＝9………………………………（1 分） 在 Rt△ADE 中，DE＝9－6＝3，AD＝4，∴AE＝5………………………（3 分） （2）若△PAE 为等腰三角形，则有三种可能. 当 EP＝EA 时，AP＝6，∴t＝BP＝3………………………………………………（5 分）当 AP＝AE 时， 则 9－t＝5，∴t＝4………………………………………………（7 分） 当 PE＝PA 时，则(6－t)2＋42＝(9－t)2，∴t＝29 6 …………………………………（10 分）综上所述， 符合要求的 t 值为 3 或 4 或29 6 . 八年级数学上册期中测试题及答案 ( 考试时间 100 分钟 满分 120 分 ) 一、精心选一选，把唯一正确的答案填入题前括号内！(每小题 2 分，共 26 分) 1、（ ）4 平方根是 A、2 B、±2 C、 2 D、± 2 2、（ ）下列写法错误的是 A、 2.004.0  B、 1.001.0  C、 981  D、 3 64 ＝－４ 3、（ ）计算 25 － 3 8 的结果是 A、3 B、7 C、－3 D、7 4、（ ）分解因式 x3－x 的结果是 A、x（x2－1） B、x（x－1）2 C、x（x＋1）2 D、x（x＋1）（x－1） 5、（ ）计算 x 32 x 的结果是 A、x 6 B、 2x C、 3x D、 5x 6、（ ）和数轴上的点一一对应的数是 A、分数 B、有理数 C、无理数 D、实数 7、（ ）在实数 4 ，0， 7 22 ， 3 125.0 ，0.1010010001…， 3 ， 2  中无理数有 A、0 个 B、1 个 C、2 个 D、3 个 8、（ ）我们知道 5 是一个无理数，那么 5 － 1 在哪两个整数之间? A、1 与 2 B、2 与 3 C、3 与 4 D、4 与 5 9、（ ）（2 + x）（x－2）的结果是 A、2 － x2 B、2+x2 C、4 + x2 D、x2－4 10、（ ）如果   nxmx  中不含 x 的项，则 m、n 满足 0.,.,0.,.  nDnmCmBnmA 11、（ ）计算 2 ( 1)( 1)a a a   的结果为 A、1 B、 1 C、 22 1a  D、 22 1a  12、（ ）如图 1 所示：求黑色部分（长方形）的面积为 A、24 B、30 C、48 D、18 13、（ ）设三角形的三边分别是下列各组数，则不是直角三角形的一组是 图 1 A、3，4，5； B、6，8，10； C、5，12,13； D、5，6，8； 二、认真填一填，把答案写在横线上，相信你能填对！(每小题 2 分，共 26 分） 14、计算： 2( 9 3 ) ( 3 )x x x     ____ . 15、若 a、b、c 是△ABC 的三边，且 a = 3cm，b = 4 cm,ｃ＝５cm ,则△ABC 最大边上的高是 __________ 16、多项式 2 26 3a b a b 的公因式是 . 17、若（x－1）（x＋1）= x2 ＋px－1，则 p 的值是______. 18、如图 2，有两棵树，一棵高 6 米，另一棵高 2 米，两树相距 3 米， 一只小鸟 从 一棵树的树梢飞到另一棵树的树梢，至少飞了 米. 19、计算（1 + x）（x－１）（x 2 ＋1）的结果是 . 20、用简便方法计算 2008 2 －4016×2007+2007 2 的结果是 ____ _. 21、已知 x2＋x－1 = 0，则代数式 x3＋2x2 ＋2008 的值为 . 22、如图 3，一棵大树在一次强台风中于离地面 3 米处折断 倒下，倒下后的树顶与树根的距离为 4 米，这棵大树在折断 前的高度为________ 米 。 23、若一个正数的两个平方根是 2 1a  和ａ－２，这个正数是 图 3 24、在横线处填上适当的数，使等式成立： 2 2 4 1______2 1       xxx 25、如图 4,为了测量一湖泊的宽度,小明在点 A,B,C 分别设桩,使 BCAB  , 并量得 AC = 52 m ,BC = 48 m ,请你算出湖泊的宽度应为_________米。 26、 已知： ，则m m m m    1 3 12 2 _____________ . 图 4 三、细心计算、化简、或求解，解答应写出必要的计算过程，写好步骤，按步给分。 注意：(27 题 6 分；28 题至 33 题, 每小题 3 分，计 18 分；34 小题 4 分；35 题至 38 题, 每 小题 5 分，计 20 分，共 48 分） 27、因式分解： ① mm 93  ② x2（x－y）－（x－y） ④ 3a 2 － 6a + 3 30° 图 2 28、计算：  2 33 8 4   29、计算：x3.(2x3)2÷  24x 30、化简(x2－ x) 3 +( 3x4－ 2x3 )÷( － x 2 ) 31、计算：       23 1 2 16 2 aaa 32、计算：(x－1)(x－3)－(x－1)2 33、解方程： 04)2( 2 x 34、先化简再求值：    22 2 2a b a b a b    －  22ba ，其中 3,3 1  ba . 35、如图已知，每个小方格是边长为 1 的正方形，求△ABC 的周长 (结果用根号表示)。 36、已知某开发区有一块四边形的空地 ABCD，如图，现计划在该空地上种上草皮，经测量 ∠A＝60°，AB＝AD＝8m，CD＝10m，BC＝6m，若每平方米草皮需要 200 元，问需要投入多 少资金？（ 3 ≈1.73） D C B A 37、如图，在笔直的某公路上有 A、B 两点相距 50km，C、D 为两村庄，DA⊥AB 于点 A，CB⊥AB 于点 B，已知 DA=30km，CB=20km，现在要在公路的 AB 段上建一个土特产品收购站 E， 使得 C、D 两村到收购站 E 的距离相等，则收购站 E 应建在离 A 点多远处？ 38、 如图，居民楼与马路是平行的，相距 9m，在距离载重汽车 41m 处就可受到噪声影响， 试求在马路上以 4m/s 速度行驶的载重汽车，给一楼的居民带来多长时间的噪音影响？ 若时间超过 25 秒，则此路禁止该车通行，你认为载重汽车可以在这条路上通行吗？(本 题 6 分) 马路 A 居民区 汽车 B 马路 附加题：(每小题 10 分,共 20 分) 1、已知，如图，四边形 ABCD中， 1AB BC  ， 3C D  ， 1D A  ，且 090B  。 试求：（1） B A D 的度数； （2）四边形 ABCD 的面积（结果保留根号）。 第 38 题 A D E B C A B C D 2、有一天张老师在黑板上写出三个算式： 5 2 一 3 2 = 8×2， 9 2 －7 2 = 8×4，15 2 －3 2 = 8×27， 王华接着又写了两个具有同样规律的算式：11 2 5 2 = 8×12，15 2 －7 2 = 8×22，…… (1)请你再写出两个（不同于上面算式）具有上述规律的算式； (2)用文字写出反映上述算式的规律； (3 )试说明这个规律的是正确的。 参考答案 一、 精心选一选，把唯一正确的答案填入括号内！(每题 2 分，共 28 分) 二、认真填一填，把答案写在横线上，相信你能填对！(每小题 2 分，共 20 分） 三、细心计算、化简、或求解，解答应写出必要的计算过程，写好步骤，按步给分。 注意：(27 题 6 分；28 题至 33 题, 每小题 3 分，计 18 分；34 小题 4 分；35 题至 38 题, 每小题 5 分，计 20 分，共 48 分） 27、①m )3)(3(  mm ②（x－y）（x+1）（x－1） ③  213 a 28、3 29、4x 30、－x 31、 aaa 1223 23  32、2－2x 33、0 或 4 34、……=3ab－10 2b = ……=－87 35、周长等于 102529  36、AC=5,  ABC 的面积 等于 6 37、AE=20 题号 1 2 3 4 5 6 7 8 9 10 11 12 13 答案 B C B D D D D A D A A B D 题号 14 15 16 17 18 19 20 21 22 23 24 25 26 答案 3X－ 1 2.4 cm 3ab 0 5 x 14  1 2009 8 1 16 1 20 7； 45 附加题：(每小题 10 分,共 20 分) 1、（1） BAD 135 0 （2）四边形 ABCD 的面积（结果保留根号）=  122 1  2、(1)答案不唯一如：132－112=8×6，152－132=8×7 等 (2)任意两个奇数的平方差是 8 的倍数 (3 )证明： 设 m、n 为整数，则两个奇数可表示为 2m+1、2n+1， 则（2m+1）2 －（2n+1）2 = 4（m － n）（m + n+1） 当 m、n 同是奇数或偶数时，m － n 一定为偶数，所以 4（m － n）一定是 8 的倍数 当 m、n 一奇一偶时，（m + n+1）一定为偶数，所以 4（m + n+1）一定是 8 的倍数 综上：任意两个奇数的平方差是 8 的倍数。 八年级（上）数学期中试卷 （A卷）本卷共计100分 一、填空题(每题3分，共24分) 1.不等式x-3<1的正整数解是_____________． 2． 如右图所示的不等式的解集是___________． 3．一件商品的进价500元，标价为600元，打折销售后要保证获利不低于8%，则此商品最 多打 折． 4．四边形ABCD中，∠A∶∠Ｂ∶∠Ｃ∶∠Ｄ＝1∶2∶3∶4，则四边形ABCD是______形; 5．菱形的一个内角是120°，平分这个内角的一条对角形长是８，则菱形的周长是_______． 6．已知平行四边形的周长是28，一组邻边之比是3∶4，则这组邻边长分别是________． 7．矩形ABCD的对角线AC、BD相交于点O，∠BOC=２∠AOB，若AC=18cm，则CD=______cm． 8.如图，矩形ABCD的两条对角线交于点O，AC=5cm，点E、F分别是BC、 CD的中点，△BOE沿射线BD方向平移______cm可得到△ODF． 二、选择题（每题3分，共24分） 9．不等式3-2x>0的解集是（ ） 2 3)(2 3)(2 3)(2 3)(  xDxCxBxA 1 0. ( )   x-1>0不等式组 的解集是2x-5<1 ． ( ) 1 ( ) 3 ( ) ( ) 3 1A x B x C D x   无解 11．下列说法中，正确的个数是（ ）． （1）圆既是轴对称图形，又是旋转对称图形，也是中心对称图形 （2）旋转对称图形又是中心对称图形 （3）一个平行四边形是轴对称图形，但不是旋转对称图形 （4）中心对称图形又是旋转对称图形 （A）1个 （B）2个 （C）3个 （D）4个 D C B A O F E 12．在角、线段、等腰三角形、等边三角形、平行四边形、长方形、正方形、圆这八种图形 中，既是轴对称图形又是中心对称图形的共有（ ）． （Ａ）３个 （Ｂ）４个 （Ｃ）５个 （Ｄ）６个 13．在下面的五幅图案中，平移（1）可得到（Ａ）、（Ｂ）、（Ｃ）、（Ｄ）中的图案的是（ ）． 14．不能判定一个四边形是平行四边形的是（ ）． （Ａ）一组对边平行，另一组对边相等;（Ｂ）两组对边分别平行 （Ｃ）一组对边平行且相等; （Ｄ）两组对角分别相等 15．在等腰梯形、直角梯形、平行四边形、矩形、菱形、正方形中，对角线相等的四边形 有 （ ）。 （Ａ）４个 （Ｂ）３个 （Ｃ）２个 （Ｄ）１个 16．在平行四边形ABCD中，∠A比∠B大30°，则∠D为（ ）． （Ａ）45° （Ｂ）75° （Ｃ）90° （Ｄ）105° 三、解答题 17．解下列不等式（组）。（每小题5分，共20分） (1) 3x -2(1+2x)≥1,(解集请在数轴上表示出来) 3 2 5(2) 13 5 x x   ; （3） 2 1 3 3 1 x x       （4） 5 1 3 4 1 2 3 3 x x x x      18．（8分）如图，现有直角梯形与直角三角形各一个．请你通过平移、旋转运动，把这两个 图形组合成平行四边形、长方形、直角三角形，并画出组合后的图形． 19．（8分）已知在平行四边形ABCD中，Ｅ、Ｆ分别是AB、CD上的两个点，且BE=DF，试说明 AF、CE之间的关系． D C B A F E 20．（8分）如图，等腰梯形ABCD，AD∥BC，点E是底边BC上的一点，且DE∥AB，BC－AD＝AB， 请你来求一求∠B的度数． 21．（8分）学校举行奥数选拔赛，出线分数是66分．试卷上共有20题，做对一题得５分，做 错一题倒扣２分，不做得０分．王明有4题末做，问王明至少要答对多少题才有出线资格？ D C B A E B卷(本卷共计50分) 一、填空、选择题:（每小题5分，共计20分） 22.请你补全右图图案（使补全的图案成为中心对称图形） 23． 如图，点E是正方形ABCD对角线BD上的一点，且DE=AB，则∠BCE=________． 24．已知关于x的不等式 2 3x a   的解集如图，则a的值等于（ ） （Ａ）2 （Ｂ）1 （Ｃ）1 （Ｄ）0 25．在下列由纸折叠而成的图案中，是中心对称图形的是（ ）． 二、解答题： 26．（10分）m取何值时，关于x的方程2(x-1)=3x+m的解是负数？ 27．（10分）在△ACD中，∠D=90°，∠D的平分线交AC于点E，EF⊥AD交AD于点F，EG⊥DC交 DC于点G，请你说明四边形EFDG是正方形． 28．（10分）阅读并思考：△ABC、△EBF都是等腰直角三角形， (1)按如图a拼成一个图形，Ａ、Ｂ、Ｅ在一直线上，那么AF=EC． 理由：△ABC、△EBF都是等腰直角三角形, 所以AB=BC，BF=BE，∠ABC=∠EBF=90°, 故若将△ABF绕点B按顺时针方向旋转90°, 则有AB与BC重合，BF与BE重合, 即△ABF与△CBE重合, 所以AF=EC. (2)按如图b拼成另一个图形，请问AF与EC还相等吗？并说明理由． (3)按如图c拼成又一个图形，请问AF与EC还相等吗？ (4)请你仿照上面，将两个正方形也进行拼图编题并说理． 参考答案 一、填空题 1． 3 , 2 , 1 2． 2x  3．9 4．梯形 5． 32 6．6 和 8 7．9 8．2.5 二、选择题 9．C 10． D 11．B 12．B 13．D 14． A 15． A 16．B 三、解答题 517. (1) 3 (2) 6x x   数轴略 (3)无解 (4) 3 12 x   19．AF、CE 平行且相等 20．60° 21．14 B 卷 一、 22、略 23、22．5 度 24．C 25．D 26．m 2  27．略 28．略 八年级上册期中考试数学试卷 一、选择题（每小题 3 分，共 30 分） 1.如图，BE=CF，AB=DE，添加下列哪些条件可以推证△ABC≌△DFE（ ） A.BC=EF B. ∠A=∠D C.AC∥DF D.AC=DF 2.已知，如图，AC=BC，AD=BD，下列结论不正确的是 （ ） A.CO=DO B.AO=BO C.AB⊥CD D. △ACO≌△BCO （第 1 题图） （第 2 题图） 3.在△ABC 内取一点 P 使得点 P 到△ABC 的三边距离相等，则点 P 应是△ABC 的 哪三条线交点 （ ） A.高 B.角平分线 C.中线 D.垂直平分线 4. △ABC≌△DEF，AB=2，BC=4 若△DEF 的周长为偶数，则 DF 的取值为（ ） A.3 B.4 C.5 D.3 或 4 或 5 5.下列条件能判定△ABC≌△DEF 的一组是 （ ） A. ∠A=∠D，∠C=∠F，AC=DF B.AB=DE，BC=EF，∠A=∠D C. ∠A=∠D，∠B=∠E，∠C=∠F D.AB=DE，△ABC 的周长等于△DEF 的周长 6.下列图形中，不是轴对称图形的是 （ ） A.等边三角形 B.等腰直角三角形 C.四边形 D.线段 7.如下图，轴对称图形有 （ ） A.3 个 B.4 个 C.5 个 D.6 个 8.下列图形中，不是轴对称图形的是 （ ） A.有两条边相等的三角形 B.有一个角为 45°的直角三角形 C.有一个角为 60°的等腰三角形 D.一个内角为 40°，一个内角为 110°的三角形 9.当你看到镜子中的你在用右手往左梳理你的头发时，实际上你是 （ ） A.右手往左梳 B.右手往右梳 C.左手往左梳 D.左手往右梳 10.下列条件中不能作出唯一直角三角形的是 （ ） A.已知两个锐角 B.已知一条直角边和一个锐角 C.已知两条直角边 D.已知一条直角边和斜边 二、填空题（每小题 3 分，共 30 分） 11.已知，如图，AD=AC，BD=BC，O 为 AB 上一点，那么图中共有 对全 等三角形. . 12.如图，△ABC≌△ADE，若∠BAE=120°，∠BAD=40°，则∠BAC= . （第 11 题图） （第 12 题图） （第 13 题图） 13.如图，在△AOC 与△BOC 中，若∠1=∠2，加上条件 则有 △AOC≌△BOC. 14.如图所示，在△ABC 中，∠A=90°，BD 平分∠ABC，AD=2 ㎝， 则点 D 到 BC 的距离为 ㎝. 15.如图，AE=BF，AD∥BC，AD=BC，则有△ADF≌ . 16.如图，在△ABC 与△DEF 中，如果 AB=DE，BE=CF，只要加上 ∥ ， 就可证明△ABC≌△DEF. 17.点 P（5，―3）关于 x 轴对称的点的坐标为 . 18.如图，∠AOB 是一建筑钢架，∠AOB=10°，为使钢架更加稳固，需在内部添加 一些钢管 EF、FG、GH、HI、IJ，添加钢管的长度都与 OE 相等，则∠BIJ= . 19.等腰三角形一腰上的高与另一腰的夹角为 60°，则这个等腰三角形的顶角的度 数是 . 20.一个等腰三角形有两边分别为 5 和 8 ㎝，则周长是 厘米. ww w.x k b1.c o m 三、证明题（每小题 5 分，共 10 分） 21.如图，AB=DF，AC=DE，BE=FC，求证：∠B=∠F 22.如图，已知 AB=AC，AD=AE，BE 与 CD 相交于 O， 求证：△ABE≌△ACD. （第 14 题图） （第 15 题图） （第 16 题图） （第 18 题图） 四、解答题（每小题 6 分，共 12 分） 23.如图，在△ABC 中，∠ACB=90°，DE 是 AB 的垂直平分线， ∠CAE ：∠EAB=4：1，求∠B 的度数. www .xkb 1.com 24.如图，某地有两所大学和两条交叉的公路.图中点 M、N 表示大学，OA，OB 表示公路，现计划修建一座物资仓库，希望仓库到两所大学的距离相同，到两条 公路的距离也相同，你能确定出仓库 P 应建在什么位置吗？请在图中画出你的设 计.（尺规作图，不写作法，保留作图痕迹） 五、解答题（每小题 7 分，共 14 分） 25.已知：AD⊥BE，垂足 C 是 BE 的中点，AB=DE，则 AB 与 DE 有何位置关系？请 说明理由. 26.已知：在△ABC 中，AB=AC=2a ，∠ABC=∠ACB=15° 求：S△ABC. X-k-b-1.-c-o-m 六、解答题（每小题 7 分，共 14 分） 27.画出△ABC 关于 x 轴对称的图形△A1B1C1，并指出△A1B1C1 的顶点坐标. 28.已知：如图，△ABC 中，AB=AC，D 点在 AB 上，E 点在 AC 的延长线上，且 BD=CE， 连接 DE，交 BC 于 F.求证：DF=EF. 六、解答题（每小题 10 分，共 20 分） 29.如图：AB=AD，∠ABC=∠ADC，EF 过点 C，BE⊥EF 于 E，DF⊥EF 于 F， BE=DF.求证：CE=CF 30.如图，已知点 B、C、D 在同一条直线上，△ABC 和△CDE 都是等边三角形， BE 交 AC 于 F，AD 交 CE 于 H，求证：FH∥BD. 新课标第一网 参考答案 1.D；2.A；3.B；4.B；5.A；6.C；7.B；8.D；9.D；10.A11.3；12.80°；13.AO=BO； 14.2； 15. △CBE；16.AB∥DE；17.（5，3）；18.60°；19.15°或 30°；20.18 或 21； 21. 证明： ∵BE=CF ∴BE+CE=CF+CE ∴BC=EF 在△ABC 和△FED 中 AB=DF AC=DE BC=EF ∴△ABC≌△FED ∴∠B=∠F 22. 在△ABE 和△ACD 中 AE=AD ∠A=∠A AB=AC ∴△ABE 和△ACD 23.解：∵DE 是线段 AB 的垂直平分线 ∴AE=BE ∴∠B=∠EAD 设∠B= x 度，则∠CAE=4 x ∴4 x + x + x =180 ∴ x =30 24. 25. 解：AB∥DE ∵C 是 BE 的中点 ∴BC=CE ∵AD⊥BE ∴∠ACE=∠ECD=90° 在 Rt△ABC 和 Rt△DEC 中 AB=DE BC=CE ∴△ABC≌△DEC ∴∠B=∠E ∴AB∥ED 26. 27.A1（3，－4）；B1（1，－2）；C1 （5，－1） 解：延长 BA，过点 C 作 CD⊥AD， ∵AB=AC ∴∠B=∠C=15° ∵∠DAC 是△ABC 的外角 ∴∠DAC=30° ∴CD= 2 1 AC=a 新课|标 第|一|网 ∴S△ABC= 2 1 AB·C= 2 1 ×2a ×a = 2a 28.证明：过点 D 作 DN∥AE，交 BC 于点 N ∵AB=AC∴∠B=∠ACB ∵DN∥AE∴∠B=∠DNB∴BD=DN，∠E=∠NDE， 又∵BD=CE∴DN=CE 在△NDF 和△CEF 中 ∠DFN=∠CFE ∠NDE=∠E DN=CE ∴在△NDF≌△CEF ∴DF=EFX-k-b-1.-c- o-m 29.证明：连接 BD ∵AB=AC∴∠ABD=∠ADB 又∵∠ABC=∠ADC ∴∠ABC－∠ABD=∠ADC－∠ADB ∴∠DBC=∠BDC ∴BC=CD 在 Rt△BCE 和 Rt△DCF 中 BC=CD BE=DF ∴Rt△BCERt≌△DCF ∴EC=CF 30. ∵△ABC 和△CED 为等边三角形 ∴BC=AC，CE=CD，∠FCH=∠ACB=∠ECD=60° 在△ACD 和△BCE 中 AC=BC ∠ACD=∠BCE=120° CD=CE 在△BFC 和△ACH 中 ∠CAD=∠CBE BC=AC ∠BCF=∠ACH ∴△BFC≌△ACH ∴CF=CH 又∵∠ACE=60° ∴△FCH 为等边三角形 ∴∠HFC=60° ∴FH∥BD 八年级期中考试 数学试题（无答案） （全卷总分 150 分 考试时间 120 分钟 命题人：谢耀清） A 卷 26、选择题：（每题 3 分,共 21 分） 1、36 的平方根是 （ ） A、－6 B、36 C、± 6 D、±6 2、下列各式中，计算正确的是（ ） A． 623 xxx  B． 333 2aaa  C． 632 mmmm  D． 33 ccc  3、下列各组数中不能作为直角三角形的三边长的是 （ ） A. 1.5, 2, 3; B. 7, 24, 25; C. 6, 8, 10; D. 9, 12, 15. 4、数 3.14， 2 ， ，0.323232…， 7 1 ， 9 中，无理数的个数为（ ）． A、2 个 B、 3 个 C、4 个 D、5 个 5、线段 AB 是由线段 CD 经过平移得到的，则线段 AB 与线段 CD 的关系为（ ） A、相交 B、平行或相等 C、平行且相等 D、平行（或在同一直线上） 且相等 6、不能用平方差公式计算的是（ ） A (m+n)(m-n) B (-m+n)(m+n) C (-m+n)(m-n) D (-m+n)(-m-n) 7、下列语句正确的有（ ）个 ① -1 是 1 的平方根 ② 带根号的数都是无理数 ③ -1 的立方根是-1 ④4 的算 术平方根是 2 A 1 B 2 C 3 D 4 二、填空题（每题 2 分,共 20 分） 8、计算：  34 43 xx ； 9、计算： 2( 9 3 ) ( 3 )x x x     ； 10、因式分解： 2 1x   ； 11、多项式 2 26 3a b ab 的公因式是 12、－8 的立方根是 。 13、直角三角形两条直角边的长分别为 5、12，则斜边长为 . 14、如右图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最 大的正方形的边长为 7cm ，则正方形 A，E，C，D 的面积之和为 （第 14 题） （第 15 题） （第 16 题） （第 17 题） 15、如图，△ABC 沿 BC 方向平移到△DEF 的位置，若 EF=5cm，CE=2cm，则平移 的距离是 16、如图，在水塔 O 的东北方向 32m 处有一抽水站 A，在水塔的东南方向 24m 处有一建筑工地 B，在 AB 间建一条直水管，则水管的长为___________. 17、如图 AB=BC=CD=DE=1，AB⊥BC，AC⊥CD，AD⊥DE，则 AE 等于 . 三、解答题：（共 59 分） 18、（2 小题，每题 4 分，共 8 分） ①利用公式计算：999×1001 ②因式分解：x2－5x－6 19、（4 小题，每题 5 分，共 20 分） ① 计算： 2332 )3 1()3( acba  ②计算： )2)(2()4( yxyxyxx  ③ 计算：    aaba 365 223  ④因式分解： aaa 96 23  20、先化简再求值：（5 分） 2( 2 ) ( )( 4 )a b a b a b    ，其中 7200 1a ， 7200b E D A C 7cm A B 东 南 西 北 O B C A D E 21、（5 分）平移方格纸中的△ABC，使点 A 平移到点 D 处，画出平移后的△DB 1 C 1 ， 然后在将平移后的三角形按顺时针方 向绕点 D 旋转 90 0 ，再画出旋转后的三 角形 22、（6 分）如图，已知 CD＝6m， AD＝8m， ∠ADC＝90°， BC＝24m， AB＝26m．求 图中阴影部分的面积． （第 22 题） （第 23 题） 23、（7 分）如图△ABC 中，BC＝10，AC=17，CD=8，BD=6。求（1）AD 的长，（2） △ABC 的面积 24、(8 分)“中华人民共和国道路交通管理条例”规定：小汽车在城街路上行驶 速度不得超过70 千米/小时。如图，一辆小汽车在一条城市街路上直道行驶，某 一时刻刚好行驶到路面对车速检测仪 A 正前方30米 C 处，过了2 秒后，测得小汽 车与车速检测仪间距离为50米。 请问这辆小汽车超速了吗？为什么？ （第 24 题） （第 25 题） B 卷 四、填空题（每题 4 分，共 20 分） 25、一只蚂蚁从长、宽都是 3，高是 8 的长方体纸箱的 A 点沿纸箱爬 到 B 点，那么它所行的最短路线的长是 。 26、一个矩形的面积是 3(x2-y2) , 如果它的一边长为( x+ y) , 则它的另一边 长是______. C B D A B 观 测 小 汽小 汽 B C A A B 27、若 12)()3( 2  nxxmxx ，则 m ， n 28、请你观察、思考下列计算过程： 因为 121112  ，所以 11121  ，同样，因为 123211112  ，所以 11112321  ，…， 由此猜想 76543211234567898 =_________________． 29、 162  mxx如果 是一个完全平方式，那么 m 。 五、解答题：（共 30 分） 30、（5 分）已知：3x=2，3y=5，求 3x+2y 的值 31、（6 分）已知（x+y）2=1,(x-y) 2=49，求 x2+y2 与 xy 的值. 32、（6 分）已知 2 1a  的平方根是±3，3 1a b  的算术平方根是 4，求 2a b 的 平方根。 33、（6 分）为了丰富少年儿童的业余生活，某社区要在如图所示 AB 所在的直线 建一图书室，本社区有两所学校所在的位置在点 C 和点 D 处，CA⊥AB 于 A，DB ⊥AB 于 B，已知 AB = 25km，CA = 15 km，DB = 10km，试问：图书室 E 应该建 在距点 A 多少 km 处，才能使它到两所学校的距离相等? 34、（7 分）如图，一根 5m 长的竹杆 AB，斜靠在一竖直的墙 AO 上，这时 AO 的距 离为 4m，如果（1）竹杆的顶端 A 沿墙下滑 0.5m，那么竹竿底端 B 也外移 0.5m 吗？（2）当竹竿的顶端 A 沿墙下滑 1m 时，那么竹竿底端 B 又如何移动？ 厦门市东山中学 2008—2009 学年第一学期 07 级初二期中考试 数学科答题卷 B D EA x （全卷总分 150 分 考试时间 120 分钟 命题人：谢耀清） 题 号 A 卷（100 分） B 卷（50 分） A 卷 B 卷 总 分一 二 三 四 五 1 8 1 9 2 0 2 1 2 2 2 3 2 4 3 0 3 1 3 2 3 3 3 4 得 分 一、选择题：（每题 3 分，共 21 分） 题号 1 2 3 4 5 6 7 选项 二、填空题：（每题 2 分，共 20 分） 8、 9、 10、 11、 12、 13、 14、 15、 16、 17、 三、解答题：（共 59 分） 18、（每题 4 分，共 8 分） ①利用公式计算：999×1001 ②因式分解：x2－5x－6 19、（每题 5 分，共 20 分） ①计算： 2332 )3 1()3( acba  ②计算： )2)(2()4( yxyxyxx  ③计算：    aaba 365 223  ④因式分解： aaa 96 23  20、先化简再求值：（5 分） 2( 2 ) ( )( 4 )a b a b a b    ，其中 7200 1a ， 7200b 班 班 级 姓 名 座 号 21、（5 分）平移方格纸中的△ABC，使点 A 平移到点 D 处，画出平移后的△DB 1 C 1 ， 然后在将平移后的三角形按顺时针方 向绕点 D 旋转 90 0 ，再画出旋转后的三 角形 22、（6 分）如图，已知 CD＝6m， AD＝8m， ∠ADC＝90°， BC＝24m， AB＝26m．求 图中阴影部分的面积． 23、（7 分）如图△ABC 中，BC＝10，AC=17，CD=8，BD=6。求（1）AD 的长，（2） △ABC 的面积 24、(8 分)“中华人民共和国道路交通管理条例”规定：小汽车在城街路上行驶 速度不得超过70 千米/小时。如图，一辆小汽车在一条城市街路上直道行驶，某 一时刻刚好行驶到路面对车速检测仪 A 正前方30米 C 处，过了2 秒后，测得小汽 车与车速检测仪间距离为50米。请问这辆小汽车超速了吗？为什么？ C B D A B 观 测 小 汽小 汽 B C A B 卷 四、填空题（每题 4 分，共 20 分） 25、 26、 27、 m ， n 28、 29、 五、解答题：（共 30 分） 30、（5 分）已知：3x=2，3y=5，求 3x+2y 的值 31、（6 分）已知（x+y）2=1,(x-y) 2=49，求 x2+y2 与 xy 的值. 32、（6 分）已知 2 1a  的平方根是±3，3 1a b  的算术平方根是 4，求 2a b 的 平方根。 33、（6 分）为了丰富少年儿童的业余生活，某社区要在如图所示 AB 所在的直线 建一图书室，本社区有两所学校所在的位置在点 C 和点 D 处，CA⊥AB 于 A，DB ⊥AB 于 B，已知 AB = 25km，CA = 15 km，DB = 10km，试问：图书室 E 应该建 在距点 A 多少 km 处，才能使它到两所学校的距离相等? B D EA x c 34、（7 分）如图，一根 5m 长的竹杆 AB，斜靠在一竖直的墙 AO 上，这时 AO 的距 离为 4m，如果（1）竹杆的顶端 A 沿墙下滑 0.5m，那么竹竿底端 B 也外移 0.5m 吗？（2）当竹竿的顶端 A 沿墙下滑 1m 时，那么竹竿底端 B 又如何移动？ 八年级第一学期期中考试数学试题 （考试时间：120 分钟 满分：150 分） 一、选择题（共 8 小题，每小题 3 分，共 24 分） 1．下面的图形中，不是轴对称图形的是（ ） A B C D 2．下列计算正确的是（ ） A． 24  B． 3273  C． 4)4( 2  D． 393  3．下列各组中的三条线段不能．．构成直角三角形的是（ ） A．3，4，5 B．1，2， 5 C．5，7，9 D．7，24，25 4．一个等腰三角形的两边长分别是 3 和 7，则它的周长为（ ） A．17 B．15 C．13 D．13 或 17 5．下列说法正确的是（ ） A．无限小数都是分数 B． 16 表示 4 的算术平方根 C．平方根等于本身的数是 0 D．数轴上的每一个点都表示一个有理数 6．到三角形的三个顶点距离相等的点是（ ） A．三条角平分线的交点 B．三条中线的交点 C．三条高的交点 D．三条边的垂直平分线的交点 7．如图，在 Rt△ABC 中，∠ACB=90°，E 是 AB 上一点，且 BE=BC，DE⊥AB 于 E，若 AC=8， 则 AD+DE等于（ ） A．7 B．8 C．9 D．10 8．如图，在△ABC 中，BD⊥AC，BD=AC，以 BC 为底边作等腰直角△BEC，连接 AE 并延长 交 BD 于 F 点，下列结论： ①△AEC≌△DEB ；②AE⊥DE；③DE=DC；④ CDEAEB SS   ． 其中正确的有（ ）个 A.1 B.2 C.3 D.4 二、填空题（共 10 小题，每小题 3 分，共 30 分） 9．比较大小： 5 7 10． 3.1415926 精确到百分位的结果为 . 11．某人站在小河边，从河面上看到河对岸巨型电子屏上显示的时间，其读数 如图所示，则该电子屏显示的实际时刻是 ． 12．若一个正数的平方根是 12 a 和 2 a ，则这个正数是 ． 13．一个直角三角形的两条直角边长分别为 5、12，则斜边上的中线长为 ． 14．如图，将 Rt△ABC 绕直角顶点顺时针旋转 90°，得到△A′B′C，连结 AA′，若∠AA′B′=20°， 则∠B的度数为 °． 15．如图，以数轴的单位长度为边作正方形，以数轴上的原点 O 为圆心，正 方形的对角线 的长为半径作弧与数轴交于一点 A，则点 A 表示的数为 ． 16．Rt△ABC 的三边分别为 a ，b ， c ，且 50222  cba ，则斜边 c ． 第 7 题图 第 8 题图 第 17 题图第 15 题图第 14 题图 17．如图，AD 是△ABC 中∠BAC 的角平分线，DE⊥AB 于点 E， 7ABCS ，DE=2，AB=4， 则 AC 长为 ． 18．同一平面上，两个等边三角形组成的各种图案，最多有 条对称轴． 三、解答题（共 96 分） 19．（本题 8 分）求下列各式中的 x (1) 42 x (2) 054)1(2 3 x 20．（本题 8 分）计算 (1) 23 )3(836  (2)  0 2 3 1 2 4    21．（本题 8 分）尺规作图 如图，已知∠AOB 和 C、D 两点，求作一点 P，使 PC=PD，且 P 到∠AOB 两边的距离相等．(不 写画图过程，保留作图痕迹) 22．（本题 8 分）已知 yx 2 的平方根为 3 ， 2 是 y的立方根，求 xy4 的平方根． 23．（本题 10 分）如图，正方形网格中的每个小正方形边长都是 1，每个小格的顶点叫做格 点，若△ABC 的三个顶点都在格点上，且 AB、BC、AC 三边的长分别为 5 、 10 、 13 ． （1）请在正方形网格中画出一个符合条件的格点△ABC； （2）求△ABC 的面积． 第 23 题图 第 21 题图 24．（本题 10 分）如图，AD、BC 相交于 O，OA=OC，∠OBD=∠ODB．求证：AB=CD． 25．（ 本题 10 分） 如图，将在 Rt△ABC 绕其锐角顶点 A 旋转 90°得到 Rt△ADE，连接 BE， 延长 DE、BC 相交于点 F，则有∠BFE=90°，且四边形 ACFD 是一个正方形． （1）判断△ABE 的形状，并证明你的结论； （2）用含 b 的代数式表示四边形 ABFE 的面积； 26．（ 本题 10 分 ） 如图，在△ABC 中，AB=AC，点 D、E、F 分别在 AB、BC、AC 边上，且 BE=CF，BD=CE． （1）求证：△DEF 是等腰三角形； （2）当∠A=40°时，求∠DEF 的度数． A D B CE F 第 25 题图 27．（本题 12 分）如图，将长方形纸片 ABCD 沿着 EF 折叠，使得点 C 与点 A 重合． （1）求证：AE=AF； （2）若 AB=3，BC=9，试求 CF 的长； （3）在（2）的条件下，试求 EF 的长． 28．（本题 12 分） 如图，△ABC 和△CDE 均为等腰三角形，AC=BC，CD=CE，AC>CD，∠ACB=∠DCE 且点 A、D、 E 在同一直线上，连接 BE． （1）若∠ACB=60°, 则∠AEB 的度数为 ； 线段 AD、BE 之间的数量关系是 ． （2）若∠ACB=∠DCE=90°, CM 为△DCE 中 DE 边上的高． ①求∠AEB 的度数． ②若 2AC ， 1BE ，试求 CM 的长．（请写全必要的证明和计算过程） 第 28 题图 第 27 题图 八年级期中试题参考答案 一、选择题 1~8 BBCA CDBC 二、填空题 9. > 10. 3.14 11. 12:01 12. 9 13. 2 13 14. 65 15. 2 16. 5 17. 3 18. 6 三、解答题 19. (1) 2x (2) 4x 20. (1) 7 (2) 24  21. 提示：作 CD 垂直平分线与∠AOB 的角平分线的交点 22. 根据题意得： 8)2( 3 y ， 92  yx ，所以 2 1x ，因而 164  xy 16 的平方根是 4 23.（1） (2) 2 7 24. ∵∠OBD=∠ODB，∴OB=OD， 在△ABO 和△CDO 中： ∵OA=OC，∠AOB=∠COD，OB=OD ∴△ABO≌△CDO（SAS） ∴AB=CD 25. （1）等腰直角三角形，证明过程略； （2） 2 2 )( 2 bbbababSSS ACFEABCABFE   第 23 题图 A B C 26.（1）证明：∵AB=AC，∴∠B=∠C 在△BDE 和△CEF 中： ∵BD=CE，∠B=∠C，BE=CF ∴△BDE≌△CEF（SAS） ∴DE=EF， ∴△DEF 是等腰三角形 （2）解：∵∠DEC=∠B+∠BDE， 即∠DEF+∠CEF=∠B+∠BDE 由（1）知△BDE≌△CEF， 则∠BDE=∠CEF ∴∠DEF=∠B ∵∠A=40° ∴∠B=∠C= 2 40180 00  =70° ∴∠DEF=70° 27. （1）∵折叠 ∴∠AFE=∠CFE ∵AD//BC ∴∠AEF=∠CFE ∴∠AEF=∠AFE ∴AE=AF （2）设 xCF  ，则 xBF  9 ， xAF  根据勾股定理得： 222 )9(3 xx  解得： 5x 即 5CF （3） 10 28.（1）60° AD=BE （2）①∠AEB=90° ② 2 13  八年级数学第一学期期中考试 （考试时间：120 分钟 满分：150 分） 一、选择题（共 8 小题，每小题 3 分，共 24 分） 1．下面的图形中，不是轴对称图形的是（ ） A B C D 2．下列计算正确的是（ ） A． 24  B． 3273  C． 4)4( 2  D． 393  3．下列各组中的三条线段不能．．构成直角三角形的是（ ） A．3，4，5 B．1，2， 5 C．5，7，9 D．7，24，25 4．一个等腰三角形的两边长分别是 3 和 7，则它的周长为（ ） A．17 B．15 C．13 D．13 或 17 5．下列说法正确的是（ ） A．无限小数都是分数 B． 16 表示 4 的算术平方根 C．平方根等于本身的数是 0 D．数轴上的每一个点都表示一个有理数 6．到三角形的三个顶点距离相等的点是（ ） A．三条角平分线的交点 B．三条中线的交点 C．三条高的交点 D．三条边的垂直平分线的交点 7．如图，在 Rt△ABC 中，∠ACB=90°，E 是 AB 上一点，且 BE=BC，DE⊥AB 于 E，若 AC=8， 则 AD+DE等于（ ） A．7 B．8 C．9 D．10 8．如图，在△ABC 中，BD⊥AC，BD=AC，以 BC 为底边作等腰直角△BEC，连接 AE 并延长 交 BD 于 F 点，下列结论： ①△AEC≌△DEB ；②AE⊥DE；③DE=DC；④ CDEAEB SS   ． 其中正确的有（ ）个 A.1 B.2 C.3 D.4 二、填空题（共 10 小题，每小题 3 分，共 30 分） 9．比较大小： 5 7 10． 3.1415926 精确到百分位的结果为 . 11．某人站在小河边，从河面上看到河对岸巨型电子屏上显示的时间，其读数 如图所示，则该电子屏显示的实际时刻是 ． 12．若一个正数的平方根是 12 a 和 2 a ，则这个正数是 ． 13．一个直角三角形的两条直角边长分别为 5、12，则斜边上的中线长为 ． 14．如图，将 Rt△ABC 绕直角顶点顺时针旋转 90°，得到△A′B′C，连结 AA′，若∠AA′B′=20°， 第 7 题图 第 8 题图 则∠B的度数为 °． 15．如图，以数轴的单位长度为边作正方形，以数轴上的原点 O 为圆心，正 方形的对角线 的长为半径作弧与数轴交于一点 A，则点 A 表示的数为 ． 16．Rt△ABC 的三边分别为 a ，b ， c ，且 50222  cba ，则斜边 c ． 17．如图，AD 是△ABC 中∠BAC 的角平分线，DE⊥AB 于点 E， 7ABCS ，DE=2，AB=4， 则 AC 长为 ． 18．同一平面上，两个等边三角形组成的各种图案，最多有 条对称轴． 三、解答题（共 96 分） 19．（本题 8 分）求下列各式中的 x (1) 42 x (2) 054)1(2 3 x 20．（本题 8 分）计算 (1) 23 )3(836  (2)  0 2 3 1 2 4    21．（本题 8 分）尺规作图 如图，已知∠AOB 和 C、D 两点，求作一点 P，使 PC=PD，且 P 到∠AOB 两边的距离相等．(不 写画图过程，保留作图痕迹) 22．（本题 8 分）已知 yx 2 的平方根为 3 ， 2 是 y的立方根，求 xy4 的平方根． 第 17 题图第 15 题图第 14 题图 第 21 题图 23．（本题 10 分）如图，正方形网格中的每个小正方形边长都是 1，每个小格的顶点叫做格 点，若△ABC 的三个顶点都在格点上，且 AB、BC、AC 三边的长分别为 5 、 10 、 13 ． （1）请在正方形网格中画出一个符合条件的格点△ABC； （2）求△ABC 的面积． 24．（本题 10 分）如图，AD、BC 相交于 O，OA=OC，∠OBD=∠ODB．求证：AB=CD． 25．（ 本题 10 分） 如图，将在 Rt△ABC 绕其锐角顶点 A 旋转 90°得到 Rt△ADE，连接 BE， 延长 DE、BC 相交于点 F，则有∠BFE=90°，且四边形 ACFD 是一个正方形． （1）判断△ABE 的形状，并证明你的结论； （2）用含 b 的代数式表示四边形 ABFE 的面积； 第 23 题图 第 25 题图 26．（ 本题 10 分 ） 如图，在△ABC 中，AB=AC，点 D、E、F 分别在 AB、BC、AC 边上，且 BE=CF，BD=CE． （1）求证：△DEF 是等腰三角形； （2）当∠A=40°时，求∠DEF 的度数． 27．（本题 12 分）如图，将长方形纸片 ABCD 沿着 EF 折叠，使得点 C 与点 A 重合． （1）求证：AE=AF； （2）若 AB=3，BC=9，试求 CF 的长； （3）在（2）的条件下，试求 EF 的长． 28．（本题 12 分） 如图，△ABC 和△CDE 均为等腰三角形，AC=BC，CD=CE，AC>CD，∠ACB=∠DCE 且点 A、D、 E 在同一直线上，连接 BE． （1）若∠ACB=60°, 则∠AEB 的度数为 ； 线段 AD、BE 之间的数量关系是 ． （2）若∠ACB=∠DCE=90°, CM 为△DCE 中 DE 边上的高． ①求∠AEB 的度数． ②若 2AC ， 1BE ，试求 CM 的长．（请写全必要的证明和计算过程） A D B CE F 第 28 题图 第 27 题图 八年级期中试题参考答案 四、选择题 1~8 BBCA CDBC 五、填空题 9. > 10. 3.14 11. 12:01 12. 9 13. 2 13 14. 65 15. 2 16. 5 17. 3 18. 6 六、解答题 19. (1) 2x (2) 4x 20. (1) 7 (2) 24  21. 提示：作 CD 垂直平分线与∠AOB 的角平分线的交点 22. 根据题意得： 8)2( 3 y ， 92  yx ，所以 2 1x ，因而 164  xy 16 的平方根是 4 23.（1） (2) 2 7 24. ∵∠OBD=∠ODB，∴OB=OD， 在△ABO 和△CDO 中： ∵OA=OC，∠AOB=∠COD，OB=OD ∴△ABO≌△CDO（SAS） ∴AB=CD 25. （1）等腰直角三角形，证明过程略； （2） 2 2 )( 2 bbbababSSS ACFEABCABFE   第 23 题图 A B C 26.（1）证明：∵AB=AC，∴∠B=∠C 在△BDE 和△CEF 中： ∵BD=CE，∠B=∠C，BE=CF ∴△BDE≌△CEF（SAS） ∴DE=EF， ∴△DEF 是等腰三角形 （2）解：∵∠DEC=∠B+∠BDE， 即∠DEF+∠CEF=∠B+∠BDE 由（1）知△BDE≌△CEF， 则∠BDE=∠CEF ∴∠DEF=∠B ∵∠A=40° ∴∠B=∠C= 2 40180 00  =70° ∴∠DEF=70° 27. （1）∵折叠 ∴∠AFE=∠CFE ∵AD//BC ∴∠AEF=∠CFE ∴∠AEF=∠AFE ∴AE=AF （2）设 xCF  ，则 xBF  9 ， xAF  根据勾股定理得： 222 )9(3 xx  解得： 5x 即 5CF （3） 10 28.（1）60° AD=BE （2）①∠AEB=90° ② 2 13  八年级第一学期期中考试数学试题 说明：本试题满分 120 分，考试时间 100 分钟。 一、选择题（每小题 3 分，共 36 分） 1．若等腰三角形的底角为 54°，则顶角为 A．108° B．72° C．54° D．36° 2．下列各式由左边到右边的变形，属于因式分解的是 A． baaba  326 2 B． 1)2(122  xxxx C． ))((22 bababa  D． )()( yxbyxabybxayax  3．若分式 )2)(1( )2)(1(   xx xx 的值为 0，则 x 的值是 A．－l B．－l 或 2 C．2 D．－2 4．下列说法正确的是 A．轴对称图形的对称轴只有一条 B．角的对称轴是角的平分线 C．成轴对称的两条线段必在对称轴同侧 D．等边三角形是轴对称图形 5．下列式子中总能成立的是 A． 1)1( 22  aa B． 1)1)(1( 2  aaaa C． 1)1( 22  aaa D． 21)1)(1( aaa  6．如果把分式 yx x  中的 yx、 都扩大 3 倍，那么分式的值 A．扩大 3 倍 B．不变 C．缩小 3 倍 D．缩小 6 倍 7．若点 A（ a ，－l），与点 B（4，b ）关于 y 轴对称，则 A． 14  ba ， B． 14  ba ， C． 14  ba ， D． 14  ba ， 8．下列分解因式正确的是 A． )1( 23 aaaa  B． )(2242 baba  C． 22 )2(4  aa D． 22 )1(12  aaa 9．方程 2 4 2 1 2 1 2   xxx A． 2x B． 2x C．无解 D．以上都不对 10．如下图，CD 是 AB 的垂直平分线，AC＝1.6cm，BD＝2.3cm，则四边形 ACBD 的周长为 A．3.9cm B．8.8cm C．7.8cm D．无法计 算 11．一艘船顺流航行 s 千米用了 x 小时，如果逆流航速是顺流航速的 m n ，那么 这艘船逆流航行t 小时走的路程是 A． xm snt B． xn smt C． x st D． m xsnt 12．如果 22 )()( yxMyx  ，那么 M 等于 A． xy2 B． xy2 C． xy4 D． xy4 二、填空题（每题 3 分，共 15 分） 13．分解因 式  22 9yx ___________。 14．当 x ___________时，分式 9 9   x x 的值等于 0。 15．从汽车的后视镜中看见某车车牌的后 5 位号码是 ，该车牌的 5 位号码实际是 ___________。 16．一个矩形面积是 22 242 yxyx  ，一边长为 )(2 yx  ，则另一边长为___________。 17．观察下面一列分式， x 1 ， 2 2 x ， 3 4 x  ， 4 8 x ， 5 16 x  ，……，根据你的发现它的第 8 项是___________，第 n 项是___________。 三、解答题（18 题 9 分，其余各 12 分，共 69 分） 18．（9 分）如下图是由三个小正方形组成的“L”形图，请你用三种方法分别在图中添加一 个小正方形使它成为轴对称图形。 19．解分式方程（12 分） （1） 35 2 5 3   x x x （2） 1 1 4 1 1 2     xx x 20．化简：（12 分） （1） 11 2  mm m （2） xx   3 2 9 12 2 21．（12 分）如下图，在等腰三角形 ABC 中，AB＝AC，AB＋BC＝13，AB 边的垂直平分线 MN 交 AC 于点 D，求 ABCD 的周长。 22．（12 分）下图甲是一个长为 m2 ，宽为 n2 的长方形，沿图中虚线用剪刀均剪成四个小 长方形，然后按图乙所示拼成一个大正方形。 （1）写出图乙中的阴影部分的正方形的边长等于________（用含有 nm、 的式子表示）； （2）请用两种不同的方法求图乙中阴影部分的面积： 方法一： 方法二： （3）观察图乙，尝试写出 mnnmnm 、、 22 )( )(  三个式子之间的等量关系： _______。 （4）根据（3）题中的等量关系，解决如下问题：若 127  abba ， ，求式子 2)( ba  的值。 23．（12 分）某市在旧城改造过程中，需要整修一段全长 2400 米的道路，为了尽量减少施 工对城市交通所造成的影响，实际工作效率比原计划提高了 20%，结果提前 8 小时完成 任务，求原计划每小时修路的长度。 2011-2012 学年度阳谷县第一学期八年级期中考试 数学试题参考答案 一、选择题（3×12＝36 分） 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 B C C D D B B D C C A D 二、填空题（4×5＝20 分） 13． )3)(3( yxyx  14．－9 15．BA659 16． yx  17． 8 72 x ， n n n x 12)1(   三、解答题（共 69 分） 18．解析：要添加一个小正方形使它成为轴对称图形，关键是确定图形的对称轴，画法如下 图所示。 19．（1） 4x （2） 1x 20．（1） 1 1 m （2） 3 2  x 21．解：因为 MN 是线段 AB 的垂直平分线，且点 D 在 MN 上，所以 DA＝DB 所以△BCD 的周长＝BC＋CD＋BD＝BC＋AC 因为 AB＝AC，且 AB＋BC＝13， 所以△BCD 的周长＝BC＋AC＝AB＋BC＝13 22．（1） nm  （2）方法一： 2)( nm  方法二： mnnm 4)( 2  （3） mnnmnm 4)()( 22  （4） abbaba 4)()( 22  ∵ 127  abba ， … … 红 黄 绿 蓝 紫 红 黄 绿 黄 绿 蓝 紫 ∴ 11247)( 22  ba 23．解：依题意可设原计划每小时修路 x 米，则有： 8%)201( 24002400  xx ，解之得 50x 所以原计划每小时修 50 米。 八年级数学期中测试卷 1、2012 年奥运会火炬接力活动的传递总路程约为 137000000 米，这个数保留两个有效数字 并用科学记数法表示为 （ ） A． 1.37×108 米 B． 1.4×108 米 C．13.7×107 米 D． 14×107 米 2、以下列数组为边长中，能构成直角三角形的 （ ） A． 2 ， 3 ， 5 B．1，1， 3 C．0.2，0.3，0.5 D． 3 1 ， 4 1 ， 5 1 4、下列实数中， 7 1 、 3 11 、 2  、－3.14， 25 、 3 27 、0、0.3232232223… （相邻两个 3 之间依次增加一个 2），无理数的个数是 （ ） A．1 个 B．2 个 C．3 个 D．4 个 5、一个纸环链，纸环按红黄绿蓝紫的顺序重复排列，截去其中的一部分，剩下部分如图所 示，则被截去部分纸环的个数可能是 （ ） A．2010 B.2011 C.2012 D.2013 6 、 平 行 四 边 形 ABCD 的一组对 边和为 12 cm ，下列各组数据中可 以作为这个平行四边形两条对角线的 长度的是 （ ） A． cmcm 9,2 B． cmcm 8,3 C． cmcm 7,5 D． cmcm 7,6 7、将一正方形纸片按下列顺序折叠，然后将最后折叠的纸片沿虚线剪去上方的小三角形， 再将纸片展开，得到的图形是 （ ） 8、如图，在直线l 上依次摆放着七个正方形，已知斜放置的三个正方形的面积分别为 1， 1.21 ， 1.44 ， 正 放 置 的 四 个 正 方 形 的 面 积 为 S1 、 S2 、 S3 、 S4 ， 则 S1+S2+S3+S4= （ ） A. 3.65 B. 2.42 C. 2.44 D. 2.65 二、细心填一填：（每空 2 分，计 36 分） 9、 25 的平方根是 ，－27 的立方根是 ． 10、 81 的算术平方根是 ，比较大小： 2 15  2 1 ． 11、计算： 2)16( ＝________， 2)3(  ＝ ． 12、若 92 x ，且 x 没有平方根，则 x＝ ；若 23 y ，则 y＝ ． 13、在四边形 ABCD 中， AD ∥ BC ，对角线相交于点O ，请你再添加一个条件， ，使它成为一个平行四边形。（填写一种你认为适当的条件） 14、已知等腰三角形的一个外角等于 100°，则它的顶角为 ． 15、如图，在 ABCD 中，已知 AB＝6，BC＝8，BE 平分∠ABC 交 AD 于点 E，则 DE＝ ． 16、若一正数的两个平方根分别是 2a-1 与-a+2，则这个正数等于 . ] 17、如图，∠C ＝∠ ADE ＝70°，∠ B ＝∠ E ＝30°，BC＝ED，点 D 在 BC 上，那么将 ABC 绕着点 A 按 时针方向旋转 度就能与 AED 重合． 18、 如图，在 ABCD 中， AC、BD 相交于点 O，OE⊥AC 交 AD 于 E，若 AB＝4 cm ，BC ＝6 cm ，则 CED 的周长为 cm ． 19、如图， ABCD 的周长是 36，且 AB∶BC＝5∶4，对角线 AC、BD 相交于点 O，且 BD⊥AD， 则 BD＝________，AC＝ ． 三、解答题（40 分） 21、（每小题 3 分，共 6 分） （1）计算： 2 23( 6) 27 ( 5)   （2）求 x 的值：3(x－1)3+24=0 A B C DE （第 15 题图） O E D CB A （第 18 题图） D E C B A （第 17 题图） B O D C A （第 19 题图） 22、（本题满分 6 分）作图题：如图，在 66 的正方形网格中，每个小正方形的边长都为 1. 请在所给网格中按下列要求画出图形． （1）从点 A 出发的一条线段 AB，使它的另一个端点落在格点（即小正方形的顶 点） 上，且长度为 22 ；（2 分） （3）画出△ABC 关于点 B 的中心对称图形△A1B1C1．（2 分） 23、（本题满分 8 分）．如图，在 Rt OAB 中， 90OAB   ， 6OA AB  ，将 OAB 绕 点O 沿逆时针方向旋转 90 得到 1 1OA B ． （1）线段 1OA 的长是 ， 1AOB 的度数是 ；(每空 1 分，共 2 分) （2）连结 1AA ，判断四边形 1 1OAA B 的形状，并说明理由；(4 分) （3）求四边形 1 1OAA B 的面积．（2 分） 24、（本题满分 5 分）如图，某住宅小区在施工过程中留下了一块空地（图中的四边形 ABCD）， 经测量，在四边形 ABCD 中，AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°。小区为美化环境，欲 在空地上铺草坪，已知草坪每平方米 100 元，试问铺满这块空地共需花费多少元？ A 25、（本题满分 8 分）如图①，△ABC 中，∠B、∠C 的平分线交于 O 点，过 O 点作 EF∥BC 交 AB、AC 于 E、F． 试说明：EO＝BE 探究一：请写出图①中线段 EF 与 BE、CF 间的关系，并说明理由. 探究二：如图②，若△ABC 中∠B 的平分线 BO 与△ABC 的外角平分线 CO 交于 O，过 O 点作 EF∥BC 交 AB 于 E，交 AC 于 F．这时 EF 与 BE、CF 的关系又如何? 请直接写出关系 式，不需要说明理由. 1．如图，已知 AB=AC，E、D 分别在 AB、AC 上，BD 与 CE 交于点 F，且∠ABD= ∠ACE， 求证：BF=CF． F E C B O A ② F E C B O A ① E D C A B F 2．如图，△ABC 中 BA=BC，点 D 是 AB 延长线上一点，DF⊥AC 于 F 交 BC 于 E， 求证：△DBE 是等腰三角形． 3. 如图, 已知：点 D,E 在△ABC 的边 BC 上,AB=AC,AD=AE.求证：BD=CE 4. 如图：△ABC 中,AB=AC,PB=PC．求证：AD⊥BC 5. 已知：如图,BE 和 CF 是△ABC 的高线,BE=CF,H 是 CF、BE 的交点．求证： HB=HC E D C A B F 26、（本题满分 7 分）如图，矩形 ABCD 中，AB=4cm，BC=8cm，动点 M 从点 D 出发，按折 线 DCBAD 方向以 2cm/s 的速度运动，动点 N 从点 D 出发，按折线 DABCD 方向以 1cm/s 的速 度运动． （1）若动点 M、N 同时出发，经过几秒钟两点相遇？ （2）若点 E 在线段 BC 上，BE=2cm，动点 M、N 同时出发且相遇时均停止运动，那么点 M 运动到第几秒钟时，与点 A、E、M、N 恰好能组成平行四边形？ 八年级数学期中考试参考答案 一、选择题(每小题 3 分，共 24 分) 1．B 2．A 3．B 4．C 5．D 6．D 7．C 8．C 二、填空题（每空 2 分，共 36 分） 图（1） 9．±5，-3 10．3，＞ 11．16，1/3 12．-3，-8 13．AD=BC 等 14．800，20° 15．2 16．9 17．顺，40 18．10 19. 6，2 73 20. 2 1)1(2 1  nnnn 三、解答题（40 分） 21．（1）解：原式=6+3-5 (2 分) =4 (3 分) （2）解： （x-1）3= - 8 (1 分) x-1= - 2 (2 分) x= - 1 (3 分) 22. (1)略 （2 分） （2）略 （2 分） （3）略（2 分） 23. （1） 6 ，135° （每空 1 分，共 2 分） （2） 四边形 OAA1B 是平行四边形 （1 分） 两组对边相等或一组对边平行且相等（3 分） （3）S =36 （2 分） 24.解：在 Rt△ABC 中，∠B=90° ∵AB=3，BC=4 ∴AC= 543 22  （1 分） ∵CD=12，DA=13 ∴ 222 ADCDAC  ∴∠ACD=90° (3 分) ∴S 四边形 ABCD=S△ABC+S△ACD=36 （4 分） ∴铺满这块空地共需花费 360 元 (5 分) 25.证明：（1）∵OB 平分∠ABC ∴∠1=∠2 (1 分) 又∵EF∥BC ∴∠2=∠3 （2 分） ∴OE=BE （3 分） 同理可得 OF=FC （4 分） ∴OE+OF=BE+CF ∴EF=BE+CF （6 分） (2)EF=BE-CF （2 分） 26、（1）解：（1）设 t 秒时两点相遇，则有 t+2t=24，解得 t=8． 答：经过 8 秒两点相遇． （3 分） （2）由（1）知，点 N 一直在 AD 上运动，所以当点 M 运动到 BC 边上的时候，点 A、E、M、 N 才可能组成平行四边形， 设经过 x 秒，四点可组成平行四边形．分两种情形： ①8-x=9-2x，解得 x =1，不符合题意，舍去. （2 分） ②8-x=2x-9，解得 x= 3 17 . （2 分） 八年级上册期中数学测试题 A 卷 一、选择题 1．已知 y1=x-5，y2=4x-1，使不等式 y1>y2 成立的 x 值中最大整数是（ ）． A．-2 B．-2 C．-1 D．0 2．如图 1 所示，已知 OA=OB，OC=OD，AD，BC 相交于 E，则图中全等的三角形的个数是（ ）． A．2 B．3 C．4 D．5 D A C E B O ③ ② ① D B A C (1) (2) (3) 3．如图 2 所示，某同学将一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全 一样的玻璃，那么最省事的办法是（ ）． A．带①去 B．带②去 C．带③去 D．带①②去 4．已知点（-2，y1），（-1，y2），（1，y3）都在直线 y=- 1 3 x+b 上，则 y1，y2，y3 的值的大小 关系是（ ）． A．y1>y2>y3 B．y1y1>y2 D．y3>y1>y2 5．函数 y=kx+b 的图像与函数 y=- 1 2 x+3 的图像平行，且与 y 轴的交点为 M（0，2），则其 函数表达式为（ ）． A．y= 1 2 x+3 B．y= 1 2 x+2 C．y=- 1 2 x+3 D．y=- 1 2 x+2 6．如图 3，△ABC≌△BAD，A 和 B，C 和 D 是对应顶点，如果 AB=6cm，BD=5cm，AD=4cm， 那么 BC 的长是（ ）． A．4cm B．5cm C．6cm D．无法确定 7．已知一次函数 y1=（m2-2）x+1-m 与 y2=（m2-4）x+2m+3 的图像与 y 轴交点的纵坐标互为 相反数，则 m 的值为（ ）． A．-2 B．2 C．-3 D．-4 8．若直线 y=2x+3 与 y=3x-2b 相交于 x 轴上，则 b 的值是（ ）． A．b=-3 B．b=- 3 2 C．b=- 9 4 D．b=6 二、填空题 1．已知 y-2 与 x 成正比例，当 x=3 时，y=1，那么 y 与 x 之间的函数关系式为______． 2．一个扇形统计图中，某部分所对应的扇形圆心角为 36°，则该部分所占总体的百分比是 ______． 3．已知△ABC≌△A′B′C′，A 与 A′，B 与 B′是对应顶点，△ABC 的周长为 12cm， AB=3cm，BC=4cm，则 A′B′=______cm，B′C′=______cm，A′C′=_____cm． 4．如图 4 所示，∠B=∠D=90°，要证明△ABC与△ADC全等，还需要补充的条件是 ________． D B A C 2 3 1 E D B A C y x 2 -3 0 (4) (5) (6) 5．如果点 A（m，4）在连结点 B（0，8）和点 C（-4，0）的线段上，则 m=________． 6．若一次函数 y=3x+b 经过点 A（1，7），则 b-2=_______，该函数图像经过点 B（4，______） 和点 C（_____，0）． 7．如图 5 所示，AB=AC，AD=AE，∠BAC=∠DAE，∠1=25°，∠2=30°，则∠3=_____． 8．函数 y=kx+b 的图像如图 6 所示，则当 y<0 时，x 的取值范围是________． 三、解答题 1．某车间有 20 名工人，每人每天加工甲种零件 5 个或乙种零件 4 个，在这 20 名工人中， 派 x 人加工甲种零件，其余人加工乙种零件，已知每加工一个甲种零件可获利 16 元，每 加一个乙种零件可获利 24 元． （1）写出此车间每天所获利润 y（元）与 x（人）之间的函数关系式． （2）若要使车间每天获利不低于 1800 元，问至少应派多少人加工乙种零件． 2．某校七年（1）班参加兴趣小组的人数统计图如图所示． （1）该班共有多少人参加？ （2）哪小组的人最多？哪小组的人最少？ （3）根据上面的数据做统计表． （4）由统计表做扇形统计图． 3．如图，已知 AC=AB，AE=AD，∠EAB=∠DAC，问 BD 与 EC 相等吗？说明理由． E D B A C 4．某晚报“百姓热线”一周仙接到热线电话记录为：奇闻轶事 5%，道路交通 20%，环境 保护 35%，房产纠纷 15%，建议与表扬 10%，投诉 15%． （1）请你设计一张表格，简明地表达上面的信息； （2）请你再分别将其设计成条形统计图和扇形统计图； （3）请你结合图表，通过比较说明你从中得到的观点． 5．甲、乙两人在相同条件下各射靶 10 次，每次射靶的成绩情况如下表： 1 2 3 4 5 6 7 8 9 1 0 甲击靶的环数 9 5 7 8 7 6 8 6 7 7 乙击靶的环数 2 4 6 8 7 7 8 9 9 1 0 根据上面的统计表，制作适当的统计图表示甲、乙两人的射击成绩． B 卷 1．（探究题）如图所示，∠ACB=∠ADB=90°，AC=AD，E 在 AB 上，试说明：（1）点 A在∠ CBD 的平分线上．（2）CD=DE． D A C B E 2．（与现实生活联系的应用题）如图所示，O 为码头，A，B 两个灯塔与码头的距离相等， OA，OB 为海岸线，一轮船离开码头，计划沿∠AOB 的平分线航行，在航行途中，测得 轮船与灯塔 A 和灯塔 B 的距离相等，试问轮船航行时是否偏离预定航线，请说明理由． B A 0 3．（与现实生活联系的应用题）下面两个统计图（如图所示）反映的是某市甲、乙两所中学 的学生参加课外活动的情况，请你通过图中信息回答下列问题： （1）通过对图（1）的分析，写出一条你认为正确的结论． （2）通过对图（2）的分析，写出一条你认为正确的结论． （3）2003 年甲、乙两所中学参加科技活动的学生人数共有多少？ 乙校 甲校 625 600 1000 1000 2000 年 人数 2003 2000 1997 500 1000 1500 2000 4．（图表题）宿豫区黄中对初二年级女生仰卧起坐的测试成绩进行统计分析，将数据整理 后，画出如下频数分布直方图，如图，已知图中从左到右的第一、第二、第三、第四、 第六小组的频率依次是 0.10，0.15，0.20，0.30，0.05，第五小组的频数是 36，根据所给 的图填空： （1）第五小组的频率是_______，请补全这个频数分布图． （2）参加这次测试的女生人数是______；若次数在 24（含 24 次）以上为达标（此标 准为中考体育标准），则该校初二年级女生的达标率为________． （3）请你用统计知识，以中考体育标准对宿豫区 22 所中学初二学生仰卧起坐成绩的达 标率作一个估计． 次数 频树/人数 41.5 35.5 29.5 23.5 17.5 11.5 5.5 答案 A 卷 一、1．B 解析：当 y1>y2 时，x-5>4x-1，解得 x<- 4 3 ． ∵小于- 4 3 的最大整数为-2，∴应选 B． 2．C 解析：因 OA=OB，OC=OD，∠AOB=∠AOB，可确定△OAD≌△OBC， 进而会得到相等的角、相等的边， 进而可利用三角形全等的判定方法确定△OCE≌△ODE，△ACE≌△BDE，△AOE≌△BOE． 3．C 解析：利用三角形全等的条件（ASA），带③去便能保证所配的玻璃与原来一模一样． 4．A 解析：对于 y=- 1 3 x+b 来说，k=- 1 3 <0，∴y 随 x 的增大而减小． ∵-2<-1<1，∴y1>y2>y3． 5．D 解析：∵直线 y=kx+b 与直线 y=- 1 2 x+3 平行，∴k=- 1 2 ． ∵其与 y 轴的交点为（0，2），∴b=2， ∴其表达式为 y=- 1 2 x+2．故应选 D． 6．A 解析：∵△ABC≌△BAD， ∴BC=AD=4cm． 提示：本题关键要确定对应边． 7．D 解析：根据题意得 2 2 (1 ) (2 3) 0, 2 0, 4 0, m m m m           由①得 m=-4，且能满足②，③， ∴m 的值为-4． 8．C 解析：在 y=2x+3 中，当 y>0 时， 2x+3=0，x=- 3 2 ， ∴交点坐标为（- 3 2 ，0）． 将 x=- 3 2 ，y=0 代入 y=3x-2b 得- 9 2 -2b=0，b=- 9 4 ． 二、1．解析：设 y-2=kx，把 x=3，y=1 代入，得 1-2=3k，k=- 1 3 ． ∴y-2=- 1 3 x， 即 y=- 1 3 x+2． 答案：y=- 1 3 x+2． 2．解析： 36 360   = 1 6 ． 答案： 1 6 3．解析：∵△ABC≌△A′B′C′， ∴A′B′=AB=3cm， B′C′=BC=4cm， A′C′=AC=12-（3+4）=5（cm）． 答案：3 4 5 4．AB=AD，或 BC=CD，或∠BAC=∠DAC，或∠BCA=∠DCA ① ② ③ 5．解析：设线段 BC 所在的直线为 y=kx+b，根据题意得 8, 4 0, b k b     解得 2, 8. k b    ∴y=2x+8，当 y=4 时， 4=2x+8，x=-2，即 m=-2． 答案：-2 6．解析：∵直线 y=3x+b 经过点 A（1，7）， ∴3+b=7，b=4． ∴y=3x+4，∴b-2=4-2=2． 当 x=4 时，y=3×4+4=16． ∴B（4，16）． 当 y=0 时，0=3x+4，x=- 4 3 ， ∴C（- 4 3 ，0）． 答案：2 16 - 4 3 7．55° 8．解析：由图像可以看，当 y<0（即 x 轴下方的部分）时，对应的 x 的取值范围是 x<-3． 答案：x<-3 提示：此题也可根据图中提供的信息求出函数解析式，然后再借助不等式，求出 x 的范 围． 三、1．解析：（1）根据题意得 y=16×5x+24×4（20-x），化简得 y=-16x+1920． （2）当 y≥1800 时，-16x+1920≥1800，-16x≥-120，x≥15 2 ． ∴最多派 7 人加工甲种零件． 故最少应派 13 人加工乙种零件． 2．解析：（1）6+14+12+18+10=60（人）． ∴该班共有 60 人参加兴趣小组； （2）计算机小组里有 18 人，人数最多，小提琴小组里有 6 人，人数最少； （3）作统计表如下： 组别 小提琴 围棋 书法 计算机 绘画 人数/人 6 14 12 18 10 （4）小提琴组部分圆心角为 360°× 6 60 =36°； 围棋组部分圆心角为 360°× 14 60 =84°； 书法组部分圆心角为 360°× 12 60 =72°； 计算机组部分圆心角为 360°× 18 60 =108°； 绘画组部分圆心角为 360°× 10 60 =60°； 做扇形统计图答图． 10% 16.7% 小提琴组 绘画组 计算机组 书法组 围棋组 20% 23.3% 30% 3．解析：BD 与 EC 相等． 理由：∵∠EAB=∠DAC， ∴∠EAB+∠BAC=∠DAC+∠BAC， 即∠EAC=∠DAB． 在△ABD 和△ACE 中， AB=AC，∠EAC=∠DAB，AE=AD， ∴△ABD≌△ACE（SAS）， ∴BD=EC． 4．解析：（1）根据所给数据可设计表格为： 电话 奇闻轶事 道路交通 环境保护 房产纠纷 建议与表扬 投诉 比率 5% 20% 35% 15% 10% 15% （2）①条形统计图，如答图所示． ②扇形统计图，如答图所示． （3）从统计表以及统计图可知：百姓积极关注“环保、道路交通”等热点问题，其中 关心环保的人数为最多，说明百姓环保意识强． 5．解析：如答图所示． 提示：本题可选用折线统计图，在制作折线统计图时，要仔细描点、连线，并且甲、 乙两人成绩的变化分别用虚线和实线进行描述． B 卷 1．证明：（1）在 Rt△ABC 和 Rt△ABD 中， AC=AD，AB=AB， ∴Rt△ABC≌Rt△ABH（HL） ∴∠1=∠2，∴点 A 在∠CBD 的平分线上． （2）∵Rt△ABC≌Rt△ABD， ∴BC=BD． 在△BEC 和△BED 中， BC=BD，∠1=∠2，BE=BE， ∴△BEC≌△BED（SAS）， ∴CE=DE． 2．解析：如答图所示，轮船没有偏离预定航行． 理由：假设轮船在点 P 处，由题意可知 PA=PB，连结 OP． 在△AOP 和△BOP 中， OA=OB，PA=PB，OP=OP， ∴△AOP≌△BOP， ∴∠1=∠2， ∴点 P 在∠AOB 的平分线上． 故没有偏离预定航线． 提示：先将实际问题抽象成数学问题，然后应用有关数学知识来加以说明，这是解 决实际问题的常用方法． 3．解析：（1）“1997～2003 年甲校学生参加课外活动的人数比乙校增长得快”等． （2）“甲校参加文体活动的人数比参加科技活动的人数多”等． （3）2000×38%+1000×60%=1360（人）． 所以 2003 年两所中学的学生参加科技活动的总人数是 1360 人． 4．解析：（1）第五小组的频率为： 1-0.10-0.15-0.20-0.30-0.05=0.20． 补图如答图所示． （2）参加这次测试的女生人数为 36÷0.20=180（人）． 该校初二年级女生的达标率为 （1-0.10-0.15-0.20）×100%=55%． （3）以宿豫区黄中初二女生的仰卧起坐成绩作为一个样本，可以估计宿豫区 22 所中学 初二女生的仰卧起坐成绩达标率约为 55%． 答案：（1）0.20 补图如图所示． （2）180 人 55% （3）约 55% 提示：根据频率的关系来补图，长方形的高与频率成正比． 八 年 级 数 学 试 题 题号 一 二 三 总分 17 18 19 20 21 22 23 24 得分 一、选择题(每题 3 分，共 24 分) 1. 下列图案是轴对称图形的有（ ） A．1 个 B．2 个 C．3 个 D．4 个 2．如果一个有理数的平方根和立方根相同，那么这个数是（ ） 得 分 评 卷 人 A. ±1 B. 1 C. 0 D. 0 和 1 3. 下列说法：①用一张底片冲洗出来的 2 张 1 寸相片是全等形；②所有的正五边形是全等 形；③全等形的周长相等；④面积相等的图形一定是全等形．其中正确的是（ ） A. ①②③ B．①③④ C．①③ D．③ 4．将一矩形纸片按如图方式折叠，BC、BD 为折痕，折叠后 / /A B E B与 与在同一条直线上， 则∠CBD 的度数 （ ） A. 大于 90° B. 等于 90° C. 小于 90° D. 不能确定 5. 81 的平方根是 （ ） A．9 B． 9 C．3 D． 3 6. 估计 20 的算术平方根的大小在（ ） A．2 与 3 之间 B．3 与 4 之间 C．4 与 5 之间 D． 5 与 6 之间 7. 如图 1 所示，将矩形纸片先沿虚线 AB 按箭头方向向右对折，接着将对折后的纸片沿虚 线 CD 向下对折，然后剪下一个小三角形，再将纸片打开，则打开后的展开图是（ ） C D B(A) A B A B C D 图 1 A． B． C． D． 8．如图，在△ABC 中，AB=AC，∠A=36°，BD、CE 分别是 △ABC、△BCD 的角平分线， 则图中的等腰三角形有 （ ） A．5 个 B． 4 个 A EB D C A E C．3 个 D． 2 个 二、填空题（每题 4 分，共 32 分) 9. 无理数 3 的相反数是_______，绝对值是___________. 10. 在 -3，－ 3 ， －1， 0 这四个实数中，最大的是________,最小的是___________. 11. 以下是一个简单的数值运算程序： 当输入 x 的值为 4 时，则输出的结果为___________. 12. 已知等腰三角形的一个内角为 70°，则另外两个内角的度数是___________ . 13. 如图,△ABD≌△ACE,则 AB 的对应边是_________,∠BAD 的对应角是______. 14. 如图，AD∥BC, ∠ABC 的平分线 BP 与∠BAD 的平分线 AP 相交于点 P，作 PE⊥AB 于点 E.若 PE=2，则两平行线 AD 与 BC 间的距离为___________. （第 13 题图） （第 14 题图） 15．如图，点 P 在∠AOB 的内部，点 M、N 分别是点 P 关于直线 OA、OB的对称点，线段 MN 交 OA、OB 于点 E、F，若△PEF 的周长是 20cm，则线段 MN 的长是___________． 16. 如图所示， 90E F     ， B C   ， AE AF ，结论：① EM FN ；② CD DN ；③ FAN EAM   ；④ ACN ABM△ ≌△ ．其中正确的有__________. B P E A D C 得 分 评 卷 人 输人 x 平方 － 8 开立方 输出结果 （第 15 题图） （ 第 16 题图） 三、解答题（共 56 分） 17. 计算（每小题 5 分，共 10 分） （1） 31 0.81 8 496    （2） 21 12 2 ( 16) ( )8 2       18.（6 分）自由下落的物体的高度 h（m）与下落时间 t（s）的关系为 h＝4.9t2．有一学生 不慎让一个玻璃杯从 19.6m 高的楼上自由下落，刚好另一学生站在与下落的玻璃杯同一直 线的地面上，在玻璃杯下落的同时楼上的学生惊叫一声，这时楼下的学生能躲开吗（声音 的速度为 340m/s）？ 19.（6 分）已知：如图，D 是△ABC 的边 AB 上一点, DF 交 AC 于点 E, DE=FE, FC∥AB. 求证：AD=CF． 得 分 评 卷 人 E A B D F C 20. （6 分）如图,写出 A、B、C 关于 y 轴对称的点坐标,并作出与△ABC 关于 x 轴对称的图 形. 21. (8 分) 认真观察下图 4 个图中阴影部分构成的图案，回答下列问题： （1）请写出这四个图案都具有的两个共同特征． 特征 1：_________________________________________________； 特征 2：_________________________________________________． （2）请在下图中设计出你心中最美丽的图案，使它也具备你所写出的上述特征 22．(8 分) 如图，两条公路 AB，AC 相交于点 A，现要建个车站 D，使得 D 到 A 村和 B 村的 距离相等，并且到公路 AB、AC 的距离也相等. (1) 请在图 1 中画出车站的位置． (2) 若将 A、B 抽象为两个点，公路 AC 抽象为一条直线，请在直线 AC 上找一个点 M，使△ ABM 是等腰三角形，这样的点能找几个？请你找出所有符合条件的点． 图 1 图 2 23.（10 分）在△ABC 中,AB=CB,∠ABC=90º,F 为 AB 延长线上一点,点 E 在 BC 上,且 AE=CF. (1)求证:Rt△ABE≌Rt△CBF; (2)若∠CAE=30º,求∠ACF 度数. AB C E F B C A A B C 24．（10 分）数学课上，李老师出示了如下框中的题目. 小敏与同桌小聪讨论后，进行了如下解答： （1）特殊情况，探索结论 当点 E 为 AB 的中点时，如图 1，确定线段 AE 与 DB 的大小关系，请你直接写出结论： AE DB （填“>”,“<”或“=”）. （2）特例启发，解答题目 解：题目中， AE 与 DB 的大小关系是： AE DB（填“>”,“<”或“=”）.理由如下：如图 2， 过点 E 作 / /EF BC ，交 AC 于点 F . （请你完成以下解答过程） F 第 26 题图 1 第 26 题图 2 （3）拓展结论，设计新题 在等边三角形 ABC 中，点 E 在直线 AB 上，点 D 在直线 BC 上，且 ED EC .若 ABC 的边长为 1， 2AE  ，求CD 的长（请你直接写出结果）. 一、选择题（24 分） 1. B 2. C 3. C 4. B 5. D 6. C 7. D 8. A 二、填空题（32 分） 9. 3,3 ; 10. 0, -3； 11. 2 ; 12. 70°40°或 55°55°；13. AC ,∠CAE ； 14. 4 ; 15. 20cm； 16.①③④. 三、解答题（64 分） 17.(10 分) （1）原式= 7)2(9.06 1  …………………………2 分 = 7210 9 6 1  ……………………………4 分 = 20 39 …………………………………5 分 (2) 原式= )2(164 222  …………………2 分 = 324 222  ……………………………4 分 = 24 334  ………………………………… 5 分 18. （6 分）解：根据题意得 6.199.4 2 t …………………1 分 9.4 6.192 t …………………2 分 AB C E F 2t …………………3 分 声音传播所用的时间是 )(6.03406.19 s …………………4 分 因为 6.0 ＜ 2 …………………………………5 分 答：楼下的学生能躲开。…………………………………6 分 19．（6 分）证明（1）∵CF∥AB ∴ ∠ADE=∠F …………………1 分 在△ADE 和△CFE 中 ∠ADE=∠F DE=FE ∠AED=∠CEF ∴△ADE≌△CFE ………………………………5 分 ∴AD=CF ………………………………6 分 20.(6 分) A、B、C 关于 y 轴对称的点坐标分别为（4，1）（1，-1）（3，2） 每点 1 分，共 3 分 图略（3 分） 21. （8 分）解：（1）特征 1：都是轴对称图形；…………………2 分 特征 2：这些图形的面积都等于 4 个单位面积； …………………2 分 （2）满足条件的图形有很多，只要画正确一个，都可以得满分．…………………4 分 22. （8 分）（1）∠BAC 的平分线与线段 AB 的中垂线的交点即为车站位置（图略）………4 分 （2）符合条件的点共有 4 个。每找对一个得 1 分，共 4 分。 23. （10 分）（1）∵∠ABC=90°,∴∠CBF=∠ABE=90°. 在 Rt△ABE 和 Rt△CBF 中, ∵AE=CF, AB=BC, ∴Rt△ABE≌Rt△CBF(HL) …………5 分 (2)∵AB=BC, ∠ABC=90°, ∴ ∠CAB=∠ACB=45°. E A B D F C ∵∠BAE=∠CAB-∠CAE=45°-30°=15°. …………7 分 由（1）知 Rt△ABE≌Rt△CBF， ∴∠BCF=∠BAE=15°, …………8 分 ∴∠ACF=∠BCF+∠ACB=45°+15°=60°. …………10 分 24.(10 分) (1) = ………………2 分 (2) = ………………2 分 证明：在等边△ABC 中，∠ABC=∠ACB=∠BAC=60°，AB=BC=AC， ∵EF∥BC，∴∠AEF=∠AFE=60°=∠BAC， ∴AE=AF=EF， ∴AB﹣AE=AC﹣AF， 即 BE=CF， ∵∠ABC=∠EDB+∠BED=60°， ∠ACB=∠ECB+∠FCE=60°， ∵ED=EC， ∴∠EDB=∠ECB， ∴∠BED=∠FCE， ∴△DBE≌△EFC， ∴DB=EF， ∴AE=BD． …………………7 分 （3）答：CD 的长是 1 或 3．…………………3 分 八年级上册数学期中考试卷 一、选择题(共 10 小题，每小题 3 分，共 30 分。请将你认为正确答 案前面的代号填入括号内） 1．如图所示，图中不是轴对称图形的是（ ） A B C D 2.下列图形具有稳定性的是（ ） A. 正方形 B. 长方形 C. 直角三角形 D. 平行四边形 3.以下列各组线段为边，能组成三角形的是（ ） A. 2 cm ，3 cm，5 cm B. 3 cm，3 cm，6 cm 班 级 姓 名 座 位 号 … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … E 第 13 题 图图 C. 5 cm，8 cm，2 cm D. 4 cm，5 cm，6 cm 4.点 M（—1，2）关于 y 轴对称的点的坐标为（ ） A.（－1，－2） B.（1，2） C.（1，－2） D.（2，－1） 5、十二边形的外角和是 ( ) A. 180° B. 360° C.1800 ° D2160° 6.已知等腰三角形的两边长分别为 3 和 6，则它的周长等于（ ） A. 12 B. 12 或 15 C. 15 D. 15 或 18 7．下列条件中，能判定△ABC≌△DEF 的是（ ） A ． ∠A=∠D，∠B=∠E，∠C=∠F B ． AC=DF，∠B=∠E，BC=EF C ． AB=DE，∠B=∠E，AC=DF D ． AB=DE，∠B=∠E，BC=EF 8．已知点 M（a，3），点 N（2，b）关于 y 轴对称，则（a+b）2013 的值（ ） A． ﹣3 B． ﹣1 C． 1 D． 3 9、以下说法正确的是 （ ） ①有两个角和其中一个角的对边对应相等的两个三角形全等； ②有一边和一个角对应相等的两个三角形全等； ③有一边相等的两个等边三角形全等； ④一个锐角和一条对应边相等的两个直角三角形全等。 A、①②③ B、①②④ C、①③④ D、②③④ 10、如图，BE、CF 是△ABC 的角平分线，∠ABC=80°， ∠ACB=60°，BE、CF 相交于 D，则∠CDE 的度数是（ ） A、110° B、70° C、80° D、75° 第 12 题 第 10 题 C D B A 第 11 题 二、填空题（每题 4 分，共 24 分） 11、如图，一面小红旗其中∠A=60°, ∠B=30°,则∠BCD= 。 12、为了使一扇旧木门不变形，木工师傅在木门的背面加钉了一根木条这样做 的道理是___________________. 13、如图所示，∠1=∠2，∠C=90°，若DC=6，AC=8则D到AB的距离DE= 。 14、如14 题图，△ABC≌△EDF，DF＝BC，AB＝ED，EF＝15，EC＝10，则AE 的长是 。 15、六边形有 条对角线。 16．如图，已知 AD 平分∠BAC，要使 △ ABD≌△ACD， 根据“AAS”需要添加条件 _________ ． 四、解答题（共 46 分） 17、（5 分）如图，画出 △ ABC 关于直线 m 对称的 △ A′B′C′ 图1 A F B D C E B A C D 第 16 题 第 14 题 … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … D A E C B A B C m 18、（6 分）如图，某地有两所大学和两条交叉的公路．图中点 M，N 表示大学， OA，OB 表示公路，现计划修建一座物资仓库，希望仓库到两所大学的距离相同， 到两条公路的距离也相同，你能确定出仓库 P 应该建在什么位置吗？请在图中 画出你的设计．（尺规作图，不写作法，保留作图痕迹） 19、(6 分)如图,△ABC 中,BD 是∠ABC 的角平分线,DE∥BC,交 AB 于 E, ∠ABC=60° ,求△BDE 各内角的度数. 20、(7 分)如图，为了测量一池塘的宽 AB，在岸边找到一点 C，连接 AC， 在 AC 的延长线上找一点 D，使得 DC=AC，连接 BC，在 BC 的延长线上找 一点 E， 使 得 EC=BC， 测 出 DE=60m， 试 问 池 塘 的 宽 AB 为 多 少 ？ 请 说 明 理由． 21. (7 分)如图，在△ABC 中，DE 是 AC 的垂直平分线，AE=4cm, △ABD 的周长 为 15cm,求△ABC 的周长。 22．（7 分）如图，点 E、F 在 BC 上，BE=FC，AB=DC，∠B=∠C． 求证：∠A=∠D． 23．（8 分）如图，在 △ ABC 中，AB=AC，BD⊥AC 于 D，CE⊥AB 于 E，BD、 CE 相交于 F． 求证：AF 平分∠BAC． E F D A A B D C E