浙教版八年级上册数学同步课件-第2章-2探索勾股定理 19页

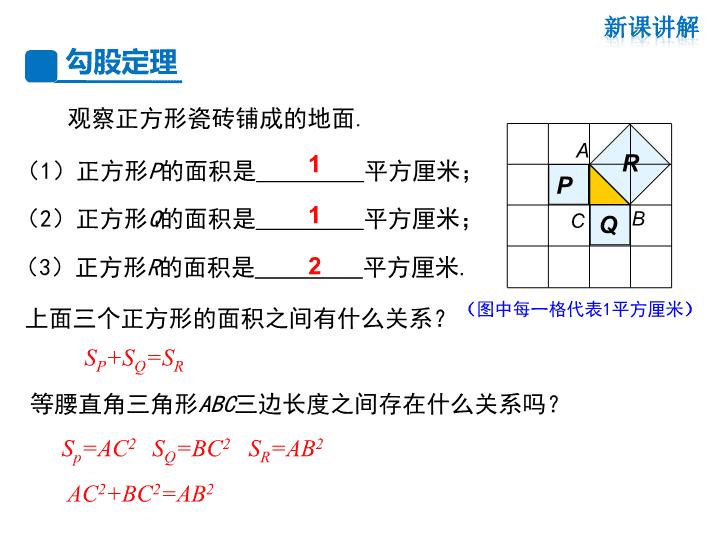
第2章 特殊三角形 2.7 探索勾股定理 第1课时 勾股定理 某楼房三楼失火，消防队员赶来救火，了解到每层楼 高3米，消防队员取来6.5米长的云梯,如果梯子的底部离 墙基的距离是2.5米,请问消防队员能否进入三楼灭火? 情境引入 （图中每一格代表1平方厘米） （1）正方形P的面积是 平方厘米； （2）正方形Q的面积是 平方厘米； （3）正方形R的面积是 平方厘米. 1 2 1 SP+SQ=SR R Q P A C B AC2+BC2=AB2 等腰直角三角形ABC三边长度之间存在什么关系吗？ Sp=AC2 SQ=BC2 SR=AB2 上面三个正方形的面积之间有什么关系？ 观察正方形瓷砖铺成的地面. 勾股定理 这说明在等腰直角三角形ABC中,两直角边的平 方和等于斜边的平方. 那么,在一般的直角三角形中,两直角边的平方和 是否等于斜边的平方呢? 想一想 探究发现 P的面 积(单 位长度) Q的面 积(单 位长度) R的面 积(单 位长度) 图2 图3 P、Q、 R面积 关系 直角三 角形三 边关系 Q P R Q P R A BC A BC 9 16 25 9 4 13 SP+SQ=SR (每一小方格表示1平方厘米) BC2+AC2=AB2 试一试 图2 图3 Q P R Q P R 把R看作是四个直角三角形的面积+小正方形面积. Q P R Q P R 把R看作是大正方形面积减去四个直角三角形的面积. 432 147 2  25 S正方形R 分别以5cm、12cm为直角三角形的直角边作出一个 直角三角形ABC，测量斜边的长度，然后验证上述关系 对这个直角三角形是否成立. 做一做 关系成立 由前面的探索可以发现：对于任意的直角三角形，如 果它的两条直角边分别为a、b，斜边为c，那么一定有 a2+b2=c2. 勾股定理:直角三角形两直角边的平方和等于斜边的平方. 几何语言： ∵在Rt△ABC中 ，∠C=90°， ∴a2+b2=c2（勾股定理）. a A B C b c ∟ 勾股定理揭示了直角三角形三边之间的关系. 归纳总结 温馨提示：上述这种验证勾股定理的方法是用面积法 “赵爽弦图”表现了我国古人对数学的钻研精神和聪明 才智，它是我国古代数学的骄傲.因为，这个图案被选为2002 年在北京召开的国际数学大会的会徽. a bc S大正方形＝c2， S大正方形＝4·S三角形＋S小正方形， 赵爽弦图 证明： b-a a a a a b b b b c cc c 方法小结：我们利用拼图的方法，将形的问题与数的问题结 合起来，再进行整式运算，从理论上验证了勾股定理． 大正方形的面积可以表示为 ; 也可以表示为 . (a+b)2 c2 +4•ab/2 ∵ (a+b)2 = c2 + 4•ab/2， a2+2ab+b2 = c2 +2ab， ∴ a2+b2=c2. 用四个全等的直角三角形，还可以拼成如图所示的图形， 你能否根据这一图形，证明勾股定理. 做一做 求下列图形中未知正方形的面积或未知边的长度（口答）： ? 225 100 x 15 17 已知直角三角形两边，求第三边. 练一练 1.图中阴影部分是一个正方形，则此正方形的面积 为 . 15 cm 17 cm 64 cm² 2.在△ABC中, ∠C=90°,AC=6,CB=8,则△ABC面积为_____, 斜边为上的高为______.   24 4.8 A BC D 3.判断题. （1）△ABC的两边AB=5,AC=12,则BC=13. ( ) （2）△ABC的a=6,b=8,则c=10. ( ) 4.一高为2.5米的木梯,架在高为2.4米的墙上(如图), 这时梯脚与墙的距离是多少? A BC 解：在Rt△ABC中，根据勾 股定理，得 BC2=AB2-AC2 =2.52-2.42 =0.49， 所以BC=0.7. 5.飞机在空中水平飞行，某一时刻刚好飞到一个男孩头 顶上方4 km处，过了15 s，飞机距离这个男孩头顶5 km. 这一过程中飞机飞过的距离是多少千米？ 4 5 5 4 C B A 解：在Rt△ABC中， 即飞机飞过的距离是3km. 2 2 2=5 -4 =9 >0 =3(km). BC BC BC  ， ， 6.如图,一根旗杆在离地面9 m处折断,旗杆顶部落在离 旗杆底部12 m处.旗杆原来有多高? 12 m 9 m 解：设旗杆顶部到折断处的距离为x m. 根据勾股定理，得 x=15, 15+9=24. 即旗杆原来高24 m. 2 2 29 12 x  ， 勾股 定理 如果直角三角形两直角边长 分别为a、b，斜边长为 c ， 那么a2+b2=c2 利用勾股定理进行计算