华师版数学八年级下册同步课件-第16章 分式-16分式的运算 29页

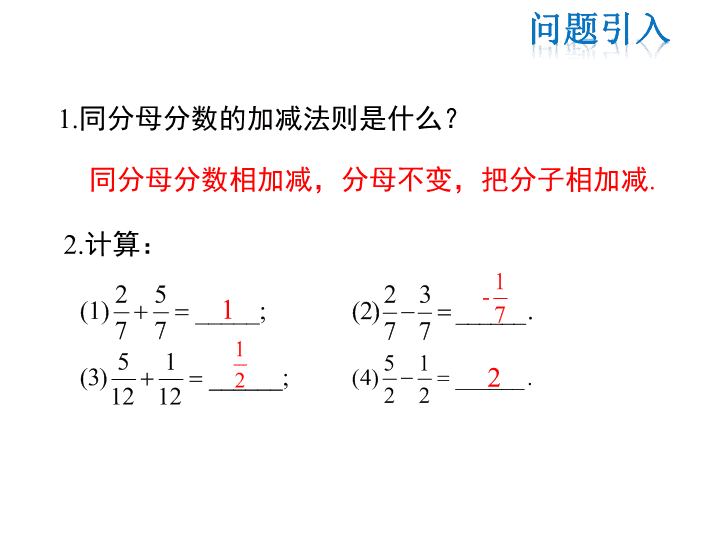
第16章 分 式 16.2 分式的运算 2 分式的加减 　1.同分母分数的加减法则是什么？ 2.计算： 2 5(1) _____; 7 7   2 3(2) ______. 7 7  1 1- 7 5 1(3) ______; 12 12   5 1(4) ______ . 2 2   2 1 2 同分母分数相加减，分母不变，把分子相加减. 类比前面同分母分数的加减，想想下面的式子 怎么计算？ xxx 132  x y x y x y  32 11 3 1 2   x y x y x y a 1 a 2+ 思考 同分母的分式应该如何加减？猜一猜 同分母分式的加减 1 2 1 2 3 5 5 5 5     1 2 1 2 1 5 5 5 5      1 2 ? a a   1 2 a  1 2 ? 2 2x x     1 2 2x   2 ? 1 1 a x x     2 1 a x   1 同分母分式相加减，分母不变，分子相加减. 上述法则可用式子表示为 b c b c a a a   2 2( ) ( ) .x y x y xy xy    计算： 解：原式 2 2 2 2( 2 ) ( 2 )x xy y x xy y xy       4xy xy  =4. 注意：结果要 化为最简分式！ 例1  x c x y x m)1(  y c y a y m)2(  cab d bca n abc m 222 )3(     yx b yx a)4( m y c x   m a c y    2 m n d a b c   a b x y   做一做 2 2 2 2 5 3 2(1) x y x x y x y     ； 解：原式= 2 2 (5 3 ) 2x y x x y    = = 注意：结果要 化为最简分式！= 2 2 3 3x y x y   3( ) ( )( ) x y x y x y    3 . x y 计算： 例2 2 2 2 2 2 2 5 3 3 5 8(2) .a b a b a b ab ab ab      解：原式= 2 2 2 2 (5 3) (3 5) (8 )a b a b a b ab      = 2 2 2 2 5 3 3 5 8a b a b a b ab      = 2 2 a b ab 注意：结果要 化为最简分式！= .a b   2 2 2 2 x x x x       ?2 4 2)1( 2     xx x ?1 3 1 1 1 2)2(        x x x x x x 2 4 2 x x        2 1 3 1 x x x x       2 1 3 1 x x x x        1 x x   做一做 异分母分式的加减 请计算 ( )， ( ).  3 1 2 1  3 1 2 1 3 1 2 1  6 23  6 5  5 6 1 6 6 2 6 3  3 1 2 1  6 2 6 3  6 23  6 1  异分母分数相加减 分数的通分 依据：分数的基本性质 转化 同分母分数相加减 异分母分数相加减，先通分， 变为同分母的分数，再加减 . 2 问题 3 1 2 1  6 23  6 5  6 2 6 3  3 1 2 1  依据:分数基本性质 分数的通分 同分母分数相加减 异分母分数相加减 转化 异分母分数相加减，先通分， 变为同分母的分数，再加减. 6 2 6 3  6 23  6 1  db 11  bd b bd d  bd bd   db 11  bd b bd d  bd bd   异分母分式相加减 分式的通分 依据:分式基本性质 转化 同分母分式相加减 异分母分式相加减，先通分， 变为同分母的分式，再加减. d b bd  d b bd  请思考： （ ）， （ ）. 1 1 b d   1 1 b d   异分母分式相加减，先通分，变为同分母的分 式，然后再加减. 上述法则可用式子表示为 a c ad bc ad bc b d bd bd bd      2 1 1 1 x x x     （1） ； 解：原式= 2 1 1 1 x x x     = = 注意：(1-x)=-(x-1) 2 ( 1) 1 x x    3 . 1 x x   计算： 分母不同，先 化为同分母. 例3 （2） 2 3 24 ; 4 16x x    3 24 4 ( 4)( 4)x x x      3( 4) 24 ( 4)( 4) x x x      3 . 4x   （2）原式 1 1 2 3 2 3p q p q    （3） ； 解：原式= 2 3 2 3 (2 3 )(2 3 ) (2 3 )(2 3 ) p q p q p q p q p q p q        (2 3 ) (2 3 ) (2 3 )(2 3 ) p q p q p q p q       4 (2 3 )(2 3 ) p p q p q    2 2 4 . 4 9 p p q   先找出最简公分母， 再正确通分，转化为 同分母的分式相加减. 2 2 2 1 . 2 4 4 x x x x x x       （4） 解：原式= 2 2 1 ( 2) ( 2) x x x x x      = = 注意：分母是多 项式先分解因式. 2 2 ( 2)( 2) ( 1) ( 2) ( 2) x x x x x x x x       2 2 2 4 ( 2) x x x x x     先找出最简公分母， 再正确通分，转化 为同分母的分式相 加减. = 2 4 . ( 2) x x x   通分 转化为 异分母 相加减 同分母 相加减 分子（整式） 相加减 分母不变 转化为 计算： 2 1. 1 a a a    解：方法一： 原式= 2 ( 1)( 1) 1 1 a a a a a       2 2( 1) 1 a a a     2 2 1 1 a a a     1 . 1a   方法二： 原式= 2 ( 1) 1 a a a    2 ( 1) 1 1 1 1 a a a a a a a        2 2( ) ( 1) 1 a a a a a       2 2 1 1 a a a a a       1 . 1a   2 ( 1) ( 1) 1 a a a a a       把整式看成分母 为“1”的分式. 例4 阅读下面的计算过程，再完成填空. ① =　　　　　　　 　　　　② = ③ = ④ （1）上述计算过程，从哪一步开始错误，请写出该步的 代号_______； （2）错误原因___________； （3）本题的正确结果为： .        2 2 13 2 3 1 1 1 1 1 1 xx x x x x x x x             3 2 1x x   3 2 2x x   1x  ② 漏掉了分母 做一做 计算： 2 2 1 . 9 3 m m m            2 3 3 3 3 3 m m m m m m            2 3 3 3 m m m m      （ ） 解：原式 从1、-3、3中任选一个 合适的m值代入求值. 当m=1时，原式     3 3 3 m m m     1 . -3m  1 1-3  1 . 2   ∵m2-9≠0， ∴m≠+3和-3. 例5 先化简，再求值： ,其中 ．2 1 2 1 1x x    2x   解： 　 2 1 2 1 1 1 2 ( 1)( 1) ( 1)( 1) 1 ( 1)( 1) 1 . 1 x x x x x x x x x x x                 12 = 1. 2 1 x       当 时，原式 做一做 已知下面一列等式： (1)请你从这些等式的结构特征写出它的一般 性等式； (2)验证一下你写出的等式是否成立； (3)利用等式计算： 1 1 1 1 1 11 =1 = - 2 2 2 3 2 3 1 1 1 1 1 1 1 1= - = - 3 4 3 4 4 5 4 5       ； ； ； ；            1 1 1 1 . 1 1 2 2 3 3 4x x x x x x x x           例6 分析：(1)观察已知的四个等式，发现等式的左边 是两个分数之积，这两个分数的分子都是1， 后面一个分数的分母比前面一个分数的分母 大1，并且第一个分数的分母与等式的序号相 等，等式的右边是这两个分数之差，据此可 写出一般性等式； (2)根据分式的运算法则即可验证； (3)根据(1)中的结论求解． 1 1 1 1 1 1 1 1 1 1 1 1 1 11 =1 = - = - = - 2 2 2 3 2 3 3 4 3 4 4 5 4 5      ； ； ； ；             2 1 1 1 11 . 1 1 1 1 1 1 1 12 , 1 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 13 = 1 1 2 2 3 1 1 1 1 4 . 3 4 4 4 n n n n n n n n n n n n n n n n n n n n x x x x x x x x x x x x                                                            解： 原式 A. B． C．－1 D．2 1 1 1 a a a    1 1 a a   1 a a  1. 计算 的结果为（ )C 2.填空： 3 5(1) ; xy xy   4 4(2) .x y x y y x     8 xy 4 3.计算:     2 1 21 ; 2 . 3 2 1 1 b a a b a a     解：(1)原式= (2)原式= 2 2 2 22 3 2 3 . 6 6 6 b a b a ab ab ab    2 1 2 1 1a a       1 2 1 1 1a a a            1 2 1 1 1 1 a a a a a           2 3 3 . 1 1 1 a a a a a        4.先化简，再求值：： ，其中x＝2016. 3 1=2016 = . 2019 673 x 当 时，原式              3 33 18= 3 3 3 3 3 3 3 3 . 3 3 3 x x x x x x x x x x               式解 原： 分式加 减运算 加减法运算 注 意 (1)分式的分子和分母是多项式时， 在进行运算时要适时添加括号 异分母分式相加减，转化 为同分母分式的加减运算 (2)整式和分式之间进行加减运算 时，要把整式看成分母是1的分 式，以便通分 (3)异分母分式进行加减运算需要 先通分，关键是确定最简公分母