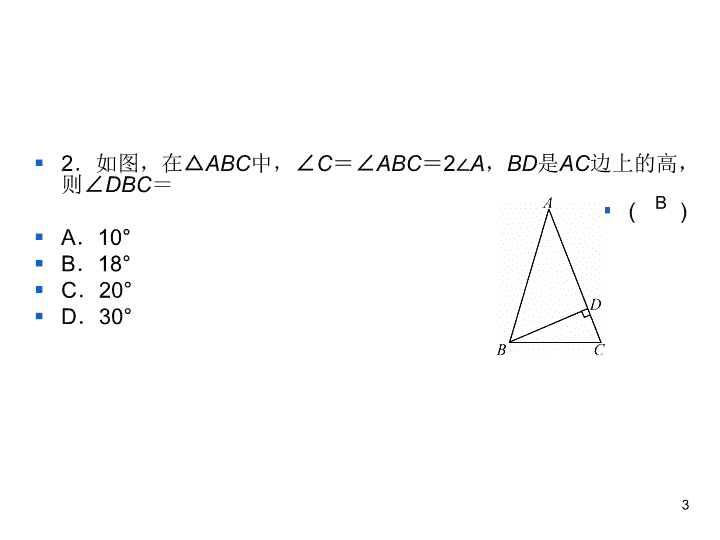人教版八年级上册数学同步练习课件-第11章-专项训练1与三角形有关角的计算 16页

第十一章　三角形 专项训练一　与三角形有关角的计算 § 类型1　与高(垂线)有关的计算 § 1．如图，在△ABC中，AD是BC边上的高， BE平分∠ABC交AC于点E，∠BAC＝60°， ∠ABE＝25°，则∠DAC的大小是(　　) § A．15°　　 § B．20°　　 § C．25°　　 § D．30° 2 重难突破 B 　 § 2．如图，在△ABC中，∠C＝∠ABC＝2∠A，BD是AC边上的高， 则∠DBC＝ § (　　) § A．10°　　 § B．18°　　 § C．20°　　 § D．30° 3 B 　 § 3．如图，已知D为△ABC的边BC延长线上 一点，DF⊥AB交AB于点F，交AC于点E， ∠A＝30°，∠D＝40°，求∠ACD的度 数． § 解：∵DF⊥AB，∴∠AFD＝90°.∵∠A＝ 30°，∴∠AEF＝180°－90°－30°＝ 60°，∴∠CED＝60°.∵∠D＝40°，∴在 △CDE中，∠ACD＝180°－40°－60°＝ 80°. 4 § 4．如图，在△ABC中，∠ACB ＝60°，∠BAC＝75°， AD⊥BC于D，BE⊥AC于E， AD交BE于H，求∠CHD的度 数． § 解：延长CH交AB于点F.由三角 形的三条高交于一点可知，CF 为△ABC的高．∵∠BAC＝ 75°，CF⊥AB，∴∠ACF＝ 90°－75°＝15°.∵∠ACB＝ 60°，∴∠DCH＝60°－15° ＝45°.∵AD⊥BC，∴在 △CDH中，∠CHD＝90°－ 45°＝45°. 5 § 类型2　与角平分线有关的计算 § 5．如图，∠A＝120°，且∠1＝∠2＝∠3， ∠4＝∠5＝∠6，则∠BDC＝ § (　　) § A．120°　　 § B．60° § C．140°　　 § D．无法确定 6 C 　 § 6．如图，BP是△ABC中∠ABC的平分线， CP是∠ACB的外角的平分线，若∠ABP＝ 20°，∠ACP＝50°，则∠P＝ __________°. 7 30　 § 7．如图，BF是∠ABD的平分线， CE是∠ACD的平分线，BF与 CE交于G，若∠BDC＝140°， ∠BGC＝110°，求∠A的度 数． § 解：连接BC.∵∠BDC＝140°， ∴∠DBC＋∠DCB＝180°－ 140°＝40°.∵∠BGC＝110°， ∴∠GBC＋∠GCB＝180°－ 110°＝70°，∴∠GBD＋ ∠GCD＝70°－40°＝ 30°.∵BF是∠ABD的平分线， CE是∠ACD的平分线， ∴∠ABD＋∠ACD＝2(∠GBD ＋∠GCD)＝60°，∴∠ABC＋ ∠ACB＝60°＋40°＝100°， ∴∠A＝180°－100°＝80°. 8 § 8．如图所示，BO、CO分别是△ABC的外角 平分线． § (1)若∠ABC＝40°，∠ACB＝60°，求 ∠BOC的度数； § (2)若∠A＝60°，求∠BOC的度数； § (3)直接写出∠BOC与∠A之间的数量关系． 9 10 § 类型3　与平行线有关的计算 § 9．如图，AB∥CD，BE⊥EF于点E，若∠B ＝25°，则∠EFD的度数是 § (　　) § A．80°　　 § B．65°　　 § C．45°　　 § D．30° 11 B § 10．如图，已知点D、E、F、G是△ABC三 边AB、BC、AC上的点，CD∥EF，且∠1＝ ∠2.若∠A＝60°，∠ADG＝52°，则 ∠ACB的度数为___________. 12 68°　 § 11．如图，已知EF∥OC，AC和BD相交于点O，∠1＝∠A＝ 65°，∠B＝30°，求∠OFE的度数． § 解：∵EF∥OC，∴∠1＝∠C.∵∠1＝∠A，∴∠A＝∠C， ∴AB∥CD，∴∠B＝∠D.∵∠1＝65°，∠B＝30°，∴∠OFE ＝∠D＋∠1＝30°＋65°＝95°. 13 § 类型4　与三角形外角有关的计算 § 12．如图所示，∠A＋∠B＋∠C＋∠D＋∠E ＝____________. § 解析：延长AE交BC于点F.∵∠A＋∠B＝ ∠AFC，∴∠AFC＋∠C＝∠AOC.∵∠D＋ ∠E＝∠AOD，∴∠A＋∠B＋∠C＋∠D＋ ∠E＝∠AOC＋∠AOD＝180°. 14 180°　 § 13．如图，已知在△ABO中， ∠AOB＝72°，∠OAB的平分线与 ∠OBA的外角∠ABN的平分线所在 直线交于点D，则∠D的大小为 ___________. 15 36°　 § 14．如图，AB∥EF，AD平分 ∠BAC，∠C＝45°，∠CDE＝ 125°，求∠ADF的度数． 16