2020八年级数学下册 专题突破讲练 函数中的动点问题试题 （新版）青岛版 12页

函数中的动点问题 ‎1. 点在线段上运动：‎ 根据线段长或图形面积求函数关系。如：如图所示，点P在线段BC、CD、DA上运动，△ABP的面积变化情况的图象是什么样的？‎ 解析：看清横轴和纵轴表示的量。‎ 答案：‎ ‎2. 双动点变化：‎ 两动点同时运动，分析图形面积变化图象。如图1，在矩形ABCD中，点E是对角线AC的三等分点（靠近点A），动点F从点C出发沿C→A→B运动，当点F与点B重合时停止运动。设点F运动的路程为x，△BEF的面积为y，那么图2能表示y与x函数关系的大致图象吗？‎ ‎ ‎ 图1 图2‎ 解析：动点问题的函数图象，解决本题应首先看清横轴和纵轴表示的量，然后根据动点的行程判断y的变化情况。‎ 答案：能。‎ ‎3. 图形运动变化所形成的函数问题：‎ 图形整体运动时，形成的函数问题；如图，边长为1和2的两个正方形，其一边在同一水平线上，小正方形自左向右匀速穿过大正方形，设穿过的时间为t，阴影部分面积为S，那么S与t的函数图象大致是什么？‎ 解析：图形运动变化所形成的函数问题．关键是理解图形运动过程中的几个分界点。‎ 12‎ 答案：‎ ‎4. 实际问题中的运动变化图象 如图，小亮在操场上玩，一段时间内沿M→A→B→M的路径匀速散步，能近似刻画小亮到出发点M的距离y与时间x之间关系的函数图象是（　　）‎ 解析：解决实际问题中的运动变化图象，要根据几何图形和图形上的数据分析得出所对应的函数的类型和所需要的条件，结合实际意义选出正确的图象。‎ 答案：‎ 总结：研究在不同位置时点的运动变化所产生的线段、面积的变化关系是重点。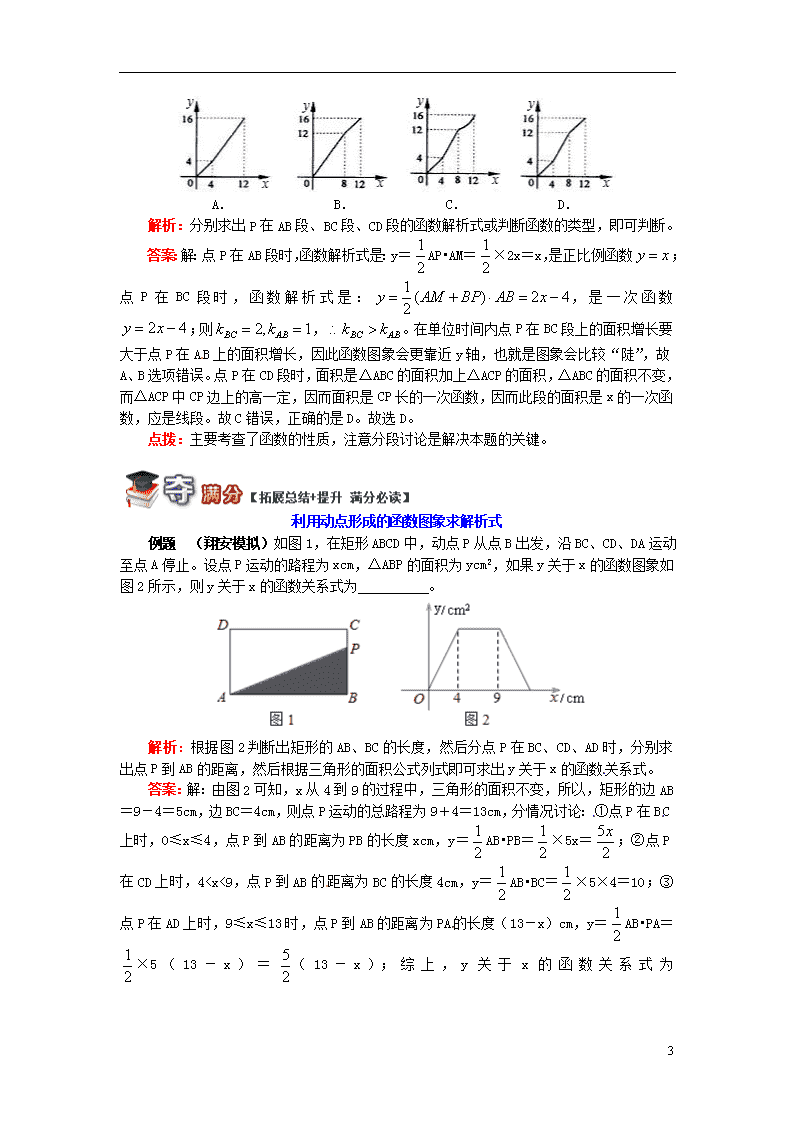‎ 例题 如图，M是边长为4的正方形AD边的中点，动点P自A点起，由A⇒B⇒C⇒D匀速运动，直线MP扫过正方形所形成面积为y，点P运动的路程为x，则表示y与x的函数关系的图象为（　　）‎ 12‎ ‎ ‎ ‎ A. B. C. D.‎ 解析：分别求出P在AB段、BC段、CD段的函数解析式或判断函数的类型，即可判断。‎ 答案：解：点P在AB段时，函数解析式是：y＝AP•AM＝×2x＝x，是正比例函数；点P在BC段时，函数解析式是：，是一次函数；则，。在单位时间内点P在BC段上的面积增长要大于点P在AB上的面积增长，因此函数图象会更靠近y轴，也就是图象会比较“陡”，故A、B选项错误。点P在CD段时，面积是△ABC的面积加上△ACP的面积，△ABC的面积不变，而△ACP中CP边上的高一定，因而面积是CP长的一次函数，因而此段的面积是x的一次函数，应是线段。故C错误，正确的是D。故选D。‎ 点拨：主要考查了函数的性质，注意分段讨论是解决本题的关键。‎ 利用动点形成的函数图象求解析式 例题 （翔安模拟）如图1，在矩形ABCD中，动点P从点B出发，沿BC、CD、DA运动至点A停止。设点P运动的路程为xcm，△ABP的面积为ycm2，如果y关于x的函数图象如图2所示，则y关于x的函数关系式为　　　　　。‎ 解析：根据图2判断出矩形的AB、BC的长度，然后分点P在BC、CD、AD时，分别求出点P到AB的距离，然后根据三角形的面积公式列式即可求出y关于x的函数关系式。‎ 答案：解：由图2可知，x从4到9的过程中，三角形的面积不变，所以，矩形的边AB＝9－4＝‎5cm，边BC＝‎4cm，则点P运动的总路程为9＋4＝‎13cm，分情况讨论：①点P在BC上时，0≤x≤4，点P到AB的距离为PB的长度xcm，y＝AB•PB＝×5x＝；②点P在CD上时，4