8年级数学教案第6讲：阶段复习与检测 10页

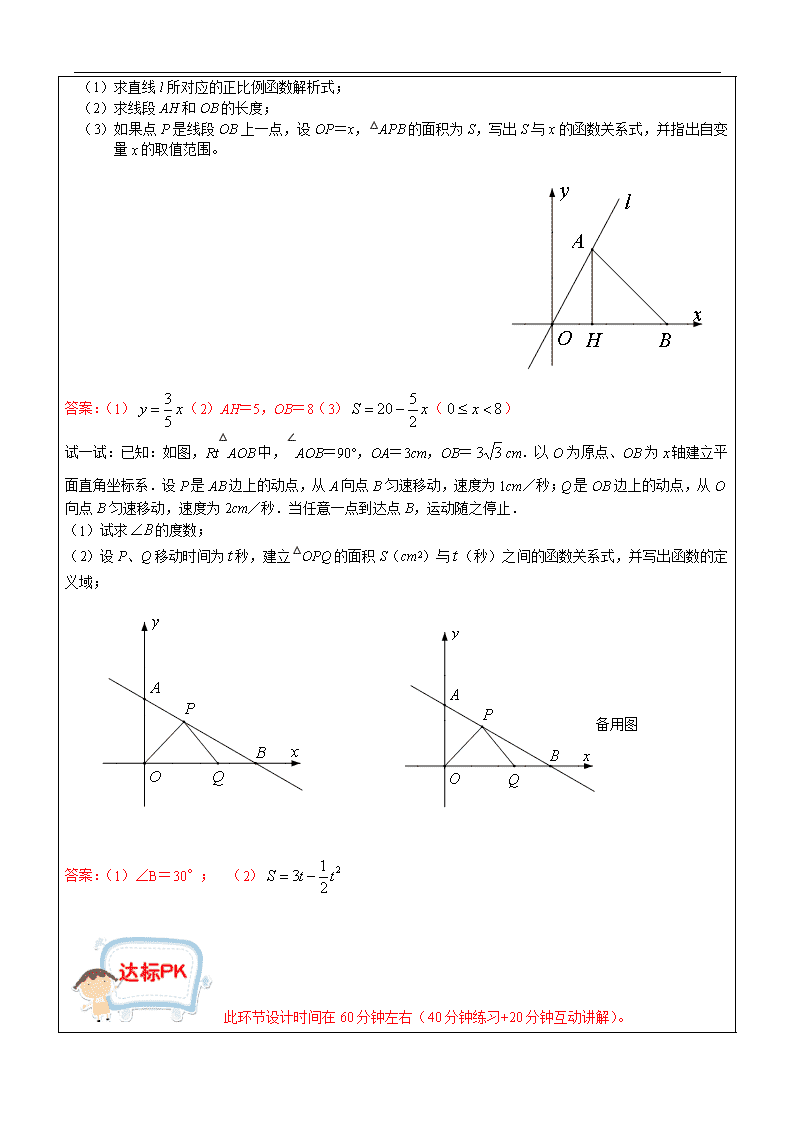
辅导教案 学员姓名： 学科教师：‎ 年 级： 辅导科目： ‎ 授课日期 ‎××年××月××日 时 间 A / B / C / D / E / F段 主 题 阶段性复习与检测 教学内容 ‎1．巩固复习八年级第一学期的二次根式、一元二次方程、正反比例函数、几何证明章节知识。‎ ‎（此环节设计时间在10-15分钟）‎ 说明：学科教师根据八年级上学期的章节思维导图，通过提问的方式与学生一起回顾相关知识点，也可以通过三人之间的竞争抢答来加强对知识点的巩固，让学生与学生之间多一些互动。‎ ‎（此环节设计时间在20-30分钟）‎ 例题1：如图，正比例函数图像直线l经过点A（3，5），点B在x轴的正半轴上，且∠ABO＝45°，AH⊥OB，垂足为点H。‎ ‎　（1）求直线l所对应的正比例函数解析式； ‎ ‎　（2）求线段AH和OB的长度； ‎ ‎　（3）如果点P是线段OB上一点，设OP＝x，△APB的面积为S，写出S与x的函数关系式，并指出自变量x的取值范围。‎ 答案：（1）（2）AH＝5，OB＝8（3）（）‎ 试一试：已知：如图，Rt△AOB中，∠AOB＝90°，OA＝‎3cm，OB＝cm．以O为原点、OB为轴建立平面直角坐标系．设P是AB边上的动点，从A向点B匀速移动，速度为‎1cm／秒；Q是OB边上的动点，从O向点B匀速移动，速度为‎2cm／秒．当任意一点到达点B，运动随之停止．‎ ‎（1）试求的度数；‎ ‎（2）设P、Q移动时间为秒，建立△OPQ的面积S（cm2）与（秒）之间的函数关系式，并写出函数的定义域；‎ ‎ ‎ 答案：（1）∠B＝30°； （2）‎ 此环节设计时间在60分钟左右（40分钟练习+20分钟互动讲解）。‎ 一、填空题（本大题共10题，每题3分，满分30分）‎ ‎1．化简二次根式＝ ．‎ ‎2．在实数范围内因式分解：______________________．‎ ‎3．方程的解是_________________．‎ ‎4．如果反比例函数的图像在当的范围内，随着的增大而增大，那么的取值范围 是__________．‎ ‎5．如果关于x的一元二次方程（c是常数）没有实数根，那么c的取值范围是__ ____．‎ ‎6．若直角三角形两直角边的长是8和6，则斜边上的高是_______ ___．‎ ‎7．点C在x轴上，点C到点A（﹣1，4）与点B（2，﹣5）的距离相等，则点C的坐标为 ．‎ ‎8．如图，等腰三角形ABC中，已知，AB的垂直平分线交AC于D，那么的度数 为 ．‎ ‎9．如图，∠AOE＝∠BOE＝15°，EF∥OB，EC⊥OB，若EC＝1，那么EF＝　_________　.‎ D A B C 第8题图 ‎10．如图，是的中线，，，把沿对折，使点落在的位置，那么 cm．‎ 二、选择题（本大题共4题，每题4分，满分16分）‎ ‎11．下列关于x的方程一定有实数解的是（　 　　）‎ A． B． C． D．‎ ‎12．下列命题中，不正确的是（　 　　）‎ ‎（A）各有一个角为95°，且底边相等的两个等腰三角形全等； ‎ ‎（B）各有一个角为40°，且底边相等的两个等腰三角形全等；‎ ‎（C）各有一个角为40°，且其所对的直角边相等的两个直角三角形全等；‎ ‎（D）各有一个角为40°，且有斜边相等的两个直角三角形全等． ‎ ‎13．在Rt△中，，，AC＝2，如果将这个三角形折叠，使得点B与点A 重合，折痕交AB于点M，交BC于点N，那么BN等于（ ）．‎ ‎ （A） 2 （B） 4 （C） 6 （D） 8‎ ‎14．已知函数中y随x的增大而增大，那么它和函数在同一直角坐标平面内的大致图像可能是（ ）．‎ x y O x y O x y O x y O ‎ ‎ ‎ ‎ ‎(A) (B) (C) (D)‎ 三、计算题（本大题共3题，第15、16题各6分，第17题8分，满分20分）‎ ‎15．用配方法解方程：‎ ‎16．计算： ‎ ‎17．已知函数，与x成反比例，与成正比例，当时，，当时，。‎ ‎　（1）求y关于x的函数的解析式；‎ ‎　（2）求当时的函数值。‎ 四、综合题（本大题共3题，第18题10分，第19题、20题各12分，满分34分）‎ ‎0‎ ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎60‎ t（分钟）‎ s（千米）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 第18题图 ‎18．甲、乙两人同时从A地前往相距‎5千米的B地．甲骑自行车，途中修车耽误了20分钟，甲行驶的路程s（千米）关于时间t（分钟）的函数图像如图所示；乙慢跑所行的路程s（千米）关于时间t（分钟）的函数解析式为．‎ ‎（1）在图中画出乙慢跑所行的路程关于时间的函数图像；‎ ‎（2）乙慢跑的速度是每分钟 千米；‎ ‎（3）甲修车后行驶的速度是每分钟 千米；‎ ‎（4）甲、乙两人在出发后，中途 分钟时相遇．‎ ‎19．如图，在中，点P为BC边中点，直线a绕顶点A旋转，若B、P在直线a的两侧，直线a于点M，直线a于点N，联结PM、PN， 延长MP交CN于点E．‎ ‎（1）求证：≌； （2）求证：．‎ A B M P N E C a ‎20．已知：在△ABC中，∠ABC＝90°，点E在射线BA上,，ED与直线AC垂直， 垂足为D，且点M为EC中点， 联结BM， DM.‎ ‎（1）如图1，若点E在线段AB上，探究线段BM与DM及∠BMD与∠BCD所满足的数量关系，并直接写出你得到的结论；‎ ‎（2）如图2，若点E在BA延长线上，你在（1）中得到的结论是否发生变化？写出你的猜想并加以证明.‎ ‎ ‎ 解：（1）BM与DM的数量关系是： ；‎ ‎∠BMD与∠BCD所满足的数量关系是： .‎ ‎（2）‎ 参考答案：‎ 一、填空题：‎ ‎1、； 2、； 3、； 4、； 5、； 6、；‎ ‎7、； 8、30°； 9、2； 10、‎ 二、选择题：‎ ‎11、B； 12、B； 13、B； 14、D 三、计算题：‎ ‎15、； 16、； 17、（1） （2）﹣21‎ 四．解答题：‎ ‎18、（1）略； （2）； （3）； （4）24； 19、证明略；‎ ‎20、解：（1） 结论：BM＝DM，∠BMD＝2∠BCD. ‎ ‎（2）在（1）中得到的结论仍然成立. 即BM＝DM，∠BMD＝2∠BCD.‎ ‎∵ 点M是Rt△BEC的斜边EC的中点（已知），‎ ‎∴ BM＝EC＝MC（直角三角形斜边上的中线等于斜边的一半）. ‎ 同理，DM＝EC＝MC. ∴ BM＝DM. ‎ ‎∵ BM＝ MC，DM ＝MC（已证），‎ ‎∴ ∠CBM ＝∠BCM， ∠DCM＝∠CDM. ‎ ‎∴ ∠BMD＝∠EMB—∠EMD＝2∠BCM—2∠DCM ‎＝2(∠BCM-∠DCM)＝ 2∠BCD. ‎ 即 ∠BMD＝2∠BCD. ‎ 补充类试题：（可选择使用）‎ ‎1．已知，如图，在△ABC中，∠C＝90°，AC＝BC＝4，点M是边AC上一动点（与点A、C不重合），点N在边CB的延长线上，且AM＝BN，联结MN交边AB于点P．‎ ‎（1）猜测MP与NP的数量关系；‎ ‎（2）若设AM＝x，BP＝y，求y与x之间的函数关系式，并写出它的定义域；‎ ‎ ‎ 答案：（1）证明：过点M作MD∥BC 交AB于点D．‎ ‎∵MD∥BC，∴∠MDP＝∠NBP．‎ ‎∵AC＝BC，∠C＝90°∴∠A＝∠ABC＝45°．‎ ‎∵MD∥BC，∴∠ADM＝∠ABC＝45°．‎ ‎∴∠ADM＝∠A，∴AM＝DM．‎ ‎∵AM＝BN，∴BN＝DM．‎ 在△MDP和△NBP中，∠MDP＝∠NBP，∠MPD＝∠NPB，BN＝DM ‎∴△MDP≌△NBP． ∴MP＝NP．‎ ‎（2）在Rt△ABC中，∵∠C＝90°，AC＝BC＝4，∴．‎ ‎∵MD∥BC，∴∠AMD＝∠C＝90°．‎ 在Rt△ADM中，AM＝DM＝x，∴．‎ ‎∵△MDP≌△NBP，∴DP＝BP＝y．‎ ‎∵AD+DP+PB＝AB，∴．‎ ‎∴所求的函数解析式为：． 定义域为：． ‎ ‎2．已知，如图，在Rt△ABC中，∠A＝90°，AB＝AC＝1，P是AB边上不与A点、B点重合的任意一个动点，PQ⊥BC于点Q，QR⊥AC于点R。‎ ‎（1）求证：PQ＝BQ；‎ ‎（2）设BP＝x，CR＝y，求y关于x的函数解析式，并写出定义域；‎ ‎（3）当x为何值时，PR//BC。‎ 答案：（1）证明略； （2）； （3）‎ ‎（此环节设计时间在5-10分钟内）‎ 让学生回顾本节课所学的重点知识，以学生自我总结为主，学科教师引导为辅，为本次课做一个总结回顾 对错题进行整理：‎ ‎1．在Rt△ABC中，∠C＝90°，AC＝6，点D是斜边AB中点，作DE⊥AB，交直线AC于点E．‎ ‎（1）若∠A＝30°，求线段CE的长；‎ ‎（2）当点E在线段AC上时，设BC＝x，CE＝y，求y关于x的函数解析式，并写出定义域；‎ ‎（3）若CE＝1，求BC的长．‎ ‎ ‎ 解：（1）联结BE，点D是AB中点且DE⊥AB， ∵∠A＝30°， ∴∠ABC＝90°-30°＝60°， 又∵DE垂直平分AB， ∴∠ABE＝∠BAE＝30°，∠CBE＝∠ABC-∠ABE＝30°， 又∵∠C＝90°，∴CE＝BE＝AE， ∵AC＝6，∴BE＝AE＝4，CE＝BE＝2 （2）依题意：AE＝BE＝6-y， 在Rt△BCE中，由勾股定理得BC2+CE2＝BE2，即x2+y2＝（6-y）2， ∴（0＜x≤6）‎ ‎（3）当点E在线段AC上时，由（2）得，解得（负值舍） 当点E在AC延长线上时，AE＝BE＝7， 在Rt△BCE中，由勾股定理得BC2+CE2＝BE2，即x2+12＝72．解得（负值舍）． 综上所述，满足条件的BC的长为或 预习思考：‎ ‎1．复习回顾用“描点法”画一个正反比例函数的图像的一般步骤是什么？‎ ‎2．用“描点法”分别画出函数y＝3x+1的图像；‎ x ‎…‎ ‎－3‎ ‎－2‎ ‎－1‎ ‎0‎ ‎1‎ ‎2‎ ‎…‎ y