2020八年级数学上册 单元清五 （新版）浙教版 6页

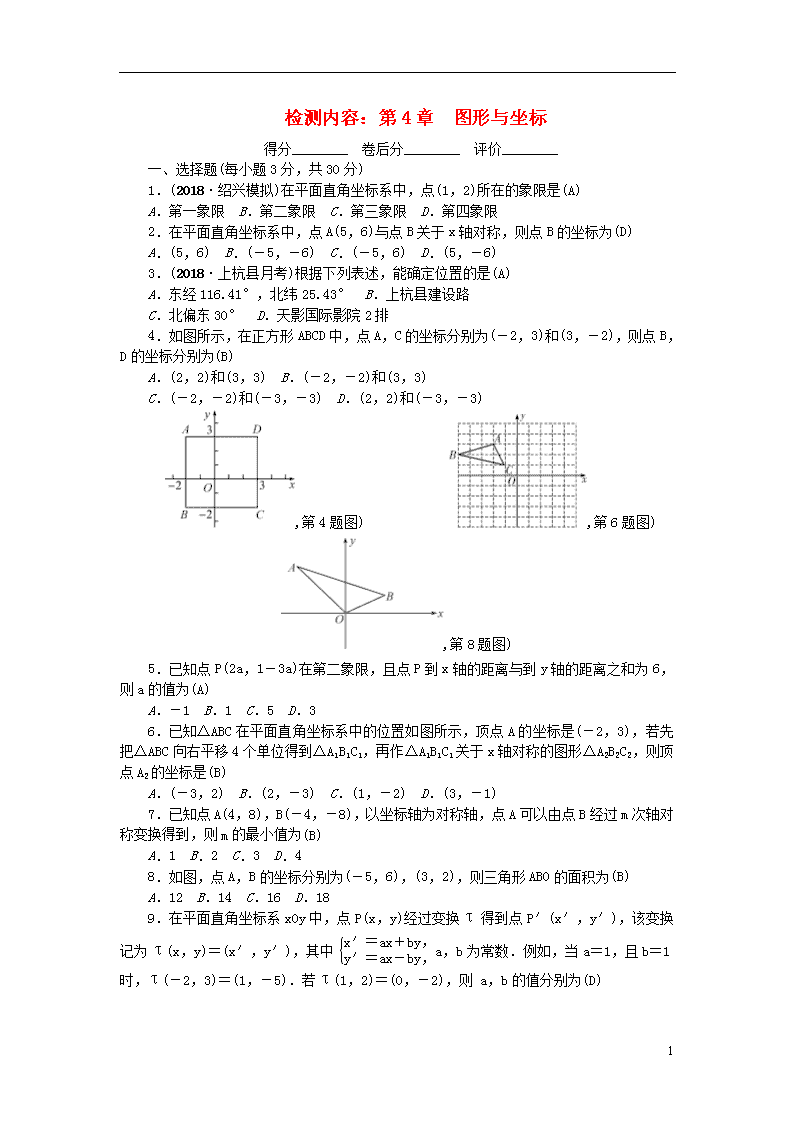
检测内容：第4章　图形与坐标 得分________　卷后分________　评价________‎ 一、选择题(每小题3分，共30分)‎ ‎1．(2018·绍兴模拟)在平面直角坐标系中，点(1，2)所在的象限是(A)‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎2．在平面直角坐标系中，点A(5，6)与点B关于x轴对称，则点B的坐标为(D)‎ A．(5，6) B．(－5，－6) C．(－5，6) D．(5，－6)‎ ‎3．(2018·上杭县月考)根据下列表述，能确定位置的是(A)‎ A．东经116.41°，北纬25.43° B．上杭县建设路 C．北偏东30° D．天影国际影院2排 ‎4．如图所示，在正方形ABCD中，点A，C的坐标分别为(－2，3)和(3，－2)，则点B，D的坐标分别为(B)‎ A．(2，2)和(3，3) B．(－2，－2)和(3，3)‎ C．(－2，－2)和(－3，－3) D．(2，2)和(－3，－3)‎ ‎,第4题图)　　　　　　,第6题图)　　　　,第8题图)‎ ‎5．已知点P(‎2a，1－‎3a)在第二象限，且点P到x轴的距离与到y轴的距离之和为6，则a的值为(A)‎ A．－1 B．‎1 C．5 D．3‎ ‎6．已知△ABC在平面直角坐标系中的位置如图所示，顶点A的坐标是(－2，3)，若先把△ABC向右平移4个单位得到△A1B‎1C1，再作△A1B‎1C1关于x轴对称的图形△A2B‎2C2，则顶点A2的坐标是(B)‎ A．(－3，2) B．(2，－3) C．(1，－2) D．(3，－1)‎ ‎7．已知点A(4，8)，B(－4，－8)，以坐标轴为对称轴，点A可以由点B经过m次轴对称变换得到，则m的最小值为(B)‎ A．1 B．‎2 C．3 D．4‎ ‎8．如图，点A，B的坐标分别为(－5，6)，(3，2)，则三角形ABO的面积为(B)‎ A．12 B．‎14 C．16 D．18‎ ‎9．在平面直角坐标系xOy中，点P(x，y)经过变换τ得到点P′(x′，y′)，该变换记为τ(x，y)＝(x′，y′)，其中a，b为常数．例如，当a＝1，且b＝1时，τ(－2，3)＝(1，－5)．若τ(1，2)＝(0，－2)，则 a，b的值分别为(D)‎ 6‎ A. －1，－ B. 1, C. 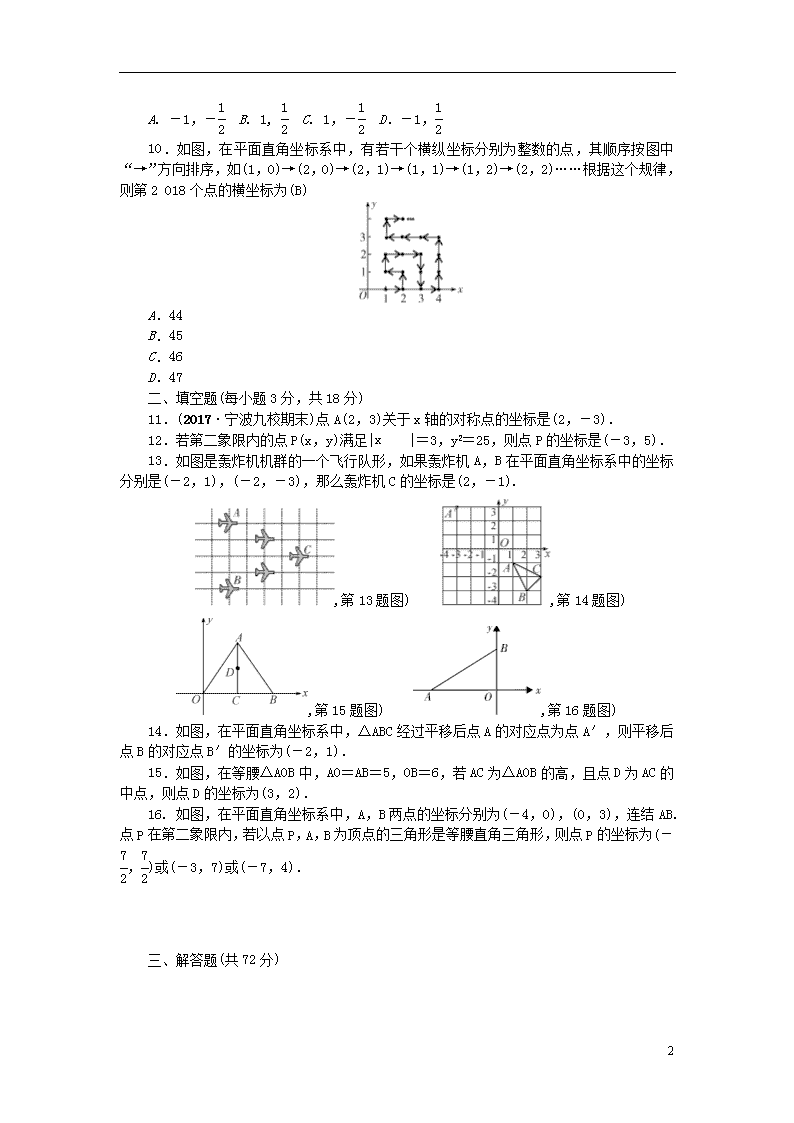1，－ D．－1， ‎10．如图，在平面直角坐标系中，有若干个横纵坐标分别为整数的点，其顺序按图中“→”方向排序，如(1，0)→(2，0)→(2，1)→(1，1)→(1，2)→(2，2)……根据这个规律，则第2 018个点的横坐标为(B)‎ A．44‎ B．45‎ C．46‎ D．47‎ 二、填空题(每小题3分，共18分)‎ ‎11．(2017·宁波九校期末)点A(2，3)关于x轴的对称点的坐标是(2，－3)．‎ ‎12．若第二象限内的点P(x，y)满足＝3，y2＝25，则点P的坐标是(－3，5)．‎ ‎13．如图是轰炸机机群的一个飞行队形，如果轰炸机A，B在平面直角坐标系中的坐标分别是(－2，1)，(－2，－3)，那么轰炸机C的坐标是(2，－1). ‎ ‎,第13题图)　　,第14题图)　　,第15题图)　　,第16题图)‎ ‎14．如图，在平面直角坐标系中，△ABC经过平移后点A的对应点为点A′，则平移后点B的对应点B′的坐标为(－2，1)．‎ ‎15．如图，在等腰△AOB中，AO＝AB＝5，OB＝6，若AC为△AOB的高，且点D为AC的中点，则点D的坐标为(3，2)．‎ ‎16. 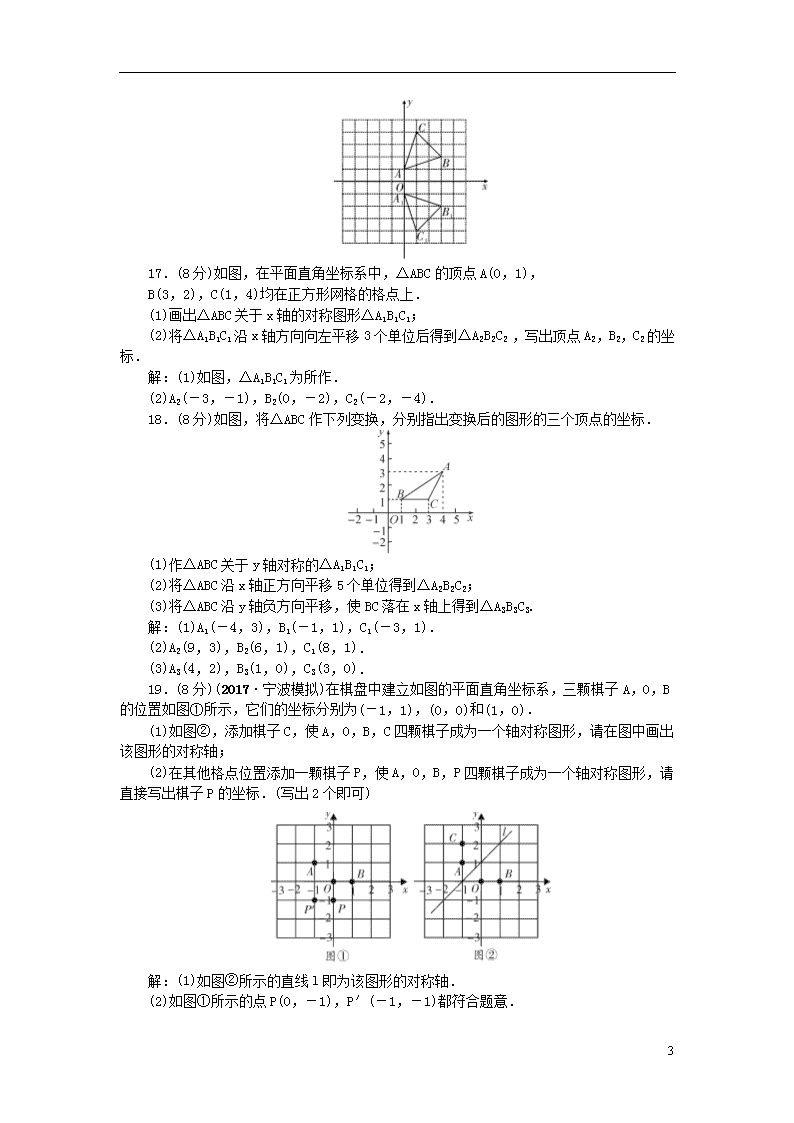如图，在平面直角坐标系中，A，B两点的坐标分别为(－4，0)，(0，3)，连结AB.点P在第二象限内，若以点P，A，B为顶点的三角形是等腰直角三角形，则点P的坐标为(－，)或(－3，7)或(－7，4)．‎ 三、解答题(共72分)‎ 6‎ ‎17．(8分)如图，在平面直角坐标系中，△ABC的顶点A(0，1)，‎ B(3，2)，C(1，4)均在正方形网格的格点上．‎ ‎(1)画出△ABC关于x轴的对称图形△A1B‎1C1；‎ ‎(2)将△A1B‎1C1沿x轴方向向左平移3个单位后得到△A2B‎2C2 ，写出顶点A2，B2，C2的坐标．‎ 解：(1)如图，△A1B1C1为所作．‎ ‎(2)A2(－3，－1)，B2(0，－2)，C2(－2，－4)．　‎ ‎18．(8分)如图，将△ABC作下列变换，分别指出变换后的图形的三个顶点的坐标．‎ ‎(1)作△ABC关于y轴对称的△A1B‎1C1；‎ ‎(2)将△ABC沿x轴正方向平移5个单位得到△A2B‎2C2；‎ ‎(3)将△ABC沿y轴负方向平移，使BC落在x轴上得到△A3B‎3C3.‎ 解：(1)A1(－4，3)，B1(－1，1)，C1(－3，1)．‎ ‎(2)A2(9，3)，B2(6，1)，C1(8，1)．‎ ‎(3)A3(4，2)，B3(1，0)，C3(3，0)．‎ ‎19．(8分)(2017·宁波模拟)在棋盘中建立如图的平面直角坐标系，三颗棋子A，O，B的位置如图①所示，它们的坐标分别为(－1，1)，(0，0)和(1，0)．‎ ‎(1)如图②，添加棋子C，使A，O，B，C四颗棋子成为一个轴对称图形，请在图中画出该图形的对称轴；‎ ‎(2)在其他格点位置添加一颗棋子P，使A，O，B，P四颗棋子成为一个轴对称图形，请直接写出棋子P的坐标．(写出2个即可)‎ 解：(1)如图②所示的直线l即为该图形的对称轴．‎ ‎(2)如图①所示的点P(0，－1)，P′(－1，－1)都符合题意．‎ 6‎ ‎20．(8分)如图，点A(3，1)表示放置3个胡萝卜，1棵青菜，点B(2，3)表示放置2个胡萝卜，3棵青菜．‎ ‎(1)请你写出点C，D，E，F所表示的意义；‎ ‎(2)若一只兔子从点A到达点B(顺着方格线走)，有以下几条路线可以选择：①A→C→D→B；②A→F→D→B；③A→F→E→B.请你帮可爱的兔子选一条路，使它得到的食物最多．‎ 解：(1)点C(2，1)表示放置2个胡萝卜，1棵青菜；点D(2，2)表示放置2个胡萝卜，2棵青菜；点E(3，3)表示放置3个胡萝卜，3棵青菜；点F(3，2)表示放置3个胡萝卜，2棵青菜．‎ ‎(2)走路线①可以得到9个胡萝卜，7棵青菜；走路线②可以得到10个胡萝卜，8棵青菜；走路线③可以得到11个胡萝卜，9棵青菜．故小白兔走路线③得到的食物最多．‎ ‎21．(8分)如图，四边形ABCD各顶点的坐标分别为A(0，0)，B(9，0)，C(7，5)，D(2，7)，求四边形ABCD的面积．‎ 解：四边形ABCD的面积为42.‎ ‎22．(10分)已知等腰直角三角形ABC的直角顶点C在x轴上，斜边AB在y轴上，点A在点B的上方，直角边AC＝2，试写出顶点A，B，C的坐标．‎ 解：当直角顶点C在x轴正半轴上时，如图①.由△ABC是等腰直角三角形，易得△AOC，△BOC为等腰直角三角形．∴AO2＋OC2＝AC2，∴AO＝OC＝.∴A(0，)，B(0，－)，C(，0)．当直角顶点C在x轴负半轴上时，如图②，同理可得，A(0，)，B(0，－)，C(－，0)‎ 6‎ ‎23．(10分)在平面直角坐标系xOy中，对于任意两点P1(x1，y1)与P2(x2，y2)的“识别距离”，给出如下定义：‎ 若|x1－x2|≥|y1－y2|，则点P1(x1，y1)与点P2(x2，y2)的“识别距离”为|x1－x2|；‎ 若|x1－x2|＜|y1－y2|，则点P1(x1，y1)与点P2(x2，y2)的“识别距离”为|y1－y2|.‎ ‎(1)已知点A(－1，0)，点B为y轴上一动点．‎ ‎①若点A与点B的“识别距离”为2，请写出满足条件的点B的坐标；‎ ‎②直接写出点A与点B的“识别距离”的最小值；‎ ‎(2)已知点C的坐标为(m，m＋3)，点D的坐标为(0，1)，求点C与点D的“识别距离”的最小值及相应的点C的坐标．‎ 解：(1)设点B的坐标为点(0，m)．当－1≤m≤1时，点A与点B的“识别距离”为1；当m＜－1或m＞1时，点A与点B的“识别距离”为.①由题意，得＝2，m＜－1或m＞1，∴m＝±2，∴点B的坐标为(0，2)或(0，－2)．‎ ‎②点A与点B的“识别距离”的最小值为1.‎ ‎(2)由题意，得当m≤－或m≥8时，点C与点D的“识别距离”为，易得≥ ，∴点C与点D的“识别距离”的最小值为；当－＜m＜8时，点C与点D的“识别距离”为，易得＜＜8.综上所述，点C与点D的“识别距离”的最小值为，相应的点C的坐标为(－，)．‎ ‎24．(12分)如图，在平面直角坐标系中，已知点A(a，0)，B(b，0)，其中a，b满足|a＋1|＋(b－3)2＝0.‎ ‎(1)填空：a＝－1，b＝3；‎ ‎(2)若在第三象限内有一点M(－2，m)，请用含m的式子表示△ABM的面积；‎ ‎(3)在(2)的条件下，当m＝－时，在y轴上是否存在一点P，使得△BMP的面积等于△ABM的面积的？若存在，请求出点P的坐标；若不存在，请说明理由．‎ 解：(2)过点M作MN⊥x轴于点N，∵A(－1，0)，B(3，0)，∴AB＝1＋3＝4.∵点M(－2，m)在第三象限，∴MN＝|m|＝－m，∴S△ABM＝AB·MN＝×4×(－m)＝－2m.‎ 6‎ ‎(3)存在，理由如下：当m＝－时，由(1)得S△ABM＝－2×(－)＝3.设点P的坐标为(0，k)．‎ ‎①当点P在y轴的正半轴上，即k＞0时．易得S△BMP＝5×(＋k)－×2×(＋k)－×5×－×3×k＝k＋，∵S△BMP＝S△ABM，∴k＋＝×3，解得k＝，∴此时点P的坐标为(0，)；‎ ‎②当点P与原点重合，即k＝0时，易得S△BMP＝×3×＝≠S△ABM，∴不符合题意；‎ ‎③当点P在y轴的负半轴上，即k＜0时．易得S△BMP＝－5k－×2×(－k－)－×5×－×3×(－k)＝－k－.∵S△BMP＝S△ABM，即－k－＝×3，解得k＝－.∴此时点P的坐标为(0，－)．‎ 综上所述，在y轴上存在点P(0，)或(0，－)，使得△BMP的面积等于△ABM的面积的.‎ 6‎